考虑气体悬浮的关井井筒压力计算方法
2021-11-11段文广孙宝江潘少伟王志远
段文广, 孙宝江, 潘 登, 潘少伟, 王志远, 郭 兵, 仉 志
(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.中国石油集团西部钻探工程有限公司, 新疆克拉玛依 830011;3.大港油田对外合作项目部,天津300457)
井筒压力计算方法一般建立在气-牛顿流体两相流动模型基础上[1-9],鲜有考虑钻井液非牛顿流体特性对井筒压力的影响。石油钻探中使用的钻井液具有屈服应力[10],用以保证钻井液停止循环时环空中岩屑不在密度差作用下下沉。屈服应力的存在也将导致侵入井筒内的气体不能在密度差作用下上升,使气体悬浮在钻井液中[11-13]。忽略钻井液中气体悬浮现象将导致气侵关井后井筒压力计算结果不准确[12,14]。Nunes等[15]建立了深水井涌解析模型。孙宝江等[1]考虑井筒与油藏连续耦合的条件、油气间相变、井筒周围多温度梯度环境和天然气水合物相变等因素,将井筒内流体分为7种不同组分,建立了七组分井筒多相流控制方程。任美鹏等[7]考虑关井期间井筒续流和气体滑脱综合影响,建立关井期间井筒压力计算模型,并在此基础上给出了气侵关井井筒压力读取方法。尹邦堂等[8]针对新疆克拉2气田高温高压气井关井压力恢复异常现象,综合考虑井筒续流、井筒温度及井筒流体参数的变化特征,基于井筒压力恢复原理,建立了关井期间的井底压力计算模型。孙士慧等[9]考虑井筒储集效应,建立了关井期间井底压力和井口压力的计算模型。但钻井液屈服应力对井筒多相流动和井筒压力计算的影响研究还较少[12,14]。侵入井筒中的气体通常以气泡群的形式分散在钻井液中,多个气泡同时悬浮在钻井液中时,气泡群中各气泡周围流体质点所受应力均不足以克服屈服应力而发生流动。数值模拟发现单个悬浮气泡周围存在一个有限大的屈服区域,屈服区域内流体发生塑性屈服,屈服区域外流体发生弹性应变,气泡周围流体应力场沿半径方向逐渐减小[13,16-19]。当多个悬浮气泡之间距离足够小时,气泡周围流体质点耦合应力将超过流体屈服条件并开始流动,导致多个气泡不能同时悬浮。因此多个气泡同时悬浮时,相邻气泡间存在一个临界距离,使得钻井液中悬浮气体存在一个极限体积分数。屈服应力流体中气体悬浮的研究主要集中在单个气泡临界悬浮条件,试验和数值模拟均发现单个气泡临界悬浮条件与流体屈服应力、表面张力和剪切稀释性等相关,并根据数值模拟结果和试验结果提出了单个气泡临界悬浮条件[17-22]。Johnson等[12]对黄原胶溶液中气体悬浮体积分数进行了测量,发现屈服应力为7.2和14.4 Pa的黄原胶溶液中气体悬浮体积分数分别为0.76%和2.47%,并据此给出了气体极限悬浮体积分数随屈服应力变化的关系。笔者通过气体极限悬浮试验测定不同流体屈服应力、气泡尺寸时气体极限悬浮体积分数,建立气体极限悬浮体积分数预测模型,并在此基础上建立气侵关井后考虑气体悬浮的井筒压力计算方法。
1 气体极限悬浮试验
通常用无量纲数Bi描述屈服应力流体中单个气泡临界悬浮条件:
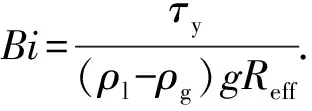
(1)
式中,τy为流体屈服应力,Pa;ρl为液体密度,kg/m3;ρg为气体密度,kg/m3;g为重力加速度,m·s-2;Reff为气泡当量半径,m。
钻井液通常为具有屈服应力的流体,通常用宾汉模型或赫-巴模型来表征其流变性[10]:

(2)
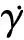
地层压力超过井底压力时,储层中气体将从井底以渗流的形式进入井筒并以小气泡的形式分布在钻井液中。当单个气泡浮力不足以克服屈服应力引起的阻力时,将被束缚在钻井液中,反之则会在浮力作用下上升。多个气泡同时悬浮在钻井液中时,其原理与单气泡悬浮类似,即气泡群浮力不足以克服屈服应力引起的阻力。为获得多气泡同时悬浮时悬浮体积,本文中利用Carbopol溶液模拟钻井液,氮气模拟地层气体,开展气侵后井筒中气体极限悬浮试验。
1.1 试验装置及方法
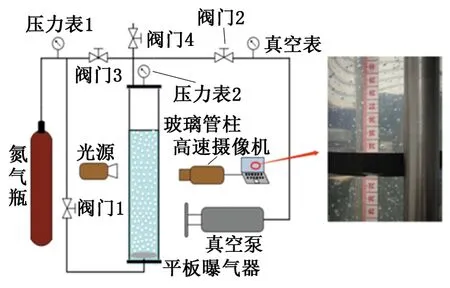
图1 试验装置Fig.1 Experimental device
如图1所示,气体极限悬浮试验装置由模拟井筒模块、气体发生模块、压力控制模块和数据采集模块构成。模拟井筒主要部分为一段高1 200 mm、内径150 mm的有机玻璃,允许最大压力为5 MPa,模拟井筒内置有一段透明刻度尺用于校正气泡尺寸,井筒外部贴有刻度用于确定井筒内液面高度。气体发生模块由氮气瓶、减压阀、气体管线及金属微孔曝气器(平均孔隙直径为10 μm)组成,气体通过底部金属微孔曝气器进入井筒底部。压力控制模块由试验管柱顶部气路、气源及真空组成,用于控制井筒内压力。数据采集模块由高速摄像机以及正对镜头放置于管柱背面的光源组成。
1.2 试验材料及性质
Carbopol溶液透明度高、易清洗且屈服应力值易调至与钻井液接近,试验中用不同质量分数Carbopol溶液模拟钻井液。在去离子水中充分水解后的Carbopol溶液是一种微酸性的不透明溶液,pH值约为3~3.5,且不存在屈服应力。当将溶液pH值在4.6~7.2时,溶液表现出很好的透明性和屈服应力流体性质,其本构方程符合赫-巴模型[11]。试验中将充分水解后的试验溶液用NaOH溶液中和至7,之后利用Physica MCR流变仪对其流变性进行测量。部分试验溶液流变曲线如图2所示。
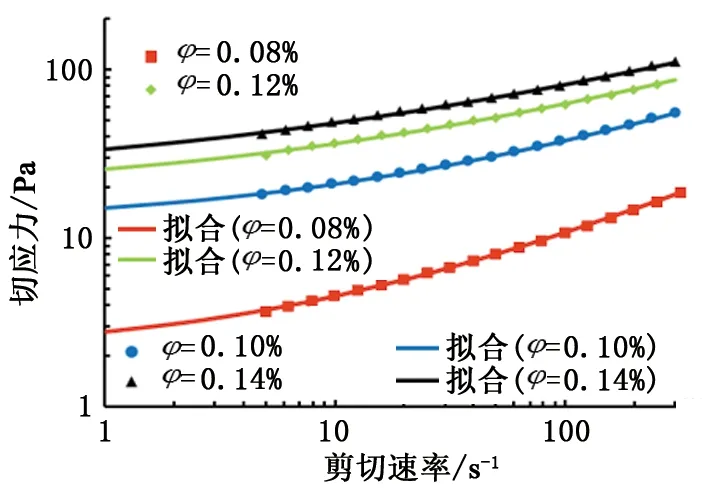
图2 不同体积分数Carbopol溶液流变性及 赫-巴模型拟合Fig.2 Rheological properties of Carbopol solutions with different volume fraction and fitting curves by H-B model
Sun等[13]试验中发现剪切速率较小时,溶液流变性受黏性及弹性影响,剪切速率较大(大于5 s-1)时测量结果与赫-巴模吻合良好。利用赫-巴模型对试验溶液流变曲线进行拟合,其结果如表1所示。
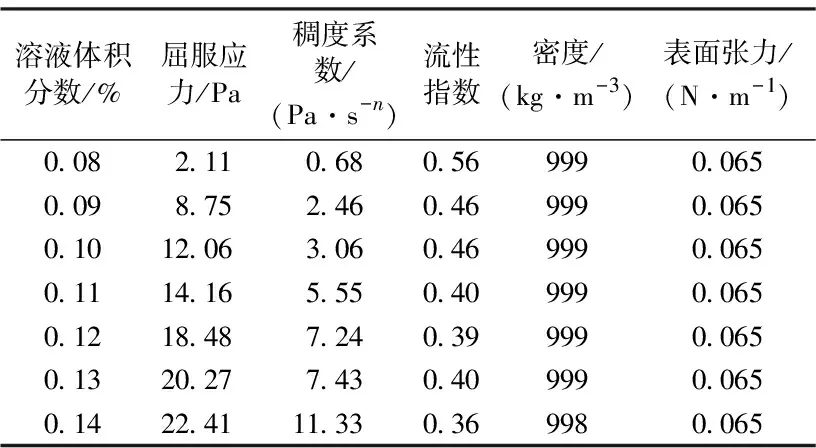
表1 试验溶液性质
1.3 试验数据处理及结果分析
试验中气体悬浮体积分数由管内液面高度确定:
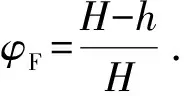
(3)
式中,φF为气体极限悬浮体积分数;H为降压结束后自由液面高度,m;h为加压至5 MPa后液面高度,m。
试验中单个悬浮气泡体积为多个悬浮气泡体积平均体积:
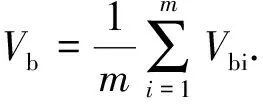
(4)
式中,Vb为气泡平均体积,m3;m为选取照片中悬浮气泡个数;Vbi为编号为i气泡体积,m3。
单个悬浮气泡当量半径为
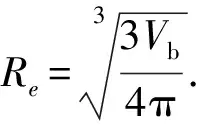
(5)
试验中气体极限体积分数随屈服应力变化规律如图3所示。可以看出,屈服应力为22.41 Pa时悬浮体积分数可达5.57%。但相同屈服应力下不同组试验得到的气体极限悬浮差异较大,如屈服应力为14.16 Pa时,气泡当量半径为1.02和1.37 mm时极限悬浮体积分数分别为3.95%和3.04%。
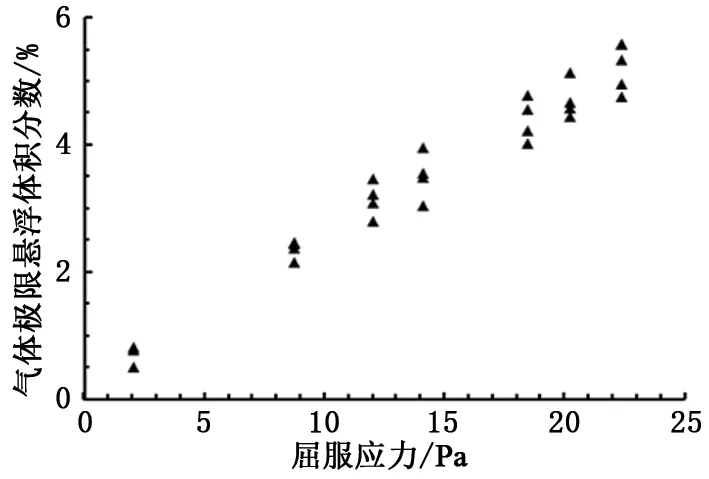
图3 气体极限悬浮体积分数随屈服应力变化Fig.3 Relationship between ultimate gas entrapment volume fraction and yield stress
由图3可知,气泡当量半径也对屈服应力流体中气体极限悬浮体积分数有影响,即气体极限悬浮体积分数影响因素与单气泡临界悬浮条件类似。气体极限悬浮体积分数与表征流体屈服应力及气泡浮力(受当量半径影响)的无量纲数的关系如图4所示。
当气泡群中各气泡不满足单气泡临界悬浮条件时,气泡群中多个气泡也不可能同时悬浮,因此当Bi值小于单气泡临界悬浮条件时,气体极限悬浮体积分数为0。
Tsamopoulos等[17-18]通过数值模拟发现单个气泡Bi大于一个临界值Bic时会悬浮在屈服应力流体中,对于球形气泡Bic约为0.143,随着气泡当量半径增大Bic逐渐增大。Samson等[19,22]在屈服应力为24.1、33.5和40 Pa的Carbopol溶液中进行单气泡悬浮试验,得到的临界悬浮气泡Bic分别0.59、0.72和0.64,约为Tsamopoulos等模拟结果的4倍。Sikorski指出流体弹性也对单气泡临界悬浮时Bic有影响[19]。Sun等[13]建立了一种考虑流体屈服应力、弹性模量、表面张力等因素的悬浮气泡体积预测模型,并开展了单气泡悬浮试验,其模型预测得到的单气泡悬浮Bic与Samson等[19,22]结果吻合较好,由其模型及试验结果得到的球形单气泡悬浮Bic约为0.231。
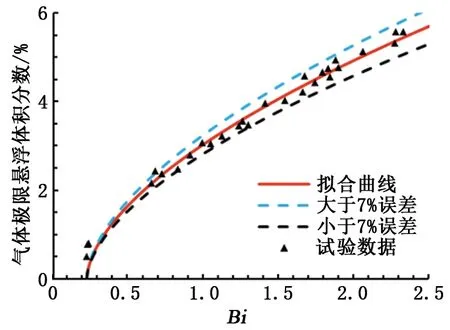
图4 气体极限悬浮体积分数随屈Bi变化Fig.4 Changes of ultimate gas entrapment volume fraction with Bi
试验气泡当量半径为0.88~1.34 mm,气泡形状均为球形,取单气泡临界悬浮Bic为0.231对试验结果进行拟合(图4)。屈服应力值为2.11 Pa溶液中悬浮气泡当量半径与该屈服应力下单个临界悬浮气泡半径几乎相同,该屈服应力下气体极限悬浮体积分数约为0.68%,略于模型预测结果。除该屈服应力下数据外,拟合曲线与试验结果误差小于7%。
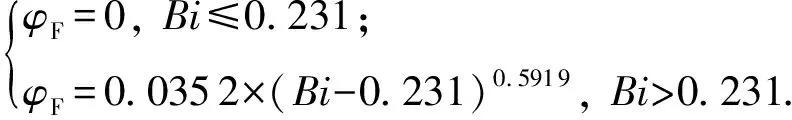
(6)
当流体的屈服应力为0~22.4 Pa且Bi不超过2.5时,本模型适用。
2 关井条件下气体运移模型
钻井过程中发生气侵关井后,准确描述井筒压力变化是确定井控参数的关键[7]。现有关于关井后井筒压力计算的研究主要集中在气体侵入后气体滑脱速度及关井后续流效应等方面[7-9,26-30],Johnson等[12]、Pan等[14]指出侵入井筒内气体可分为悬浮及运移2种状态,气体悬浮量对井筒压力计算具有重要影响。本文中在试验建立气体极限悬浮预测模型的基础上,考虑侵入气体悬浮及运移状态、关井后井筒与地层耦合等因素建立一种考虑气体悬浮的井筒压力计算模型。模型建立过程中作如下假设:
(1)气体前缘位置以下的环空中含气率为气体极限悬浮体积分数;
(2)关井后井筒内温度场分布与环境温度相同,忽略气体上升过程中传热;
(3)不考虑井筒弹性和钻井液压缩性;
(4)不考虑侵入气体溶解度和水合物相变。
2.1 井筒内气体分布及运移特征描述
不考虑井筒弹性及钻井液压缩性时,关井后井筒环空总体积一定,井筒内压力变化与井筒内气体分布形式、气体滑脱速度、关井后地层气体继续侵入和钻井液向地层滤失等因素影响。其中分布形式、滑脱上升速度受钻井液流变性和气泡尺寸影响,气体侵入速度和钻井液滤失速度受井底压力影响。
压差作用下从地层侵入井底的气泡平均当量半径可由经验式描述[23]:
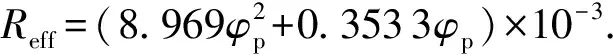
(7)
式中,φp为地层孔隙度,无因次。
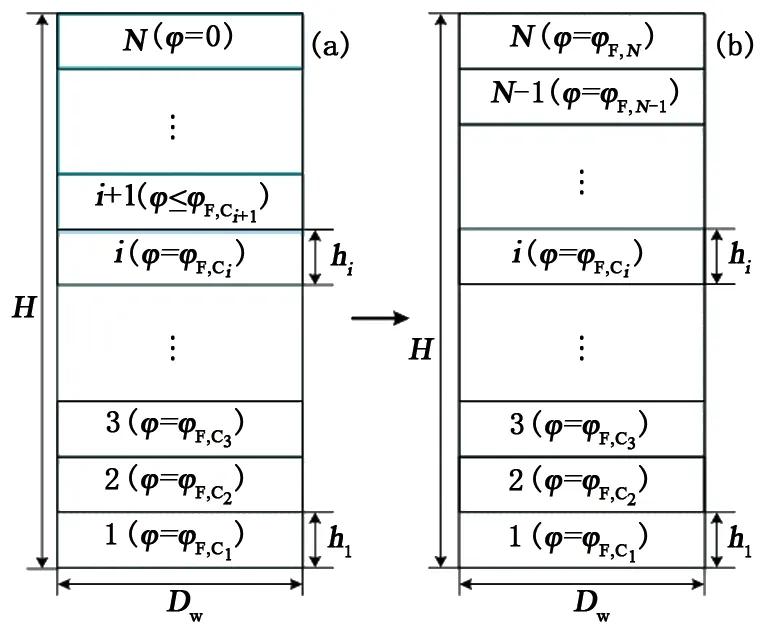
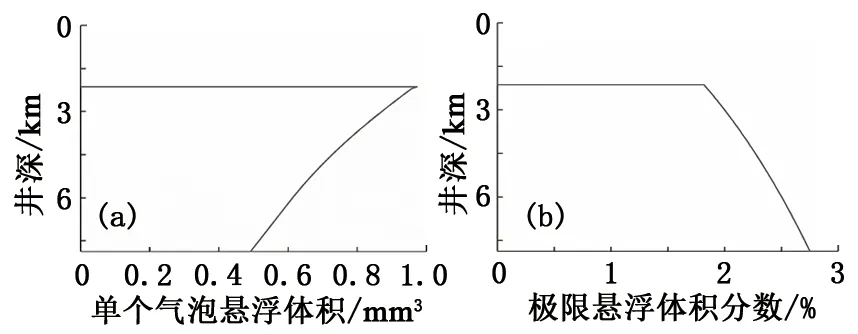
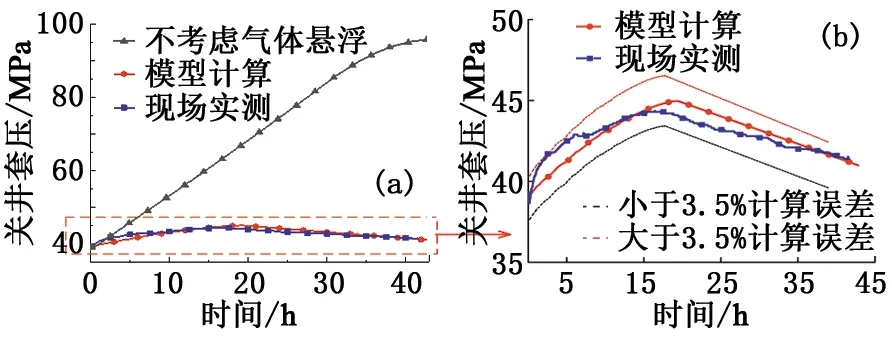
当单个气泡体积和钻井液屈服应力确定后,井筒内各井段中气体极限悬浮体积分数可由式(6)计算。从井底开始,当井段内气体体积达到极限悬浮体积分数后,剩余气体将滑脱上升。对气泡在液体中滑脱速度预测模型的研究[24-28]对气泡屈服应力考虑较少。潘少伟[11]发现在Re<20或Re>50时,Margaritis[26]模型可用于屈服应力流体中气泡运移速度,20 (8) (9) 式中,CD为拖曳力系数;ub为气泡滑脱速度,m/s。 由拖曳力系数定义可得气泡上升速度为 (10) 式中,Vb为气泡体积,m3。 关井后井底压力小于地层压力时,地层气体将在压差作用下持续渗透进入地层,侵入气体体积可由平面径向渗流公式进行计算[14,29]: (11) (12) (13) 式中,Qg(t)为标准状况下气体侵入速度,m3/s;pp为地层压力,Pa;pw(t)为t时刻井底压力,Pa;μg为气体黏度,Pa·s;Z为井筒温度压力条件下气体压缩因子;Pa为标准大气压,Pa;T为井筒温度,K;re为油藏有效半径,m;k为地层渗透率,m2;h为渗流井段高度,m;Za为标准温度压力下气体压缩因子;Ta为标准温度,K;rw为井眼半径,m;ρga为标准状况下气体密度。 随着侵入气体在井筒中上升,井筒压力将不断升高,当井底压力高于地层压力时,钻井液将向地层滤失。钻井液滤失量主要受黏度、地层岩石和流体的压缩性、钻井液的造壁性等影响[30],当钻井液黏度大大超过油气藏流体的黏度时,压裂液滤失主要取决于压裂液的黏度,根据达西方程可得受钻井液黏度控制的滤失系数C1: (14) 式中,C1为受压裂液的黏度控制的滤失系数,m·min-0.5;μm为钻井液黏度,mPa·s。 当钻井液黏度接近于地层流体黏度时,控制钻井液的滤失是地层岩石和流体的压缩性,由于地层岩石和流体受到压缩,会让出一部分空间使得钻井液滤失进去。根据达西渗滤方程,受地层岩石和流体的压缩性控制的滤失系数C2为 (15) 式中,Cf为地层流体的综合压缩系数,MPa-1。 造壁性压裂液的滤失系数C3由试验方法测定: (16) 式中,C3′为试验得到的滤失系数,m·min-0.5;C3为井底压差下滤失系数,m·min-0.5;Δp′为试验压差,Pa。 实际压裂过程中3种机制同时存在。根据分压降公式可得综合滤失系数及钻井液滤失速度分别为 (17) (18) 式中,Ql为钻井液滤失速度,m3/s;t0为井底压力大于地层压力时刻。 为计算关井后井筒中压力变化情况,从井底到井口将井筒划分为N段,如图5所示,图中φ为含气率。侵入气体从井底处开始向上运移,气体前缘位置以下井段单元格内含气率为气体极限悬浮体积分数,任一时刻气体前缘位置高度为非悬浮气泡从关井时刻开始上升的高度。气侵量较小时,当气体到达第i+1个单元格时将全部悬浮,如图5(a)。随着气侵量的增大,当井口处(第N个单元格)含气率也达到极限悬浮体积分数时,井口将开始出现高压气体圈闭,如图5(b)。 图5 气侵后井筒内气体运移及分布状态Fig.5 Gas migration and distribution in wellbore 记关井时侵入井筒内气体总体积为V0,初始井口压力为0,则初始时刻井底压力为 (19) 式中,pw0为初始时刻井底压力,Pa;ρm为钻井液密度,kg·m-3;H为井口到井底深度,m;A0为井底处环空截面积,m2。 侵入井筒内的气体有悬浮和运移2种状态,运移气体前缘位置可由式(8)~(10)计算,气体前缘位置以下井段内单元格中气体悬浮体积分数可由式(6)计算。随着气体上升,井筒内压力逐渐升高,导致各井段内气泡体积及气体悬浮体积分数也发生改变。为求解井筒压力计算,本文中通过有限差分的方法对模型进行求解,主要包括对气体分布的求解和对井口压力的求解。气体分布求解流程如下: (1)记气体到达井段i后井口压力为pt,井段i内气体总体积为φi,t,气泡平均半径为Ri,t; (2)根据井段i内气体气泡平均直径和钻井液屈服应力判断气体是否发生悬浮;若井段i内气体能够悬浮则进入步骤(3),否则进入步骤(4); (3)计算井段i内气体悬浮量,计算井段i以下悬浮气体总量,判断侵入气体是否全部悬浮,若气体全部悬浮则直接进入步骤(7),否则进入步骤(4); (4)计算进入井段i+1内气体量,判断第i+1井段是否为井口段,若第i+1段位为井口段,则进入步骤(7),否则进入步骤(5); (5)计算气体进入第i+1段后井口压力pt+Δt,井段i内气体总体积为φi+1, t+Δt,气泡平均半径为Ri+1, t+Δt; (6)令i=i+1,重复步骤(1)~(5); (7)根据气体全部悬浮或到达井口后各井段内含气率,计算井筒内气体分布。 井筒压力求解步骤如下: (1)记t时刻井口压力为p,井底压力为pw; (2)判断井底压力是否大于地层压力pp,若pw (3)判断钻井液漏失过程中侵入气体是否全部悬浮,若全部悬浮,则进入步骤(6),否则进入步骤(4); (4)判断侵入气体是否到达井口,若侵入气体到达井口则进入步骤(6),否则进入步骤(5); (5)t+Δt时刻井筒压力增量Δp>0,进入步骤(7); (6)t+Δt时刻井筒压力增量Δp<0,进入步骤(7); (7)由t+Δt时刻试算井口压力p+Δp下井筒内气体体积; (8)判断(气体体积+钻井液体积-井筒体积)是否小于设定误差,若不小于,则进入步骤(9),否则进入步骤(10); (9)调整试算压力增量Δp,重复步骤(7)、(8) 使气液相体积之和与井筒体积满足设定误差; (10)得到t+1时刻井口压力p+Δp。 求解过程中空间步长为H/n,时间步长为气体在各单元格上升所需时间。 (20) 式中,ub(i,t)为t时刻单元格i内气体上升速度,m/s。 气体上升至第i个单元格时,记运移气体总体积为Vi,单元格内单个气泡体积为Vbi,井口处压力为pCi。首先判断第i个单元格内单气泡是否满足临界悬浮条件,当单个气泡满足临界悬浮条件时,计算其极限悬浮体积分数φF,Ci。忽略井筒弹性及钻井液压缩性,由气体状态方程可得单元格i内悬浮气体物质的量为 (21) 式中,ng为气体物质的量,mol;Zi为井底处和第i个单元格处气体压缩因子,无量纲;Ti为井底处和第i个单元格处温度,℃;hi、hk分别为第i、k个单元格高度,m;pCi为气体上升至第i个单元格时井口处压力。 当第i个单元格内单个气泡能保持悬浮时,φF,i值为φF,Ci,当单个气泡不能保持悬浮时,φF,i值为0,所有悬浮气体总物质的量为 (22) 进入第i+1个单元格内气体体积、单气泡体积为 (23) (24) 记气体上升至第i个单元格时,任一单元格k内气体实际悬浮体积为Vki,其中k (25) ρmj,i=ρm(1-φF,Cj,i)+ρgj,iφF,Cj,i. (26) 式中,ρmj,i为气体上升至第i个单元格时,第j个单元格内钻井液实际密度,kg/m3;ρgj,i为气体上升至第i个单元格时,第j个单元格内气体实际密度,可由气体状态方程进行计算,kg/m3;φF,Cj,i为气体上升至第i个单元格时,第j个单元格内气体极限悬浮体积分数。 当井筒体积不变且流体不可压缩时,气体上升到第i+1个单元格后,新的井筒压力下气体体积增加量为第i+1个单元格之下悬浮气泡体积减小量与侵入气体体积之差(或与钻井液滤失体积之差)。 由以上公式即可计算得到气体运移至第i+1个单元格时的总体积、单个气泡体积及套压值等参数。从气泡在第1个单元格时开始计算,重复上述步骤,即可得到不同井深处气体悬浮或运移的计算方法。 为验证井筒压力计算模型对气侵关井后井筒压力计算结果准确性,以新疆某实例井为例,对模型进行验证。 新疆阿克苏地区某井钻进至7 874.01 m时发生气侵,总溢流量达到15.12 m3,上提钻具至钻头位置7 862.98 m后关井,关井立压为24.50 MPa,套压为38.6 MPa。关井后套压值增大至约44.3 MPa后逐渐减小,且关井后井口未发现气体。 利用本文中模型对该井气侵后气体分布规律及井筒压力进行计算,得到该井内气体分布规律如图6所示。可以看出,随着井深的减小,井筒压力逐渐降低,井筒内单个悬浮气泡体积也随之增大,对应的气体极限悬浮体积分数由井底处2.75%降低至1.82%。钻井液屈服应力导致侵入井筒中的气体上升至井深2 138 m处后全部悬浮在钻井液中,因此关井后井口未见气体,之后随着钻井液向地层滤失导致井筒压力逐渐降低。 关井后实测井筒压力及计算得到的井筒压力如图7所示。可以看出,不考虑钻井液屈服应力对气体悬浮影响时,随着气体滑脱上升,计算得到井筒压力不断增大,关井42 h后套压升至95.56 MPa,远高于该时刻下实测井筒压力41.4 MPa;考虑气体悬浮及分布规律对井筒压力变化影响时,计算得到的套压值变化规律与实测结果吻合良好。模型计算结果表明关井19.5 h后套压出现峰值44.97 MPa,关井42 h后套压降至约41.13 MPa。实测套压在关井17.5 h后达到峰值44.3 MPa,关井42 h后降至41.4 MPa。与实测结果相比,模型计算得到的套压峰值及关井42 h后套压误差分别为1.51%和0.65%,关井后同一时刻套压误差小于3.5%。模型计算结果与现场实测结果吻合良好,可准确预测气侵关井后井筒压力变化规律。 图6 关井后井筒内气体分布规律Fig.6 Distribution law of invading gas after shut-in 图7 模型计算关井套压变化规律与现场数据对比Fig.7 Comparison between model calculation and field data 通过现场数据对比发现,仅基于气体滑脱上升计算得到的气侵关井后井筒内压力值远高于实测数据,考虑钻井液屈服应力引起的气体悬浮现象能有效提高井筒压力计算精度。 (1)钻井液屈服应力越大、单个悬浮气泡体积越小,井筒中气体极限悬浮体积分数越大。屈服应力为22.41 Pa时,气体极限悬浮体积分数可达5.57%。建立的气体极限悬浮预测模型在屈服应力为0~22.4 Pa时适用,模型预测结果与试验结果相比误差小于7%。 (2)考虑钻井液屈服应力对气体悬浮、运移的影响和井底与地层耦合,建立适用于气侵关井后井筒压力计算的模型及其求解算法。通过求解模型可以得到关井后井筒内气体分布规律和压力变化规律。 (3)侵入气体在钻井液屈服应力阻碍下悬浮在井筒中,导致气侵后井口套压呈现先增大后缓慢减小的变化趋势,且气侵关井后井口处不会出现气体。与现场实测数据对比,套压峰值误差为1.51%,关井后同一时刻套压值误差小于3.5%,模型可用于气侵关井后有气体悬浮时井筒压力精确计算。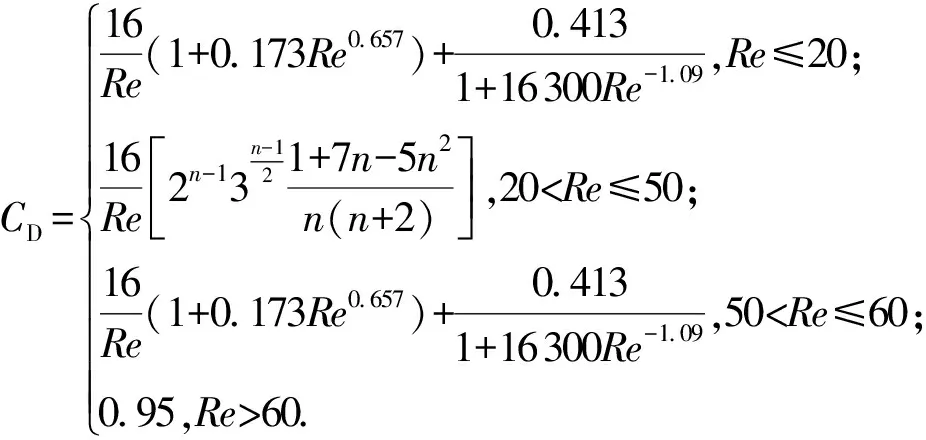
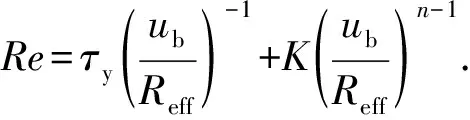
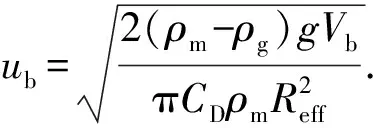
2.2 关井后气体侵入及钻井液滤失描述
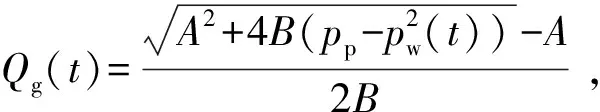
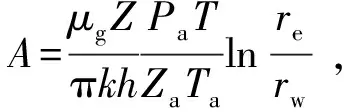
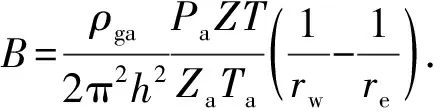
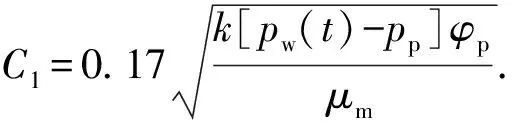
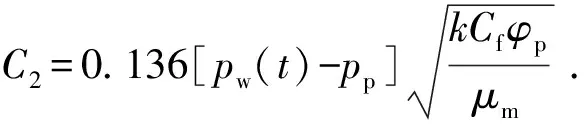
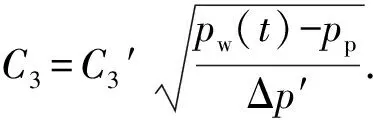
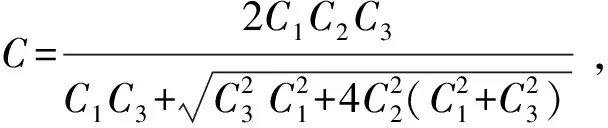
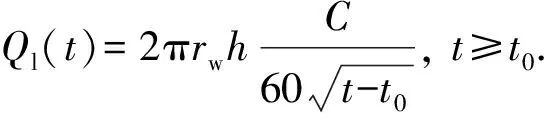
2.3 井筒压力计算模型求解
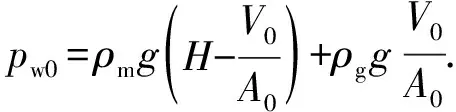
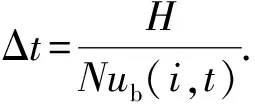
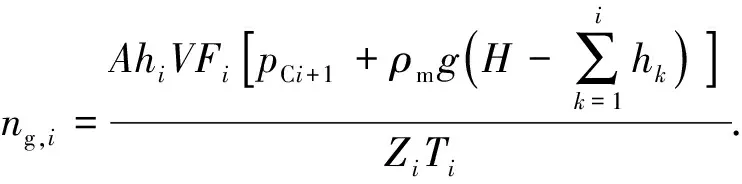
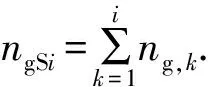
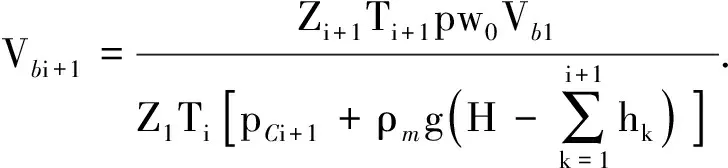
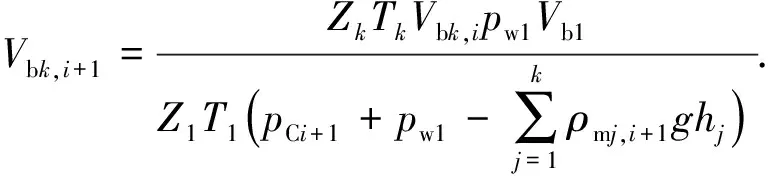
3 模型现场验证
4 结 论
