基于任务分层策略和属性相对变权决策的设备资源优化

王有远，钱伟伟，刘 瑞

(1.南昌航空大学 工业工程研究所，江西 南昌 330063；2.南昌航空大学 航空制造工程学院，江西 南昌 330063)

0 引言

随着云计算、物联网和大数据等技术的发展，智能制造作为一种新型制造模式，已经在制造业中兴起并逐步应用。设备资源作为先进制造技术的物质载体，是企业向智能制造转型升级的重要组成部分，其优化配置水平的提高对于提升企业整体竞争力具有重要意义。

为了解决设备资源等制造资源优化配置问题，近年来国内外学者对其进行了广泛研究。如陈冰等[1]提出了基于非合作博弈的制造资源优化配置方法；张相斌等[2]建立了基于资源用量和交易参考价格的制造资源逆优化配置模型；赵道致等[3]提出了基于Pareto最优的制造资源动态优化配置方法；熊永华等[4]建立了以制造效率和资源负载均衡为目标的多目标优化模型，使用改进的粒子群算法进行求解；ZHANG等[5]提出了任务驱动的制造服务主动发现和优化配置方法；苏凯凯等[6]建立了云制造环境下的制造资源优化配置非合作博弈决策模型，采用改进的遗传算法进行求解；AKBARIPOUR等[7]提出了混合整数规划的资源配置模型；刘晓阳等[8]提出了基于多色集合理论递阶系统的制造资源优化配置方法；TAVANA等[9]提出了基于成组技术的离散布谷鸟优化算法，求解资源分配问题；WANG等[10]提出了基于改进的分布式遗传算法的制造资源优化选择策略。

上述研究主要是将与制造任务相关的成本和负载等作为目标建立优化模型，未考虑任务功能需求的差异性和复杂性；另外，在决策方法方面，多采用多属性固权决策方法，未考虑需求方在属性上的偏好依赖关联行为，存在一定的缺陷。基于以上分析，本文分两步完成智能制造环境下的设备资源优化：①通过分析任务的不同功能需求，提出智能制造环境下设备资源双层优化模型，并设计相应的求解算法，获取候选方案集合；②通过研究需求方在属性上的偏好依赖关联行为，提出基于属性相对变权决策的优选模型；基于该模型从候选方案集合中选取综合评价最高的方案，该方案不但综合评价最优，而且与需求方关于属性偏好依赖关联行为及客观事实高度相符。

1 设备资源双层优化模型

1.1 设备资源优化选择问题描述

设备资源的选择和分配是企业实行智能制造中完成资源服务化管理中的一项关键技术，本文研究的设备资源是指企业生产中涉及的各类加工设备。设备资源组合服务单元是指由不同类型的加工设备通过合理布置而形成的具有独立完成特定加工任务，并经服务化封装注册于企业资源管理平台中的服务输出单元。设备资源优化配置问题的本质是由加工任务(简称任务)需求所驱动，通过选取最佳设备资源组合服务单元(简称设备单元)以实现任务完成的最优化。由于任务需求和设备资源状态都具有动态多变性，为便于模型描述，使得研究更具严谨性和可操作性，本文基于以下假设进行研究：

(1)所提交的任务皆满足设备单元工艺要求。

(2)单个设备单元可以完成多个任务，但同一时间只能执行一个任务。

(3)任务可以在多个设备单元上被执行，但只能从候选设备单元集中进行选取。

(4)具有约束关系的任务，只有在完成前置任务的所有操作之后，才能执行后续任务。

(5)所有任务一旦开始执行，就不能中断。

通常情况下，提交到企业的任务非常复杂，需要调用多个设备单元协同完成，以动态完成复杂任务，其选择映射关系如图1所示。

1.2 设备资源上层优化模型

由于设备资源优化配置通常面对的是具有复杂约束的任务，且约束关系随着任务种类的不同而存在差异，因此用式(1)来描述企业设备单元与任务之间的关系：

(1)

式中QSij(k)表示第k个企业设备单元对任务i的子任务j的完成能力。由于任务之间的约束关系各异，因此用式(2)来描述不同任务之间的约束关系：

(2)

式中ACjl表示子任务j和子任务l之间的约束关系。每个子任务的完成时间由3个部分组成，即加工时间(Making Time, MT)、设置时间(Setup Time, ST)和传递时间(Transfer Time，TT)[11]。加工时间是指企业设备单元完成加工任务消耗的时间，设置时间是指企业设备单元为处理任务所做的准备时间(包括安装、定位等)，传递时间是指将已完成的任务转移到所选企业设备单元的位置以执行后续操作所用的时间。

若Mij(k)为任务i的子任务j被分配到EUNSk时，企业设备单元单位工作负载的加工时间，则加工时间MTij(k)=Mij(k)×wij，wij表示负载量。用式(3)来描述预测开始时间：

PSTij(k)=

(3)

PSTij(k)表示在EUNSk上，任务i的子任务j的预测开始时间，mn(k)为EUNSk在tij之前执行的任务tmn，STmn(k)ij(k)表示从EUNSk上执行任务tmn到tij的设置时间；FTil(g)表示由EUNSg处理前一个子任务til的完成时间;l∈preij，preij表示子任务tij的前一组子任务，preij={l|l∈ACjl=1}；TTij(k)il(g)表示将EUNSg执行的til任务转移到由EUNSk执行的tij任务的传递时间。若EUNSg和EUNSk属于同一个生产车间，则TTij(k)il(g)=0。

EUNSk和EUNSg遵循式(4)中的约束。

QSil(g)=QSij(k)=QSmn(k)=1。

(4)

约束(4)表示EUNSk和EUNSg必须完成各自的子任务tmn、tij和til。若EUNSk在执行tij之前未执行其他任务，则STmn(k)ij(k)=ST0ij(k)，ST0ij(k)为tij在EUNSk上的初始设置时间。

由于从任务i分解的子任务j的实际制造时间(Actual Manufacturing Time, AMT)取决于所选的EUNSk的实际可用时间。若用ATij(k)表示EUNSk可用于执行当前请求的最早时间，则EUNSk执行任务i的子任务j的实际开始时间和完成时间的计算公式如下：

AMTij(k)=max{PSTij(k),ATij(k)};

(5)

FTij(k)=AMTij(k)+MTij(k)。

(6)

其中AMTij(k)、FTij(k)分别表示EUNSk处理任务i的子任务j的实际开始时间和完成时间。

对于单个任务i的优化目标是使其所有子任务的完成时间最短，建立数学模型如下：

i=1,2,…,ny。

(7)

对于全体任务T′的优化目标是最大限度地降低T′的完成时间，建立数学模型如下：

(8)

s.t.

(9)

FTij(k)≤AMTcd(k),若prijcdk=1;

(10)

(11)

约束(9)表示每个子任务只能分配给一个合格的企业设备单元，约束(10)表示企业设备单元在任何给定时间只能执行单个子任务，Prijcdk=1表示任务i的子任务j在任务c的子任务d之前被安排在EUNSk上；约束(11)表示并非所有企业设备单元都能满足任务请求。

1.3 设备资源下层优化模型

在设备资源优化配置中，除了复杂约束关系的任务外，还存在一些未包含约束关系的任务。因此本节讨论此类任务。

定义1任务匹配度。任务匹配度是衡量企业设备单元对任务适合程度的指标参数，其值越大，越理想。物流水平、负载、软硬件水平等是影响任务匹配度的主要因素[12]，具体描述如下：

(1)物流指标 用Lci′j′描述EUNSi′与任务j′之间的物流关系，若具有物流关系，则Lci′j′=0.5，否则Lci′j′=1。

(2)能力指标 用Abi′j′描述EUNSi′对任务j′的加工能力。Abi′j′的取值用向量a=[0,0.2,0.4,0.6,0.8,1]表示，加工能力越强，取值越大，划分依据为人员职称、执行类似任务的次数等。

(3)装备指标 用Capi′描述EUNSi′的软硬件水平，Capi′的取值用向量c=[3,2,1]表示，装备水平越高，取值越大。

(4)兴趣指标 用Ini′j′描述EUNSi′对任务j′的兴趣程度，Ini′j′的取值用向量d=[1,0.8,0.6,0.4，0.2,0]表示，兴趣程度越高，取值越大。

(5)负载指标 用Loai′表示EUNSi′的负载，

(12)

其中Resi′、Ideli′分别表示EUNSi′的剩余资源和使用资源;WR、WI为系数，满足WR+WI=1。

由于任务匹配度包含多种指标，因此综合考虑各指标的影响，构建任务匹配度模型如下：

(13)

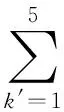
定义2单元协调度。单元协调度是反映各企业设备单元之间协作能力的指标参数[13]，其值越大，越理想。构建单元协调度模型如下：

(14)

式中：si*j*表示执行任务i*的企业设备单元与执行任务j*的企业设备单元之间的协调度，计算方法见文献[13];ns表示T″任务的数量，ns=n-ny;ny表示T′任务的数量。

下层优化模型是在满足时间和成本约束的同时，以任务匹配度和单元协调度最大化为目标。构建下层优化数学模型如下：

(15)

(16)

time≤timez;

(17)

(18)

(19)

其中：xi′j′为0-1逻辑变量，选择策略如下：

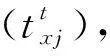
2 基于TPSO和属性相对变权决策的优选方法

2.1 改进的带有时变速度和极值排序的粒子群算法

本文设计了一种带有时变速度和极值排序的改进粒子群算法(Time-Varying Velocity Particle Swarm Optimization, TPSO)用于求解设备资源双层优化模型。

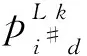
(20)

(21)

TPSO求解设备资源双层优化模型的步骤如下：

步骤1对企业设备单元进行整数编码，构建与其对应的个体。例如：当候选的组合为[EUNS6、EUNS2、EUNS14、EUNS8、EUNS3、EUNS5、EUNS9、EUNS12、EUNS13]时，其对应的整数编码为[6、2、14、8、3、5、9、12、13]。

步骤2初始化粒子群，设置算法的种群规模Gr，迭代次数N，时变权重值γ*和学习因子c1、c2j#等参数；随机赋予粒子群中每个粒子的初始速度和初始位置。

步骤3计算每个粒子的适应度值，对适应度值进行排序，搜索每个粒子经历的最好位置和群体经历的最好位置，并选取前n#个粒子的信息作为后续粒子群的更新依据。

步骤4按照式(20)和式(21)更新粒子速度和位置。

步骤5判断停止条件，若满足t≥N，则输出最优解集;否则返回步骤3。

通过调整γ*和n#值，TPSO表现出更强的局部和全局搜索能力，既保证了求解效率，又提高了优化效果。

2.2 基于属性相对变权决策的优选模型

企业设备资源优化是以客户(需求方)需求为驱动的资源服务化管理行为，通常需要根据客户需求偏好，从候选方案集合中选取综合评价最好的方案作为最终的实施依据。

然而候选方案的属性之间并非绝对独立，往往客户对属性的偏好存在关联依赖关系。以往研究较多采用属性固权决策方法，忽视了需求方的属性偏好间的关联依赖关系，不能保证决策结论的科学合理性。因此，本文在借鉴文献[14]研究成果的基础上，结合设备资源双层优化模型的特点，提出基于属性相对变权决策的优选模型。

设决策问题共有m′个候选方案，记为{Ak′|k′=1,2,…,m′}，需要分析的属性因素有n′个，记为{Hd|d=1,2,…,n′}，任意一个决策方案A在H1，H2，…，Hn′的属性值为x1，…，xn′，方案Ak′在属性因素Hi″上的状态值为xi″,j″，则主观偏好比率

i″=1,2,…,n′;j″=1,2,…,m′。

(22)

其中：Efj″,j″-Efj″,zc为首先希望在第fj″属性上将Azc的属性值改进为Aj″(Aj″为候选方案)的属性值所带来的偏好变化量；Ei″,j″=ωi″,j″×ui″(xi″,j″)，Efj″,j″=ωfj″,j″×ufj″(xfj″,j″)，ωi″,j″为对Aj″和Azc的摆幅置权方法判断信息所确定的第i″个属性Hi″的权重[15]，ui″(xi″,j″)为对Aj″在属性Hi″上的状态值xi″,j″所给出的单属性偏好，ui″(xi″,j″)∈[0,1]；Ei″,j″-Ei″,zc为在第i″属性上将Azc的属性值改进为Aj″的属性值所带来的偏好变化量，Azc为基于候选方案集合{Ak′|k′=1,2,…,m′}来构造的最差方案，Azc=(x1,zc,x2,zc,…,xn′,zc)；fj″为属性{Hd|d=1,2,…,n′}中首先希望将Azc的属性值改进为Aj″的属性值，fj″∈1,2,…,n′。

(23)

s.t.

∀k′∈1,2,…,m′;

∀i″∈{i#|i#=1,2,…,n′;ui#(xi#,j″)≠0},

ωi″,j″≥ε>0。

其中：ui″(xi″,k′)为对候选方案Ak′在属性Hi″上的状态值xi″,k′所给出的单属性偏好，ui″(xi″,k′)∈[0,1]；ε为非阿基米德无穷小；Zk′，j″为候选方案Ak′的综合偏好评价值。

由式(23)可知，属性权重之比ωi″,j″/ωfj″,j″是xi″,k′、xfj″,k′和℘j″(i″,fj″)的函数，因此ωi″,j″/ωfj″,j″会随着候选方案Ak′各个属性值的变化而变化；同样ωi″,j″/ωfj″,j″也会随着需求者关于方案Ak′各个属性值的偏好(体现在℘j″(i″,fj″))变化而变化；并且由于属性值x1，…，xn′是方案Ak′在各个属性上的特征描述，当需求者对属性的偏好存在关联关系时，需求者对各个候选方案的偏好也呈现出关联依赖关系，这种关系称为需求方在属性上的偏好关联依赖关系，因此构造各候选方案彼此之间互相影响的超矩阵rj″,t：

(24)

式中rj″,t为方案A1，A2，…，Am′在权重体系ωi″,j″下的相对偏好值。

A1A2…Am′

(25)

(δ1,δ2,…,δm′)T=

(26)

其中：I=(1,1,…,1)T为m′维列向量[16];c为循环周期，c∈N+；δk′为候选方案Ak′的优选排序权重，取值越大，方案越优。

3 仿真分析

3.1 仿真模型

以某型号往复式压缩机主要零件的生产制造任务(T)为例，对本文所提方法进行仿真验证。由于企业设备资源的有限性，需求方给任务T提出的要求为：生产总时间不超过450 h，生产总成本不超过6万元，T′任务的完成时间不超过300 h，T″任务完成时间不超过200 h，成本不超过2.5万元，设备单元协调度不小于3.6，任务匹配度不小于3.8。则该仿真实验的约束信息为：

max(ZTZ+time)≤450;

ZTZ≤300,time≤200;

Cost≤2.5,CostMAX≤6;

Z1≥3.8,Z2≥3.6。

(27)

T任务的名称和数量等信息如表1所示。

表1 T任务信息

表1表明，该T任务可分成T′和T″两种任务类型，求解时分别对应双层优化模型中的上层优化模型和下层优化模型。T′包括T1和T2等2个任务，T″包括T3、T4、T5、T6和T7等5个任务。各个任务具有一定的约束关系，如图2所示。

图2表明，T1包含t11曲轴和t12机身2个子任务，T2包含t21连杆和t22十字头2个子任务；T1和T2具有约束关系，即T2受T1任务的完成情况影响，T2必须在T1所有子任务完成后才能执行，且t22必须在t21完成后才能执行；T3，T4，T5，T6，T7受T2任务的完成情况影响，即T3～T7必须在T2所有子任务完成后才能执行。

企业中可选的生产车间PROWj,j=1,2,3,4,5，企业设备单元对T任务的加工时间和设置时间，企业设备单元之间的传递时间，T3～T7的任务匹配度指标以及企业设备单元之间的单元协调度等详细信息如表2～表5所示。表中数据信息是基于企业产品生产数据库而形成的数据。表2中,N表示对应的企业设备单元非可用;第1行第2列的1/2表示EUNS12对于任务t11的单位负载加工时间为1h，设置时间为2h；Number表示企业设备单元在候选集合中的索引号。表3中传递时间为0，表示企业设备单元属于同一个生产车间。表4中，设[LcAbCapInLoa]等指标的权重为：[ℑ1ℑ2ℑ3ℑ4ℑ5]=[0.160 0.237 0.166 0.254 0.183]，用e=[1.2,1.4,1.3,1.2,1.4,1.8,1.1,1.5,1.4,1.2,1.3,1.6,1.3,1.4]表示企业设备单元的单位时间成本。表5中S34表示可执行T3任务的3个企业设备单元与可执行T4任务的4个企业设备单元之间的单元协调度(例如：EUNS11、EUNS12、EUNS13与EUNS21、EUNS22、EUNS23、EUNS24)，为3行4列矩阵，其目的为量化企业设备单元之间的单元协调度值，其余表示类似。

表2 EUNS对T任务的单位负载加工时间MT和设置时间ST

表3 企业设备单元之间的传递时间TT

表4 T3～T7的任务匹配度指标信息

表5 企业设备单元之间的单元协调度

3.2 仿真结果与分析

在MATLAB R2012a运行环境下，采用TPSO求解式(27)。算法参数N=200，n﹟=4，c1=c2j#=0.8，Gr=500，以最大迭代次数为结束条件。仿真实验采用的参数是在适当范围内随机产生，求解结果如图3和表6所示。

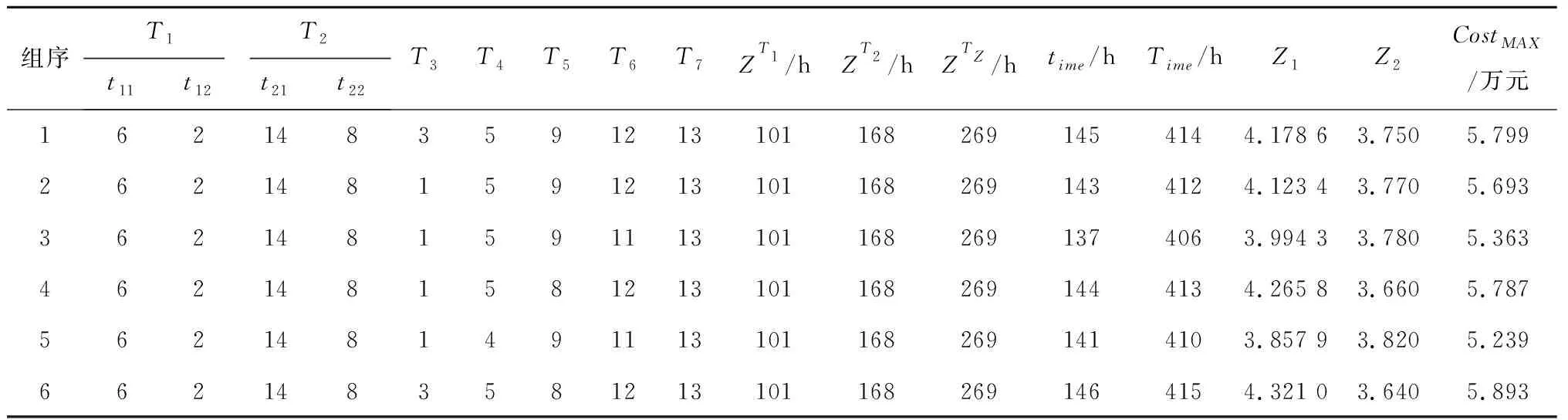
表6 候选方案编号及其对应指标数据

图3给出了T1、T2的最佳执行次序、加工时间、设置时间和传递时间。

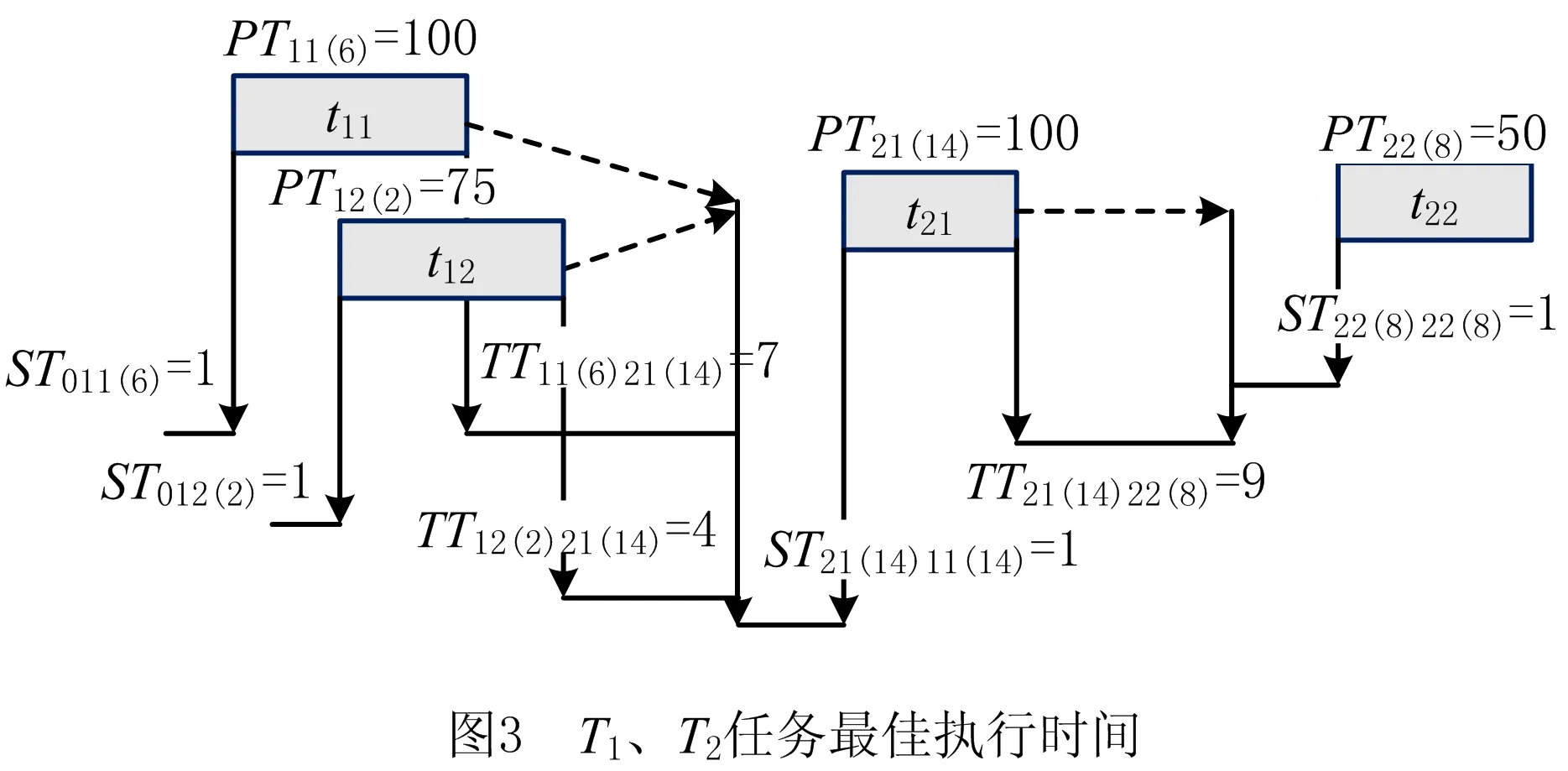
表6表明，共有6组候选方案，t11、t12、t21、t22、T3、T4、T5、T6、T7可选择由组序为1(不一定是最佳方案)的设备单元(即EUNS6、EUNS2、EUNS14、EUNS8、EUNS3、EUNS5、EUNS9、EUNS12、EUNS13)来执行。

此处获得的是候选方案集合{Ak′|k′=1,2,…,6}，需要依据任务匹配度(Z1)、执行总时间(Time)、单元协调度(Z2)和总成本(CostMAX)等方面(依次视为属性H1、H2、H3、H4)的综合评价信息优选出最佳方案。候选方案集合中的6组方案在4个属性上的属性值，即xi″,k′(i″=1,2,3,4;k′=1,2,3,4,5,6)(如表6)。

由于需求方可能会在H1、H2、H3、H4属性上存在偏好依赖关联关系，在给出具体数值偏好之前，需要向需求方做出调查，调查结果为：①当方案的任务匹配度或单元协调度比较好时，成本或时间可以适当大一些；②当方案的任务匹配度或单元协调度比较差时，即使成本或时间很小也不应该获得较高的评价结果。上述调查结果显示需求方关于方案的属性存在偏好依赖关联关系。

因此根据需求方的偏好信息，采用基于属性相对变权决策的优选模型，经偏好判断给出主观偏好比率(如表7)和各方案的单属性偏好值(如表8)；利用式(23)～式(26)可得方案A1，A2，A3，A4，A5，A6的选择排序权重及排列顺序如表9所示。

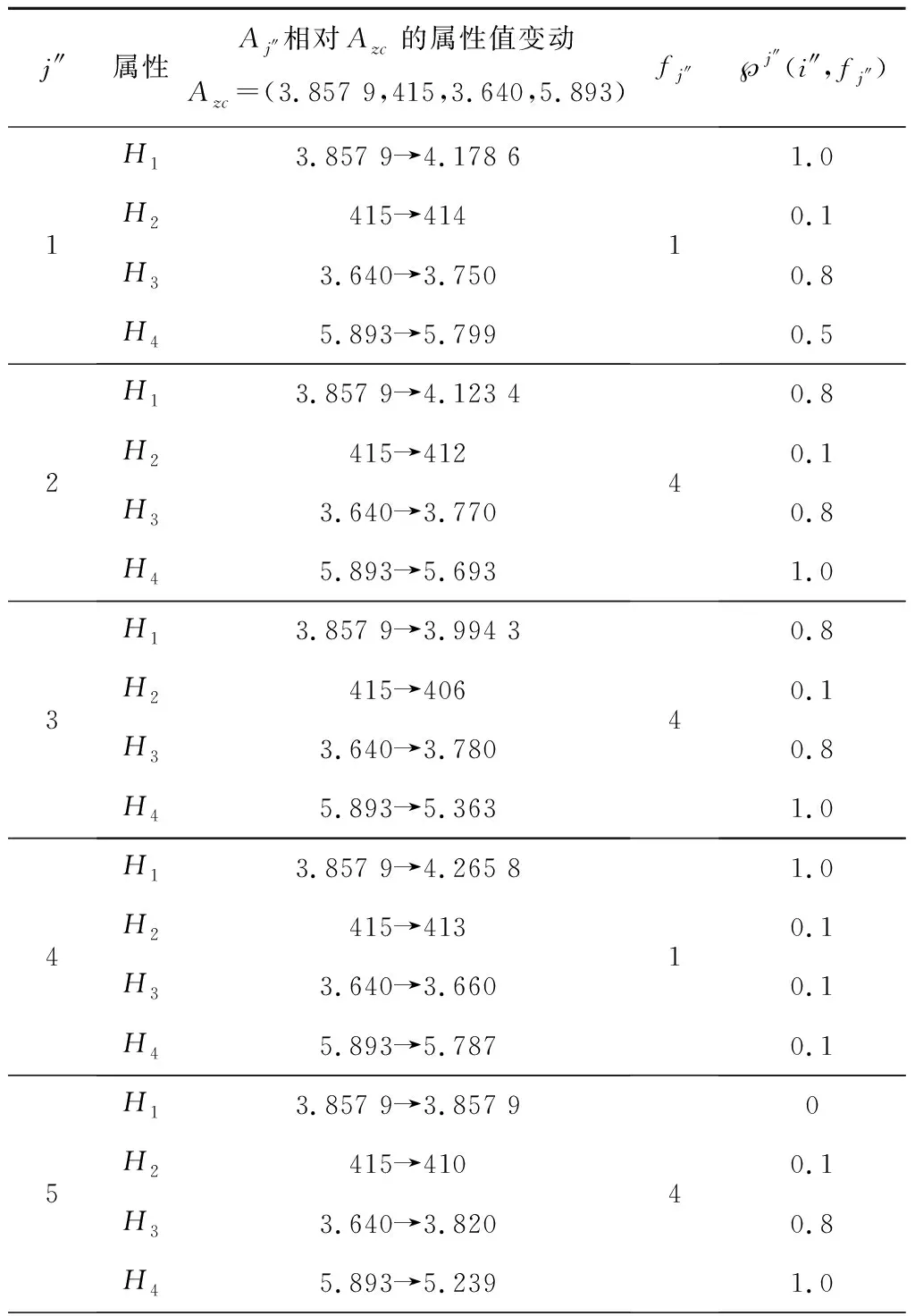
表7 主观偏好比率℘j″(i″,fj″)

续表7

表8 方案Ak′在属性Hd上的单属性偏好

续表8

表9 δk′的值及Ak′的优选排序

表7中第1列表示候选方案的组序，第2列表示属性类别，第3列表示各组候选方案相对最差方案Azc的属性值变动，第4列表示各组中主观偏好比率最大值所对应属性的编号，第5列表示主观偏好比率。

表9表明方案3为最佳的执行方案。通过分析表6和表9的数据信息，可以明显发现A3、A5的排序与需求方给出的调查结果②高度符合；A2、A5的排序与需求方给出的调查结果①高度符合。因此，该方法具有准确反映点依赖偏好关联关系的优势，并且可以很好地直接反映需求方的偏好结构。

表10表明，文献[12]可以得到较优的任务匹配度(Z1)，但是在任务总时间(Time)，单元协调效率(Z2)和总成本(Ct)方面求解较差；文献[5]可以得到较优的总成本(Ct)，但是在任务匹配度(Z1)方面求解较差；而本方法在任务总时间(Time)和单元协调效率(Z2)方面求解较优，在总成本(Ct)和任务匹配度(Z1)方面求解良好，并且在T1、T2的最佳执行时间(time)上，求解最优，表现出较好的求解性能。

表10 不同优选方法结果对比

上述分析表明，本文所提出的设备资源双层优化模型和多属性相对变权决策方法在解决设备资源优化配置问题上是合理有效的。

4 结束语

本文研究了基于任务分层策略和属性相对变权决策的设备资源组合服务优选方法，主要贡献如下：①提出了设备资源双层优化模型，该模型可以根据任务的不同功能需求对任务进行分层处理，强调任务功能需求的差异性及其关系的复杂性；②设计了基于时变速度和极值排序的粒子群算法，该算法能够有效提高模型求解精度和效率；③提出了基于属性相对变权决策的优选模型，该模型可以在优选过程中准确反映需求方在属性上的偏好依赖关联行为，规避优选参数赋值的随意性问题；④仿真实验表明，本文所提方法能够生成指导生产的综合评价最优的方案，该方法具有良好的性能。

综合考虑本文的研究内容和领域的发展，在后续研究中，将关注突发扰动等不确定因素对企业设备资源优化配置的影响，并展开深入研究。