风力发电系统的随机响应

梁相玲,叶正伟,秦旺,邓生文

(兰州交通大学 数理学院,甘肃 兰州 730070)

随着全球经济的增长,新能源的开发利用为世界能源危机与环境污染问题带来了解决方法,其中风能是之一。风能具有储存量大,短周期,低污染,范围广等特点,其主要应用于发电[1-3]。近年来,风力发电已涉及到各个领域,其效果得到了众人的认可,故国内外众多研究者都积极建模以便了解其原理与不足[4-5]。虽然通过多年来的研究分析使得风力发电系统已逐步完善,但是对风力发电系统在不同的工作环境中受到不确定自然条件的随机扰动的因素却考虑甚少,使得其输出功率与实际存在差异,故需要考虑和分析影响风力发电的因素,以便寻求风能被有效利用的措施。本文基于转子系统通过变换引进参激与外激得到随机风力发电系统,主要依据随机平均法与哈密顿理论以及最大李雅普诺夫指数法,分析随机响应即随机稳定性及其Hopf分岔,最后分析了分岔参数并展示其数值模拟图。

1 风电的随机动力系统

1.1 随机模型

本文基于机械系统风力涡轮转子系统,建立的简易风力发电系统模型如图1所示[6-7]。

图1 简易风力发电系统模型Fig.1 Simple wind power generation system model

转子方程为

(1)

式中:α是风力涡轮转子的角加速度;w是转子的角速度;δ是角度。所以可看到

Jα=Mm-Me-MD

(2)

式中J,Me,Mm,MD分别是发电机转子的惯性力矩(包括转子的原动力)，发电机主轴上的机械转矩，机械制动电磁转矩，阻尼力矩[6-7]。

由式(2)得

(3)

由于J可以由A表示,所以方程(3)可表示为

(4)

式中：A为惯性时间常数；f0为频率；δ单位为rad；Mm、Me和MD表示单位值。

力矩M由功率P表示为

(5)

故有

(6)

式中Pm,Pe,PD分别表示机械功率,电磁功率,阻尼功率,且都以单位值表示,其中基值以kV/A为单位。

其中

(7)

式中D为阻尼系数。

(8)

故所要研究的随机风力发电系统为[8-9]

β1δ(t)ξ(t)+β2ξ(t)

(9)

式中:ξ(t)是高斯白噪声,满足〈ξ(t)〉=0,噪声强度为2D;β1和β2是控制参数。

故可得系统的状态方程为

(10)

1.2 Hamiltonian 系统

令δ(t)=q(t),ω(t)=p(t),则式(10)可写为

(11)

则方程(11)的总能量为[10]

(12)

1.3 漂移系数与扩散系数

(13)

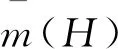
Ω={(q1,…,qn,p2,…,pn)|H

(q1,…,qn,0,p2,…,pn)≤H}

(14)

计算可得

(15)

(16)

2 稳定性分析

其稳定性分析主要依据最大Lyapunov指数法。首先需要把Lyapunov指数引用到随机微分方程中,需要做以下推导[13-14]：

(17)

(18)

为了得到其最大Lyapunov指数,可将方程(13)在H=0处表示成线性化形式:

(19)

其解为

(20)

则其最大Lyapunov指数为

(21)

故得

(22)

由式(22)可得系统在解H=0处,当λ<0时,系统是局部渐近稳定的;当λ>0时,系统是不稳定的;当λ=0时,系统发生分岔。

3 随机分岔

根据其扩散系数与漂移系数可得方程(11)的平均FPK方程为

(23)

则平稳概率即式(23)的解为

f(H)=CHηexp[-H]

(24)

式中C是归一化常数，且通过计算得

(25)

接着可得联合概率密度函数为

(26)

对于随机非线性动力系统,分岔类型可定义为D分岔和P分岔,两者完全由υ区分。选择γ作为参数描述随机分岔现象[14]。

1)D分岔点的计算:根据之前分析,当系统完成D分岔时υ=-1。则有

υ=cl-∂l=

(27)

2)P分岔点的计算:同理，P分岔点公式为

υ=cl-∂l=

(28)

4 数值模拟

选择γ作为分岔参数,令α=1,ρ=0.2,D=0.5,β1=0.5,β2=1。数值模拟平稳概率密度函数与联合概率密度函数在参数的不同取值下的图像如图2—图6所示。

图2 γ=0.25时的平稳概率密度函数Fig. 2 The stationary probability density function when γ=0.25

图3 γ取不同值时平稳概率密度函数 Fig. 3 The stationary probability density function with different value of γ

综合图2和图3可以看出，随着参数γ取值的减小其平稳概率密度函数是单调递减的且逐渐趋向平缓,即γ经过了临界点γ=0.208 3后函数的图象由单调递减变为单峰状函数,并且随着γ的持续减小,函数的谷峰逐渐趋向平缓,由此说明系统在临界点γ=0.208 3后发生了Hopf分岔。

图4 γ=0.208 3时的联合概率密度函数 Fig. 4 The joint probability density function when γ=0.208 3

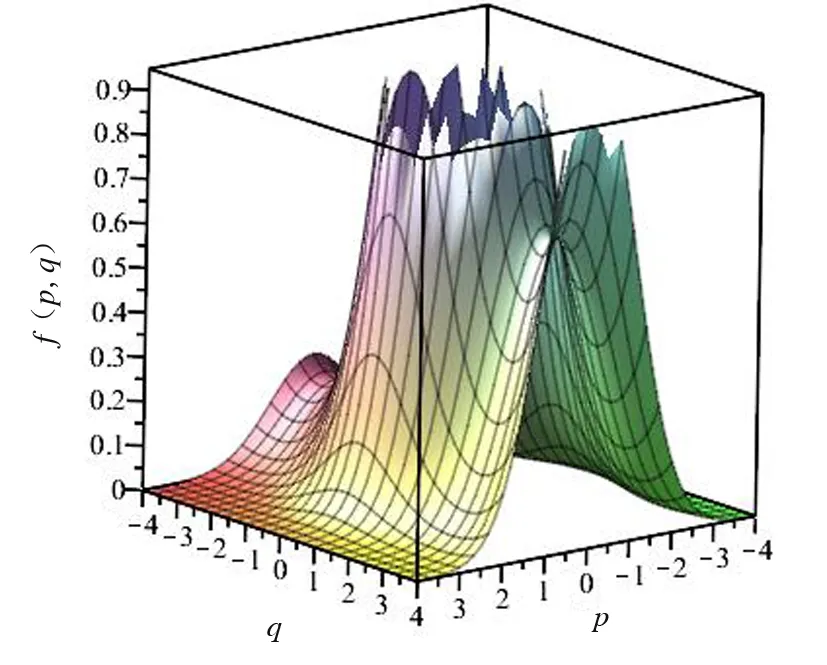
图5 γ=0.208时的联合概率密度函数Fig. 5 The joint probability density function when γ=0.208

图6 γ=0.2时的联合概率密度函数Fig.6 The joint probability density function when γ=0.2

综合图4、图5和图6可以看出，当γ=0.208 3时,函数图象是一个单峰状；当γ=0.208和0.2时,呈火山口状,这说明系统在临界点γ=0.208 3后发生了Hopf分岔。

5 结束语