一种基于UG/Motion实现曲线求导的方法
2021-11-10李玉胜董保香赵国庆王圣伟
李玉胜 ,董保香 ,赵国庆 ,王圣伟
(1.山东理工大学 机械工程学院, 山东 淄博 255049;2.淄博职业学院 电子电气工程学院, 山东 淄博 255314;3. 山东飞马索道缆车设备有限公司, 山东 淄博255000)
诸如凸轮机构等运动机构的设计,不仅仅需要实现机构预期的运动轨迹,而且还需要考虑其速度、加速度等运动规律特性。用解析法设计轨迹曲线时,因为有数学公式,求导容易,可方便地给出速度、加速度曲线;但用图解法设计轨迹曲线时,则无法给出求导后的曲线。因此,对于图解法,迫切需要一种利用已知轨迹曲线,求导得出速度、加速度曲线的方法[1-4]。本文给出一种连续曲线的求导方法。
1 导数的形成

2 利用UG/Motion求导的步骤
利用UG/Motion的求导步骤如下:
1)根据机构的运动要求,绘制位移轨迹曲线;根据需要绘制描述点t0(X0,Y0)、点t(X,Y),描述求导得出所需的Y方向运动曲线。
2)建立表达式变量Δx等。
3)创建运动仿真模型,定义连杆与运动副,并赋予传动运动副以驱动,特别要注意处理好描述求导得出的自定义函数。
4)定义点在线上幅、线在线上幅等约束条件。
5)创建标记点,用于追踪求导后的结果。
6)设置追踪,追踪上述标记点。
7)设置求解时间与步数等求解参数并求解。
8)运行动画,激活追踪,运行后获得追踪点,该点云就是描述求导后的轨迹点。
9)用样条曲线拟合点云,获得求导后的曲线。
3 sin(x)曲线的求导方法
以曲线sin(x),x∈[0,2π]为例,利用UG/Motion运动仿真模块,按照上述步骤,实现正弦曲线的求导。
1)在UG环境中,新建文件QiuDao.prt,为方便参数化驱动以及分析求导后的点云和曲线与正弦曲线之间的偏差,在QiuDao.prt文件中不绘制任何图形元素,把所有参数以及几何元素绘制在创建的motion.sim文件中。
2)进入运动仿真模块,新建运动仿真,选择动力学分析类型,仿真名为motion。
3)进入建模模块,利用表达式功能,建立如图1所示表达式:t=1,t是UG系统变量,是从0到1的动态变量;xt=2*pi()*t,pi()是UG系统内函数,xt的变化范围是[0,2π];yt_sin=sin(xt*180/pi()),UG中正弦函数自变量只能是度数,所以需要把弧度值转化为对应的角度值;yt_dos=cos(xt*180/pi()),正弦求导后对应的余弦曲线,用来检测求导结果的正确性与准确程度;zt=0,z轴值为0,正弦余弦曲线绘制在XOY平面内;Delta_X=2*pi()/360,用Delta_X表示增量Δx。

图1 表达式Fig.1 Expression
4)利用规律曲线,结合上述表达式,建立正弦曲线、余弦曲线,其中距离公差设置为0.000 1。
5)基于XOY平面创建草图,绘制如图2所示4条线段,线段端点与正弦曲线存在点在线上几何约束,用这4条线段与正弦的交点表示点t0(X0,Y0)与t(X,Y),两点之间水平距离设置为Delta_X。用这4条线段分别描述t0与t点沿着X、Y方向移动的连杆。在表达式对话框中,可随时修改Delta_X值,参数化驱动功能会立即更新两点之间的水平距离。

图2 连杆与运动副Fig.2 Links and joints
6)进入运动仿真模块,激活Motion仿真,创建如图2所示5个连杆。L_X用来表示t点沿X方向运动的所需连杆;L_Y用来表示t点沿Y方向运动的所需连杆;L_X0用来表示t0点沿X方向运动的所需连杆;L_Y0用来表示t0点沿Y方向运动的所需连杆。L_Dy是获取导数值所需连杆。所有连杆质量属性为自定义,质心选择各条线段靠近正弦曲线侧的端点,惯性CSYS采用绝对坐标系,质量为10;IXX、IYY、IZZ分别为10;IXY、IXZ、IYZ分别为0。
7)创建如图2所示平动副。J_X是连杆L_X的水平方向平动副,无基本连接杆。J_Y是连杆L_Y的竖直方向平动副,基本连接连杆为L_X。J_X0是连杆L_X0的水平方向平动副,无基本连接杆。J_Y0是连杆L_Y0的竖直方向平动副,基本连接连杆为L_X0。J_Dy是连杆L_Dy的竖直方向平动副,基本连杆连接为L_X0。
8)利用点在线上幅,把t与t0点约束到正弦曲线上。PointOnCurve_XY是把连杆L_Y用于表示点t(X,Y)的下端点约束到正弦曲线上。PointOnCurve_X0Y是把连杆L_Y0用于表示点t0(X0,Y0)的下端点约束到正弦曲线上。为保持精度,选择基于曲率的曲线参数化方法。
9)对J_X,J_X0分别设置驱动,皆为恒定平移模式,初速度值为2*pi(),单位为mm/s,即用1 s时间平动运动2*pi() mm的距离。
10)设置描述导数值的平动副J_Dy,驱动方式选择函数,函数类型为位移,采用函数管理器,插入函数math_func,值为点t(X,Y)与点t0(X0,Y0)在Y方向的差值,即只需要导入Y方向的位移,观察变量为位移,选择分量为Y,参考框架为绝对坐标系。在本仿真中,值为(DY(45,1,1)-DY(71,1,1))/Delta_X。
11)建立标记点Mark_Dy,连杆选择L_Dy,指定点为L_DY连杆靠近正弦曲线侧的端点,CSYS采用绝对坐标系。
12)设置追踪Tr_Dy,追踪对象为Mark_Dy,参考框架为绝对坐标系,目标层为10,并激活。
13)新建结算方案,时间为1 s,步数为360步,即用360步仿真完整个过程。在求解器参数中,设置动力学/运动学的误差为0.000 1,静力学误差为0.000 1。
14)求解。
15)设置图层10为工作图层。打开动画对话框,启用追踪封装选项,播放后,可看到随着点t(X,Y)与点t0(X0,Y0)沿着正弦曲线的移动,Mark_Dy标记点被打出,该点的Y值就是t0(X0,Y0)点的导数。
4 验证
1)将Mark_Dy的追踪点与余弦曲线对比,肉眼基本看不出区别。利用菜单“分析->偏差-->度量”偏差度量功能,把所有点与余弦曲线对比,如图3所示,可得出最大偏差值为0.006 2 mm,该值是在Delta_X为2pi()/360的前提下得到的,如果进一步缩小Delta_X值,则偏差会更小。图3显示了Mark_DY追踪点与余弦曲线的对比,为方便观察,追踪点只显示了大约一半。
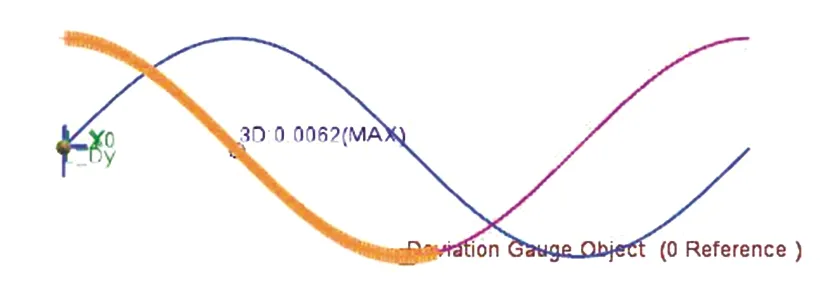
图3 点云与余弦曲线Fig.3 Points and cos(x) curve
2)利用样条曲线的拟合功能,把点云拟合成样条曲线,分析样条曲线与余弦曲线的误差,也为0.006 2 mm。样条曲线与余弦曲线的曲率梳对比如图4所示,左侧是余弦曲线的曲率梳,右侧是求导后曲线的曲率梳,可以看出求导所得曲线的曲率略有不光顺,但总体来说,没有比较大的突变。

图4 拟合样条与余弦曲率梳对比Fig.4 Curvature comb of cos(x) and spline
3)若着重曲率的光顺,可在拟合样条曲线时,略微放大公差,图5是曲线阶次为3,公差为0.01时的拟合样条曲线,该样条曲线与理论预先曲线偏差为0.011 2 mm,左侧是余弦曲线的曲率梳,右侧是拟合样条曲线的曲率梳,可以看出,两曲率梳基本没什么区别。

图5 拟合样条调整后的曲率梳Fig.5 Spline curvature after modification
5 结论
1)根据导数定义,利用UG的运动仿真功能,实现对sin(x)曲线的求导,验证了利用运动仿真功能对连续曲线求导方法的正确性。
2)给出了运动仿真得到的点云、拟合样条曲线与理论求导曲线的误差,若想提高精度,可减小Δx的变量值,直到满足工程应用需求。
3)对于非连续曲线,若非连续点恰好被Δx越过,也可以求出导数曲线。
