破解两类导数题中的双参问题

山东省青岛市第六十八中学 (266100) 王雅朦

在用导数解决关于函数、不等式、方程等问题中，常会出现一类双参问题，即给出x1,x2满足的范围求参数范围，或者是给出x1,x2的关系式解决其它问题，由于此类问题比较复杂，对数学思维能力要求较高.本文从典型题目的分析求解出发，通过点评揭示问题解决的一般方法及基本思路，供同学们参考．

一、两个函数中“存在”与“任意”求参数范围问题

1.两个都是“任意”条件下不等式成立

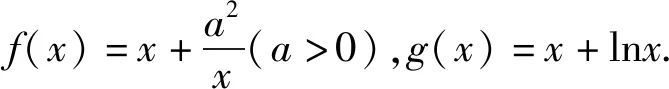
点评：由于题目中的双参x1,x2都是范围内的任意，所以不等关系就可以翻译成两个函数的最小值与最大值之间的大小关系问题，这个转化为解题指明了方向．

2.一个“任意”，另一个“存在”条件下的不等式成立

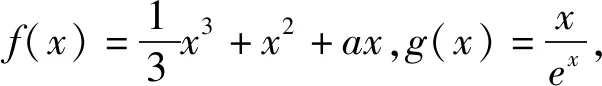
点评：由于题目中的双参x1,x2所对应的范围性质与上题不一样，首先必须确定是求两个函数的最大值还是最小值问题，实际上是两个函数最大值之间的比较．

3.使得两个函数值相等问题

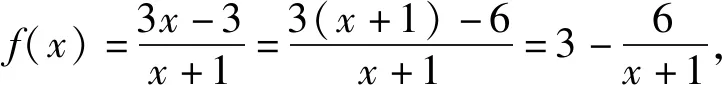
点评：由于题设是总存在两个函数值相等，即两个函数的值域含有交集，所以分别求出两个的值域就成为解决问题的主攻方向．

二、一个函数式的转化

1.证明不等式

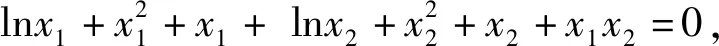
点评：在题目的证明过程中，根据已知条件对所给式子进行配凑，将其转化为与待证的结论相关的关系式是解题关键，它明确了下一步解题的方向．

2.恒成立求参问题

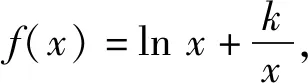
点评：通过对给出的双参不等式变形后再构造，推出了一个新函数的单调性，再利用此单调性转化出一个恒不等式，顺利解决了参数范围问题．一览操作过程，合理流畅．

3.求最大值问题

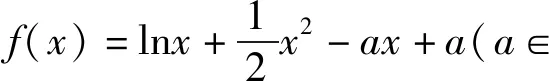
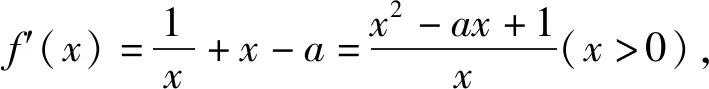
点评：此解法抓住已知条件，对待求最大值的式子进行化简、配凑，使其转化为求一个新函数的最大值问题，这里的有目的的转化是解题的关键．