一种低输入纹波电流的Buck变换器及其控制方法
2021-11-09袁义生刘文钦
袁义生,刘文钦
(华东交通大学电气与自动化工程学院,江西南昌330013)
在Buck 变换器及其衍生的正激、推挽、半桥、全桥变换器,亦或是逆变电路中,断续的输入电流是产生谐波电流和电磁干扰的主要原因。为了抑制输入侧断续电流带来的干扰,传统的方法是在输入侧加入无源滤波器。其采用电感、电容等无源器件来实现,具有结构简单、成本低、运行可靠性高的优点,但缺点是体积大并且引入无源器件的寄生参数降低了其滤波性能,以至于高频工作时会引起谐振现象。同时,磁芯的高频特性不佳会产生磁芯损耗[1-2]。
为了减小无源滤波器的体积,文献[3-5]提出了一些通过改进变压器设计的方法来实现滤波功能。文献[3]利用推挽变换器中变压器的漏感,加入交叉电容组成内置滤波器,进而实现输入电流连续。该方法的优点是不需要加入额外的电感器,因此减小了滤波器的体积,但该方法的适用范围仅限于隔离变换器,
而且输入侧电流纹波依然很大。文献[4]提出一种零纹波抑制技术,通过在有源箝位变换器的变压器上增加第三绕组,而后串联隔直电容的结构,使变换器输入侧纹波电流大部分通过第三绕组,有效实现了输入滤波。但其缺点是增加了变压器的损耗,导致变换器效率降低,而且其设计复杂、难度高,不具有普遍适用性。
有源滤波器因采用较小的无源器件和一些有源控制电路来代替大型无源元件,具有体积小、便于集成、动态特性好的优点,受到了广泛关注。文献[6]描述了有源纹波滤波器的结构和设计方法,并对用于消除纹波电流的有源滤波器四种基本电路结构进行了分类和比较。文献[7]提出一种用于DC-DC 变换器输入侧的有源纹波滤波器。通过利用电流传感器进行前馈和反馈控制,较好地实现了纹波电流抑制。但其缺点是电路结构复杂、效率低、高频性能差,而且对电流互感器的设计要求高,否则会降低系统的稳定性。
有源和无源滤波混合型滤波器[8]结合了两者的优点。用有源滤波器实现低频滤波,无源滤波器实现高频滤波,大大减小了无源滤波器的体积,改善了滤波特性。但其缺点是,混合滤波器一般采用变压器来注入反相纹波信号,这限制了滤波器的注入增益,降低了混合滤波器的高频抑制效果。
本文提出了一种低输入纹波电流的Buck 变换器。它采用了有源和无源滤波混合型滤波器方案,仅在传统电路中增加了一个功率管,通过将流经该功率管的电流控制成恒定直流,从而实现纹波电流的抑制。文中从工作原理、设计方法等多个方面进行了阐述,并进行了实验验证。
1 电路结构及工作原理
1.1 电路结构
所提出的低输入纹波电流的Buck 变换器如图1所示。电路分前后两级,阴影内为前级输入纹波电流抑制电路,由功率管QT,电容C1和电容C2构成。虚线框内为后级传统的Buck 变换器结构,由开关管Q1,二极管D1,电感L和输出电容Co构成。
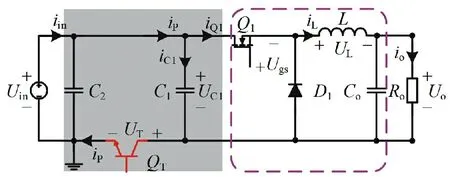
图1 低输入纹波电流的Buck变换器
1.2 工作原理
开关管Q1采用PWM 工作模式。功率管QT始终导通,工作在准饱和状态。Q1的驱动信号及其它关键波形如图2所示,从上到下依次为:开关管Q1的驱动信号Ugs,触发信号Utr,电感电流iL,流过功率管QT的电流iP,Q1的电流iQ1,电容C1 的电流iC1,电容C1的电压UC1,功率管QT的电压UT。其中,触发信号Utr是一个定频信号,其上升沿触发Q1导通。
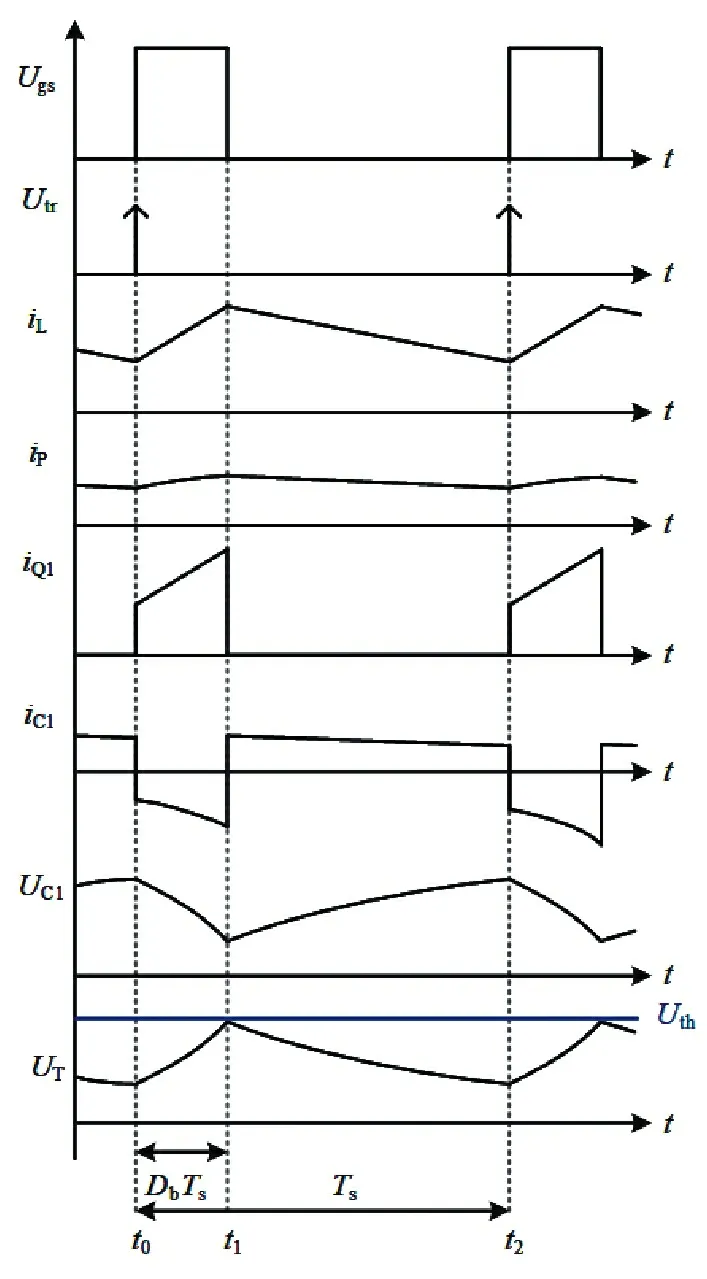
图2 驱动及开关波形
在开关周期内,电路分两个工作阶段。在分析中假设开关管Q1和二极管D1的导通压降为零。
(1)t0~t1阶段:在t0 时刻,触发Q1导通,iL和iQ1线性上升,电感L储能,电感两端电压UL可表示为:

由于iQ1>iP,iC1<0,电容C1放电,UC1下降,导致UT上升。此阶段有:
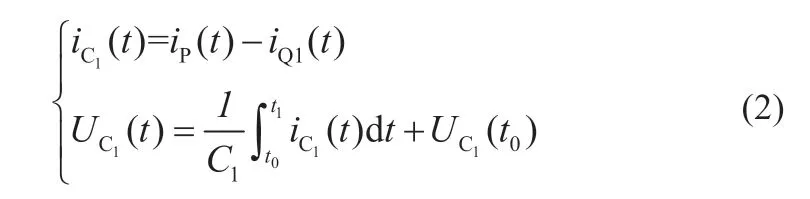
(2)t1~t2阶段:当UT上升达到峰值门槛电压Uth时,触发Q1关断。iP继续给电容C1充电,UC1上升导致UT下降,从而导致iP也下降。此阶段有:
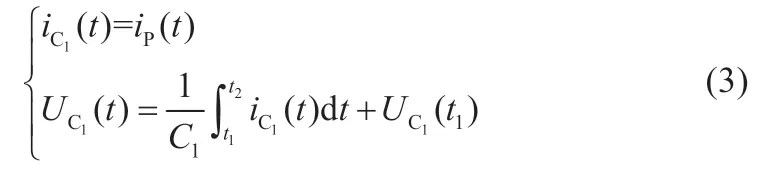
2 低输入纹波电流的原理
开关管Q1的电流iQ1是断续的,对输入侧干扰很大。将后级Buck 变换器等效为一个谐波电流源iQ1,作为前级电路的电流源。再将功率管QT等效为一个阻抗ZT。得到关于谐波电流的等效电路如图3所示。
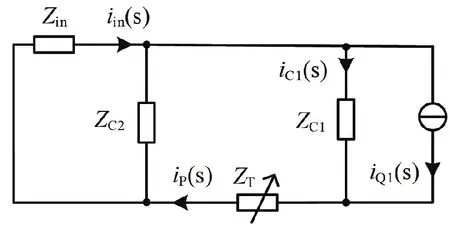
图3 谐波电流等效电路
根据基尔霍夫定律,输入电流iin与谐波电流iQ1的关系符合公式:
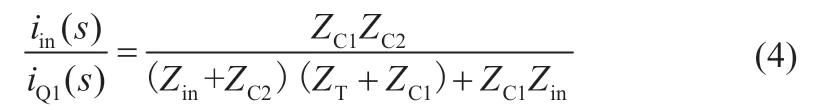
式中:Zin为输入电源阻抗;ZC1=1/(sC1),ZC2=1/(sC2)。
假设输入为理想电源,Zin=0。得到:
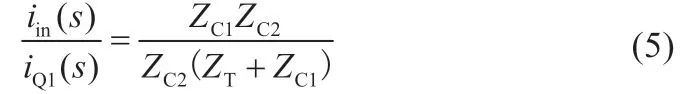
当采用C1=C2的对称结构时,上式继续化简为:

显然,当ZT>>ZC1时,iin就接近于0,输入侧电流就没有谐波电流,而只有直流电流。
以开关频率fs=145 kHz,占空比Db为0.26,形状如图4(a)所示的iQ1为例,其频谱特性如图4(b)所示。其分布规律为:
(1)频谱由间隔为fs的谱线组成,其以频率点(4n+2)fs(n=1,2,…)为轴,呈类似轴对称分布,形成分布宽度为4fs的包络,如图4(b)虚线所示;
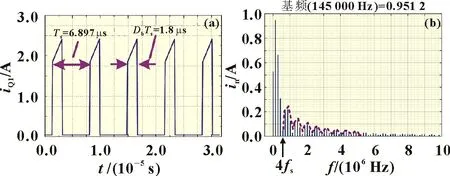
图4 谐波电流iQ1及其频谱特性
(2)最大谐波电流点在145 kHz 处,幅值in为0.951 2 A;
(3)随着频率的增大,各个包络所包含的谐波幅值减小。从4fs处开始,第一个包络至第八个包络所含各次谐波的总幅值分别为0.62、0.36、0.26、0.2、0.16、0.14、0.12 和0.10 A。
如果ZT只是阻值为RT的恒定电阻,则式(6)是一个简单的RC 滤波器,其截止频率fc为1/(2πRTC1)。为了抑制iin侧的谐波电流,截止频率fc必须小于开关频率fs,当fc=0.1fs时,开关频率的谐波可以衰减至1/10;当fc=0.01fs时,开关频率的谐波可以衰减至1/100。可以依据此特性来设计RTC1的时间常数。为了减小电容C1的容值体积,则希望RT更大。若要将谐波电流iQ1中开关频率145 kHz 的谐波衰减至1/50 倍(取对数为-34 dB),以电容容值6.4 mF 为例,RT需要约8.58 Ω,对应滤波器的频率特性如图5所示。

图5 滤波器的频率特性
谐波电流iQ1经过图5 特性的滤波器后,得到的输入电流iin及其频谱特性如图6所示。可见:
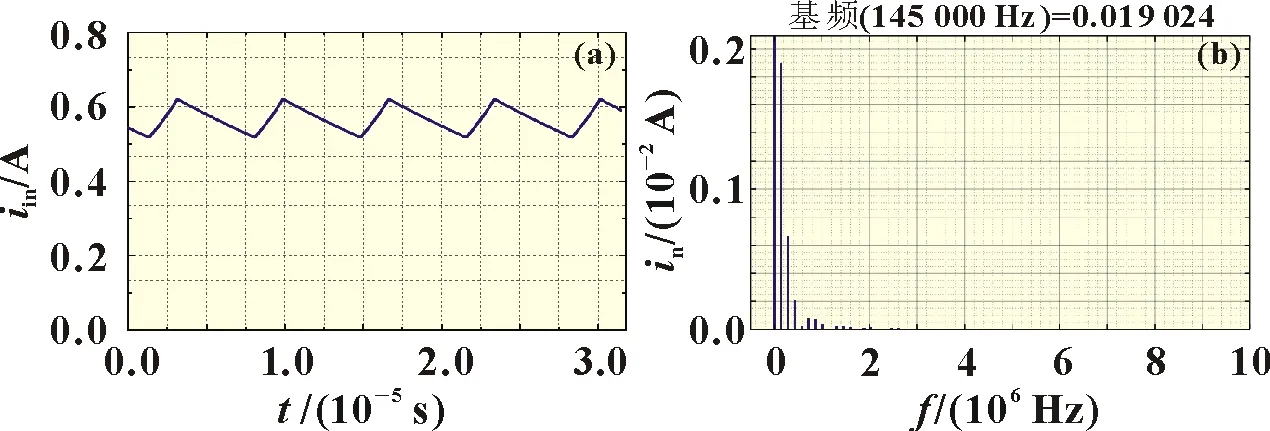
图6 输入电流iin及其频谱特性
(1)开关频率fs所在信号的幅值in为0.019 024 A,相较于iQ1衰减了50 倍。
(2)谐波主要分布在2 MHz 以下,高于2 MHz 的谐波被RC 滤波器衰减趋于零。
图7 绘出了iQ1和iin的波形。可见频率145 kHz、纹波为2.37 A的脉冲电流iQ1,经过一个RC滤波器后,得到的输入侧电流iin的纹波电流仅为102 mA,且电流连续,谐波量大大降低。
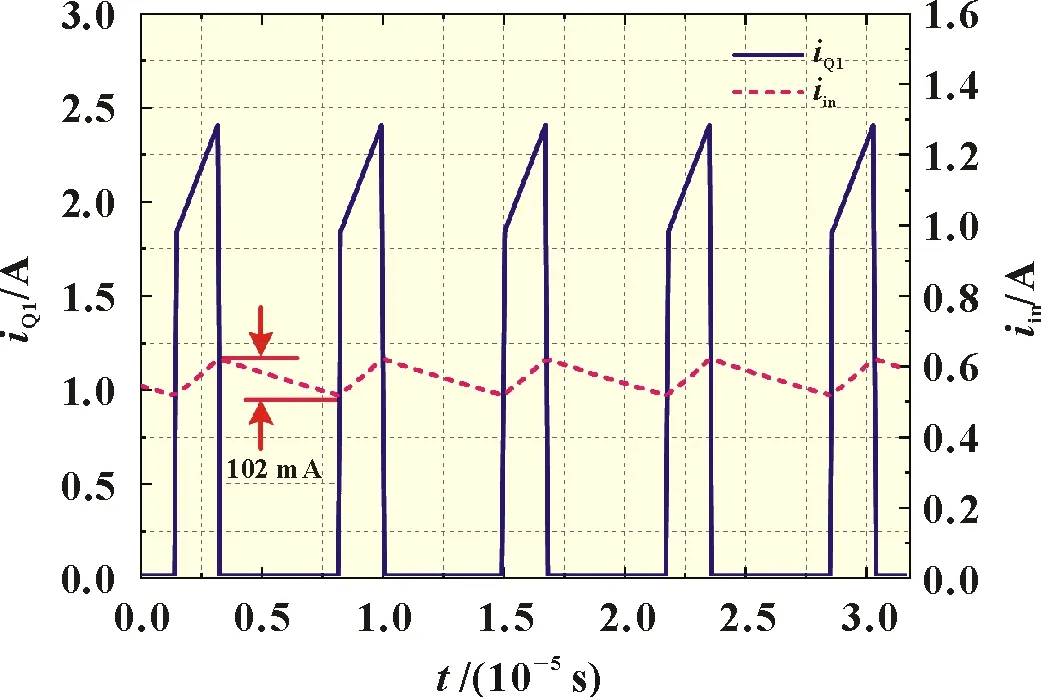
图7 iQ1与iin的波形
可见,如果功率管被控制成一个较大的恒定电阻时,也能够有效抑制谐波电流。但其缺点是损耗很大。以上述案例为例,iin的有效值为0.59 A,计算得到的RT上的损耗就达到了2.99 W,这大大降低了电路的效率。
理想的功率管QT的特性应该是直流阻抗小,而开关频率以上的谐波阻抗大,这样QT的损耗就小。从电流的角度看,则是流过功率管QT的电流iP应该控制成一个恒定直流源,则QT的谐波阻抗为无穷大,直流阻抗为0。
3 功率管QT及开关管Q1的控制
功率管QT及开关管Q1的控制框图见图8。控制框图包括两个控制环,它们是电压控制环和纹波电流抑制环。
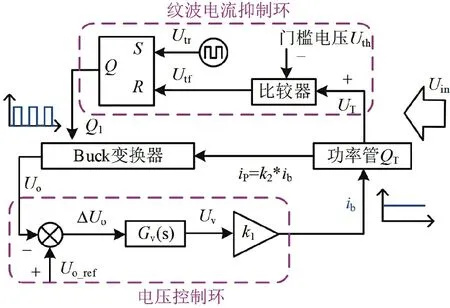
图8 控制框图
电压控制环控制输出电压Uo达到其设定值Uo_ref。Uo_ref减去反馈值Uo,得到的误差电压∆Uo经过电压环控制器Gv(s)后,得到误差控制电压Uv,再将其转换为功率管QT的基极电流ib,放大后得到功率管QT的通态电流iP。
从物理机制上讲,控制iP就是控制了满足维持输出电压Uo稳定所需的输入功率。而为了获得前一节所述的功率管QT的理想特性,在稳态下iP应该是一个恒定的直流电流。iP可以表示为:
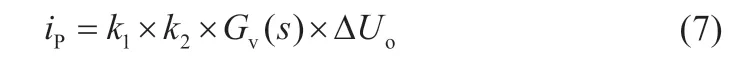
其中k1是V/I 转换系数,k2是功率管QT的电流放大倍数。在稳态下,Uo的直流分量完全等于Uo_ref。因此,主要是Uo的交流纹波分量∆Uo_ac会带来iP的波动,可以表示为[9]:

式中:Db是开关管Q1开关占空比。因此,为了抑制ΔUo_ac给iP带来的波动,控制器Gv(s)应该能够对ΔUo_ac进行足够的衰减。另一方面,Gv(s)对直流信号应有足够大的增益以获得输出电压直流量无静差。本文采用的控制器为:

控制器Gv(s)的穿越频率fc位于零点a与极点b对应的频率fa和fb之间,且fb小于开关管Q1的开关频率fs,以获得对ΔUo_ac足够的衰减比例。
纹波电流抑制环在抑制iP波动的同时,也控制开关管Q1的关断。由于在Q1开通过程中,UC1会下降,导致功率管电压UT上升,带来ip的波动。因此,设定一个UT的峰值门槛电压Uth。当UT达到Uth时,经比较器后产生1 电平送到RS 触发器的R端,其输出端Q置0,关断Q1,之后UC1上升,UT下降,iP随之略有下降。Q1的开通信号来自于定频触发信号Utr的上升沿。
4 功率管QT的特性需求
电流iP的特性取决于公式(7),以及功率管QT的特性。理想的纹波电流抑制效果,是希望iP只有恒定的直流电流。所以要抑制ib的波动,以及降低UT波动对iP波动的影响。因此,功率管QT的V/I 特性也很关键,要求QT工作在准饱和状态,即靠近饱和区的放大区附近,例如图9所示的阴影区域。换而言之,QT需要有较低的饱和压降。
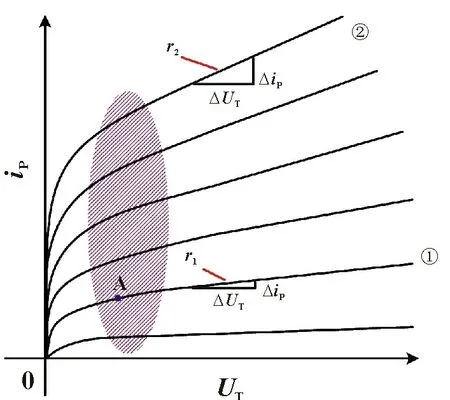
图9 三极管的输出特性
以三极管的V/I 特性曲线为例,见图9,横坐标UT表示其端电压,纵坐标iP表示流过功率管的通态电流。曲线的斜率定义了输出阻抗,输出阻抗r可以定义为:

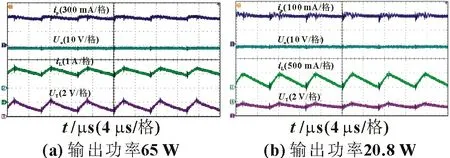
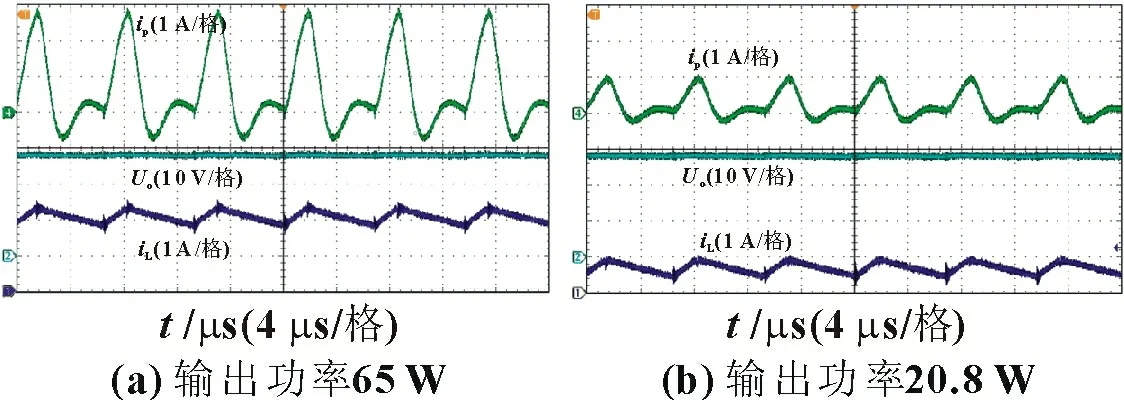
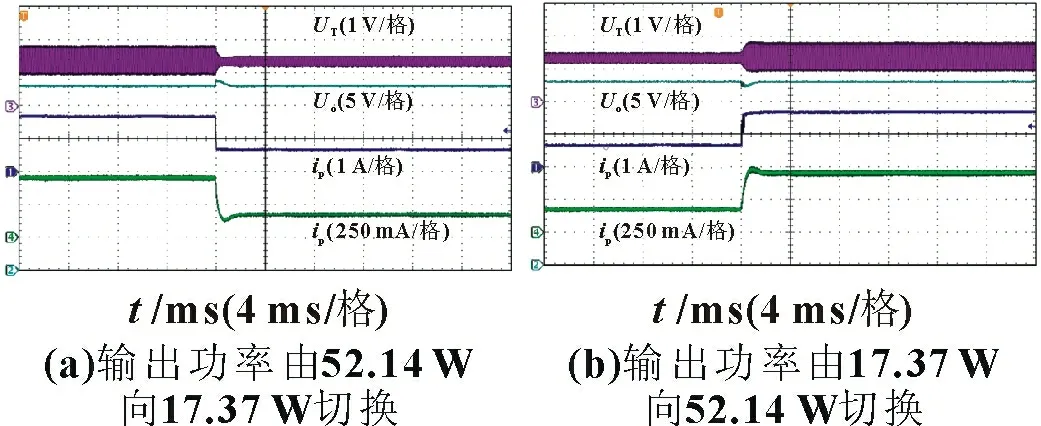
以曲线 ①、② 为例可以看出,同样的ΔUT下,曲线 ①ΔiP比②小得多,即输出阻抗r2 因此,设计时可以让功率管工作在曲线 ①的准饱和区内,例如图中的A 点,可以作为额定输入电流IP的工作点。忽略电路的损耗,IP可表示为: 另外,也应该尽量选择饱和压降低的功率管,以减小功率管的损耗,降低门槛电压Uth值。 为了验证所提出的低输入纹波电流的Buck变换器的工作原理和电路特性,制作了一台功率为65 W 的实验样机,电气参数及关键器件见表1。QT选FJAF4310,Q1选IRFB5615PbF。样机如图10所示。 表1 电气参数及关键器件 图10 实验样机 根据表1 设计参数,忽略功率管压降,计算得到ΔUo_ac=1.76 mV,由式(11)可以得到额定输入电流IP为0.59 A,查阅功率管QT的数据手册,得到其电流放大倍数k2为109.62。设计控制器Gv(s)、V/I 转换系数k1,使得电流iP含有的交流纹波ΔiP的大小为0.06 A。 控制器Gv(s)函数可以设计为: 式中:fc为穿越频率,1.49 kHz。经过控制器Gv(s),Uo的交流纹波分量ΔUo_ac衰减了8.92 倍。根据式(7),V/I 转换系数k1可以设计为2.77。 图11 显示了变换器在额定输出电压下,输出功率为65、42.25 和20.8 W 的主要波形。其分别为:流过功率管QT的通态电流iP、变换器输出电压Uo、电感电流iL、功率管QT的电压UT。 图11 所提电路样机测试波形 图11(a)为输出功率Po为65 W 时测得的稳态波形。测量得到电流iP是一个平均值为0.59 A,纹波电流峰-峰值仅为65 mA 的一个低纹波电流的直流电流。此时UT的平均值为1.46 V,功率管QT的损耗为0.86 W。谐波电流iQ1是电感电流iL的一部分,是一个峰值为2.4 A 的断续脉冲状电流。可见电路有效地将断续的谐波电流iQ1进行了滤波,得到了一个几乎完全直流的电流,大大降低了输入侧的干扰。 需要说明的是,由于纹波抑制电流环的响应延迟,当UT大于门槛电压Uth 时,开关管Q1不会立即关断,这导致UT会继续上升。实验测得的延迟时间为1.13 ms。 图11(b)为输出功率为20.8 W 时测得的稳态波形。此时电流iP的平均值为0.2 A,纹波电流峰-峰值为20 mA。此时UT的平均值为1.4 V,功率管QT的损耗为0.28 W。从电感电流iL 中得到谐波电流iQ1的峰值电流则高达0.95 A,可见轻载情况下谐波电流iQ1仍然得到了较好的衰减。 实验表明,纹波电流抑制电路的加入,有效地将Buck 变换器输入侧的断续电流进行了抑制,使得电源输入侧的电流变成了纹波很小的直流电流。为了简化分析,定义功率管QT的交流电阻为ΔUT/ΔiP,ΔUT表示其端电压的纹波大小,ΔiP表示流过它的电流iP的纹波大小。另外,从图11(a)可以得出,在额定电流IP=0.59 A 处,UT为1.46 V。可见,其直流等效电阻仅2.47 Ω。而根据谐波电流iQ1以及滤波后的电流iP的对比,其交流电阻为23.84 Ω。可见,在所提控制策略下,功率管的阻抗可变,其对直流信号的阻抗小,而对交流信号的阻抗很大,因而有较好的纹波抑制效果。从不同负载下功率管的损耗可以看出,所加入的纹波抑制电路在所设计的控制方案下,不仅满足了对纹波电流的抑制能力高的要求,也满足了系统功耗小的要求。 为了对比,将样机中的QT短路,只留下滤波电容C1和C2,测试了滤波效果,如图12所示。其中,iP表示流过原功率管QT位置处的电流、Uo表示变换器的输出电压、iL表示电感电流。 对比图11 和图12 可见,电容C1和C2仅仅对谐波电流iQ1中的高于开关频率的谐波成分明显衰减,开关频率的成分依然大量存在,导致电流iP的纹波较大。比较图11(a)与图12(a),输出功率同为65 W 时,传统电容滤波下iP的纹波大小为3.6 A,而加入QT后iP的纹波大小为60 mA。对比结果表明,本文提出的纹波抑制电路能够同时有效地抑制谐波电流iQ1中高于开关频率的成分和开关频率的成分。 图12 短路功率管QT,样机测试波形 图13 为额定输出电压下,变换器输出功率在17.37 W 至52.14 W 之间切换的测试波形。图中,io上升的时间为180 ms,下降的时间为40 ms。可以看出,由于功率的切换,电流iP的纹波大小变化极小,这表现了所提出的纹波抑制电路及其控制策略,使得变换器具有良好的动态响应。 图13 动态响应波形图 本文所提的一种低输入纹波电流的Buck 变换器及其控制方法,具有以下特点和优点: (1)结构简单,仅需要增加一个功率管。 (2)控制简单,无需额外增加控制电路,所增加的功率管和Buck 变换器的开关管共用控制电路。 (3)纹波电流抑制效果好。通过将功率管电流控制成近似的恒定直流源,有效地实现了谐波抑制。 (4)所提纹波抑制方案也可以推广用于其他Buck 类变换器。
5 实验验证

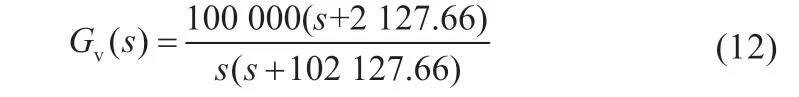
6 结论
