多中心共同配送与收集网络联盟优化问题研究

王 勇，罗思妤

(重庆交通大学 经济与管理学院，重庆 400074)

0 引 言

随着电子商务的快速发展和市场需求的不断增长，有限的物流服务设施资源与逐渐扩大的物流需求规模之间的矛盾日益凸显，城市物流网络对设施协同性和资源配置时效性提出了更高的要求。共享运输经济的兴起和第三方信息共享平台的推广，在创新配送与收集运营模式，提高网络资源利用和降低运营成本等方面进行了有效地探索和实践，物流网络合作联盟应运而生[1]。研究多中心共同配送与收集网络联盟优化问题，有助于促进共同配送与收集合作联盟构建和确保物流网络收益的合理分配，并有利于深化物流企业之间的有效合作，加强网络资源整合以及促进城市物流系统的资源共享与可持续发展。国内外学者的相关研究工作主要集中在多中心共同配送、多中心配送与收集以及物流合作联盟等方面。

多中心共同配送网络优化可以实现区域内配送路线的合理规划，有效减少配送路线交叉重叠的现象，降低物流网络运营成本。在多中心共同配送网络优化问题研究方面，LIU Guike等[2]设计了一种模拟退火算法，研究了多中心共同配送的绿色车辆路径问题，研究结果表明，共同配送相对于独立配送模式，可以有效降低运营总成本和碳排放量；LI Hongqi等[3]设计了一种基于节约算法的两阶段启发式算法，研究了考虑物流设施实时转运能力变化的两级多中心车辆路径问题；ZHANG Wenyu等[4]设计了一种基于矩阵运算的变邻域搜索算法，研究了多中心合作的多中心车辆路径问题，并通过不同目标优化间的比较验证了多目标优化的有效性; DENG Yirui等[5]设计了一种遗传-禁忌混合算法，研究了考虑集中运输的多中心合作的车辆路径问题，研究结果表明，合作环境下实施集中运输能提高资源利用率；盛虎宜等[6]提出一种改进的蚁群算法，研究了引入共同配送策略的集送货一体化车辆路径问题，研究结果表明，多中心共同配送策略能够有效缩短车辆行驶总距离和降低物流配送成本；王勇等[7]构建了最小化配送成本的整数规划模型，研究了多中心共同配送问题，并应用最小费用剩余节约方法(MCRS)对合作联盟的收益分配问题进行了研究。由此可知，多中心共同配送优化能够实现网络运输资源的优化配置，并有效缩短配送距离和降低物流运营总成本，而物流联盟收益的合理分配是促进联盟成员合作的有效方法。

在多中心共同配送网络优化研究的基础上，部分学者研究了多中心配送与收集网络优化问题。范厚明等[8]设计了一种自适应变邻域文化基因算法，研究了货物收集需求随机情况下的多中心共同配送与收集车辆路径优化问题；A.SORIANO等[9]提出一种改进的自适应大邻域搜索算法，对多周期的多中心配送与收集问题进行了研究，并通过对多中心离散需求的集中运输，实现网络服务效率的有效提升；H.HERNNDEZ-PÉREZ等[10]构建了最小化网络运营成本的优化模型，并设计一种分支定界算法研究了合作的配送与收集问题；徐东洋等[11]引入贪婪思想设计了基于大规模邻域搜索的迭代局部搜索算法，研究了多中心配送与收集车辆路径优化问题；S.UMAR SHERIF 等[12]研究了货物库存成本、运输成本和碳排放成本在内的运营成本最小化的二级多中心配送与收集绿色车辆路径优化问题；B.OLGUN等[13]设计了一种基于局部搜索和可变邻域下降方法的超启发式算法，研究了多中心配送与收集的绿色车辆路径问题。由此可知，多中心间离散需求的集中运输和转运调度可以有效减少长距离配送(收集)和交错运输等现象，而合理化的集中运输和转运调度是多中心共同配送与收集网络联盟构建的关键。

构建稳定的网络联盟，可以促进配送与收集中心的有效合作，亦为提升网络服务能力的重要途径之一。WANG Yong等[14]设计了一种改进的粒子群-蚁群混合算法，研究了两级多中心配送与收集网络联盟优化问题，研究结果表明，建立配送与收集合作联盟比独立的配送网络联盟更能有效提高物流网络的服务效率和降低车辆使用数；YU Yang等[15]提出了一种精确算法，证明了配送中心和收集中心可以通过线路合作有效缩短车辆行驶距离和降低配送与收集运营总成本，并提出了一种改进的Shapley模型进行合作联盟成员的利润分配；ZHANG Mengdi等[16]构建了一个最大化联盟利润的整数线性规划模型，研究了多中心合作的物流网络联盟优化问题，并探讨了合作程度与合作联盟规模对物流网络的影响；LIU Lin等[17]提出了一种自适应大邻域搜索算法，研究了两级多中心合作的车辆路径优化问题，研究结果表明，全局合作相对于局部合作可以有效降低物流网络运营总成本；H.FARVARESH 等[18]设计了一种分层启发式算法，研究了带时间窗的共同配送与收集车辆路径问题，并提出了联盟序列选择方法和探讨了合作联盟稳定性。文献[14]～[18]主要为集中在合作联盟网络构建和收益分配模型选择等方面的研究，而在收益分配机制和多中心共同配送与收集网络联盟相结合方面的研究还有待进一步深入。

笔者研究了多中心共同配送与收集网络联盟优化问题。首先，建立了网络运营总成本最小和车辆使用数量最少的双目标优化模型，并提出了基于k-means聚类算法的Im-NSGA-Ⅱ混合算法，在混合算法中设计了贪婪算法生成高质量初始可行解，并利用精英保留策略提高了混合算法的寻优和收敛能力；其次，运用MCRS方法对合作联盟利润进行分配，并根据严格单调路径原则和雪球理论对合作联盟稳定性进行讨论；最后，通过实例分析讨论了不同合作模式对多中心配送与收集网络的成本与车辆使用数的影响，进而为解决物流共同配送与收集问题提供新的方法和途径。

1 问题描述

合理的城市配送和收集网络运营体系是整个物流网络降本增效的基础。长期以来，由于各物流设施的建设时序不同、运力能力有限、客户服务契约关系限制等因素，导致配送与收集过程中交错运输、长距离运输等不合理运输现象频发。利用互联网等新型智能技术在线组建配送与收集合作联盟，构建多中心共同配送与收集网络运营体系，能够有效降低多中心配送与收集网络的运营成本和提高网络资源利用率；而合理的利润分配机制能够提高配送与收集网络的稳定性和可靠性，促进物流网络的可持续发展。

多中心共同配送与收集车辆路径优化问题聚焦于考虑配送与取货需求服务关系变化和货物调度运输，实现配送中心与取货中心间的物流资源共享，从而降低配送与取货网络运营成本，减少配送与收集车辆数量。多中心共同配送与收集网络优化前后对比如图1。在多中心共同配送与收集网络优化前〔图1(a)〕，配送中心、收集中心各自独立运营，导致了各个配送中心、收集中心的服务网络交错重叠以及交错运输、长距离运输、违反客户时间窗等现象的存在。在多中心共同配送与收集网络优化后〔图1(b)〕，由独立运营导致的各项问题得到相应地解决。一方面，将配送客户或取货客户分配给距离较近的物流设施，合理地划分配送与收集服务区域，减少配送与收集网络中的交错运输与长距离运输等现象；另一方面，安排卡车集中调运各个配送中心与收集中心间的货物，有效地协调各个配送与收集区域间的客户需求与物流资源，进而实现网络资源的集约化，减少配送与收集车辆数量。同时，优化配送与收集服务区域内与区域间的车辆路线，能够快速响应客户的时间窗需求，降低网络运营总成本，并提高客户满意度。如图1(b)，将原本由DC2进行服务的客户C5改变为由DC1进行服务，能够使客户C5的时间窗要求得以满足；车辆从DC1出发完成客户C4和C5的配送任务后，执行客户C23和客户C24的收集任务，随后返回取货中心PC1，能够减少配送与收集车辆数量。

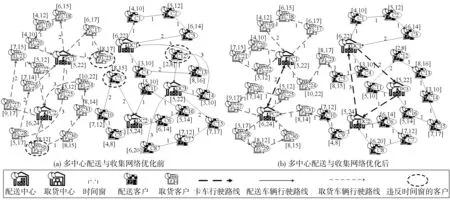
图1 多中心共同配送与收集网络优化前后对比Fig. 1 The comparison before and after the multi-center joint distribution and pickup network optimization

图1中实线与虚线上的数值分别表示卡车与车辆的行驶时间，配送中心与取货中心时间窗的开始时间为卡车和车辆的出发时间。假设卡车单位时间的运输成本为45元，配送与收集车辆单位时间的运输成本为40元，违反客户时间窗的单位时间的惩罚成本为35元，每辆卡车的维护成本为18元，每辆配送与收集车辆的维护成本为15元，每个配送中心与收集中心参与合作时能够获得100元合作激励。表1展示了多中心共同配送与收集网络优化网络前后的运营指标对比。结果表明，多中心共同配送与收集网络优化消除了违反客户时间窗的现象，降低了配送与收集成本、配送与收集车辆维护成本，进而使运营总成本从2 705元降低至2 111元，使配送与收集车辆使用数量从11辆降低为9辆。

表1 多中心共同配送与收集网络优化前后各项成本与车辆使用数对比Table 1 Comparison of the costs and the number of vehicles before and after the multi-center jointdistribution and pickup network optimization

2 模型建立

2.1 符号定义

为构建多中心共同配送与收集网络优化数学模型，笔者定义了多中心共同配送与收集网络中的物流设施、客户、车辆等集合及物流设施容量、客户需求、车辆行驶时间等变量。多中心共同配送与收集网络优化问题的变量定义如表2。

表2 模型相关变量定义Table 2 The definition of the related variables for the model

2.2 模型构建

以多中心共同配送与收集网络运营总成本H最小化和配送与收集车辆使用数量U最小化为目标，建立多中心共同配送与收集双目标优化模型：

minH=H1+H2+H3+H4

(1)

(2)

式中：H1为仅执行配送任务和仅执行收集车辆的运输成本和维护成本；H2为同时执行配送和收集任务车辆的运输成本和维护成本；H3为用于配送中心与收集中心间货物调运卡车的运输成本和维护成本；H4为配送中心与收集中心的固定成本和配送与收集车辆违反客户时间窗的惩罚成本，并考虑合作激励，如式(3)～(6)：

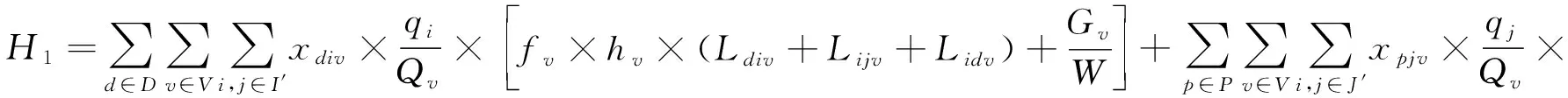
(3)

(4)

(5)

(6)

约束条件：

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

αi≤tiv≤βi(∀i∈I,∀v∈V)

(20)

t′mv+tmiv-M(1-xmiv)≤tiv(∀m∈M,∀i∈I,

i≠m)

(21)

t′mv+tmiv+M(1-xmiv)≥tiv(∀m∈M,∀i∈I,

i≠m)

(22)

αj≤tjv≤βj(∀j∈J,∀v∈V)

(23)

t′nv+tnjv-M(1-xnjv)≤tjv(∀m∈M,∀j∈J,j≠m)

(24)

t′nv+tnjv+M(1-xnjv)≥tjv(∀m∈M,∀j∈J,j≠m)

(25)

t′iv+tijv-M(1-xijv)≤atjv(∀i,j∈C,i≠j,∀v∈V)

(26)

t′iv+tijv+M(1-xijv)≥tjv(∀i,j∈C,i≠j,

∀v∈V)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

Zd={0,1} (∀d∈D)

(35)

Zp={0,1} (∀p∈P)

(36)

ydd′s={0,1} (∀d,d′∈D,d≠d′,∀s∈S)

(37)

ypp′s={0,1} (∀p,p′∈P,p≠p′,∀s∈S)

(38)

xdiv={0,1} (∀d∈D,∀i∈I,∀v∈V)

(39)

xpjv={0,1} (∀p∈P,∀j∈J,∀v∈V)

(40)

xmiv={0,1} (∀m∈M,∀i∈I,i≠m,∀v∈V)

(41)

xnjv={0,1} (∀n∈N,∀j∈J,j≠m,∀v∈V)

(42)

xijv={0,1} (∀i,j∈C,i≠j,∀v∈V)

(43)

Edid′={0,1} (∀d,d′∈D,d≠d′,∀i∈I)

(44)

Epjp′={0,1} (∀p,p′∈P,p≠p′,∀j∈J)

(45)

式(7)表示每个配送客户仅由一辆从配送中心出发的车辆进行服务；式(8)和式(9)表示每个收集客户仅由一辆从收集中心出发的独立执行收集服务的车辆进行服务，或者仅由一辆同时执行配送和收集服务的车辆进行服务；式(10)～(12)表示配送与收集车辆在服务一个客户后，离开该客户去服务下一个客户；式(13)～(14)分别表示独立执行配送服务车辆和独立执行收集服务车辆的装载量不超过车辆的最大装载量；式(15)表示同时执行配送和收集服务车辆的装载量不超过车辆的最大装载量；式(16)～(17)表示卡车的装载量不超过最大装载量；式(18)～(19)分别表示配送和收集的货物量不超过配送中心和收集中心的最大容量；式(20)表示每辆配送车辆在配送客户的时间窗内对其进行服务；式(21)～(22)表示配送车辆到达配送客户的时间；式(23)表示每辆收集车辆在收集客户的时间窗内对其进行服务；式(24)～(25)表示收集车辆到达收集客户的时间；式(26)～(27)表示同时执行配送和收集的车辆到达收集客户的时间；式(28)～(30)表示配送与收集车辆的行驶时间不超过路线允许的最大行驶时间；式(31)～(32)表示集中调运的货物运输量等于改变客户服务关系的客户总需求量；式(33)～(34)表示消除线路上的子回路；式(35)～(45)表示决策变量。

3 基于k-means聚类算法的Im-NSGA-Ⅱ混合算法

为了求解多中心共同配送与收集双目标优化模型，笔者提出了基于k-means聚类算法的Im-NSGA-Ⅱ混合算法。首先，设计k-means聚类算法对多中心配送与收集网络的服务区域进行合理地划分，将客户分配给临近的物流设施；其次，根据k-means聚类算法的结果，设计贪婪算法在各个服务区域内与服务区域间生成初始的车辆行驶路线；最后，利用NSGA-Ⅱ对车辆行驶路线进行优化，进而生成多中心配送与收集优化线路。基于k-means聚类算法的Im-NSGA-Ⅱ混合算法的流程如图2。

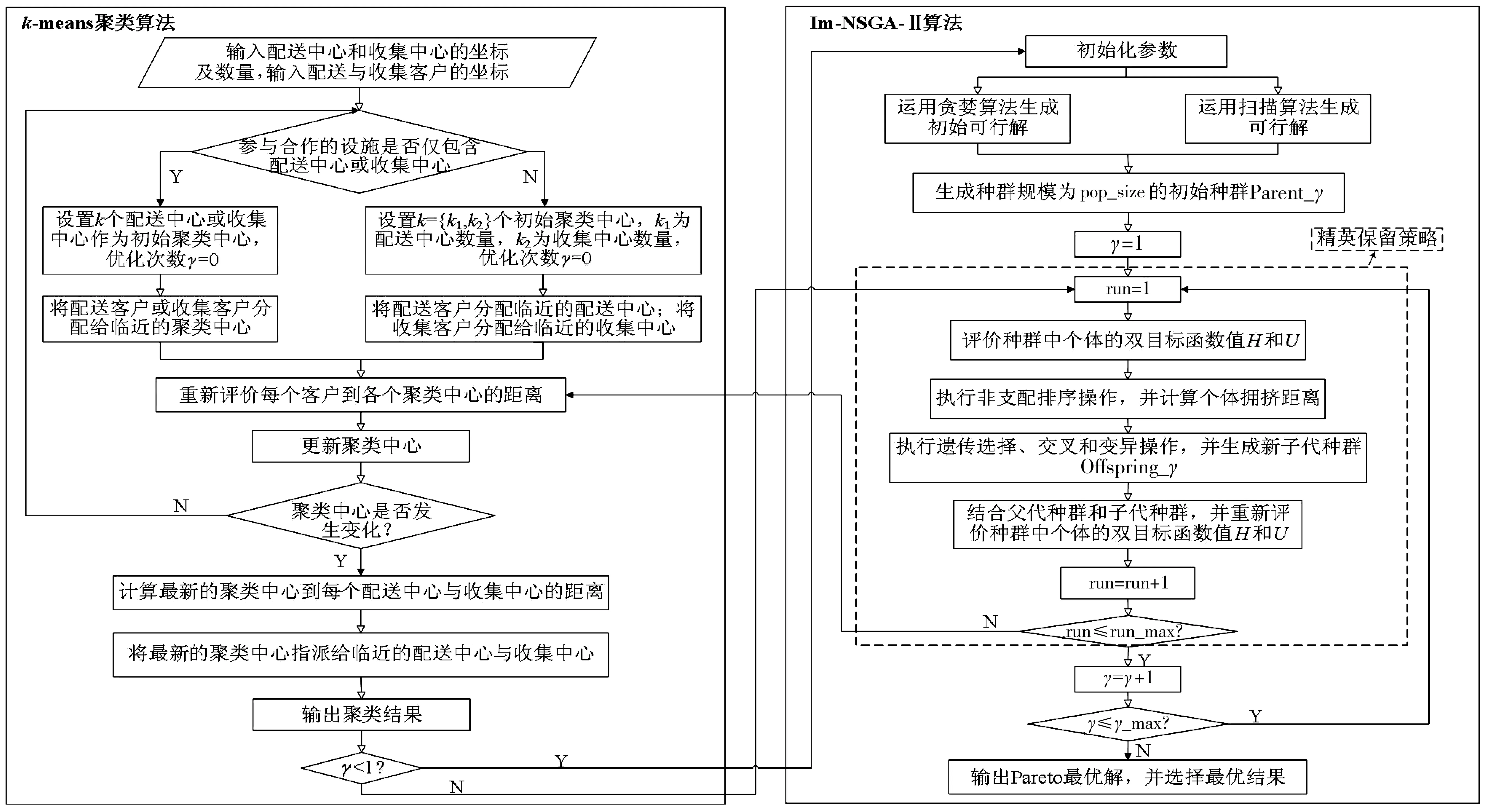
图2 基于k-means聚类算法的Im-NSGA-Ⅱ混合算法流程Fig. 2 Flow chart of the hybrid algorithm based on Im-NSGA-Ⅱ and k-means clustering algorithm

3.1 k-means聚类算法

对客户进行聚类分析，合理地划分多中心共同配送与收集网络中各中心的服务区域，一方面能够减少多中心共同配送与收集网络中的交错运输、长距离运输等现象，降低多中心共同配送与收集网络运营总成本；另一方面将多中心车辆路径优化问题转化为单中心车辆路径优化问题，降低了混合算法的计算复杂度，并通过将客户分配给临近的设施，减少初始可行解的总行驶距离，加快混合算法的搜索速度。k-means聚类算法过程如下：

Step 1输入配送中心和收集中心的数量和位置坐标，输入配送客户和收集客户的位置坐标。

Step 2判断参与合作的物流设施是否仅包含配送中心或者收集中心，如果满足判断条件，则转到Step 3；如果不满足判断条件，则转至Step 4。

Step 3设置k个配送中心或者收集中心作为初始聚类中心。

Step 4设置k={k1,k2}个配送中心和收集中心作为初始聚类中心，其中包含k1个配送中心，k2个收集中心。

Step 5计算每个客户到初始聚类中心的距离，将每个客户分配给临近的聚类中心。

Step 6更新k个聚类中心，重新评价每个客户到新聚类中心的距离。

Step 7重复Step 5～Step 6, 将所有客户逐一分配给聚类中心，且聚类中心稳定不变。

Step 8计算最新的聚类中心到每个配送中心与收集中心的距离，将各个聚类中心的客户簇群分配给临近的配送中心或收集中心。

Step 9输出聚类结果。

3.2 基于k-means聚类算法的Im-NSGA-Ⅱ混合算法的实现过程

根据“先聚类，后优化”的思想[19]，运用基于k-means聚类算法的Im-NSGA-Ⅱ混合算法求解多中心共同配送与收集双目标优化模型，相关变量定义如表3。

表3 算法相关变量定义Table 3 The definition of the related variables for the algorithm

混合算法的具体实现过程如下：

Step 1设置最大优化次数γ_max、最大迭代次数run_max、种群规模pop_size、染色体选择概率ρsel、染色体交叉概率ρcro以及染色体变异概率ρmut等算法相关参数。

Step 2设计贪婪算法生成初始可行解。运用扫描算法[20]生成初始解直至初始父代种群Parent_γ的种群规模达到pop_size大小，此时设置γ=1，run=1。Step 2.1～Step 2.3为贪婪算法生成初始可行解的过程：

Step 2.1计算任意两个配送客户或者收集客户节点之间形成的路径的距离，并按距离值分别将路径从小到大排序。

Step 2.2依次判断路径是否为子路径，如果是子路径即添加到当前路径中，否则直接判断下一路径。判断子路径的规则：①添加该路径后不会使任何节点的连接边数量大于2；②添加该路径不会使路径闭合；③添加该路径生成的单条路径中的客户总需求不超过车辆最大装载量；④添加该路径时满足客户的时间窗要求。

Step 2.3执行Step 2.2直到没有子路径存在，此时将每条路径的两个端点分别与配送中心或收集中心连接形成闭合回路。

Step 3评价初代父代种群Parent_γ中每个个体的双目标函数值H(网络运营总成本)和U(配送与收集车辆使用数)，并构造Pareto非支配解集[21]，执行非支配排序操作以及计算个体的拥挤距离。

Step 4执行精英保留策略，根据适应度函数值，选择当前初代父代种群Parent_γ中适应度值较高的一定数量的个体记录为精英个体。此类精英个体得以保留，不参与随后的遗传选择、交叉和变异操作。

Step 5对非精英个体执行遗传选择、交叉和变异操作以生成子代个体。过程主要包括：运用锦标赛选择方法选择父代个体[22]；采用部分映射交叉算子对父代个体进行交叉操作；采用反转突变算子对个体基因进行变异操作[23]。

Step 6在Step 5生成的子代个体中，用Step 4保留的精英个体替换遗传交叉和变异操作后适应度值较低的个体，以此生成新子代种群Offspring_γ。

Step 7结合初代父代种群Parent_γ和新子代种群Offspring_γ生成新一代种群，新种群大小为2倍pop_size，并根据新种群中每个个体非支配排序的Rank值和拥挤距离，选择个体组成新一代父代种群Parent_(γ+1)，Parent_(γ+1)种群大小为pop_size。

Step 8令run=run+1，判断当前迭代次数run是否达到最大值run_max。若run≤run_max，返回k-means聚类算法Step 6；若run≥run_max，则转到该混合算法Step 9。

Step 9令γ=γ+1，判断当前优化代数γ是否达到最大值γ_max。若γ≤γ_max，返回该混合算法Step 3；若γ≥γ_max,结束混合算法的循环迭代操作。

Step 10输出Pareto最优解集，在Pareto最优解集中选择最优解[23]，结束算法。

3.3 算法检验

为了验证笔者提出的Im-NSGA-Ⅱ混合算法的有效性，将Im-NSGA-Ⅱ混合算法与NSGA-Ⅱ[24]和多目标遗传算法(MOGA)[25]进行比较。实验数据采用Cordeau标准算例[26]，并根据多中心共同配送与收集网络特征进行修改，如表4。根据已有相关文献[27,28]，设置算法参数如表5。考虑到启发式算法结果存在随机性, 每组实验运算10次，并选取10次运算结果中的最优解和对应的运算时间进行对比，如表6。

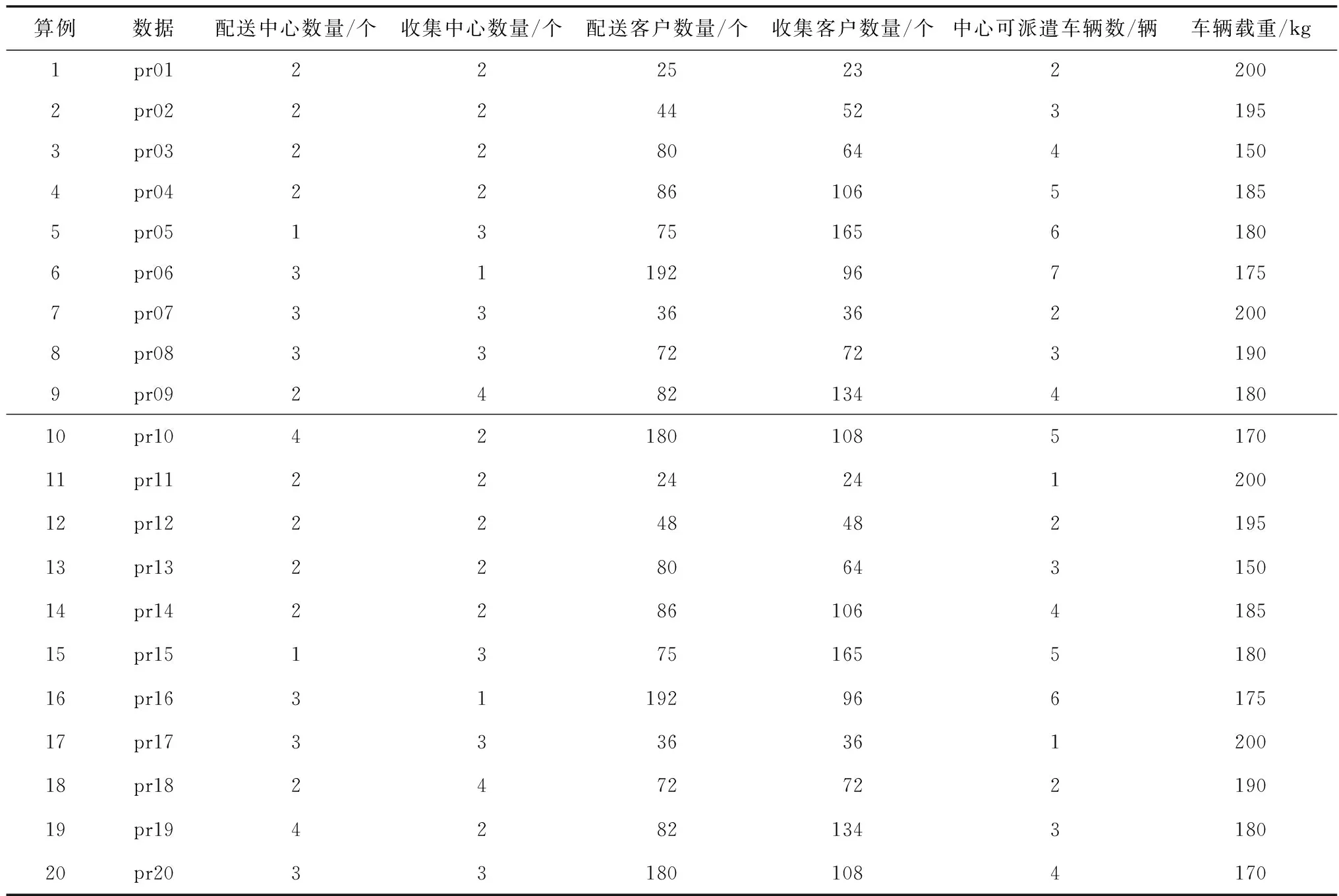
表4 数据集特征Table 4 The characteristics of the data sets

表5 混合算法参数设置Table 5 Parameter setting of the hybrid algorithm

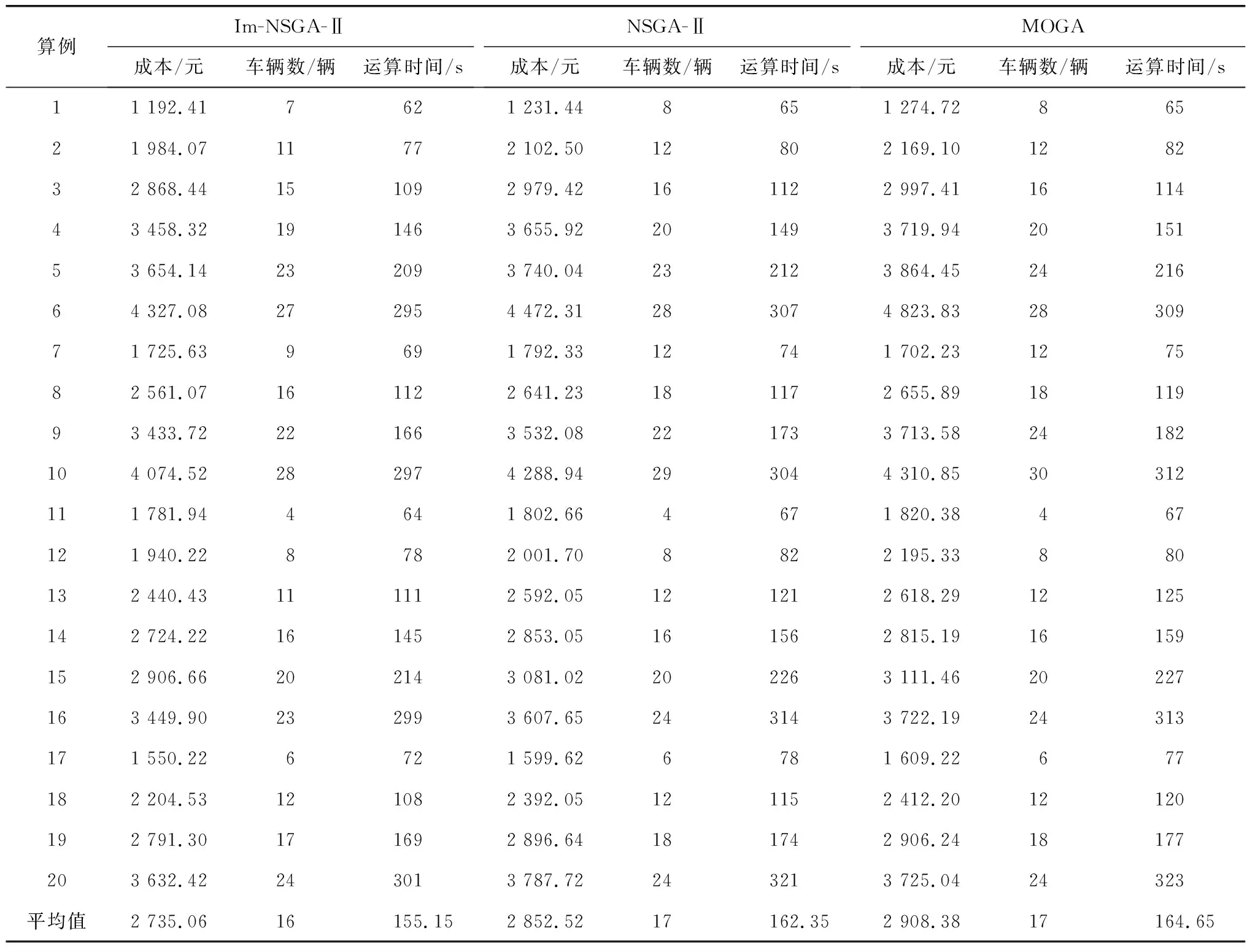
表6 不同算法的计算结果对比Table 6 Calculation results comparison of different algorithms

将Im-NSGA-Ⅱ混合算法与NSGA-Ⅱ和MOGA求解的成本进行t检验和p值检验，得到t检验值分别为-10.004 9和-7.089 91，p值分别为3.14E-09和7.14E-07，由此可知，Im-NSGA-Ⅱ算法与NSGA-Ⅱ和MOGA算法求解得到的成本值结果存在显著性差异。由表6可知，Im-NSGA-Ⅱ混合算法与NSGA-Ⅱ和MOGA求解所得的成本结果存在显著性差异。在成本方面，Im-NSGA-Ⅱ混合算法求解的物流成本平均值为2 735.06元，比NSGA-Ⅱ求解的物流成本平均值2 852.52元降低了4.12%，比MOGA求解的物流成本平均值2 908.38元降低了5.96%；在车辆使用数量方面，Im-NSGA-Ⅱ混合算法求解的车辆使用数量平均值为16辆，低于NSGA-Ⅱ和MOGA求解得到的车辆使用数量；在运算时间方面，Im-NSGA-Ⅱ混合算法的平均运算时间为155.15 s，比 NSGA-Ⅱ的平均运算时间162.35 s节约了7.2 s，比 MOGA的平均运算时间164.65 s节约了9.5 s。结果表明：笔者提出的Im-NSGA-Ⅱ混合算法相对于NSGA-Ⅱ和MOGA具有更好的搜索能力和寻优能力。

4 合作联盟的利润分配

4.1 基于MCRS法的利润分配模型

通过多中心共同配送与收集网络联盟优化，能够节约配送与收集网络运营总成本，节约的运营总成本即为合作联盟可能获得的利润。多中心共同配送与收集网络在线组建合作联盟，由第三方物流平台提供协商等一系列支持，因此联盟A的利润Φ(A)是在第三方物流平台收取δ比例的利润后得到，如式(46)：

Φ(A)=(1-δ)×max{∑r∈AΨ0(r)-Ψ(A),0}

(46)

MCRS方法通常用于研究合作过程中各联盟成员的利润分配问题[7]。根据表2中的相应变量定义，应用MCRS方法计算合作联盟成员的利润分配值，如式(47):

(47)

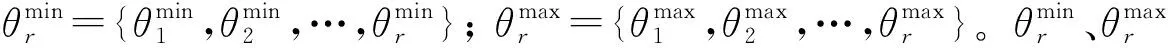
(48)

(49)

s.t.:

φr(A,θ)≥φ0(r) (r∈A)

(50)

(51)

4.2 合作联盟序列选择及稳定性检验

假定稳定的合作联盟构建基于合作联盟形成过程中每个成员获得的利润随着新成员的加入而逐渐增加，因此，利用严格单调路径选择原则[14]对合作联盟建立的序列进行选择。第o个成员加入联盟π时联盟成员r的利润增加百分比如式(52):

(52)

为了进一步加强合作联盟的稳定性，选用合理的利润分配方法能够确保对联盟利润进行公平地分配。根据雪球理论[7]，利润分配方案与核心值之间距离值越小，越能够保证利润分配的合理性，核心值计算公式如式(53):

(53)

5 算例及结果分析

5.1 算例相关数据

笔者以重庆市某企业的物流网络为例进行研究，其中DC1，DC2，DC3表示配送中心，PC1，PC2表示收集中心，C1～C180表示客户点，配送中心、收集中心和客户点的相应地理位置分布如图3。

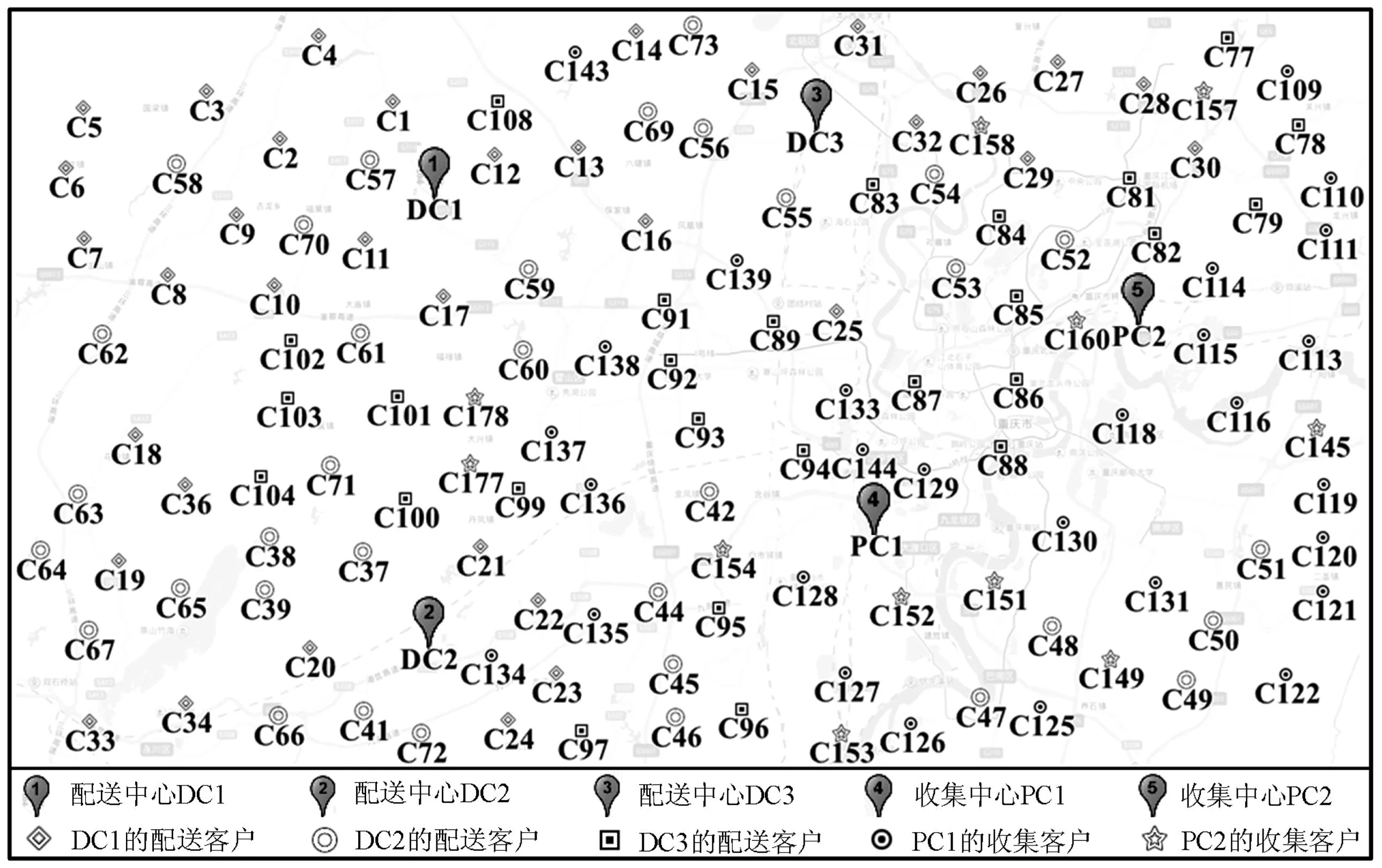
图3 多中心配送与收集网络地理位置分布Fig. 3 Geographical location of multi-center distributionand pickup network

根据已有文献和实际调研[14,23,27]，相应参数设置如下：pop_size=100，γ_max=250，run_max=10，ρsel=0.7，ρcro=0.9，ρmut=0.2，fs=0.106；hs=3.4，fv=0.053，hv=3.9，ue=0.2，ud=0.3，Gs=10 000，Gv=1 000，W=52，F1=800，F2=850，F3=950，F4=700，F5=800，Qs=600，Qv=200，c1=600，c2=650，c3=750，c4=500，c5=600，δ=0.1。

5.2 多中心共同配送与收集网络优化方案

应用MATLAB R2016b软件运用笔者提出的k-means聚类算法计算得到各配送中心与收集中心的服务区域范围，如图4。应用MATLAB R2016b软件运用Im-NSGA-Ⅱ算法计算得到优化后的配送与收集车辆路径，如表7。

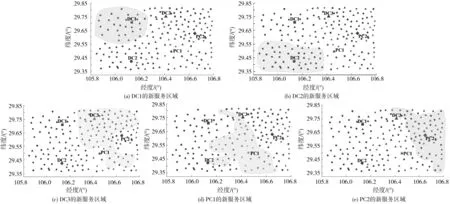
图4 配送中心与收集中心服务区域Fig. 4 The service area of distribution center and pickup center

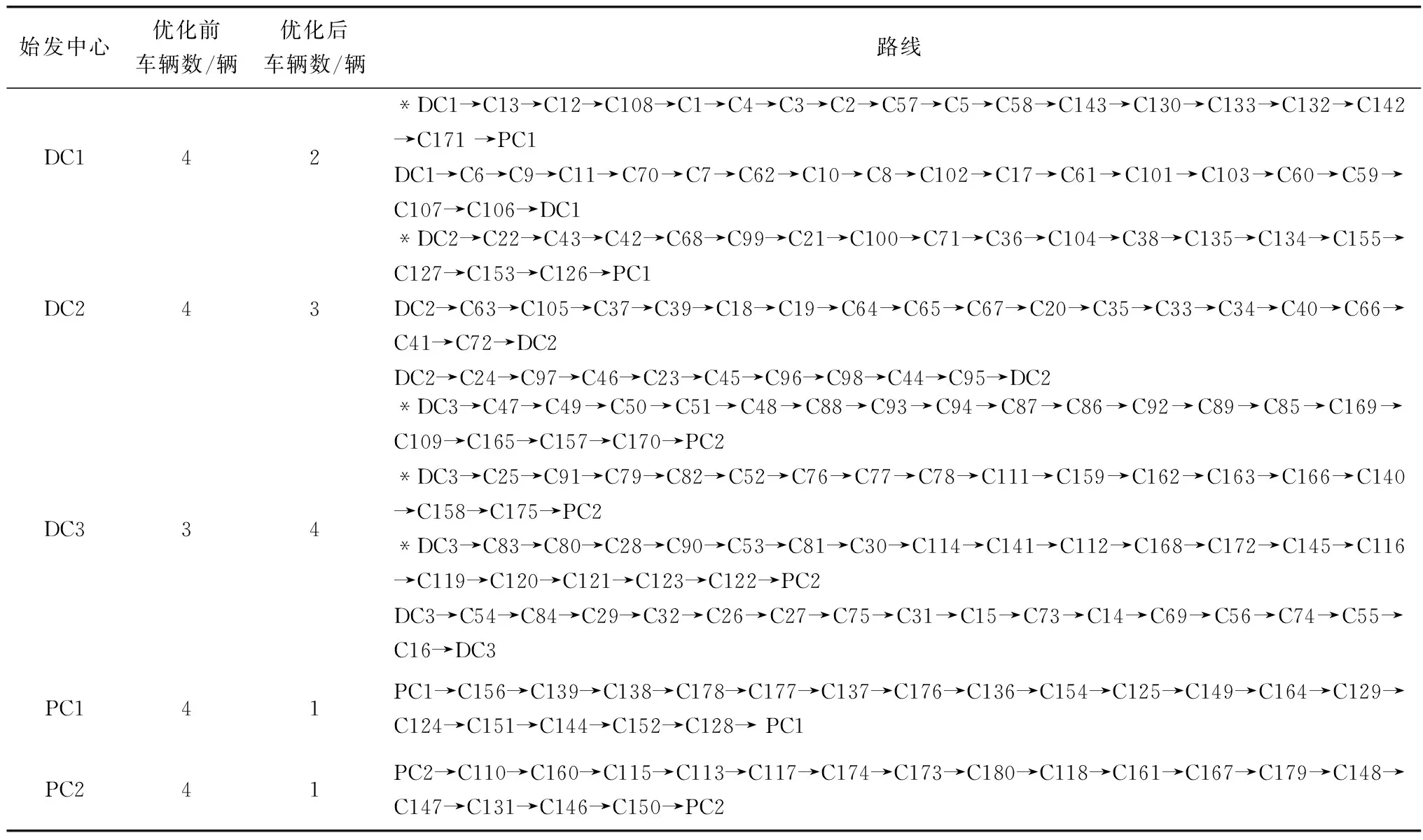
表7 多中心共同配送与收集车辆路径方案Table 7 Vehicle routing schemes of multi-center joint distribution and pickup network

由图4可知，多中心共同配送与收集网络优化方法通过将客户分配给临近的配送中心或收集中心，从而对物流配送与收集服务区域进行合理地划分，有效地减少了原有服务区域重叠的问题。表7中，多中心共同配送与收集网络优化前车辆使用数为19辆，其中DC1使用4辆车，DC2使用4辆车，DC3使用3辆车，PC1使用4辆车，PC2使用4辆车；多中心共同配送与收集网络优化后车辆使用数至11辆，其中DC1使用2辆车，DC2使用3辆车，DC3使用4辆车，PC1使用1辆车，PC2使用1辆车，各配送中心与收集中心使用车辆数均得到了降低。由此可知，多中心共同配送与收集网络优化方法通过对物流配送与收集服务区域内与区域间的车辆路径进行优化，有效地降低了配送与收集车辆使用数。

5.3 多中心共同配送与收集合作联盟

5.3.1 多中心配送与收集合作联盟构建

运用式(47)计算配送与收集合作联盟利润值，并对多中心共同配送与收集网络联盟优化前后的相关成本及车辆使用数进行对比分析，如表8。多中心共同配送与收集网络联盟优化前后的配送成本、收集成本、惩罚成本、运营总成本和配送与收集车辆使用数对比情况如图5。

表8 多中心共同配送与收集网络联盟优化前后对比Table 8 Comparison before and after multi-center joint distribution and pickup alliance optimization

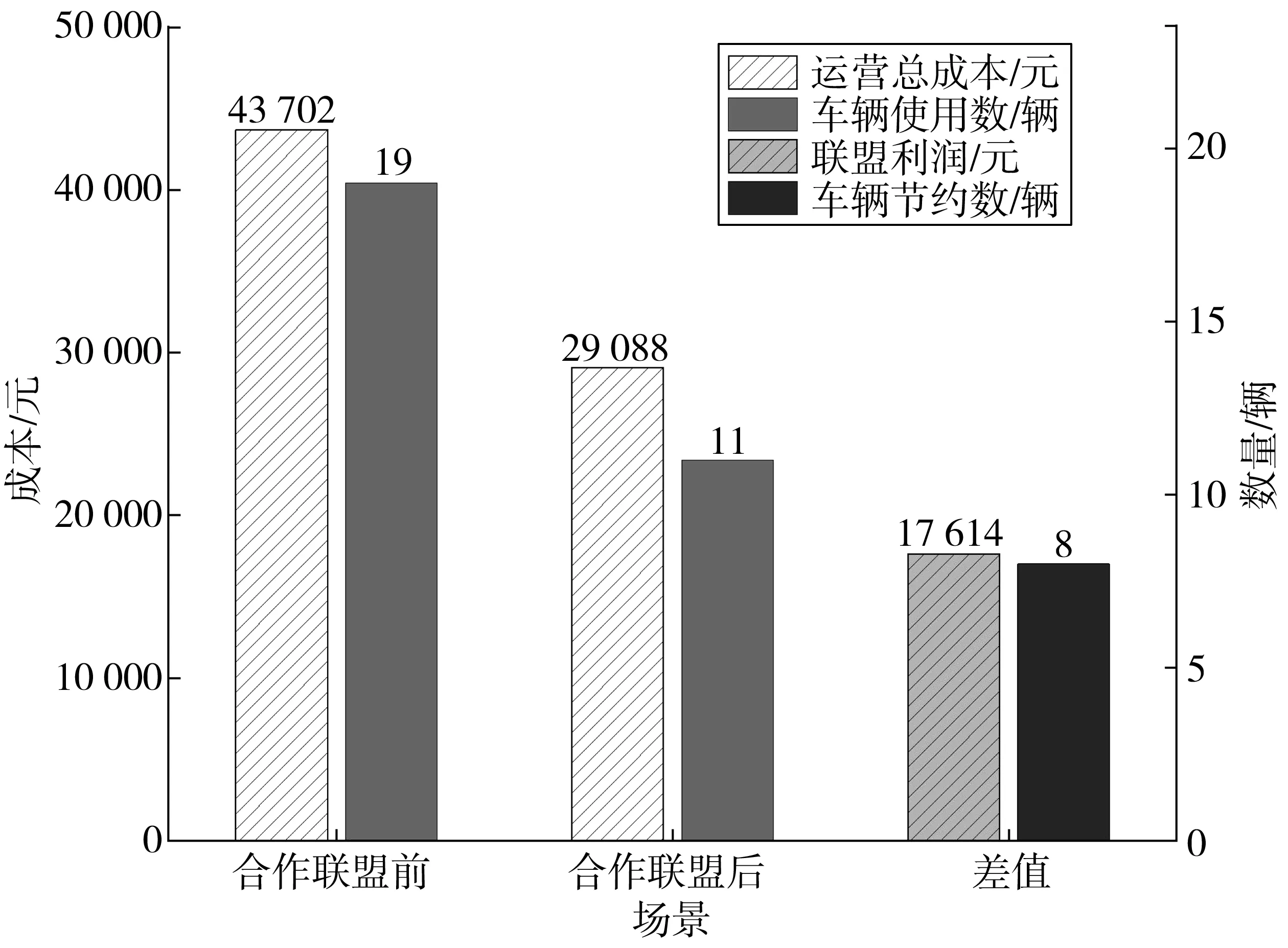
图5 多中心共同配送与收集网络联盟优化前后的运营总成本和车辆使用数对比Fig. 5 Comparison of the total operating cost and the number ofused vehicles before and after multi-center joint distribution andpickup alliance optimization

由表8和图5可知，多中心共同配送与收集网络联盟优化前，网络运营总成本为43 702 元，配送与收集车辆使用数为19辆；多中心共同配送与收集网络联盟优化后，网络运营总成本降低至29 088元，配送与收集车辆使用数减少至11辆。因此，组建合作联盟能够有效地降低网络运营总成本和车辆使用数，同时合理地分配合作联盟所得利润，从而增强合作联盟的稳定性。

5.3.2 多中心配送与收集合作联盟序列选择

利用式(52)计算合作联盟中的每个配送中心与收集中心的利润增加百分比，如图6。当配送中心和收集中心以{PC1,PC2,DC2,DC3,DC1}序列加入合作联盟时，能够确保每个配送中心和收集中心的利润增加百分比随着新联盟成员的加入而严格递增。首先，PC1和PC2合作，PC1的利润增加百分比由13.10% 提高至24.59%；然后，DC2加入合作联盟，PC1的利润增加百分比由24.59% 提高至34.05%，PC2的利润增加百分比由23.58% 提高至35.09%；其次，DC3加入合作联盟，使得PC1的利润增加百分比提高至37.80%，PC2的利润增加百分比提高到37.69%，DC2的利润增加百分比由26.73% 提高至41.10%；最后，DC1加入合作联盟，使得各合作联盟成员利润增加百分比达到40.74%、40.54%、42.46%、40.46%和37.33%。

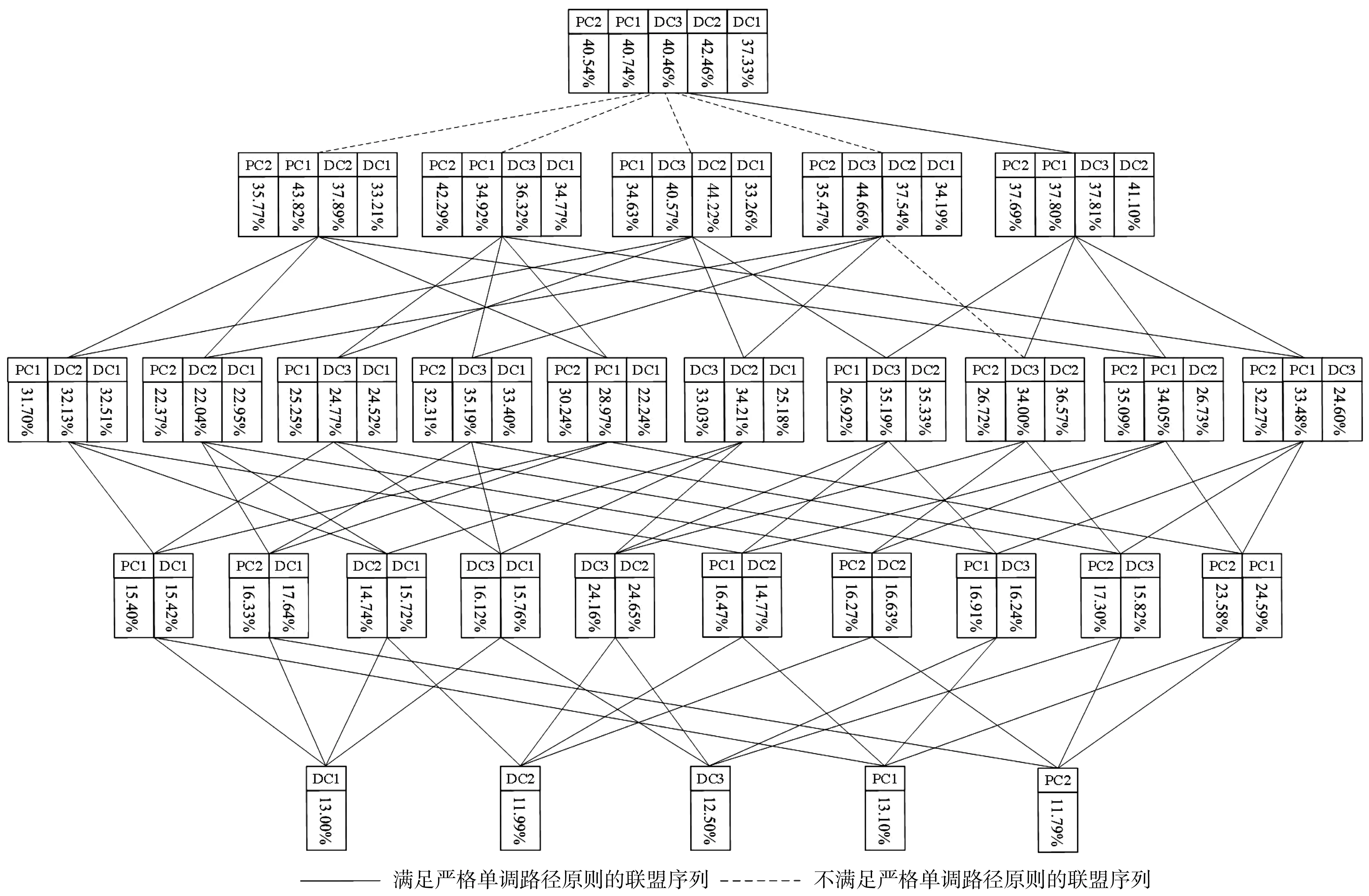
图6 多中心配送与收集合作联盟序列Fig. 6 The sequence of multi-center distribution and pickup collaborative alliances

5.3.3 多中心配送与收集合作联盟稳定性

选用合适的利润分配方法有利于提高合作联盟稳定性。利用式(53)计算得出核心值，并将MCRS、CGA、EPM和Shapley方法计算得出的利润分配方案与核心值进行对比(图7)。由图7可知，MCRS得出的利润分配方案优于CGA、EPM和Shapley方法得出的利润分配方案。

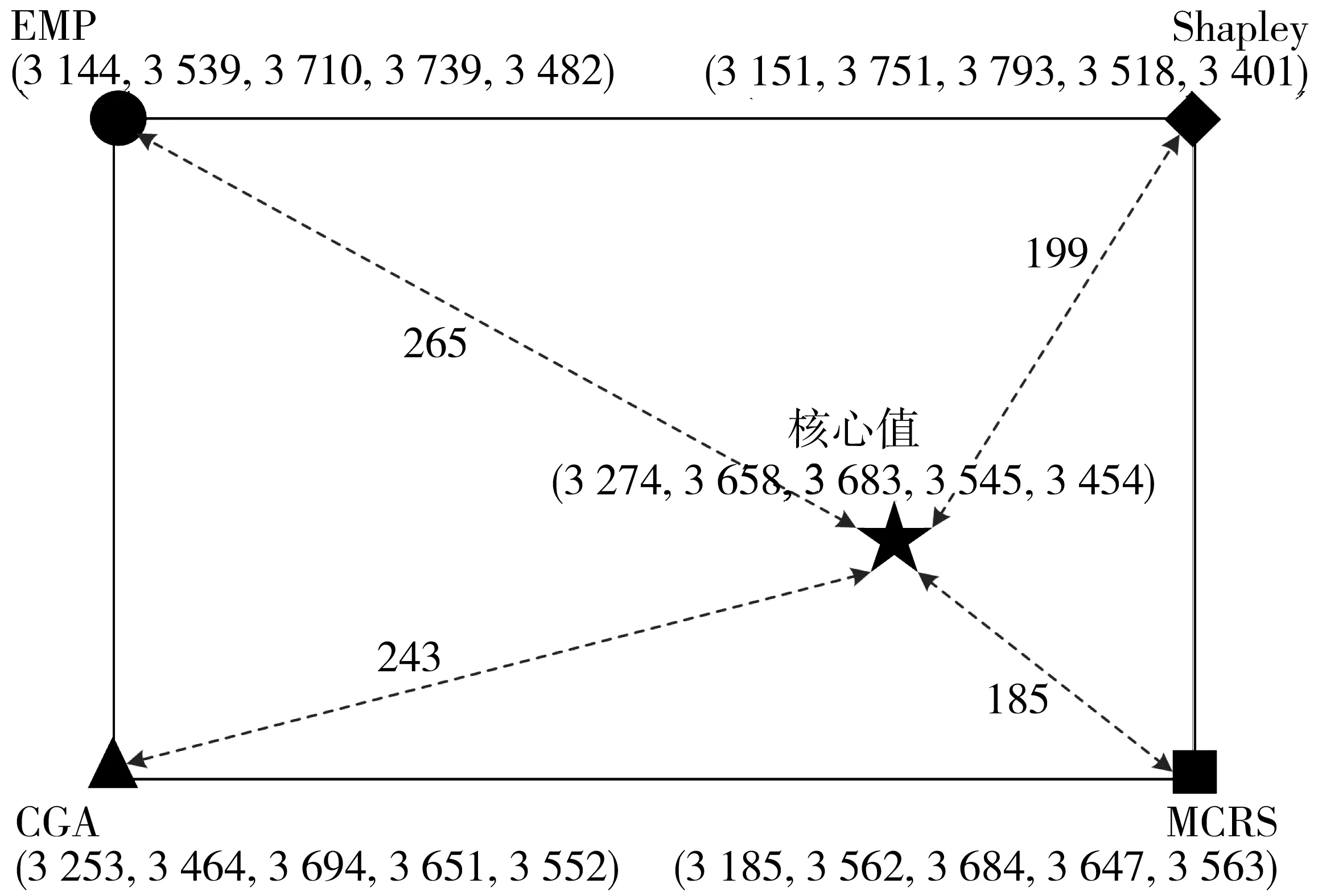
图7 利润分配方案与核心值比较Fig. 7 Comparison of profit allocation scheme and core value

5.3.4 不同合作模式下多中心共同配送与收集网络对比分析

为进一步探讨合作模式对多中心共同配送与收集网络的影响，笔者将合作模式分为仅配送中心共享、仅收集中心共享和多中心共同配送与收集，并对3种不同合作模式下的网络成本和车辆使用数进行对比分析，如图8和表9。

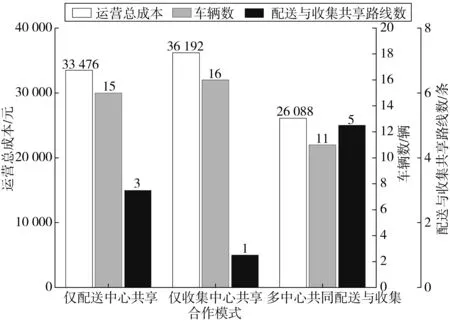
图8 不同合作模式下运营总成本与车辆使用数量对比Fig. 8 Comparison of the total operating cost and the number ofused vehicles based on different cooperation modes

表9 不同合作模式下多中心共同配送与收集网络优化方案比较Table 9 Comparison of multi-center joint distribution and pickup optimization schemes based on different cooperation modes

由图8和表9可知，在运营总成本方面，多中心共同配送与收集模式下的网络运营总成本为26 088元，小于仅配送中心共享模式下的网络运营总成本33 476元及仅收集中心共享模式下的网络运营总成本36 192元；在车辆使用数方面，多中心共同配送与收集模式下的车辆使用数为11辆，小于仅配送中心共享模式下的车辆使用数15辆及仅收集中心共享模式下的车辆使用数16辆。在配送与收集共享路线数方面，多中心共同配送与收集模式下的共享路线数为5条，小于仅配送中心共享模式下的共享路线数3条及仅收集中心共享模式下的共享路线数1条。因此，配送中心与收集中心间的合作更能充分地优化物流资源配置，从而带来更明显的资源整合优势，降低网络运营成本，提高网络运行效率。

6 结 论

笔者针对多中心配送与收集网络联盟优化问题，首先，构建了物流运营总成本最小化和车辆使用数最小化的双目标优化模型；其次，提出了结合k-means聚类算法和Im-NSGA-Ⅱ算法的混合启发式算法，并在Im-NSGA-Ⅱ算法中设计了贪婪算法生成初始可行解和采用精英保留策略提高了算法的寻优能力；然后，将Im-NSGA-Ⅱ混合算法与NSGA-Ⅱ算法和MOGA算法进行了对比分析，验证了笔者所提混合算法的有效性；最后，应用MCRS方法进行多中心配送与收集合作联盟的利润分配研究，按照严格单调路径原则确定联盟最优序列选择过程并与其他方法比较验证了合作联盟稳定性。

以重庆市某企业的配送与收集网络为例，验证了笔者提出的模型和算法的有效性。计算结果表明，优化后的多中心共同配送与收集网络物流运营总成本和车辆使用数分别减少了17 614元和8辆。此外，不同合作模式下的比较结果表明，相对于仅配送中心共享模式，多中心共同配送与收集共享模式物流运营总成本和车辆使用数分别减少了7 388元和4辆，而相对于仅收集中心共享模式，多中心共同配送与收集共享模式物流运营总成本和车辆使用数分别减少了10 104元和5辆。因此，笔者所提模型和算法可用于第三方物流企业进行多中心共同配送与收集网络设计以及多中心合作联盟构建。研究结果可为多中心共同配送与收集优化问题提供新的研究思路，并有利于推动城市智慧物流、共享物流服务模式和数据驱动的物流与供应链可持续发展。