不确定环境下多式联运路径多目标优化

彭 勇，肖云鹏，罗义娟

(重庆交通大学 交通运输学院，重庆 400074)

0 引 言

多式联运是目前最重要的运输组织模式之一，合理的多式联运路径决策，将降低运输成本，提高运输效率。决策目标是影响多式联运路径优化的关键因素，常见的优化目标有最小成本、最短时间、最小风险、最低碳排放等。但过去单一决策目标的研究对运输实践的指导意义较小，因真实情况下决策目标通常是不唯一且相悖的[1]。如货主在运输某些具有强时效性、高附加值的货物(轻工、纺织品及服装、医药制品及鲜活易腐品等)时，通常要求尽快运输交付，但提高运输速度往往意味着运输企业要支出更多的成本[2]。因此选择一条能满足企业经济效益追求，同时能缩短运输时间的最优路径，对于提升企业效益与服务质量，增强企业竞争力具有重要意义。现有研究针对多目标多式联运问题的解决方法有权重法[3]，目标转换为约束[4]，Pareto解[5]等，真实情况下权重法中不同目标权重的确定非常困难，目标转换为约束后增加了算法复杂度且求解质量不高，而Pareto解能很好处理相悖目标之间的表达，而被广泛应用于多目标问题的研究中[6]。

此外多式联运实践因受交通、天气等影响，具有不确定性。现有研究通过随机理论[7]、模糊理论[8]或区间数[9]来处理多式联运路径决策过程中的不确定性。然而忽略了对决策有重要影响的班期[10]，当问题引入班期后，优化目标的分布函数或数值特征通过以上不确定处理方法求解非常困难[11]。而由电脑进行统计抽样实验的蒙特卡洛方法可为各种数学问题提供近似解，尤其针对这种太复杂以至很难分析求解的问题非常有效。

综上，不确定环境下多式联运研究多以单目标函数为主，忽略了现实情况下决策目标的多样性，且现有研究中涉及的不确定处理方法，都不能有效解决多式联运路径决策中有重要影响的班期。故笔者在充分考虑决策人拥有多种互斥目标需求的前提下，针对前人鲜有涉及的班期，构建不确定环境下，考虑班期的以最小成本与最短时间为目标的优化模型。利用蒙特卡洛方法处理模型中时间的不确定性，设计一种将蒙特卡洛仿真与多目标蚁群算法相结合的混合启发式优化求解算法，并改进蚁群算法的转移策略和信息素更新策略，提高算法求解质量。

1 问题描述与建模

1.1 问题描述

图1所示多式联运网络中，节点间的货物运输有多种运输方式供选择，运输时间往往因天气，事故等原因有一定不确定性。不同运输方式在节点处转运将产生转运时间及转运费用。另外，在多式联运中，铁路与水路运输往往按照一定的时刻表(班期)发班，货物难以做到即到即走，而是要等待该运输方式该班发班时刻才能出发，本问题考虑节点处转运不同运输方式有其班期限制这一因素。笔者构建不确定环境下运输总成本最小化及运输总时间最小化的双目标优化模型，求起点到终点的最短路径。

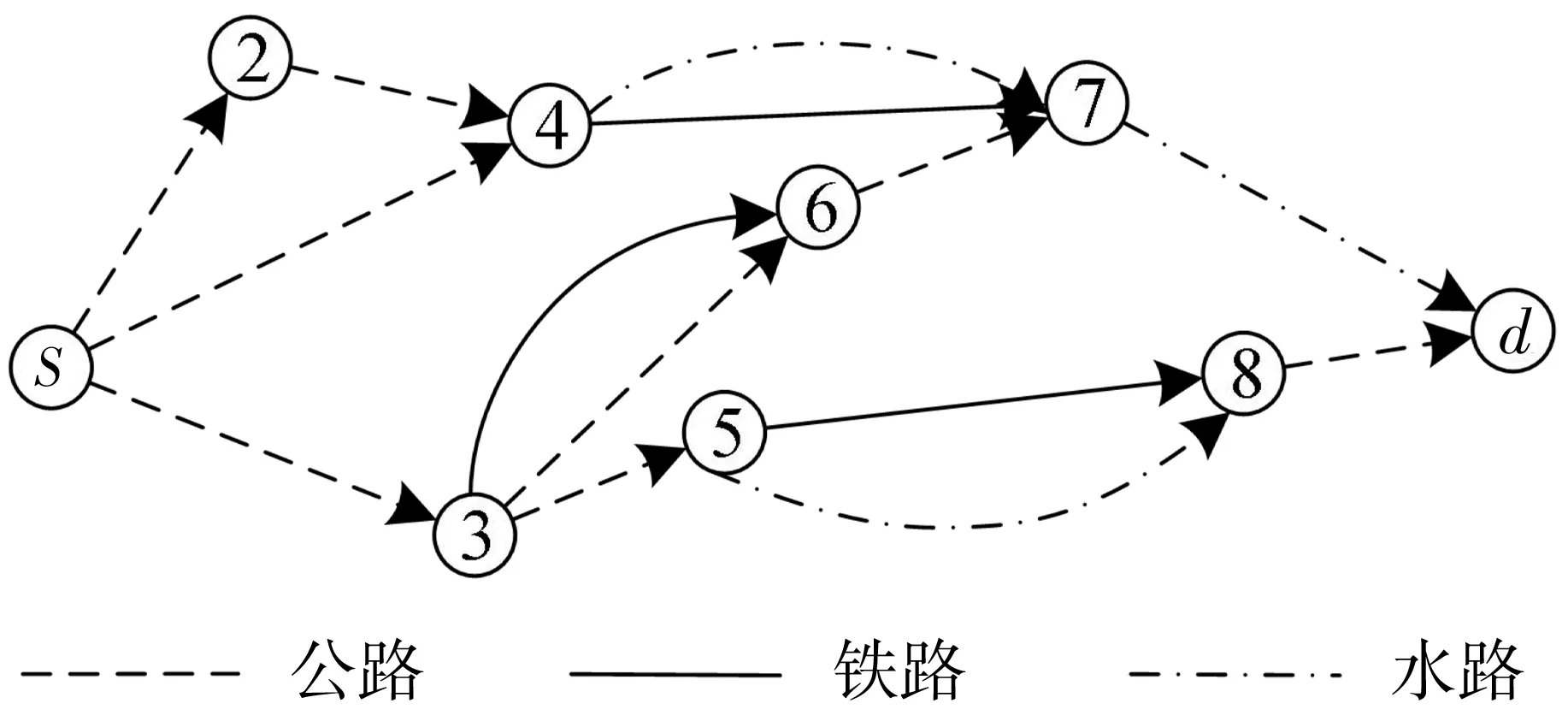
图1 多式联运网络Fig. 1 Multimodal transport network

1.2 模型假设

模型假设如下：①运输货物单一且不可分割；②不同节点间单位运输成本已知；③不同节点间运输时间随机分布已知；④不同运输方式之间的转运时间与成本已知；⑤货物运抵节点若需转运，则立即开始装卸货物；⑥货物在完成转运后按所选运输方式最近班期开始后一行程运输。

1.3 数学模型

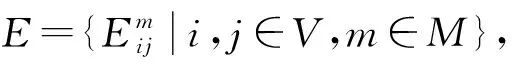
目标函数为：

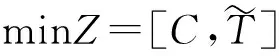
(1)

(2)

(3)

约束条件为：

(4)

(5)

(6)

∀m,n∈M

(7)

(8)

(9)

(10)

(11)

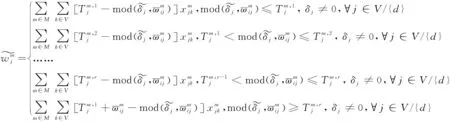
(12)

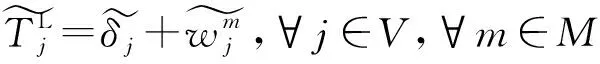
(13)

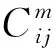
式(1)为目标函数；式(2)为运输总费用；式(3)为运输总时间；式(4)保证路径第一个节点为起点；式(5)保证节点间只选择一种运输方式；式(6)保证单一节点最多发生一次转运服务；式(7)保证转运之后运输方式存在且连续；式(8)保证路径最后一个节点为终点；式(9)保证路径中每个节点的流入边与流出边是唯一且连续的；式(10)为到达节点j的时刻；式(11)为在节点j完成转运的时间；式(12)为在节点j等待运输方式m发车的时间；式(13)为离开节点j的时刻。

2 问题求解

多目标多式联运路径优化问题属于NP难问题，由M. DORIGO等[12]提出的蚁群算法在最短路径问题最优解质量和搜索效率的平衡方面具有较大优势而被广泛应用于解决多目标问题。

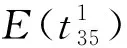
(14)

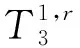
2.1 利用蒙特卡洛方法模拟不确定性

蒙特卡罗方法是利用随机数和概率分布处理不确定和确定性问题的方法，通过给定一定数量的样本，由优化目标的样本平均值估计优化目标真实值，从而求解优化问题。且由“强大数定律”，当优化目标样本数量足够大时，样本平均值为优化目标真实值的无偏估计量。

2.2 改进蚁群算法

在多目标规划中，当解xA的所有目标优于解xB的目标时，称xA支配xB，若无解支配xA，xA为非支配解(Pareto解)。

求解多目标规划的改进蚁群算法信息素更新结合Pareto解，路径信息素由其存留信息与Pareto解对应蚂蚁的信息素决定。路径信息素更新后限制其浓度，避免过早收敛，同时引入方向启发因子，加快迭代速度，改善基本蚁群算法在解决大规模问题时，迭代速度过慢，过早收敛等使算法求解质量低的问题。

2.2.1 多式联运网络编码及参数初始化

将原多式联运网络节点拆分为两部分后组成新节点，新节点的整数位为原节点数，小数位为运输方式编码。初始化蚁群算法相关参数。

2.2.2 蚂蚁移动寻找路径

大量的运输实践经验显示：从起点到终点的最短路径中任一路段与“起点-终点”连线间的夹角通常较小，即，最短路径方向总是循着目的地方向，具体如图2。即下一备选路径与“起点-终点”连线间的夹角的大小与其成为最短路的概率呈负相关关系。

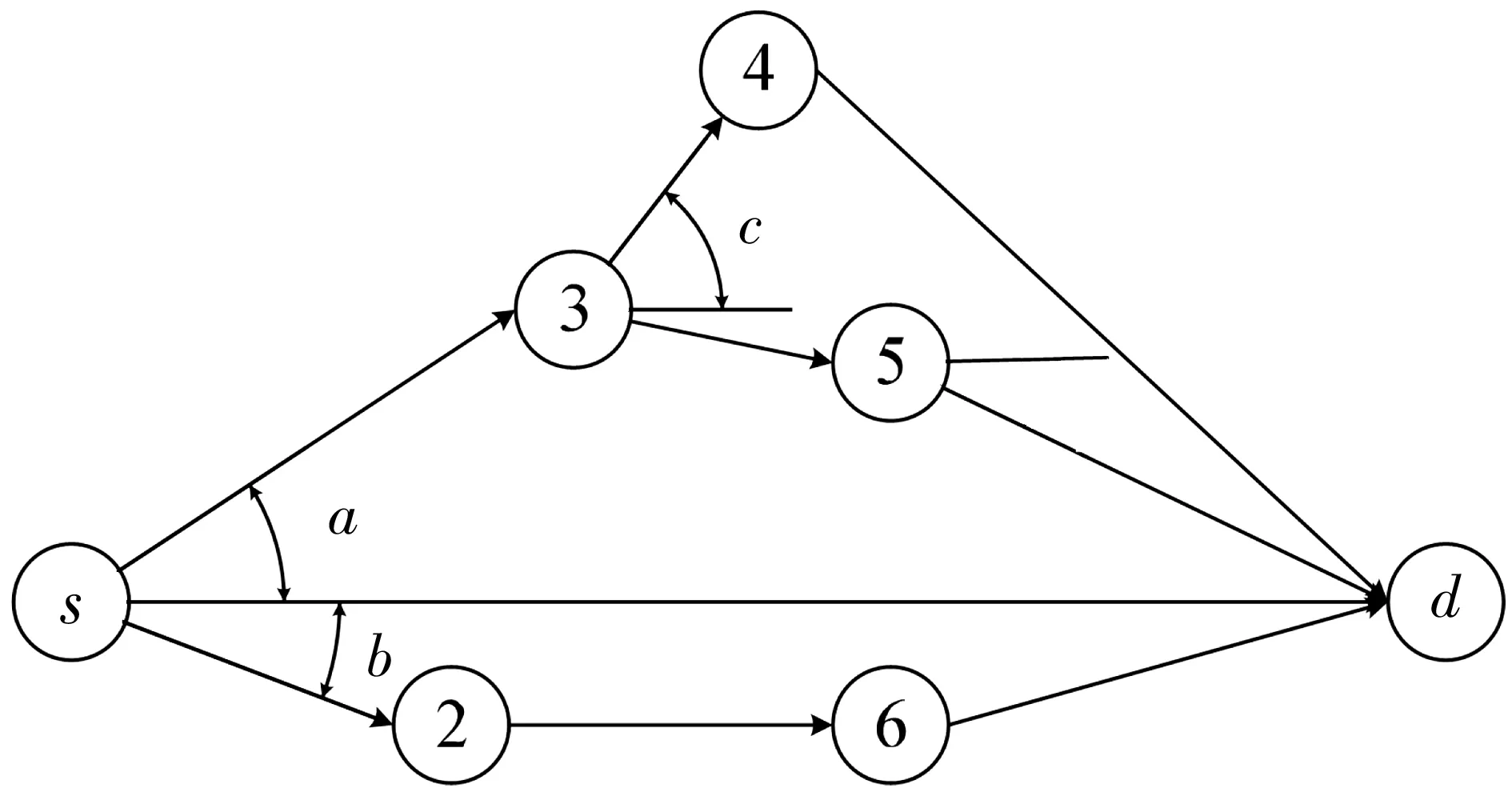
图2 路段方向夹角示意Fig. 2 Schematic diagram of the angle of road section direction

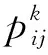
(15)

(16)

式中：γ为节点i,j间的路段和“起点-终点”连线间的夹角，夹角越小，φij越大，其为最短路径与选择该路径的概率就越大；τij,α分别为为节点i,j间的信息素浓度及其启发因子；ηij,β分别为为节点i,j间的能见度及其启发因子；allowedk是蚂蚁下一步可选择路径的集合。

每只蚂蚁从起点出发，首先确定下一节点的可行路径并保存入allowedk中；若allowedk为空集，蚂蚁返回起点，重新开始选择路径；否则根据式(16)确定的转移概率与轮盘赌，选择下一个节点，直至蚂蚁到达终点，蚂蚁完成一次路径。

2.2.3 蒙特卡洛仿真

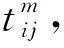
2.2.4 求Pareto解

运用快速非支配排序算法[14]求截至本次迭代所有可行解的Pareto解。

2.2.5 信息素更新

对Pareto解路径中节点i,j间路段更新信息素τij，更新策略为：

τij(u+1)=(1-ρ)×τij(u)+ρ×Δτij(u+1)

(17)

(18)

式中：τij(u)为第u次迭代，路段i,j上的信息素值；τij(u+1)为更新后的信息素值；Δτij(u+1)为信息素增量；L(u)为第u次迭代Pareto解中可行解的平均值；ρ为信息素挥发系数。

为避免“过早收敛”，通过“最大-最小蚂蚁系统”限制路段信息素。

τij(u+1)∈[τmin,τmax]

(19)

(20)

(21)

式中：Vn为节点总数；θbest为选取最优的概率；h(u)为第u次迭代Pareto解中各组可行解平均值的最小值。

3 算例分析

选取文献[15]的公铁海联运实例，实例中包含25个节点，构建以朔州为起点，上海为终点的多式联运网络。假设不同节点同一运输方式班期相同，不同运输方式班期如表1，公路运输时间在±20%之间波动，铁路与水运运输时间在±10%之间波动。

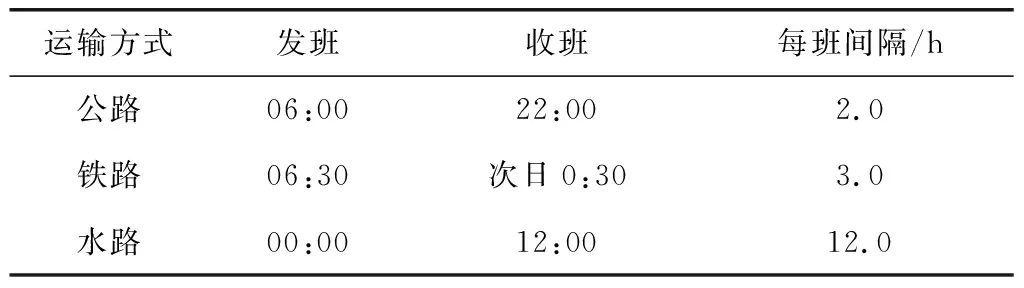
表1 不同运输方式班期Table 1 Schedule of different transportation modes

3.1 算法对比

多目标优化解的质量常用比较指标有Pareto解的均匀性(SP)及其宽广性(MS)。

SP定义为：

(22)

(23)

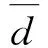
MS定义为：

MS=

(24)

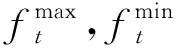
蚁群算法参数设置为：蚂蚁数量取20、迭代次数取20次，蒙特卡洛模拟次数K=1 000，α=0.8，β=0.2，ρ=0.3，货物重1 t。将改进蚁群算法、方向蚁群算法、信息素限制蚁群算法及基本蚁群算法，分别运行50次，结果如表2。

结果显示，方向蚁群算法的解集平均值优于基本蚁群算法与信息素限制蚁群算法11%～25%，说明方向启发因子能够加快迭代速度；Pn低24%～57%表明其易过早收敛，无法为决策提供更多选择。相反，信息素限制蚁群算法能找到更多的Pareto解，但是解的质量不高。结合表2与图3～图6，同时考虑两种策略的改进蚁群算法能在考虑Pn同时兼顾解的质量，相较其他算法有一定优越性。

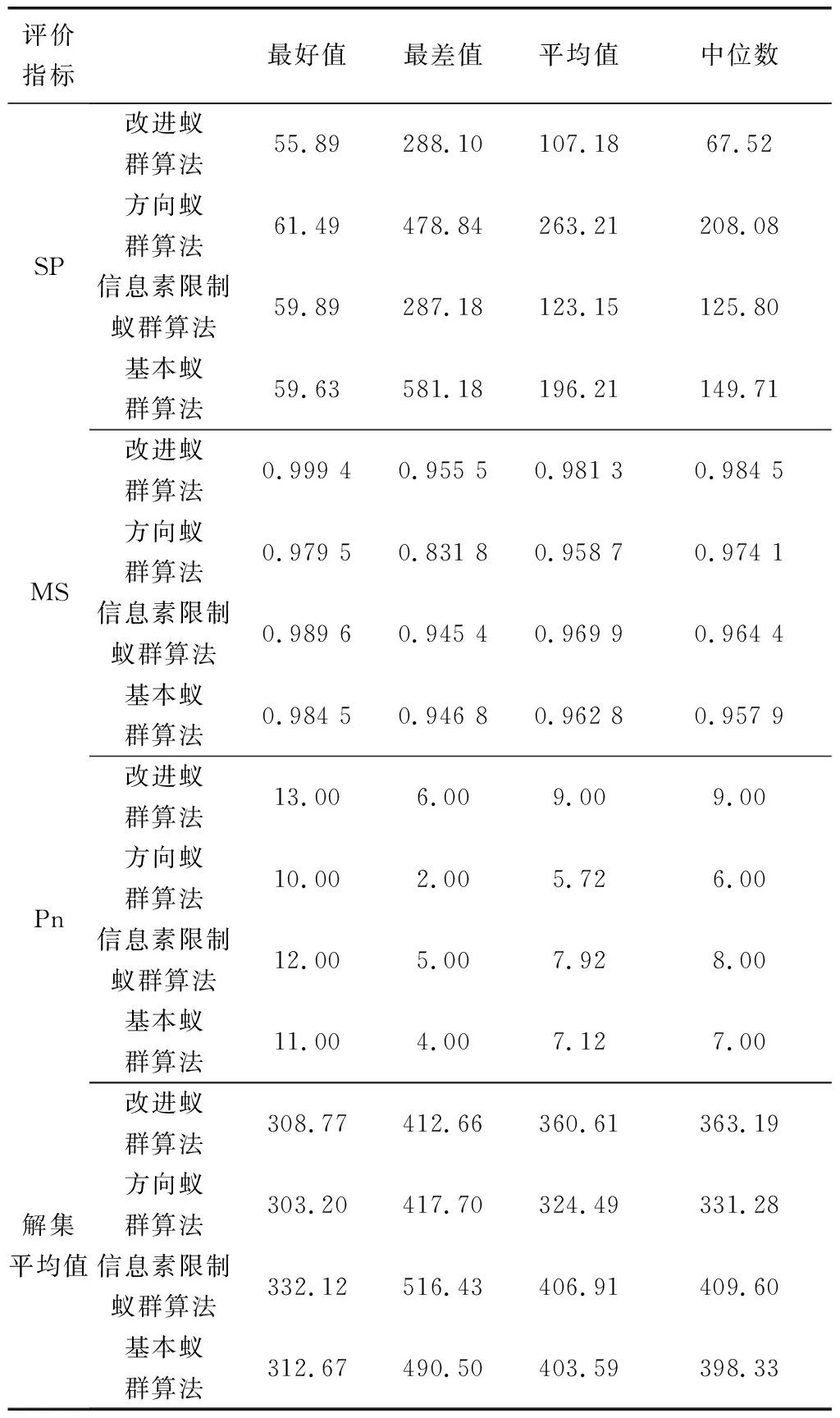
表2 算法运行结果对比Table 2 Comparison of algorithm running results

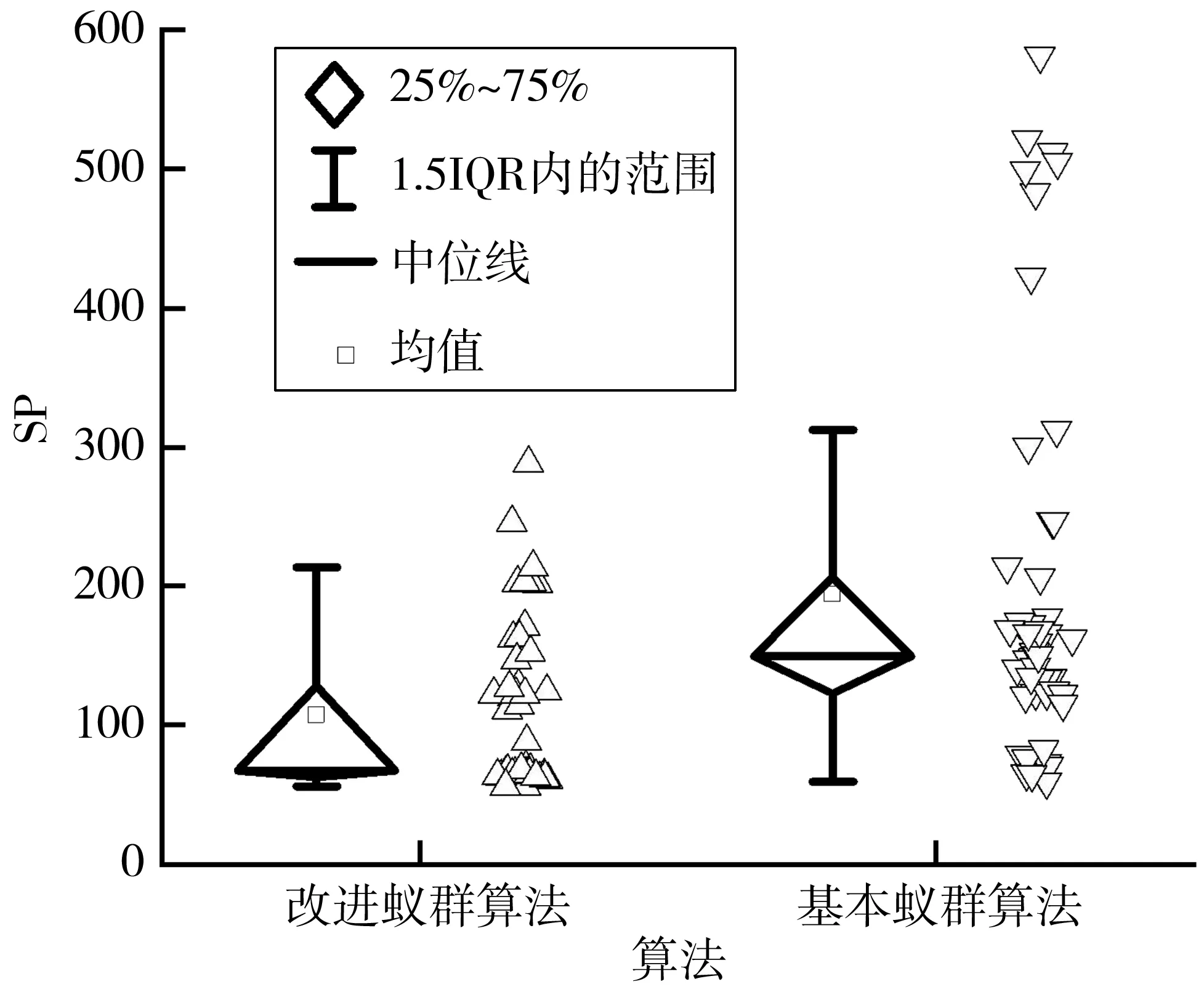
图3 SP对比箱图基本蚁群算法Fig. 3 SP comparison box plot of basic ant colony algorithm

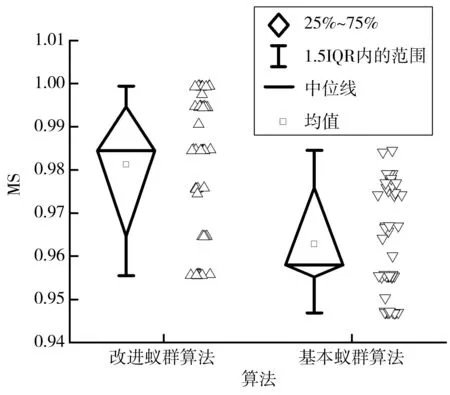
图4 MS对比箱Fig. 4 MS comparison box plot

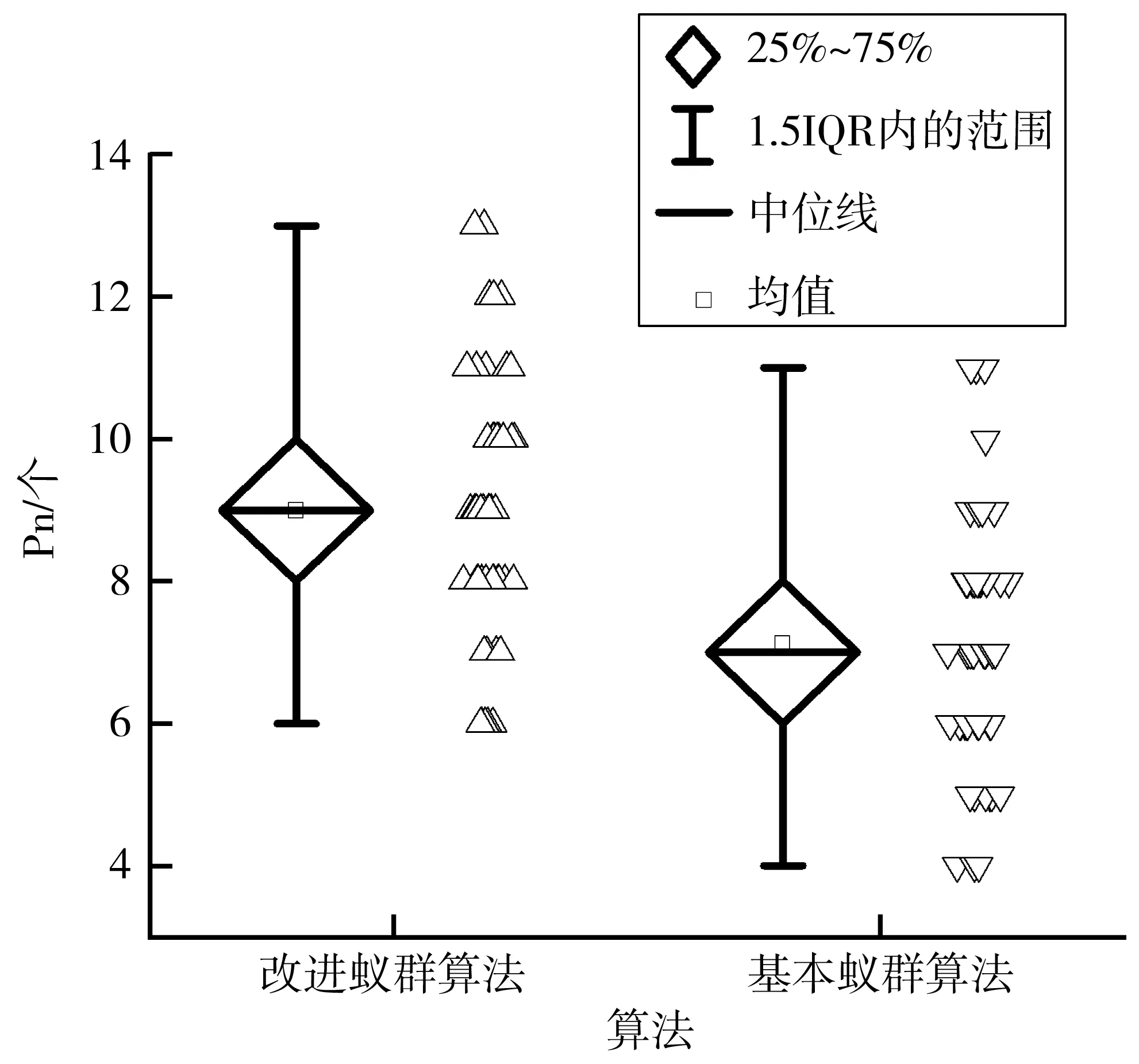
图5 Pn对比箱Fig. 5 Pn comparison box plot

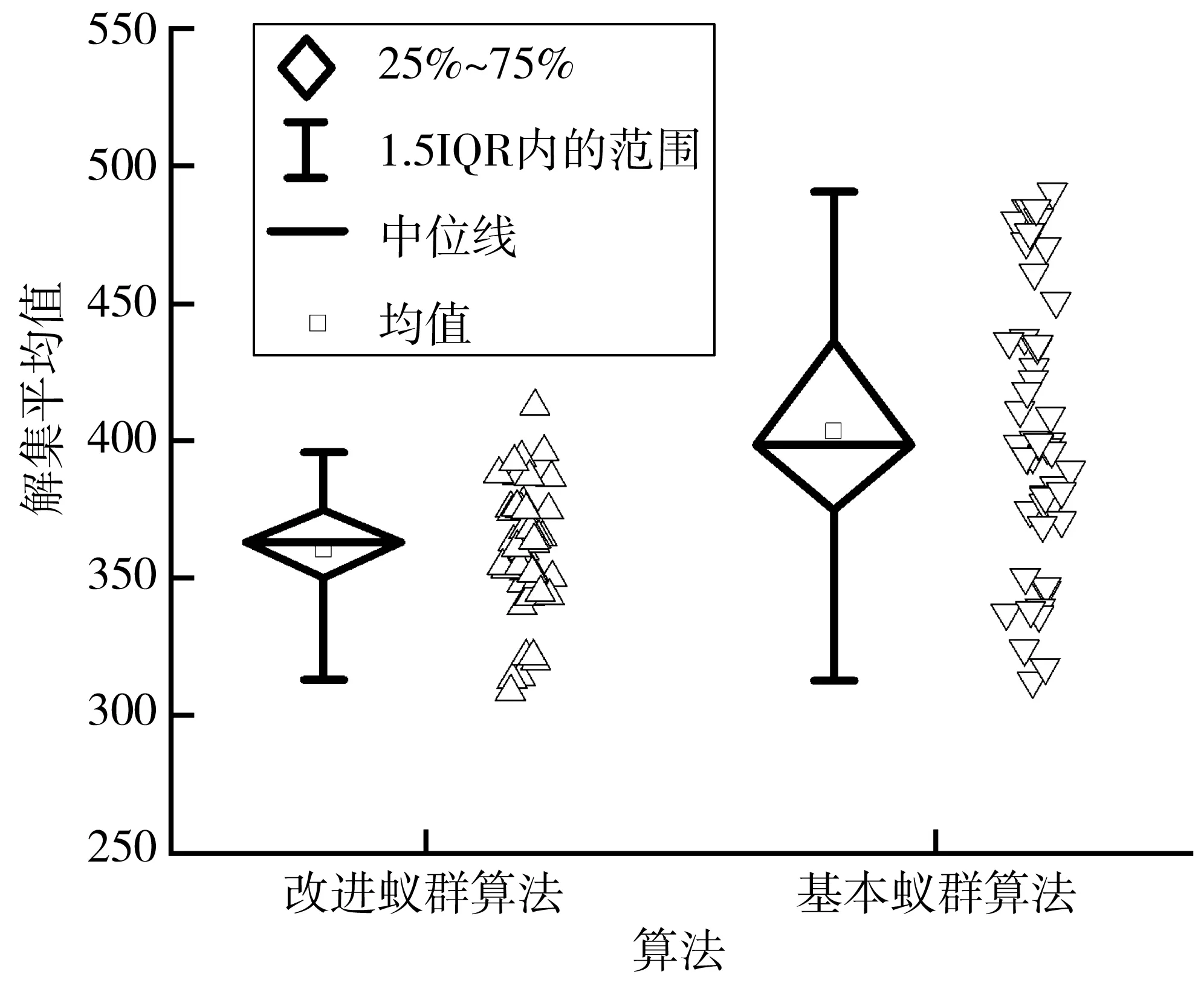
图6 解集平均值对比箱Fig. 6 Solution set mean comparison box plot

3.2 算法参数分析

蚂蚁个数设20，最大迭代次数30，α取0.7～0.9，β取0.3～0.1、ρ取0.2～0.4，其他参数不变，进行50组对比实验。结果如图7，仅α=0.9，β=0.1，ρ=0.4时，实验平均Pn波动超过1；实验平均解集平均值整体波动小于5%。

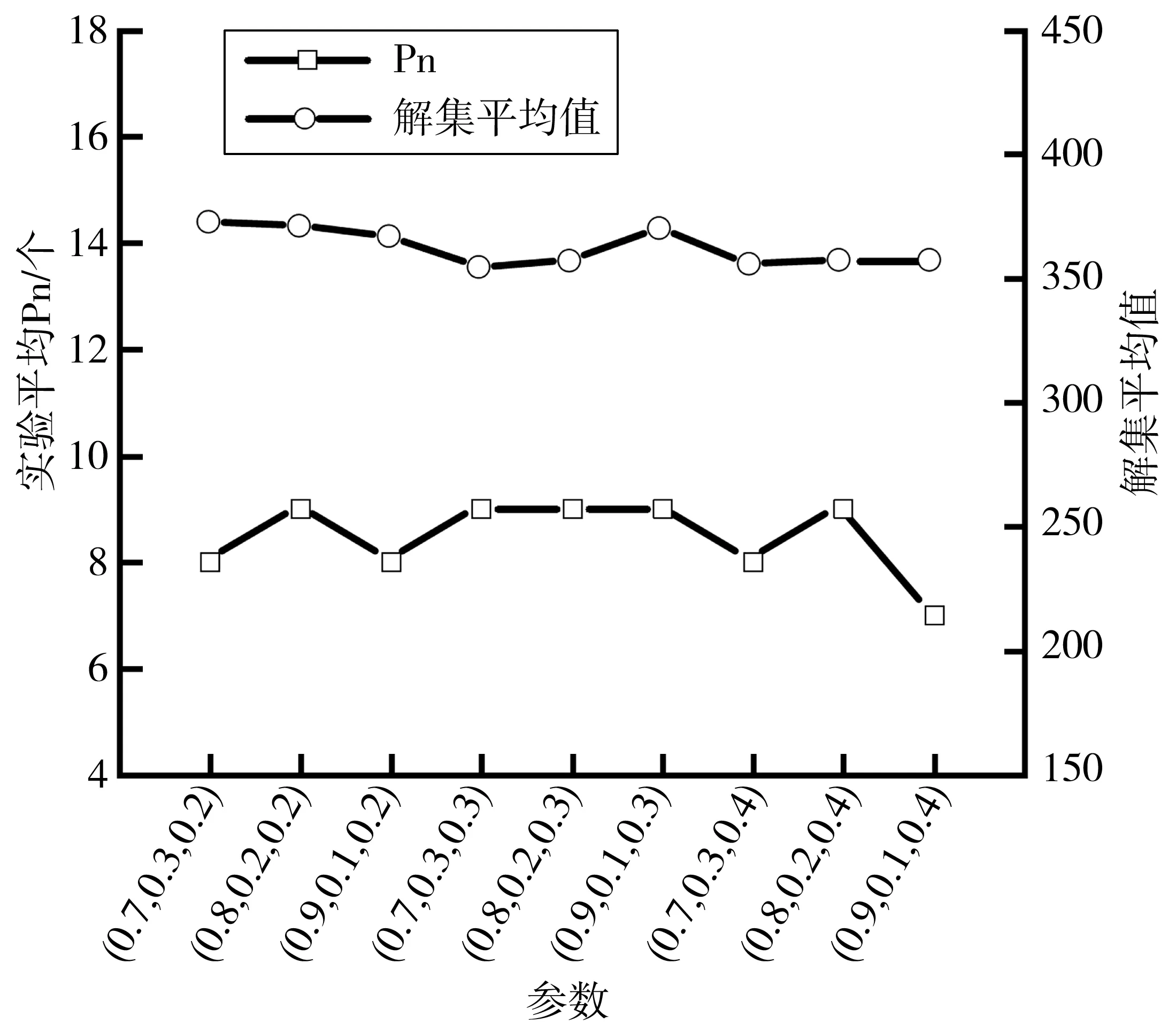
图7 不同参数组合实验平均Pn与解集平均值Fig. 7 Experimental mean Pn and solution set mean of differentparameter combinations

设最大迭代次数30次，其他参数不变，蚂蚁数分别为10、15、20和25进行了50组对比实验。结果如图8～图9，不同蚂蚁数算法都能在较低的迭代次数使实验平均Pn与解集平均值趋于定值；迭代结束实验平均Pn接近统一，实验平均解集平均值波动小于5%。以上结果表明改进蚁群算法对参数设置要求较低，算法具有一定的鲁棒性。

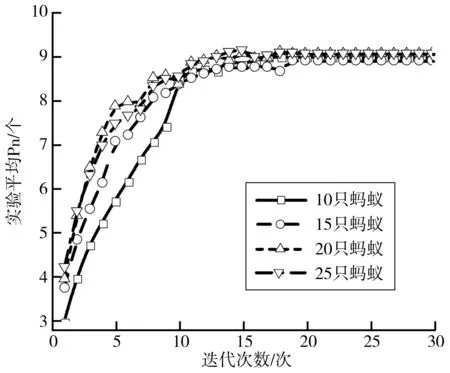
图8 迭代次数与蚂蚁数对实验平均Pn的影响Fig. 8 The influence of the number of iterations and ants on theexperimental mean Pn

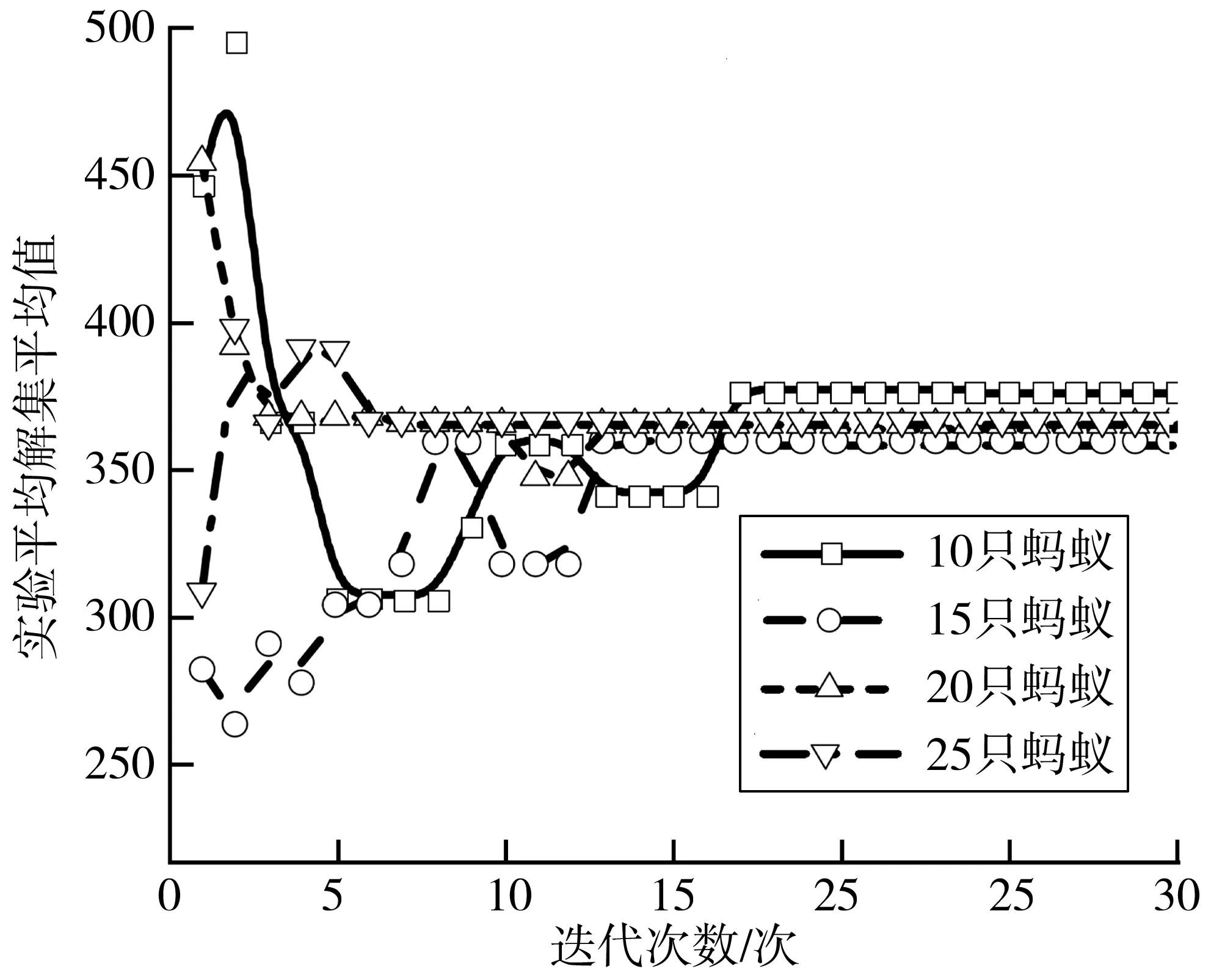
图9 迭代次数与蚂蚁数对实验平均解集平均值的影响Fig. 9 The influence of the number of iterations and ants onthe average value of experimental mean solution set

3.3 Pareto解分析

取算例结果中部分Pareto解如表3，决策人可根据对成本与时间的敏感性挑选不同方案。

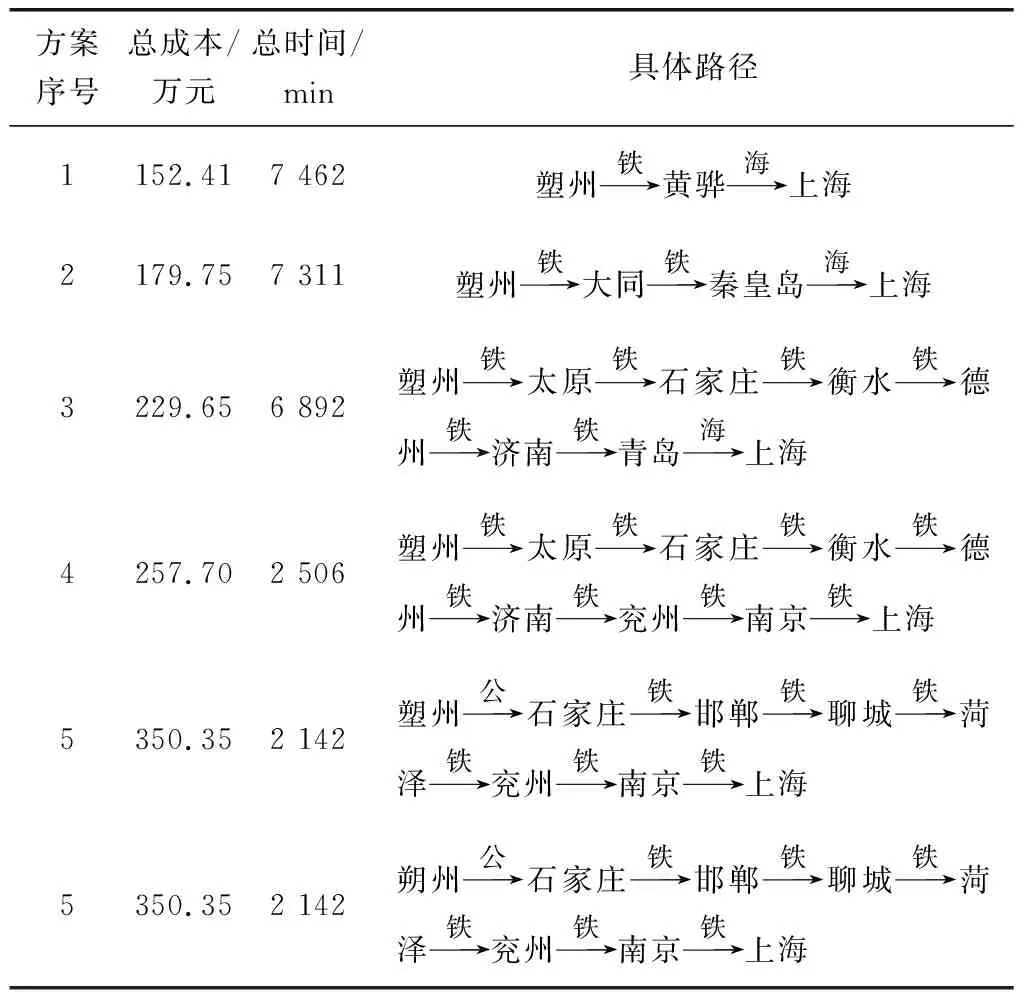
表3 部分非支配的运输方案Table 3 Partially non-dominant transportation scheme

将基于权重和基于Pareto理论的蚁群算法进行比较，C和T两个优化目标通过权重转化为minZ=ω1C+ω2T单目标，其中ω1和ω1为权重，通过调整权重比例得到如表4。

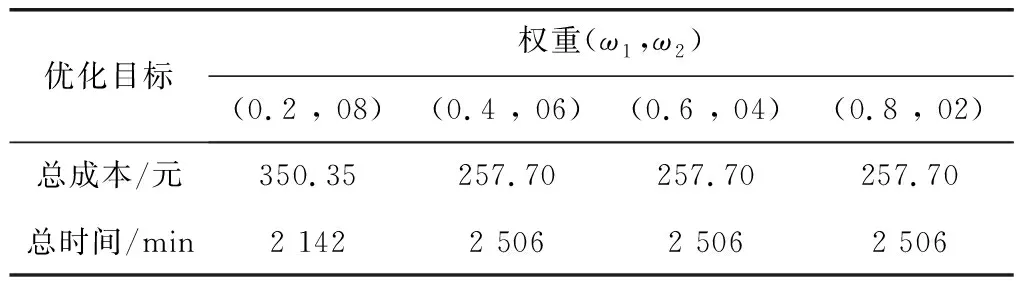
表4 不同权重下运输方案Table 4 Transportation schemes under different weights

通过图10可知，Pareto解比基于权重的双目标蚁群算法的求解结果好，能提供更多可行方案，表明Pareto方法能更好地处理双目标问题。

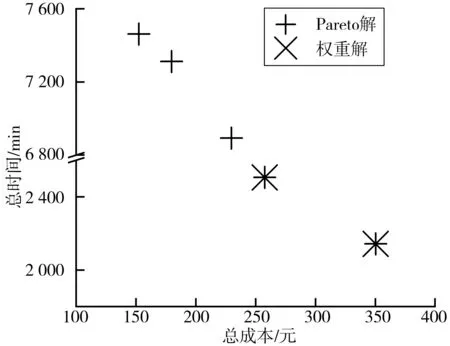
图10 Pareto解与权重解对比Fig. 10 Comparison of Pareto solution and weighted solution

4 结 语

以运输总成本与运输总时间为优化目标，构建不确定环境下的多式联运最短路径模型。使用蒙特卡洛方法处理网络中的不确定性，改进基本蚁群算法的转移策略和信息素更新策略，结合非支配排序的改进蚁群算法求解Pareto解。同一环境下进行50次试验，验证改进蚁群算法优化效果；然后分别改变迭代次数、蚂蚁数量、信息素启发因子、能见度启发系数和信息素挥发系数，结果显示：算法参数设置对算法影响不明显；同时算法结果验证了Pareto理论解决多目标问题的优越性。

通过对一个仿真算例进行实验分析。研究发现公路运输拥有较高灵活度，能提高货物运输效率，但运输成本较高；铁路运输各属性平衡；海运运输将大幅度提升运输总时间，但成本较低。故当决策人对货物无时效性要求，且对成本比较敏感，可选择方案1或2，通过海运运输，牺牲运输时间，降低运输成本；如决策人对货物时效性(如原材料限制后续生产)及成本皆有要求，可根据决策人实际要求选择合适方案；如决策人对货物时效性有要求，且愿意提高预算，可选择方案5，在运输路径中部分选择公路运输，提高运输效率。