分数布朗运动干扰下广义模糊系统的有限时间随机有界性分析
2021-11-09刘铭宇
刘铭宇,解 静,李 明
(青岛理工大学 信息与控制工程学院,青岛 266525)
在实际的工业生产中,存在着大量时变、时滞、非线性等问题。工程师利用各种方法简化系统动态很难达到控制目的,因此复杂的控制过程通常是由实践经验丰富的技术专家现场操控和识别。这一现象表明传统控制理论对于过于复杂或者难以精确描述的系统无法发挥有效作用,因此便诞生了以模糊数学、逻辑关系和逻辑推理等理论为依据的模糊控制理论。1985年日本学者Takai T和Sugeno M首次提出T-S模糊控制系统。这个系统特点是将非线性与线性之间建立起一种联系,可以用线性系统的方法来处理非线性模糊系统。经过多年的发展,模糊控制技术的应用已涉及图像识别、军事、化工、宇航飞天、国民经济等众多领域。
广义系统是由微分方程和代数方程的混合形式表示的,不仅包含正常系统中的指数解,还含有正常系统所不具有的脉冲和动态解。而且由于广义系统的参数矩阵E是不满秩的,正常系统是满秩的,正常系统可以看作广义系统的一个特例。不难看出,相较于正常系统广义系统能够更精确地描述物理系统,如电网系统、化工过程、核反应系统等。
在现实环境中存在着各种各样的随机因素,这些随机因素可能会破坏被研究系统的稳定性,因此研究随机扰动的控制问题具有重要意义。HU等[1]研究了分数阶噪声驱动的线性系统的随机控制。WANG等[2]通过衰减增益控制器解决了带有测量噪声的质量均方包容控制问题,其中测量噪声采用标准布朗运动建模。标准布朗运动是一个独立的增量过程,但在一些实际情况下许多现象具有记忆性。研究发现:分数布朗运动是一类带有Hurst指数H∈(0,1)的特殊高斯随机过程,当Hurst指数取值为H∈(1/2,1)时,分数布朗运动将具备样本路径连续性和长记忆性的特点。因此,分数布朗运动可以更好地用于描述现实社会和自然界许多现象的本质属性,例如图像纹理分析,交通流,智能电网,脑功能信号分析等。因此本文主要讨论Hurst指数取值为H∈(1/2,1)时分数布朗运动驱动的随机微分系统的稳定性。
近年来,分数布朗运动在动力学系统中产生的随机扰动现象开始引起部分学者的关注,文献[3-5]给出了带有分数布朗运动的随机方程的一些基本性质。文献[6]给出了具有分数布朗运动的随机延迟微分方程的解。CHEN[7]用分数布朗运动研究了随机方程的近似能控性,即系统可以被导向到任意小的终态邻域;ZHOU等[8]对分数布朗运动驱动的滞后神经网络稳定性进行了分析;LU等[9]研究了分数布朗运动干扰下线性系统的鲁棒H∞滤波,等等[10-11]。目前,关于分数布朗运动对广义模糊系统稳定性的影响问题的研究还较少,因此本文致力于讨论分数布朗运动干扰下的广义模糊系统的反馈控制和广义有限时间随机有界性问题。本文的主要贡献是给出了模糊状态的反馈控制器,并利用线性矩阵不等式得到系统有限时间随机有界的一些充分条件。
1 系统描述及准备知识
考虑一个带有分数布朗运动的广义模糊系统,它由一个T-S模糊模型近似。设该广义模糊系统的第i条规则为
Plant Rulei:

THEN

(1)

通过模糊混合,上述模糊模型(1)可变换为
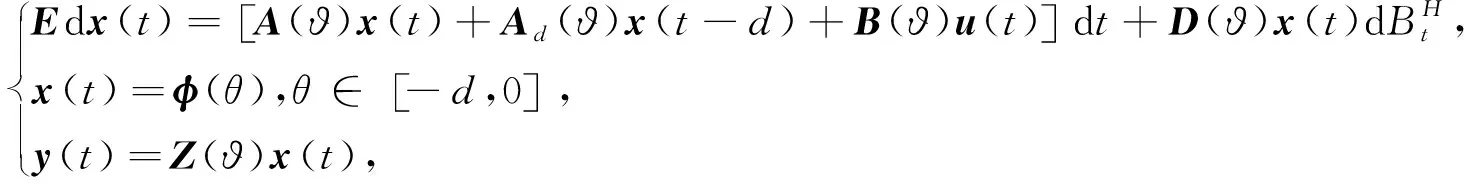
(2)



定义1[12]:给定时间区间[0,Tf],常数c1>0,c2>0,且c2>c1,对称正定矩阵P>0。如果具有分数布朗运动的广义随机系统(2)是正则、无脉冲且满足
Em{xT(0)ETPEx(0)}≤c1,⟹Em{xT(Tf)ETPEx(Tf)}≤c2,
其中Em表示数学期望,则称系统(2)关于参数(c1,c2,[0,Tf],P)是有限时间随机有界的。
定义2[13]:设μ(r)是一个非连续非递减函数,μ(0)=0,且当r>0时μ(r)>0。对于h>0,设Sh={x∈Rn:|h| V(t,0)=0,V(t,x)≥(μ|x|), Vx(t,x)Cx(t)∈L(0,T), 并使得LHV(t,x)≤0成立,则系统(2)随机稳定。 定义3[14]:假设带有分数布朗运动的广义随机微分系统: 并且V(t,x)的随机微分为 式中:φ(s,t)=H(2H-1)|s-t|2H-2。 采用并行分布式补偿方案,为具有分数布朗运动的广义模糊系统(2)设计如下的模式相关的T-S模糊反馈控制器: Plant Rulei: THEN u(t)=Cix(t),i∈T, (3) 其中Ci∈Rq×n是待确定的状态反馈增益矩阵。那么,通过模糊混合得到总体模糊控制器如下: u(t)=C(ϑ)x(t), (4) 将模糊控制器(4)代入系统(2),可得广义模糊闭环动态系统为 (5) ETP=PE≥0, (6) (7) (8) 证明:为了处理分数布朗运动对系统随机稳定性的影响,在时间区间[0,Tf]上定义如下与Hurst指数相关的新型Lyapunov泛函: (9) VxD(ϑ)x(t)=2xT(t)ETPD(ϑ)x(t)∈L(0,T)。 (10) 然后根据随机微分公式有 (11) (12) 式中:ζT(t)=[xT(t),xT(t-τ(t)),xT(t-d)]; 根据Schur补引理可知,Γ≤0等价于定理1中条件(7)成立。由于在时间区间[0,Tf]内有下列不等式成立 (13) 将式(7)(12)和(13)代入式(11),可以得到: (14) 其中, (15) (16) 进一步地,在LHV(t)<0成立的结果下,一定存在常数α1>0使得 LHV(t)<α1V(t),t∈[0,Tf] (17) 对式(17)两边从0到t(t∈[0,Tf])积分并求均值可得 (18) 再利用Gronwall不等式可得Em{V(t)} Em{V(t)}≥Em{xT(t)ETPx(t)} (19) 且 (20) 其中c1=Em{xT(0)ETPEx(0)},将式(19)和(20)代入式(18),有 Em{xT(t)ETPEx(t)}≤c2 (21) 综上, 根据定义1可得系统(5)关于(c1,c2,[0,Tf],P)是有限时间随机有界的。 XET=EX≥0 (22) (23) (24) (25) 令X-1=P,根据Schur补引理可知条件(22)—(24)成立可得广义模糊系统(5)关于参数[c1,c2,[0,Tf],X]是有限时间随机有界的。 为了验证本文所提方法的有效性,设分数布朗运动的Hurst指数取H=0.78,考虑一个具有2条模糊规则i∈T={1,2}的三维广义T-S模糊系统,系统参数如下: 从而满足定理1的条件,说明该数值系统是有限时间随机有界的。 本文针对带有分数布朗运动的广义模糊系统的有限时间随机有界性问题展开了研究。首先设计了状态反馈控制器,然后针对分数布朗运动导数的特性建立了与Hurst指数相关且带有二重积分的新型Lyapunov泛函,得到了广义模糊系统有限时间随机有界的充分条件,最后通过Matlab进行数值仿真,证明了本文所提方法的有效性。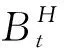

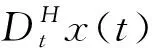

2 T-S模糊反馈控制器的设计




3 广义有限时间有界性分析







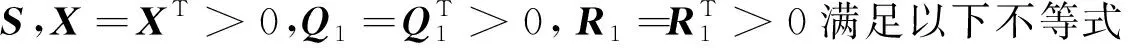
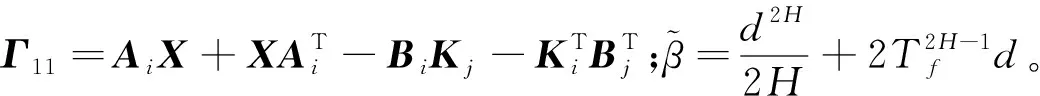

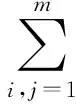


4 数值算例

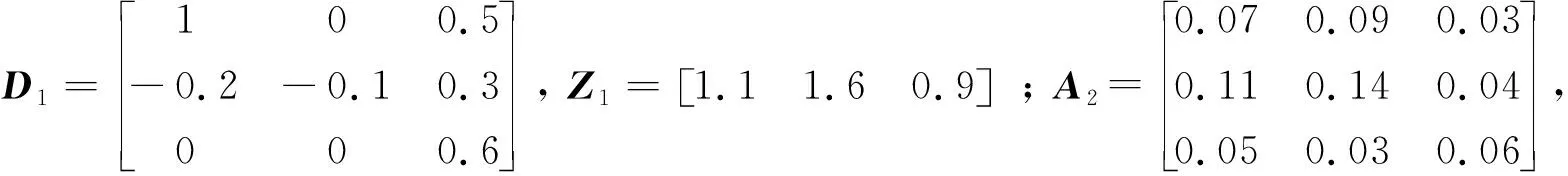

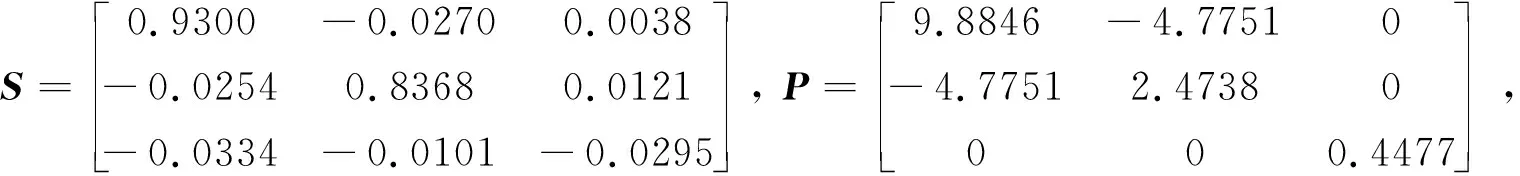
5 结论
