离散型随机变量及其分布列高考二轮复习之决策问题教学案例设计
2021-11-09罗佼佼
罗佼佼
(南宁市第三中学 广西南宁 530000)
一、教学目标
1.学生能够读懂题意,能够提取有用信息和对数据进行处理。
2.理解简单离散型随机变量期望的概念,会计算简单离散型随机变量的期望。
3.面对多种可能发生的情况时,能有分类讨论意识并能找到分类依据进行准确分类。
二、教学重点
1.学生能在大量文字当中提取有用信息,读懂题意。
2.理解简单离散型随机变量期望的概念,会计算简单离散型随机变量的期望。
三、教学难点
对信息量大的题目能做到准确理解题意,有分类讨论意识,并有明确的分类讨论标准
四、解读学生
学生数学基础薄弱,对于概率、分布列知识还仅停留在套用公式计算概率上,对信息量大的题目无法做到准确理解题意,提取有用的信息,缺乏分类讨论意识。
五、近5年的高考分析
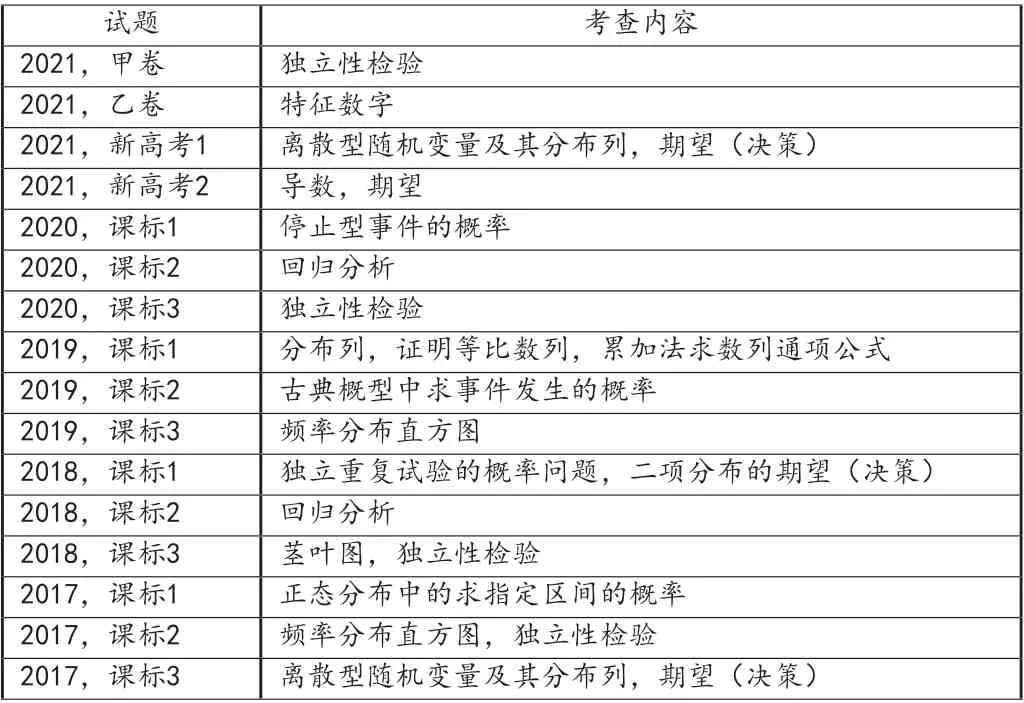
试题 考查内容2021,甲卷 独立性检验2021,乙卷 特征数字2021,新高考1 离散型随机变量及其分布列,期望(决策)2021,新高考2 导数,期望2020,课标1 停止型事件的概率2020,课标2 回归分析2020,课标3 独立性检验2019,课标1 分布列,证明等比数列,累加法求数列通项公式2019,课标2 古典概型中求事件发生的概率2019,课标3 频率分布直方图2018,课标1 独立重复试验的概率问题,二项分布的期望(决策)2018,课标2 回归分析2018,课标3 茎叶图,独立性检验2017,课标1 正态分布中的求指定区间的概率2017,课标2 频率分布直方图,独立性检验2017,课标3 离散型随机变量及其分布列,期望(决策)
从上表可知,近5年高考卷,总共16套卷子,有8套大题考到了概率,其中6套涉及了离散型随机变量及其分布列知识,自2017年开始,概率大题常考利用离散型随机变量及其分布列和期望选择决策,且分布列不再是可以直接套入公式即得结果的二项分布和超几何分布,整个大题更具灵活性和实践性。
六、教学过程
例1:(2017,新课标3改编)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完。根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关。如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶。为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:

最高气温 [10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数 2 16 36 25 7 4
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),超市一天的进货有两种方案:方案一,进货300瓶;方案二,进货400瓶,从利润的角度出发,问哪种方案更好?
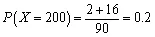
因此X的分布列为

X 200 300 500 P 0.2 0.4 0.4
(2)方案一:若最高气温不低于20,则Y1=(6-4)×300=600;
若最高气温低于20,则Y1=6×200+2(300-200)-4×300=200;

Y1 200 600 P 0.2 0.8
EY1=200×0.2+600×0.8=520
方案二:若最高气温不低于25,则Y2=(6-4)×400=800;
若最高气温位于区间,则Y2=6×300+2(400-300)-4×400=400;
若最高气温低于20,则Y2=6×200+2(400-200)-4×400=0;

Y2 0 400 800 P 0.2 0.4 0.4
因此EY2=800×0.4+400×0.4=480.可知EY1>EY2,所以选择方案一。
设计意图:本例题是由高考题改编而成,高考原题难点在于第(2)问中对进货量n的销售情况进行分类讨论,从而得到不同的进货量n对应的利润Y的分布列,从而得到Y的期望,进而求出期望的最大值。学生往往对于抽象的n分类讨论的标准不清楚,而分类讨论又是高考重点考查的知识与技能,因此,本例题通过具体的进货情况,让学生体验从具体到一般,由浅入深。
变式:把例1中的问题(2)改为“设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?”
解析:由题意知,这种酸奶一天的需求量至多为500,至少为200,因此只需考虑200≤n≤500
当300≤n≤500时,
若最高气温不低于25,则Y=6n-4n=2n;
若最高气温位于区间[20,25),则Y=6×300+2(n-300)-4n=1200-2n;
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n;
因此EY=2n×0.4+(1200-2n)×0.4+(800-2n)×0.2=640-0.4n。
当200≤n<300时,
若最高气温不低于20,则Y=6n-4n=2n;
若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n;
因此EY=2n×(0.4+0.4)+(800-2n)×0.2=160+1.2n。
所以n=300时,Y的数学期望达到最大值,最大值为520元。
设计意图:该变式即为2017年新课标3卷的真题,由例题让学生体会到分类讨论的标准之后,再把确定的进货量变为变量n,把例题考查的知识和能力进行提升。
练习1:(2016,新课标1)某公司计划购买2台机器,该种机器使用三年后即被淘汰。机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元。在机器使用期间,如果备件不足再购买,则每个500元。现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记表示2台机器三年内共需更换的易损零件数,表示购买2台机器的同时购买的易损零件数。
(1)求X的分布列;
(2)若要求P(X≤n)≥0.5,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
解析:(1)由柱状图并以频率代替概率可得,一台机器在三年内需更换的易损零件数为8,9,10,11的概率分别为0.2,0.4,0.2,0.2。
P(X=16)=0.2×0.2=0.04;
P(X=17)=2×0.2×0.4=0.16;
P(X=18)=2×0.2×0.2+0.4×0.4=0.24;
P(X=19)=2×0.2×0.2+2×0.4×0.2=0.24;
P(X=20)=2×0.2×0.4+0.2×0.2=0.2;
P(X=21)=2×0.2×0.2=0.08;
P(X=22)=0.2×0.2=0.04
所以X的分布列为

X 16 17 18 19 20 21 22 P 0.04 0.16 0.24 0.24 0.2 0.08 0.04
(2)由(1)知P(X≤18)=0.44,P(X≤19)=0.68,故n的最小值为19。
(3)记Y表示2台机器在购买易损零件上所需的费用(单位:元)。
当n=19时,E(Y)=19×200×0.68+(19×200+500)×0.2+(19×200+2×500)×0.08+(19×200+3×500)×0.04=4040.
当n=20时,E(Y)=20×200×0.88+(20×200+500)×0.08+(20×200+2×500)×0.04=4080.
可知当n=19时所需费用的期望值小于n=20时所需费用的期望值,故应选n=19。
练习2:(2018长郡中学高三选拔考试)某地4个蔬菜大棚顶部,阳光照在一棵棵茁壮生长的蔬菜上,这些采用水培、无土栽培方式种植的各类蔬菜,成为该地区居民争相购买的对象,过去50周的资料显示,该地周光照量X(小时)都在30以上,其中不足50的周数大约5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周,因蔬菜大棚对光照要求较大,某光照控制仪商家为应对恶劣天气对光照的影响,为该基地提供了部分光照控制仪,该商家希望安装的光照控制仪尽可能运行,但每周光照控制仪最多可运行台数受周光照量X限制,并有如下关系:

?
若某台光照控制仪运行,则该台光照仪周利润为4000元;若某台光照仪未运行,则该台光照仪周亏损500元,欲使商家周总利润的均值达到最大,应安装光照控制仪多少台?
解析:记商家总利润为Y元,由已知条件可知至少需安装1台,
(1)若安装1台光照控制仪可获得周利润4000元;
(2)若安装2台光照控制仪:
当X>70时,一台光照控制仪运行,此时Y=4000-500=3500元,
当30<X≤70时,两台光照控制仪都运行,此时Y=4000+4000=8000元,
故Y的分布列为

Y 3500 8000 P 0.2 0.8
所以EY=3500×0.2+8000×0.8=7100元,
(3)若安装3台光照控制仪:
当X>70时,一台光照控制仪运行,此时Y=4000-1000=3000元,
当50≤X≤70时,两台光照控制仪运行,此时Y=4000+4000-500=7500元,
当30<X<50时,三台光照控制仪都运行,此时Y=4000+4000+4000=12000元,
故Y的分布列为

Y 3000 7500 12000 P 0.2 0.7 0.1
所以EY=3000×0.2+7500×0.7+12000×0.1=7050元,
综上,为使商家周总利润的均值达到最大应该安装2台光照控制仪。
设计意图:进一步加强学生的信息提取能力和数据处理能力,加深分类讨论意识,巩固基础。
七、教学反思
高考二轮复习备考中,我们主要以专题形式对高考中的重点、热点进行复习,帮助学生查漏补缺,建立完整的高考应试的知识方法体系,在离散型随机变量及其分布列大题的第(2)问中,近几年常考写出离散型随机变量及其分布列,以其期望为依据来进行决策,学生往往对这一类文字多、信息量大的题目束手无策。
学生出错的根源有以下两点:
第一,审题不清,无法正确理解题意,无法找到题目中多个变量之间的联系;
第二,分类标准不清楚,无法进行完整的分类讨论。
现在高考都是以核心素养命题,纵观近几年的高考题,概率统计大题文字多、信息量大,需要学生在有限的时间内提取出和问题相关的条件,旨在考查对信息的提取处理能力,因此读懂题目、提取有用的条件在解答题中尤为重要。
那么,如何快速提取有用的条件呢?
首先,可以从问题出发,在题目中找寻与问题相同的关键词,画出或简略罗列条件;其次,抓住题目中变量的个数,找出题目中所有和变量有关的条件,对条件进行梳理,理清变量之间的联系;最后,确定随机变量可能的取值,写出分布列。
分类讨论是高考必考的一类思想方法,学生往往对分类的标准模糊或者分类情况有重复或者遗漏。分类讨论的产生源于我们对情况的不确定,因此分类的标准就是对于不确定的事情进行讨论。例如,对于例题而言,进货量为300或者400时,销售情况是不确定的,销售情况因与气温有关,有可能酸奶全部售完,也有可能酸奶滞销,因此,我们就酸奶销售情况为分类的标准来进行讨论即可。
在今后碰到分布列与决策问题时,我们可以让学生围绕这4条来考虑问题:
1.题目叙述了一件什么事情?做这件事情的规则是怎样的?
2.耐心审题,可适当画出条件或者简单罗列条件,弄清随机变量是什么。
3.决策问题中,通常以期望(反映了随机变量平均取值)为衡量标准,进行方案选择。
4.找出题目中变量的个数和变量之间的联系。
5.遇到不确定的情况,则就可能出现的情况进行分类讨论。
