提炼基本图形 培养几何直观

郭海英

（杭州学军中学教育集团文渊中学，浙江 杭州 310000）

对“几何直观”的理解

对它的认识：“直观”就是当人们接触事物时，借助于观察、经验、想象等所产生的对事物及其关系直接的感知与认识。而几何直观则是借助于见到的或想到的几何图形的形象关系产生的对事物的性质或数量关系的直接感知与认识，几何直观是一种运用图形认识事物的能力。标准指出：“几何直观”是指利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直接地理解数学，在整个数学学习过程中发挥重要作用，

它的意义：20 世纪最伟大数学家希尔伯特在名著《几何直观》一书中谈到：

第一层意思，图形可以帮助刻画和描述问题。一旦用图形把一个问题描述清楚，就有可能使这个问题变得直观、简单。

第二层意思，图形可以帮助发现、寻找解决问题的思路。

第三层意思，图形可以帮助表述一些结果，可以帮助记忆一些结果。

如何帮助学生建立几何直观

第一 要充分的发挥图形带来的好处。

第二 要让学生养成一个画图的好习惯。

第三 重视变换，让图形动起来，把握图形与图形之间的关系。

第四 要在学生的头脑中留住些图形(比如基本图形）。

无论是在“图形与几何”领域的学习还是在其他领域的学习中，都应重视几何直观的培养。

在中考中有许多试题是根据基本图形来巧妙设置的，这样既考查学生提炼图形和运用图形的能力，更是对“几何直观”的一种培养。基本图形具有广阔的拓展空间，根植于基本图形的试题屡见不鲜。挖掘基本图形，有助于更好的培养发散性思维，提高学生分析问题解决问题的能力。今天我们通过展示一些案例跟大家谈谈在第二轮复习中提炼基本图形的方法。

（一）K 字型图

案例1.如图，AB ⊥BD 于点B，CD ⊥BD 于点D，P 是BD上一点，AP ⊥PC,且AP=PC. 你能得到什么结论？

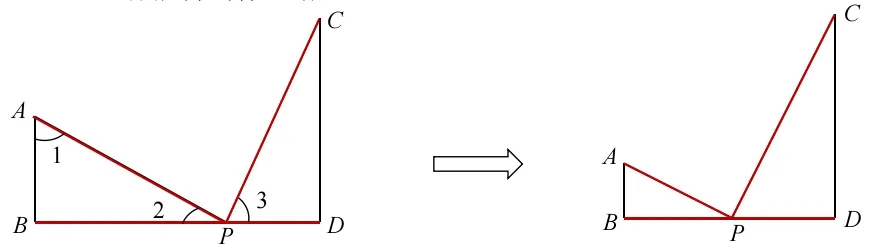
这时我们每个同学都能得出结论：有两个全等三角形，有对应边相等，这个基本图形，我们给它一个名称叫K 字型。如果把条件AP=PC 去掉，那么就能得出两个三角形相似。接下来用K 字型图可以比较快的解决下面的几个习题。

变式1.如图，已知AB ⊥BD,CD ⊥BD,AP ⊥PC,且P为BD 中点，AB=2，BD=6，那么CD=_______直线l2过点B(0,2)且与x轴平行，直线l1与直线l2相交于点P。点E为直线l2上一点，反比例函数

案例2：在平面直角坐标系XOY中，直线l1过点A(1,0)且与y轴平行，的图像过点E 与直线l1相交于点F。

1.若点E 与点P 重合，求k的值；

2.连接OE、OF、EF。若k＞2，且△OEF 的面积为△PEF 的面积的2 倍，求E 点的坐标；

3.是否存在点E及y轴上的点M，使得以点M、E、F为顶点的三角形与△PEF 全等？若存在，求E 点坐标；若不存在，请说明理由。

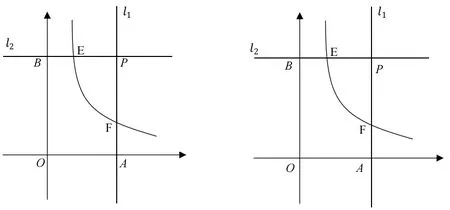
变式1：如图，直线L1 过点A(1,0)且与y轴平行，直线L2过点B(0,2)且与x轴平行，直线L1与直线L2相交于点P.点E为直线L2上一点，反比例函数的图像过点E 与直线L1相交于点F，存在点E及y轴上的点M，使得以M、E、F为顶点，且以EF为直角边的三角形与△PEF 相似，则点E 的坐标____▲___.

（二）K 字图的变形

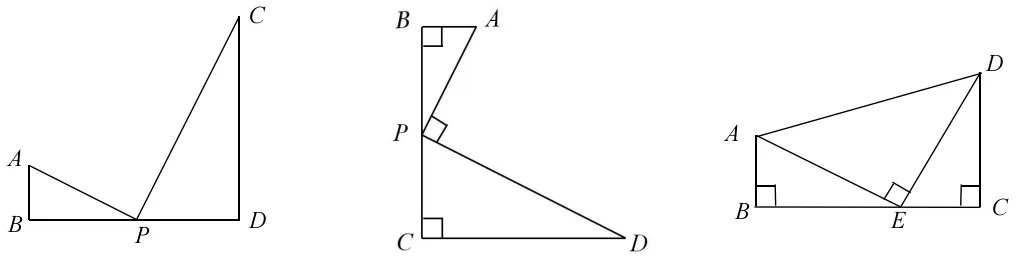
案例2.若直线QE ∥y 轴，将含45°角的直角三角板如图所示放置，你能够得出什么结论？

现在老师已经添了两条辅助性，这对解决本题就不会显得有多大难度了，可以证明两个三角形全等，但是其实这也是前面K 字型图的变形，也可以用K 字型图来解答。现在我们来回顾一道2011年绍兴的中考题24 题，这是一道很典型的以基本图形中K 字变形图作为解题的突破口，就可以轻松拿下了。

对中考第二轮复习教学来说，我们尤其要重视基本图形的提炼和挖掘，如果把一道综合题比喻成一座房子的话，那么具体的知识点就好比砖头、钢筋、水泥等，而基本题、基本图形就好比一堵墙、一个房间。墙与墙之间、房子与房子之间如何搭建，就是解题的思路了。在考场上，面对每一道题目，都要求学生在较短的时间内对解题思路作出选择和判断，如果熟悉一些基本图形，无疑能提高他们探索解题思路的速度。当基本图形直接看不出时，就能想到去构造基本图形。如果把这个K 字型图的直角加以变形，我们可以把这三个角变为相等，顶点不同，但都在一条线上，构成两个三角形（或三个）其中两边上的两个是相似，这就是我们接下来要来运用的“一线三等角”这一基本图形。其实也是一个K字型的变形。

（三）一线三等角

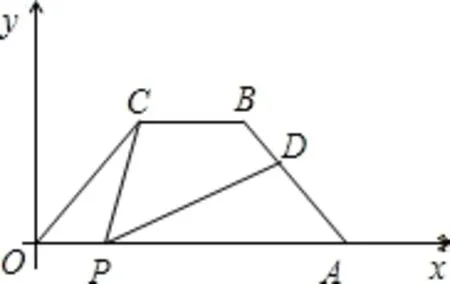
案例1 如图所示，在平面直角坐标系中，四边形OABC 是等腰梯形，BC ∥OA，OA=7，AB=4，∠COA=60°，点P为x 轴上一个动点，（点P 不与O、A 重合），连接CP，过点P 作PD 交AB 于点D.

1.求点B 的坐标；

2.当点P运动到什么位置时，△OCP为等腰三角形，求此时点P的坐标；

这一问题的解答是：填上常用辅助性过点B 作BE 垂直OA,根据已知条件就可以把点B 的坐标得出，第2 小题要用到分类思想，不过在读题目是要注意条件“x 轴上”，所以考虑的范围要扩大到x 轴的负半轴，第3小题如果能发现在同一条线段上又不同顶点的三个角相等，就显得很容易了，用“一线三等角”这个基本图形，存在相似三角形，所以就可以通过OP×PA=OC×AD，从而求得结果。

案例2 .如图.直角梯形OABC 的直角顶点O 是坐标原点，边OA，OC分别在x 轴、y 轴的正半轴上.OA ∥BC，D 在BC上，，AB=3,∠OAB=45°，D 是BC上一点，CD=.E、F 分别是线段OA、AB上的两动点，且始终保持∠DEF=45°，设OE=x，AF=y.

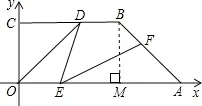
1.证明△ODE ∽△AEF，并确定y 与x 之间的函数关系；

2.当△AEF 是等腰三角形时，将△AEF 沿EF 折叠，得到△A′EF，

求△A′EF 与五边形OEFBC 重叠部分的面积.

解决本题也是跟上面一样的思路，不过现在请同学们自己可以做了吧，证明相似，用的是一线三等角这个基本图形，关键是第2 小题，更能体现这个基本图形的优势，因为△AEF 是等腰三角形，其中的点E、F 都是动点，但是如果能想到只要满足△ODE 是等腰了，那么△AEF 自然也一定是等腰三角形，这就容易多了，因为△ODE 中只有一个点E 是动点，研究起来就比较方便，现在我们就只要分三类情况来讨论解决，画出每一种状态图，请同学们试试吧。相信自己肯定行！

总而言之，利用基本图形及其结论，能够将复杂的问题简单化，帮助学生在较短的时间内抓住问题的本质，并可以防止解题中无关信息的干扰，提高我们的思维水平。