圆锥曲线离心率的求解策略——基于“理解数学”的一点思考与实践

上海市海滨中学 郭卫华

启东市汇龙中学 顾向忠

理解数学，就是要把握数学内容的本质，特别是对内容所蕴含的数学思想和方法要深入理解，要对一些具有统摄性的“一般观念”能自觉应用。“理解数学”有助于整体把握数学结构，准确制定教学目标。离心率一方面体现了函数表达式中参数a，b，c之间的联系，另一方面刻画了椭圆、双曲线的形状，是圆锥曲线的一个非常重要的几何性质。离心率的相关问题往往是高考的热点，该类问题是数学知识的交汇点、数学思想和方法的综合点，其往往有两种题型，即显示约束条件和隐藏约束条件；有两种解题方向，即以“形”为主的解题方向，注意结合平面几何知识求解，以及以“数”为主的解题方向，注意方程和不等式的联系。求离心率的方法通常有以下几种：

一、直接求出a 与c

二、利用几何性质

如果题目中存在“焦点三角形”，那么可以通过焦点三角形包含的边角关系，利用余弦定理或者正弦定理进行求解。如果题目中涉及圆锥曲线的统一定义，那么可以直接通过这个几何性质去求离心率。

三、构造a、c 的齐次式

四、利用图形坐标

有些题目中的几何关系不明确，这时可以将图形中的点坐标用基本量a，b，c来表示，再结合向量的坐标运算列出等式求解。

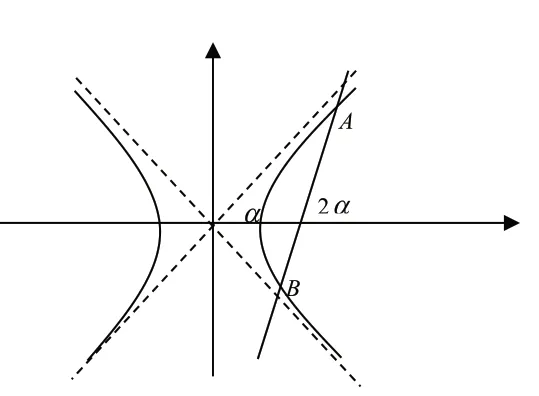
图1

五、利用三角形的相似关系

离心率本身是一个比值，而三角形的相似可得到比例关系，因此可借助于平行构建相似关系。

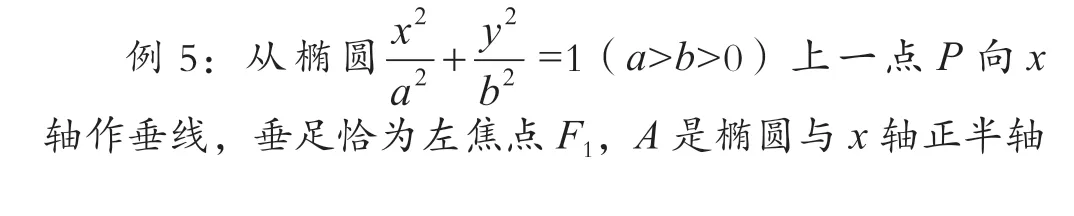
六、利用点线距离关系

圆锥曲线往往和圆综合，圆心到直线的距离常常是考查的对象，而直线一般是渐近线、准线等一些特征量，可以通过点线距离构建等量关系。

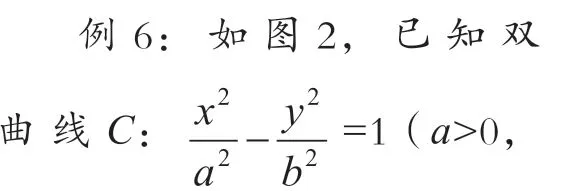
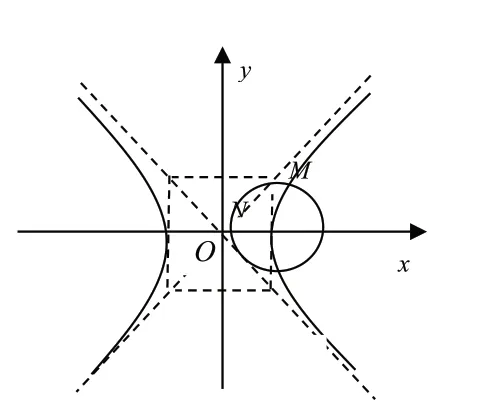
图2

综上，如何求椭圆和双曲线的离心率，重点是围绕方程和已知条件寻找参数a，b，c的等量关系，有时需要结合数形结合的思想求解。

“理解数学”是倡导数学模型教学的核心过程。纵观整个解题过程，是一种学生主动参与、认知结构的自我完善过程，处处体现数学核心素养的融入，注重数学思想方法的归纳与总结，也是一种促进教师业务素质不断提高的教学实践过程，有意识地引导学生从“变”的现象中发现“不变”的本质，同时注重学生对知识的自主生成，最大限度地张扬理解数学的重要性，让学生在探究活动中领悟数学文化的魅力，发展推理能力、运算能力以及自我监控管理能力。这些良好习惯的形成，不仅对培养学生的探索精神和创新意识具有重要作用，而且对培养学生的核心素养也有极大的价值。