绕流中平直与曲壁面周围局部压力的对比研究

李红群

(贵州大学明德学院，贵州 贵阳 550025)

0 引言

绕流现象广泛存在于船舶海洋、水利机械等工程中，不同形状的水下结构在一定速度的来流作用下，其周围会产生分布情况不同的局部压力，对设备的性能及寿命造成一定的影响。钝体绕流是其最基本的绕流形式，当均匀来流以一定的速度流过一物体后，会在该物体周围产生很多复杂的现象[1]。钝体绕流由于其复杂特性以及广泛的工程应用，成为研究人员一直研究的对象。

至今，关于钝体绕流问题，国内外学者们采用不同方法，从不同角度对其进行了分析研究。邢鹏飞等人[2]研究了开缝宽度和角度对圆柱周围压力分布的影响。Tritton[3]通过改进的实验验证了雷诺数约为90时圆柱产生尾涡，以及涡上下脱落的特点和差异。随着计算机的发展，尤其是新方法格子Boltzmann方法(LBM)的提出，引起了钝体绕流的研究热潮。王璐等人采用侵入边界的LBM算法，提高了低雷诺数下圆柱定常流动仿真计算的精度[4]。饶勇等人[5]采用格子Boltzmann方法分析讨论了不同间距下并列双方柱的绕流形态，以及方柱各边上压力与间距比的关系。Perumal[6]等人用格子Boltzmann方法计算了稳定和非稳定流下的方柱绕流，讨论了雷诺数、阻塞比和模型长度对绕流的影响，并验证了该方法能有效地捕捉绕流特征。关于钝体绕流中立柱后方涡脱落现象、升阻力系数影响等方面已经做了很多相关的研究，但是对于不同类型的立柱周围局部点位置的压力分布情况研究相对较少。因此，本文采用格子Boltzmann方法，以程序化的方式建立了LBM数值模型和流场几何模型，对圆柱和方柱分别进行了计算。首先，从升、阻力系数和Strouhal数三个方面验证了模型的正确性；然后，分析了一定雷诺数下(Re=150)立柱周围压力变化规律；最后，讨论了不同雷诺数对立柱周围压力的影响情况。结果发现，方柱和圆柱周围最大压力点是相同的，且位于迎流面的中心处；迎流面各点处的压力变化较大，而背流面各点处的压力值几乎相同。本文所得结果为水下结构物的优化设计和水动力分析问题上提供了一定的参考依据。

1 数值模型

1.1 理论模型

与宏观有限体积法、有限差分法和有限单元法不同的是，基于分子动理论的格子Boltzmann方法将流场划分成离散的网格，将流场内的流体看成一个个介于微观粒子尺度和宏观特征尺度之间的介观流体质点。流体质点按照一定的规则在流场网格节点上进行碰撞和迁移，其碰撞过程[7]表示为：

(1)

迁移过程[7]表示为：

fα(x+eαδt,t+δt)=fα′(x,t+δt)

(2)

(3)

式中，ωα为权重系数，cs格子声速，ρ为流体密度。

1.2 边界处理

LBM的边界处理格式有很多种，根据不同的边界形式合理地选择边界处理格式可以有效地减少边界对流场的影响。为了得到更好的数值结果，本文中计算时针对不同的壁面条件，采用了不同的边界处理方法，平直壁面采用具有虚拟边界的Half-way反弹模型，而曲壁面则采用LBM与有限差分法相结合的形式进行处理，计入了物理边界相对于网格线的偏移量对结果的影响[9]。升力系数和阻力系数是通过流场升力和阻力计算得到，它们均是无量纲参数，计算公式为：

(4)

式中，FD是立柱所受到的阻力，FL是立柱所受到的升力，D为特征长度，umax为来流速度。另一个重要的无量纲参数是Strouhal数(Str)，它反映了涡脱落的快慢，定义为[10]：

(5)

式中，f为涡脱落频率。

2 数值计算结果

2.1 模型验证

文献[11]结果表明了计算区域长度为50D、阻塞比为8、立柱中心与入流边界为12.5D时，区域边界对绕流结果的影响很小。因此，本文的计算区域为50D×8D的矩形，如图1所示。在计算区域尺寸不变的情况下，将图1中的圆柱换为方柱即得到方柱绕流的计算区域。其中圆柱直径(方柱边长)D为立柱的特征尺寸，D取20。

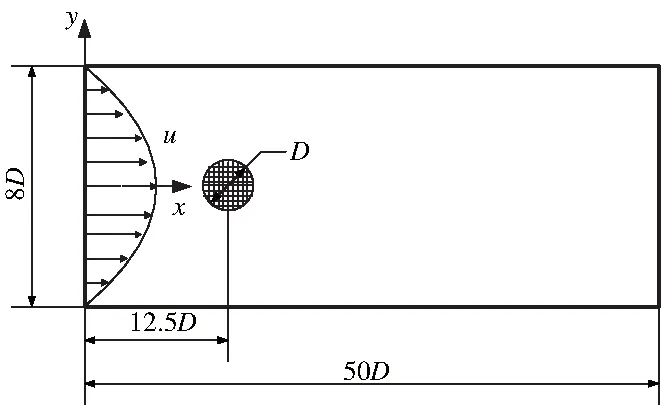
图1 钝体绕流几何计算域

为了真实地模拟出水流经过障碍物，入口边界设为均匀来流，轴向速度为抛物线分布，即：

(6)

式中，H为计算域宽度，这里取8D；y表示该方向粒子瞬时移动的长度，取值范围为[-H/2，H/2]；ux为轴向(x方向)上的速度；umax为轴线上粒子最大的速度，y向速度为0；出口边界的速度梯度为0，其余边界为无滑移边界。

雷诺数定义为：Re=umax·D/v，v为粘度。在雷诺数为150时，计算得出方柱和圆柱的无量纲参数如表1所示。从表1可得：在同一雷诺数下，本文所得结果与已有文献结果几乎一致，验证了本文模型的正确性。

表1 Re=150时圆柱绕流的无量纲参数

2.2 不同角度上平直与曲壁面周围的压力

由于结构模型的上下对称性，先对立柱上半部分进行研究，并通过监测立柱边界上关键点的压力来讨论立柱周围压力的变化情况。平直与曲壁面周围的压力分布云图如图2所示。

图2 绕流压力图中柱体周围各关键点

在方柱左边界、上边界和右边界分别取3个点，圆柱边界上取9个点，位置分别是0度、30度、45度、90度、120度、135度、150度和180度。得到了绕流过程中立柱周围各关键点位置处的压力随时间变化曲线，如图3所示。

从图3(a)1中看出，方柱迎流面的压力从边界中心向上(或向下)递减，在点4位置得到最小的压力，随着1点到4点的最大压力向最小压力的变化，压力曲线上下波动越明显。同时从曲线递减的程度来看，与点1、点2相比，点3处的压力与点4处的压力值相差很大，说明该边界上的压力相差不大，但能很快过渡到最小压力。从图3(a)2中知道，方柱上边缘的压力值，除了最小压力值外，其余各点的压力几乎相同，且该边缘的压力曲线上下变化的幅度大小几乎相等。从图3(a)3可以看到方柱背流面各处压力值的大小几乎相等，但曲线变化幅度不一样，点9处幅值最小，说明了压力幅值随着背流面中心向两端增大。这三幅图的曲线说明了方柱周围各面的压力变化规律是不一致的。

从图3(b)1可以得出，圆柱迎流面上180度位置上的压力比背流面0度和上边缘90度位置处的压力都大，0度和90度位置上的压力值相差很小，这说明了，钝体绕流对迎流面的影响较大，而对其他面来说影响就较小。图3(b)2的变化和图3(a)3的变化趋势较一致，背流面处各点的压力值相差不大。图3(b)3为迎流面各点处的压力变化，与图3(a)1不同的是，圆柱周围各点处压力变化较均匀。

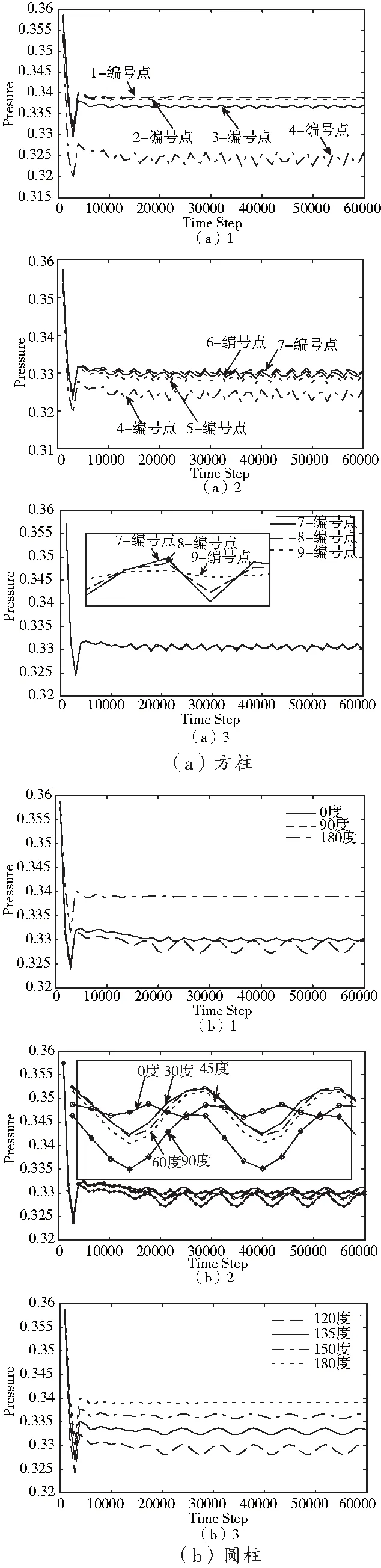
图3 立柱周围各关键点位置处的压力

2.3 雷诺数对压力的影响

前面讨论了一定雷诺数(Re=150)下，钝体绕流中立柱周围压力的变化。为了探究不同雷诺数对立柱周围压力的影响，本文研究了雷诺数为20、50、150、200、 400这5个工况下立柱周围压力的变化情况，得出了立柱最大压力随时间的变化曲线，如图4所示。

图4 不同雷诺数下立柱周围的最大压力值

从图4可以看出，随着雷诺数的增大，图4(a)和图4(b)的变化趋势均是先减小后增大，压力值的波动幅度都增大，这符合绕流的特性，即流态发生变化，由层流逐渐过渡到了紊流状态。在所研究的几种工况中，发现图4(a)中雷诺数为150时的压力最小，而图4(b)中雷诺数为150和200时压力几乎达到最小。图4(a)中雷诺数为150、200、400的三条曲线之间的间隔较大而图4(b)中对应的曲线重合较多，说明在雷诺数为150、200、400下的绕流对方柱周围压力的影响比圆柱的大。

3 结论

本文通过方柱和圆柱的绕流计算，验证了模型的正确性，分析了雷诺数为150时立柱周围的压力变化，讨论了不同雷诺数对立柱周围压力值的影响。结果发现，在其他条件都相同的情况下，方柱周围和圆柱周围压力变化既有相同点又有不同点。相同点：一是绕流中，方柱和圆柱迎流面各点处的压力变化较大，最大压力位于迎流面中心，背流面上各点处的压力几乎没什么变化，其他面各点的压力变化很小；二是，迎流面处，随着最大值向最小值变化过程中，压力波动的幅度均逐渐增大；三是，最大压力都是随着雷诺数的增加呈现先减少后增加的趋势。不同点：主要体现在不同雷诺数下立柱周围压力值变化的过渡值不一样，在所研究的5个工况中，方柱在雷诺数为150时获得的压力最小，而圆柱在雷诺数大约为150～200时获得的压力最小。该结果对工程设计及水动力特性的分析起到了一定的参考作用。