向量键合图在平面多体系统建模中的应用研究*

单东升，梁 全，牛 彪

(沈阳工业大学机械工程学院，辽宁 沈阳 110870)

0 概述

复杂系统建模和仿真，通常可能涉及到多领域交叉的建模和仿真工作。随着科技的发展，机械领域的分析与控制变得愈发重要。传统的机械系统分析方法大多数只是单独一种能量形式的系统，不能适用于多领域交叉的耦合系统。

键合图是多能域统一建模的一种有效工具，它能统一各种能域，只用一种理论就可以建立完整的机电液混合系统的模型，是实现多领域交叉的复杂耦合系统进行动态分析建模和仿真的有效方法[1]。传统键合图理论已经发展成熟，在液压系统、电气系统、机械系统以及风力发电等领域的建模仿真中都有着不错的表现[2-5]，然而在对多体系统进行建模时还存在很多问题。

多体系统由数量有限的刚体组成，通过任意关节相互连接。由于多体机械系统存在多刚体相互作用，因此刚体间存在运动几何约束，使得键合图模型内部存在很多非线性的结型结构。进行运算时需要反复迭代方程，出现微分因果环，所以此时传统键合图法还不适合在计算机上进行全局动力学分析。许多学者为此提出了一些解决办法，这些方法在对复杂机械系统的描述过程中，通过标量键合图建立的模型会非常繁琐、复杂，从而对分析求解模型的过程造成阻碍，容易出错。多维度的键合图可以弥补标量键合图的不足，并成为了近些年键合图理论的研究热点，例如针对于双曲柄六杆压力机构动力学仿真问题的向量键合图法[6]、围绕Delta型3D打印机多能域耦合动力学建模的旋量键合图法[7]等。

诸多研究热点中，向量键合图具有结构简洁、形式紧凑的优点，但是长期以来国内外对于向量键合图的研究大多数局限于多体系统的图形表示，应用于模型仿真时需要分解成标量形式，从而再次导致了复杂的图形模型，失去了其紧凑图形的优势。同时关于向量键合图与计算机自动建模仿真相结合的实现，研究空间还很大。本文针对这些不足，对基于向量键合图的多领域复杂系统建模和仿真进行了研究。

本文提出了三种针对平面多体系统进行建模的向量键合图基础模型：自由刚体的向量键合图模型，两种速度转换的向量键合图模型。基于容性元的特性方程得到了各种运动关节的向量键合图模型的搭建方法。由此，分别搭建了单摆模型，双缸并联平台模型，并在20-sim软件中对模型进行仿真，仿真结果证明建模的合理性。

1 基于向量键合图的基础模型介绍

基于三维的向量键合图理论，分别建立自由刚体模型及两种速度转换模型，共三种基础模型。通过容性元特性方程限制运动关节的自由度，得到各种运动关节的向量键合图模型。对以上模型进行封装，模块化。

1.1 自由刚体模型

自由刚体的表示基于牛顿-欧拉方程，经过变矢量的绝对导数与相对导数定理的转换，可以得到：

(1)

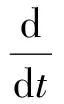
对应式(1)建立自由刚体的向量键合图模型如图1所示。

图1 自由刚体向量键合图模型

较高的共流结代表惯性系中的质心速度向量v，前者连接表示刚体惯性的惯性元；较低的共流结代表质心角速度向量，前者连接表示刚体主轴转动惯量的惯性元；自制的MGR元件与GR元件的值为：

MGR：ω×(m·v)

(2)

GR：ω×(J·ω)

(3)

1.2 速度矢量转换模型

速度矢量的转换分为两种，一种是刚体内部任一点处速度矢量的转换，另一种是不同坐标系间的速度矢量转换。

基于基点法可求得刚体内任一点的速度，因此，势变量对应的方程为：

M=F×r

Mi=εijkFjrk

(4)

流变量对应的方程为：

v=ω×r

vi=εijkωjrk

(5)

式(4)与式(5)符合变换器形式，因此刚体内的任意两点A和B的速度矢量转换的向量键合图模型如图2所示。

图2 刚体内部两点速度矢量转换

不同坐标系间的速度矢量转换是指速度矢量在刚体的体固坐标系与运动关节的中间坐标系(各轴与惯性系平行)之间的相互转换。本文采用欧拉角法实现了这种转换，如式(6)所示。欧拉角α、β和γ定义了三种连续有序的旋转：γ是绕z轴旋转的角度，β是绕y轴旋转的角度，α是绕x轴旋转的角度。对体固坐标系中的速度矢量依次左乘α、β、γ三个欧拉角旋转矩阵便可得到中间坐标系中的速度矢量，三个欧拉角旋转矩阵相乘可以写成相应的正交变换矩阵，如式(7)所示。

ωG=Tω

vG=Tv

(6)

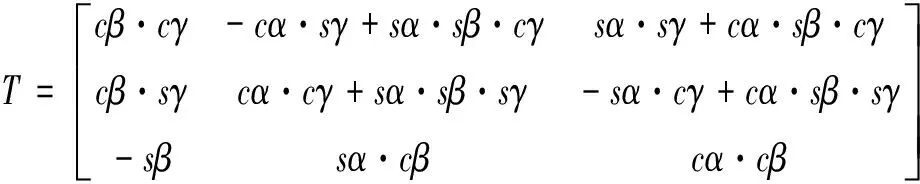
(7)

式中：ωG、vG—中间坐标系的角速度与线速度；ω、v—体固坐标系中的角速度与线速度；c=cos,s=sin。

因此速度矢量从体固坐标系转换到中间坐标系的向量键合图模型如图3所示。

图3 坐标系转换模型

图3中的RotTrans模块内置正交变换矩阵，输入信号是经过体固坐标系中角速度调制的欧拉角。

1.3 运动关节的实现

运动关节是刚体间的连接部分，它需要限制了空间中的一些自由度，本文是基于设置容性元来实现的，容性元的特性方程为：

(8)

其中：e(t)—势变量；q(t)—流变量；C0—线性容度参数。

容性元内置参数设置非常小时，容性元所连接的键上势变量与流变量的值都近似为0，在容性元上键接一个共势结(与共势结连接的键上势相同，流之和为0)，因此当共势结与容性元连接的键上流近似为0时，与共势结连接的另两条键上的流数值是近似相等的。通过这样设置容性元，使得关节具有一定的柔性而不是完全刚性，取越小的容性元参数，运动关节的刚度越大；反之，取越大的容性元参数，运动关节的柔性越大。

以绕x轴转动的转动关节为例，转动关节只有一个方向上转动的自由度不受限制，其向量键合图模型如图4所示。

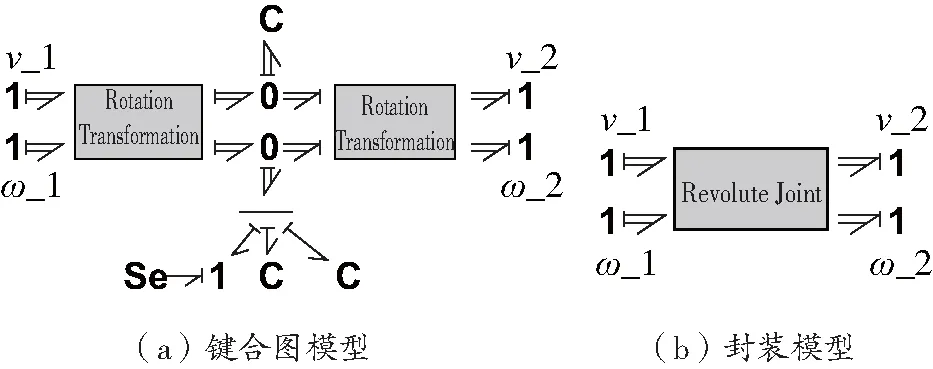
图4 转动关节的向量键合图模型

1.4 模型验证

假设某单摆长为0.1 m，左端点A点固定在坐标原点上，右端点为B点，单摆在YOZ平面内与OY轴成-30°；单摆质量为0.065 kg，转动惯量为4.4×10-5kg·m2，不计阻尼，在YOZ平面在重力作用下做单摆运动，该单摆模型在Amesim软件中如图5(a)所示，其未完全模块化的向量键合图模型如图5(b)所示。

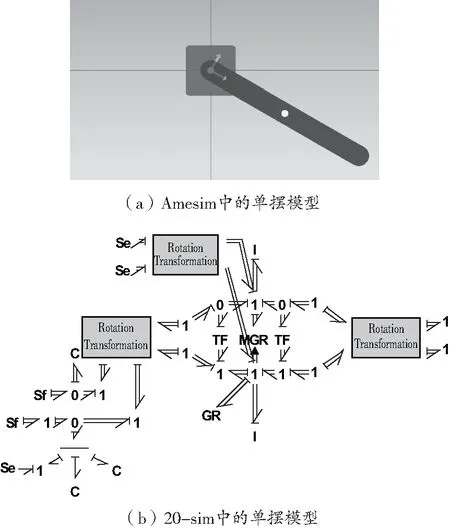
图5 单摆模型

两个势源通过坐标系转换施加到单摆刚体的质心上，以此模仿重力；单摆左端通过旋转关节与两个流源Sf=0连接，起到将单摆左端点与地面固连的作用。

需要对3个坐标系转换子模型的内置正交变换矩阵右乘一个矩阵：

[1,0,0;0,sqrt(3)/2,0.5;0,-0.5，sqrt(3)/2]

以此对应单摆与OY轴成-30°，在20-sim软件中输出仿真曲线如图6所示。

图6 单摆模型位移输出曲线

两个模型的曲线输出结果一致，验证了曲柄滑块的向量键合图模型的正确性。

2 双缸并联平台多能域耦合建模与仿真

2.1 双缸并联平台的向量键合图模型

某双缸并联平台的简图如图7所示，左驱动杆不可以转动，横梁长为L，左右驱动杆未伸缩时的自由长度为r，由两个阀控缸控制平台的姿态，平台系统的自由度是2。

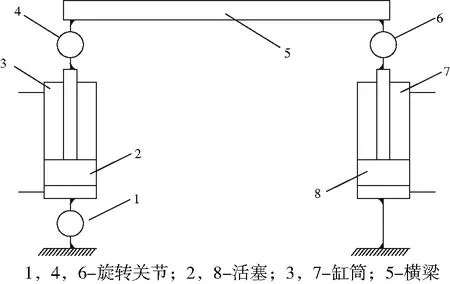
图7 双缸系统示意图

阀控缸通过传统键合图进行建模，在此不进行详述[8]，阀控缸的模型与平台的多体模型通过一个伸缩关节连接，如图8所示。

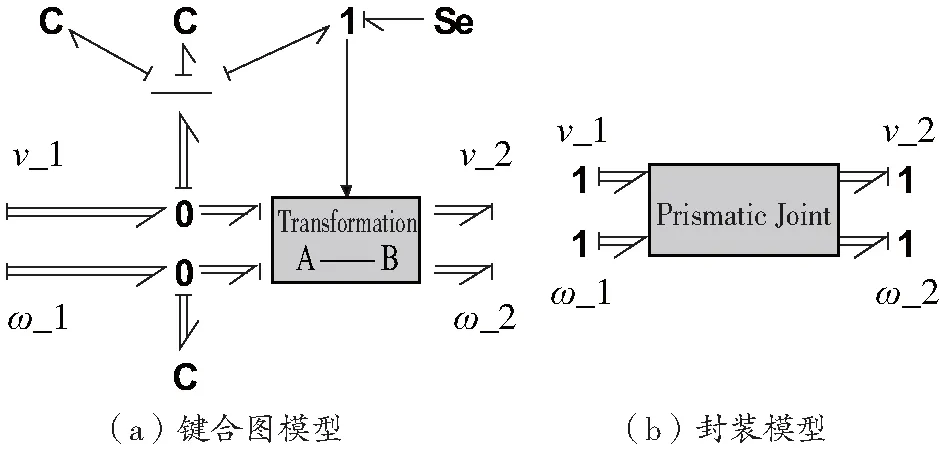
图8 伸缩关节的向量键合图模型

通过容性元限制了3个转动和2个平动的自由度，允许两个连接刚体在z轴方向上的两个极限点之间存在相对移动，图7中的刚体内部转换子模型通过液压缸的极限位置端点进行了调制；势源在这里代表液压缸的作用。

输入期望姿态信号通过自编运动学反解模块输出信号到阀控缸，阀控缸采用闭环PID控制；双缸多体系统按照结构功能进行一次封装，其一级子模型如图9(a)所示其子模型命名对应于图7中编号；通过系统功能进行二次封装，其主模型如图9(b)所示，通过逐级封装，模块化的双缸并联平台的模型变得非常简洁。

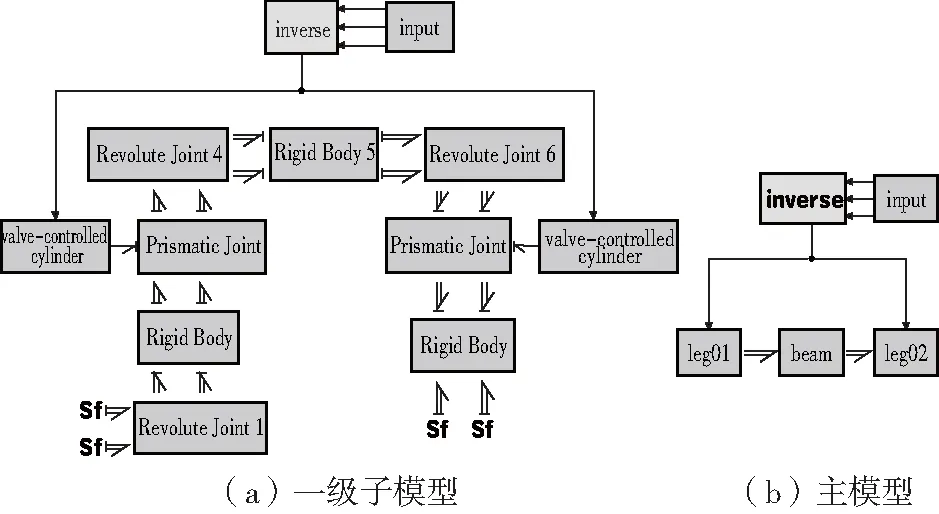
图9 20-sim中的双缸并联平台

2.2 算例

给定双缸并联平台多体结构部分的尺寸参数：横梁长及左右驱动杆未伸缩时的自由长度分别为L=5 m，r=3 m，初始位置时两个驱动杆与横梁垂直，横梁负载为5000 kg。输入期待值alpha=0.2 rad，y=0.05 m，z=0.5 m。

此时平台质心位姿及双缸状态的输出如图10所示。

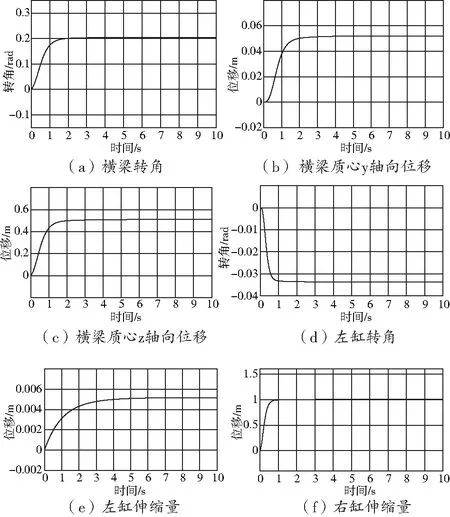
图10 仿真输出曲线

平台质心的输出曲线稳态值与输入的期待位姿信号一致，运动学反解算法与平台模型互相验证正确，运动学反解模块输出信号与双缸伸缩量一致，说明平台的多体结构建模正确，对平台的控制成功。

3 结论

基于向量键合图理论，提出了3种针对多体动力学系统进行建模的基础模型。文中以单摆模型为例，验证了3种基础模型以及通过容性元限制运动关节自由度的正确性；以双缸并联平台为研究对象，实现了多体系统与阀控缸系统相结合的多领域统一建模与仿真。

研究结果表明：

1)提出的向量键合图基础模型对多体系统的表达意义清晰，输出正确，可用来表达任何平面多体结构；通过对基础模型与各种运动关节进行封装，实现模块化建模，形式更简洁。

2)以本文基础模型搭建的双缸并联平台多体结构的向量键合图模型与阀控缸的传统键合图模型结合，实现对双缸并联平台系统的建模与仿真验证。基于本文所述基础模型，可以与其他传统的标量键合图模型连接，用统一的方式处理多能域耦合的平面多体系统的动力学分析问题。