“质心”在高中物理中的应用
2021-11-08江苏冯得会
江苏 冯得会
质心是一个特殊的位置,质心与质心系是讨论质点系运动的重要概念。本文首先对质心的概念与相关的规律进行了介绍,然后结合质心在高中物理教学以及解题中的应用实例,对质心概念和规律的应用做了举例分析,为学生处理多物体所组成的系统问题时,提供了另外一种分析的角度。
一、质心的概念及规律
如果将一支粉笔抛出,让它在空中旋转,粉笔上每一个点的运动情况都非常复杂,但是事实上存在着这样一个特殊的点,好像粉笔的所有质量都集中在这一点,作用在粉笔上的重力也集中在这一点,使它的运动沿着简单的抛物线路径,就好像抛到空中的质点一样。这个特殊的点就叫质量中心,简称质心。
1.质心的位置
2.质心的速度和动量
3.质心的加速度和质心运动定理
二、“质心”在高中物理教学中的应用实例
1.双星以圆轨道绕质心转动
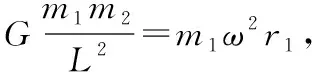
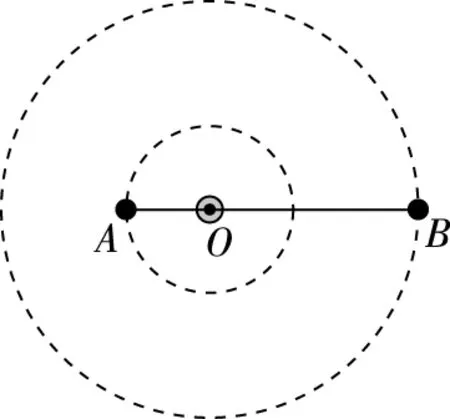
图1
2.弹性碰撞速度公式的另类推导


图2
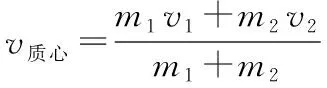
碰撞前,小球1相对质心的速度v相1=v1-v质心
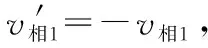

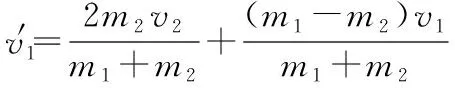
与教材上结论一致,同时更方便记忆;
同理可得碰后小球2的速度:
三、“质心”在高中物理解题中的应用
高中阶段当我们处理的对象为多个物体所组成的系统时,运用系统质心概念及规律,可以为我们提供另外一种分析的角度。下面通过3道例题,试作分析。
1.如图3所示,在光滑的水平地面上放有一质量为M的半圆柱体,在其圆心正上方静止放有一质量为m的光滑小球。某时刻小球受到轻微扰动,由静止开始下滑。当m与M分离时,m的水平位移为xm,则M的位移为
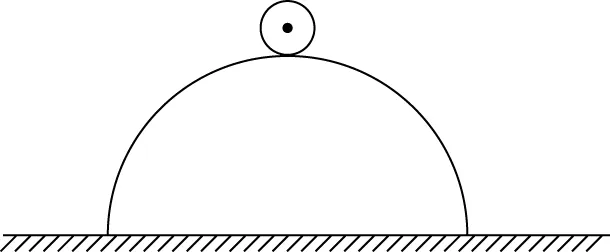
图3
( )
【解析】方法一:系统水平方向不受外力作用,水平方向系统动量守恒。
则mvmx+M(-vMx)=0,
即mxm+M(-xM)=0,
又因为xm+xM=L,
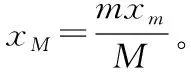


图4
2.如图5所示,在水平圆盘上,沿半径方向放置物体A和B,mA=4 kg,mB=1 kg,它们分居在圆心两侧,与圆心距离为rA=0.1 m,rB=0.2 m,中间用细线相连,A、B与盘间的动摩擦因数均为μ=0.2,设最大静摩擦力等于滑动摩擦力,g=10 m/s2。若圆盘从静止开始绕中心转轴非常缓慢地加速转动,求A、B两物体相对圆盘将要滑动时,圆盘转动的角速度ωm。
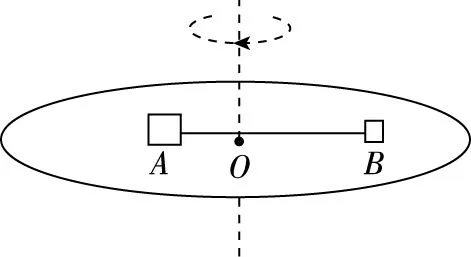
图5
【解析】方法一:规定由A指向O方向为正方向,
对A、B系统,由系统牛顿第二定律可得:
F合=mAaA-mBaB=(mArA-mBrB)·ω2
当A、B相对圆盘将要滑动时,
F合max=μmAg+μmBg
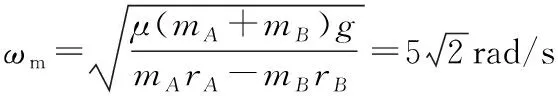
方法二:以O点为坐标原点,建立坐标系,AB系统的质心位置:
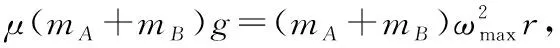
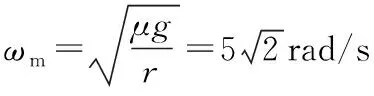
【点评】本题如果对A、B使用隔离法,分析其所受静摩擦力的大小和方向随转盘角速度缓慢变大过程中的变化情况,可以得到A所受的静摩擦力方向指向圆心,逐渐变大,直到达到最大静摩擦力。而B开始所受静摩擦指向圆心,先变大后变小,减小为零后,改变静摩擦力方向,再次变大,达到最大摩擦力,过程比较复杂。方法一和方法二即是直接抓住最终临界状态的特点运用系统规律进行求解。
3.如图6所示,长为2L的轻杆上端及其正中央固定两个质量均为m的小球,杆的下端有光滑铰链与水平面相连接,杆原来竖直静止,现让其自由倒下,则A着地时的速度为多少?

图6
【解析】方法一:对系统利用机械能守恒定律:
又vA=2vB

方法二:由两小球质量相等,可知其质心位于两小球连线中点位置。假设着地时质心角速度为ω,由机械能守恒:
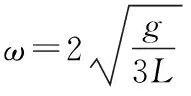
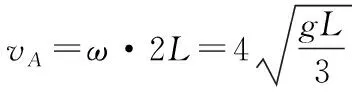

四、小结

