交通荷载作用下矩形隧道结构动力响应研究
2021-11-08黄光强马少坤
黄光强,马少坤
(1.中铁四院集团南宁勘察设计院有限公司, 广西 南宁 530003;2.广西大学 土木建筑工程学院, 广西 南宁 530004)
0 引言
为缓解交通压力,提高道路通行能力,我国城市交通建设近年来得到迅速发展,城市路网逐渐趋于空间化、立体化和规模化,越来越多的隧道工程将下穿已有城市道路[1]。然而,城市地面道路交通荷载复杂,在车流量大、拥堵的交叉口路段,交通荷载对下方浅埋隧道结构产生的动力响应不可忽视。特别是当隧道本身存在损伤时,车辆动荷载所引起的隧道结构响应更加显著,危及隧道结构的服役寿命。因此,研究不同荷载工况组合作用下隧道结构的动力响应对隧道结构设计和安全性能评估具有重要意义。
众多学者对交通荷载引起的隧道动力响应问题展开了相关研究。例如,赵俊澄等[2]分析了在不中断交通条件、不同支护方案下超浅埋隧道的动力响应特征,以此来评估在复杂交通作用下下穿浅埋隧道的施工安全性;郭春霞等[3]通过三维动力有限元模型,分析了车辆荷载和地铁列车荷载对隧道结构的动力响应;黄晓吉[4]针对富水地区中的隧道系统,基于饱和土体的Biot理论,考虑隧道衬砌与外围土体的相互作用,分析了交通荷载作用下衬砌隧道系统的动力响应;王建炜等[5]以上海某公铁两用隧道为例建立了隧道-土体系统的三维动力有限元模型,对公路和轨道交通载荷单独作用及共同作用时的隧道动力响应进行分析,获得了公铁两用隧道的动力响应规律;田甜等[6]通过现场试验和有限元数值模型计算的方式,对衬砌在速度300 km/h列车荷载作用下的加速度响应规律进行了研究;魏纲等[7]利用MIDAS GTS NX软件建立沉管隧道三维有限元模型,通过对路床网格节点添加线性变化的荷载来模拟车辆行驶,对车辆荷载下沉管隧道的动力响应进行了分析;杨文波等[8]采用模型试验与数值模拟相结合的方法,采用频率响应函数和峰值振动加速度作为评价指标,对高速列车振动荷载作用下马蹄形断面隧道动力响应特性进行了分析。
上述研究均表明了交通荷载对隧道结构的动力响应及变形影响不可忽视。但不同工况下,隧道结构的受力变形特征不同,对于复杂交通条件下的隧道动力响应研究仍没有较具体的工程经验可以参考。同时,本研究实例具有交通荷载复杂、隧道超浅埋、上覆公路交通流量大等特点,且所研究的隧道为大断面矩形隧道,目前相关研究涉及较少。因此,将根据实际交通荷载情况,开展不同工况组合作用下矩形隧道的动力响应规律的研究,为评价矩形隧道在交通荷载作用下的安全性及结构设计提供理论参考。
1 工程背景
扬子江路准快速化改造一期工程(杨柳青路-司徒庙路,全长约1 880 m,其中地面道路长635 m、地下道路长1 245 m(含隧道长971 m)。为缓解扬子江路高峰期拥堵情况,对道路进行主辅分离式断面改造,即在交叉路口建设下穿隧道。主线隧道位于下层连续下穿台扬路、平山堂路,上层辅道与平山堂路平交,隧道位置见图1。本工程拟采用装配式建设方案,隧道主体结构拟采用装配式预制拼装法施工。
本文以台扬路-平山堂路交叉口为例,研究复杂交通荷载对隧道结构的动力响应影响。台扬路-平山堂路段隧道埋深约2.7 m,为矩形双跨隧道,隧道断面宽26.2 m,高7.4 m,断面图如图1所示。设置双向四车道,设计速度60 km/h。扬子江道路通行能力约为2 800 pcu/h,交叉口高峰时段饱和度达到0.9。

图1 扬子江隧道与地面位置关系
2 数值模拟
2.1 模型构建及参数选取
根据扬子江下穿平山堂路段的实际情况,采用ABAQUS软件建立三维动力响应分析模型,整体三维模型如图2所示。计算模型沿隧道纵向长度取50 m,横向宽度取150 m,地面到模型底部取40 m。数值模拟主要顺序为:初始地应力平衡、隧道结构建设以及车辆荷载工况分析,其中施加荷载分析步采用动力隐式分析步[9]。土体和隧道结构均采用C3D8R八节点减缩积分实体单元进行模拟。土体采用摩尔—库伦弹塑性本构模型[10],由于本研究只针对隧道的瞬态响应,不考虑其塑性形变,所以隧道结构采用弹性本构模型。为了避免振动荷载产生的振动波传到固定边界会发生反射,导致动力计算结果不准确,模型底部及四周采用粘弹性人工边界,模型上部设为自由边界[11]。土体与隧道结构之间设置法向“硬”接触,切向“罚”接触,摩擦系数取0.7,允许滑移变形[12]。在模拟时对模型进行了简化。假设土体为均质连续性土体且具有各项同性,隧道埋深取最小覆土厚度2.7 m。

图2 整体三维模型
根据地质勘察资料及室内试验资料,确定本文数值模拟所用地层以及隧道结构材料参数见表1。

表1 材料参数
2.2 模拟交通荷载
交通荷载是一种动荷载,具有低频性、瞬态性、循环性、随机性等特点。因为车辆的速度远慢于路面的波速,车辆行驶引起的动力响应并不明显,所以如果路面足够平稳,移动车辆对地面动态响应的影响可以忽略,然而,路面不可能完全平整,且路面平整度随着使用时间的延长而变差[13-14]。车辆在不平整路面上行驶产生振动,从而产生超出静荷载部分的附加动荷载即为引起动力响应的关键。根据前人研究所得,可用一种能反映车辆移动速度和路面平整度的简谐波动荷载模型来近似表达交通荷载,本文采用随时间变化的简化正弦荷载来进行动力分析[15],荷载模型表达式为
(1)
式中,F(t)为车辆荷载, kN;P0为车轮静载,kN;P为车辆荷载振动幅值,kN;ω为振动圆频率,ω=2πv/L(ν为车辆的运行速度;L为几何曲线的波长,取车长)。
根据《公路沥青路面设计规范》(JTGD 50—2017)[16]中的BZZ—100标准,取车轮静载P0为100 kN;车辆荷载振动幅值P与车速和路面不平整度有关,根据文献[17],当行车速度为60 km/h时,振动幅值P取0.3P0,车辆荷载激振时程曲线如图3所示。进行数值模拟时,为了方便动荷载的施加,将车辆荷载折算为一组间距1.5 m,宽0.5 m,长1 m的均布简谐波动荷载,隧道内车辆荷载位置如图4所示。实际工程中机动车道旁为人行道,此处不考虑人群荷载。

图3 车辆荷载激振时程曲线

图4 车辆荷载位置示意图
结合工程的实际情况,本文对3种典型荷载工况进行模拟,荷载工况见表2。

表2 荷载工况
2.3 动力监测点
由于扬子江隧道下穿城市道路,十字交叉口处交通荷载情况复杂,因此交叉口下方的隧道断面振动情况成为评估该隧道性能的重点。为避免边界效应,选取隧道中段的2 m断面进行分析。由于隧道为对称结构,故取左跨进行研究,分布在隧道底板跨中内侧、隧道顶板跨中外侧、侧墙跨中内侧、中墙跨中这4个位置布置拾振点,如图5所示。以下将分别从加速度、速度、位移这三个方面对隧道结构在不同荷载工况下的动力响应进行分析。

图5 拾振点位置
3 动力计算结果与分析
3.1 加速度响应
在交通荷载组合作用下,各拾振点不同工况下隧道结构的竖向和水平加速度响应时程曲线分别如图6和图7所示。由图6可知,车辆简谐荷载作用下,隧道结构受迫振动,各特征点竖向加速度变化趋势与荷载变化趋势一致,工况2、工况3作用下隧道结构的响应值均大于工况1,工况2作用下隧道结构振幅约为工况一作用下隧道结构振幅的1.5倍,工况三作用下隧道结构振幅约为工况一作用下隧道结构振幅的1.35倍。竖向加速度响应程度由D→B→A→C点呈减弱趋势,说明车辆荷载作用引起的竖向加速度响应主要集中在中墙和顶板,对侧墙影响较小。

(a) 工况1
由图7可知,工况一、工况三中各特征点的水平加速度响应值均大于工况二,其中C点(侧墙位置)最为明显,工况二中的B点(顶板位置)水平加速度响应峰值最大。研究表明:当地面上行车与隧道内行车方向一致时,地面车辆荷载引起的水平加速度响应从顶板向下传递,逐渐衰减;地面行车荷载与隧道行车荷载所引起的水平加速度响应方向相反。D点(中墙位置)几乎不产生水平加速度响应。车辆同时在隧道内和地面上与隧道垂直的方向行驶时,产生的水平加速度响应值最大,侧墙位置达到0.14m/s2。总之,隧道结构受到的动力响应由地面和隧道内的车辆荷载共同决定,研究隧道结构的动力响应时,需对这几种工况进行分析。

(a) 工况1
3.2 速度响应
车辆动荷载作用下,各拾振点的振动趋势大致相同,因研究重点为地面交通荷载,故取顶板特征点B,不同工况下B点的速度响应时程曲线如图8所示。从图8中可明显看出,不同工况下的速度响应时程曲线趋势基本一致,工况2、工况3的竖向速度明显大于工况1,工况2、工况3作用下的波动振幅几乎是工况1的两倍,说明地面车辆荷载作用对隧道结构产生的振动响应明显,而且竖向速度响应程度远大于水平速度。
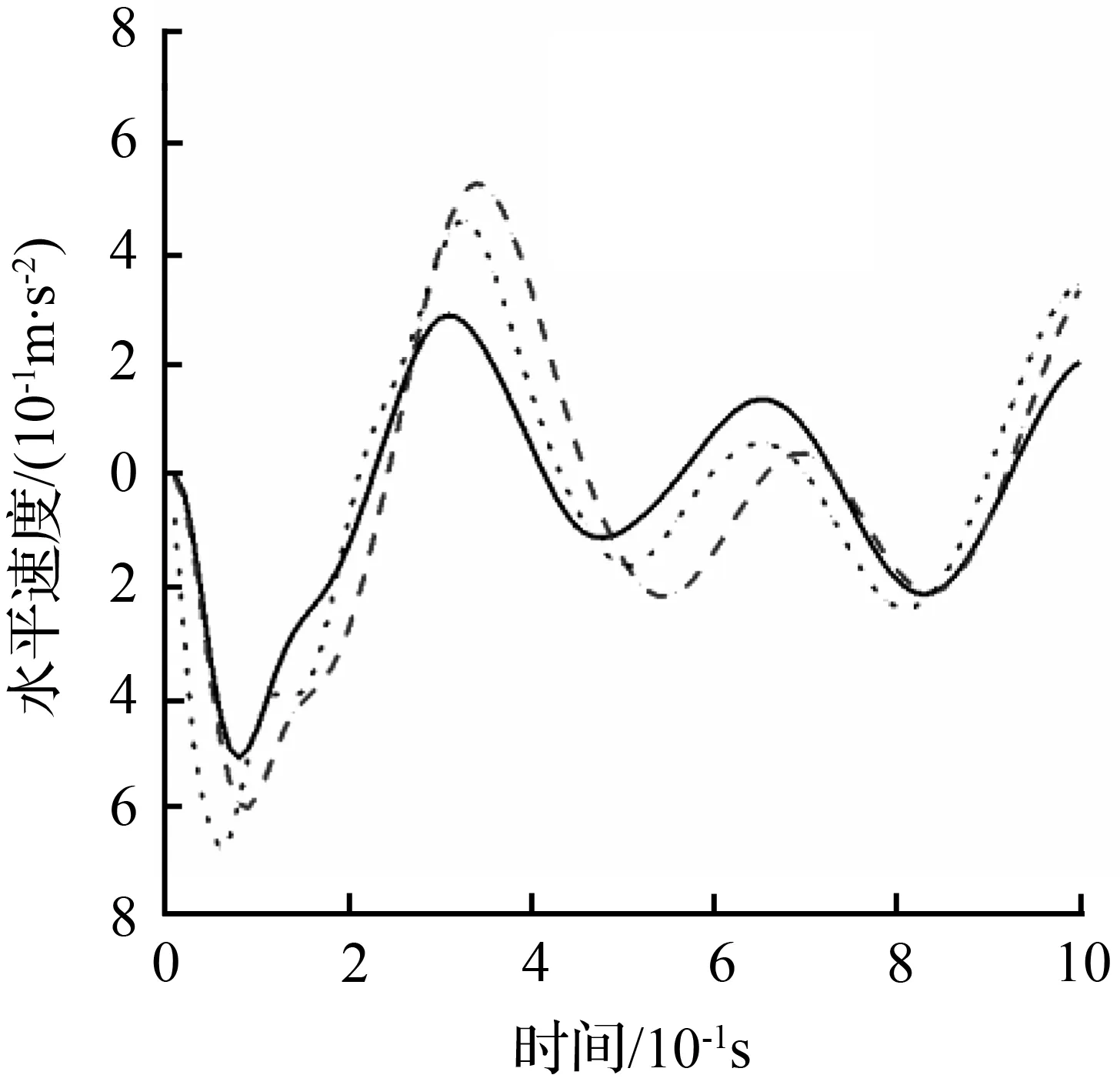
(a) 竖向速度
不同工况下各特征点的速度响应峰值见表3,从表3可看出:工况2、工况3的竖向速度大于工况1,其中顶板的竖向速度峰值最大;各工况中C点(侧墙位置)水平速度峰值最大,D点(中墙位置)水平速度峰值最小,其中工况二中C点的水平速度峰值远小于其他工况,说明当车辆在地面上沿着与隧道平行的方向行驶时,引起的速度响应方向与车辆在隧道内行驶引起的速度响应方向相反,与上文的分析结果吻合。

表3 不同工况下各特征点的速度响应峰值
3.3 位移响应
位移是评估动力响应影响的重要安全性指标。图9为不同工况下隧道结构的动力响应位移峰值。由图9(a)可看出,工况2和工况3的竖向位移峰值都大于工况1,隧道结构各部位竖向位移响应情况差不多,地面车辆荷载引起的竖向位移响应幅值范围为1.00~2.07 mm。由图9(b)可看出,C点(侧墙位置)在3种工况作用下的水平位移峰值最大,说明侧墙位置产生的水平位移响应最强烈,而侧墙往往是装配式隧道接头的位置,因此在进行接头设计时需谨慎考虑衬砌结构的水平抗剪能力;D点(中墙位置)几乎不产生水平位移响应。3种工况作用下侧墙位置的水平位移峰值关系:工况1>工况3>工况2,其中工况1作用下C点的水平位移峰值达到0.20 mm,工况2水平位移最小,说明当地面车辆与隧道内车辆同时行驶时,引起的动力响应从各自的作用位置向四周扩散,方向相反,在这种长年累月的循环荷载作用下,隧道侧墙极易发生水平剪切疲劳损伤。

(a) 竖向位移峰值
在复杂交通荷载作用下,隧道结构的最大瞬态响应位移值达到5.18 mm,而且竖向位移响应值远远大于水平位移响应值,可见地面交通荷载对隧道结构的沉降影响不可忽视。此外,采用装配式隧道方案时,需考虑隧道接缝的竖向抗剪能力。
4 结论
① 交通荷载作用下,隧道结构的加速度、速度、位移时程曲线均呈周期性变化,说明隧道结构实际上受到循环荷载的作用。车辆荷载激振曲线与隧道结构动力响应参数的时程曲线变化趋势近似相同。
② 车辆荷载所引起的隧道动力响应呈现竖向动力响应远大于水平动力响应的特点。
③ 隧道内行车和地面上行车都会对隧道结构产生一定的动力响应,地面上行车引起的位移响应值约占总响应值的24.4%~40.0%,说明地面行车引起的动力响应影响明显。隧道顶板瞬态响应位移峰值达到5.18 mm,受地面行车影响最大。
④ 交通荷载作用下,侧墙位置水平方向上的加速度、速度、位移响应值最大;当地面车辆与隧道内车辆同时行驶时,引起的动力响应从各自的作用位置向四周扩散,传播方向相反,在这种长年累月的循环荷载作用下,隧道侧墙极易发生水平剪切疲劳损伤。
