地铁隧道重叠段的沉降变形特性研究

李辉,文波,张路

(1.陕西铁路工程职业技术学院， 陕西 渭南 714000；2.西安建筑科技大学 土木工程学院, 陕西 西安 710055)

0 引言

近年，地铁工程得以蓬勃发展，但受施工条件限制，近接施工问题愈发明显，尤其是隧道重叠段的地表沉降变形问题尤为突出，进而开展该问题的研究具有重要意义[1-2]。目前，已有相关学者开展了地铁隧道施工过程的地表沉降研究。一方面，部分学者侧重于地铁隧道施工过程中的地表沉降影响因素分析，如吴贤国等[3]利用粗糙集理论的约简处理获得了隧道施工过程中地表沉降的关键因素，为其后续变形预测模型奠定了基础；利用数值模拟分析了施工过程的沉降影响因子，所得结果与现场监测成果具有较好的一致性[4-5]。另一方面，部分学者侧重于地铁隧道施工过程中的沉降预测研究，分别构建了多种沉降变形预测模型，所得结合与实测值较为相符[6-7]。上述研究取得了相应的研究成果，如构建沉降变形预测模型时的影响因素筛选能有效保证预测精度；沉降变形预测对现场事故防治具有重要意义等。但是，上述研究也存在一定的不足，如均是盾构施工条件下的工程实例背景，未涉及暗挖方法的地表沉降规律研究；也未充分结合地铁隧道施工过程中的沉降影响因素筛选及其预测；预测模型相对较为单一，未实现沉降变形的组合预测研究等。

因此，为克服上述问题，笔者以深圳地铁5、7号线的重叠段工程为实例背景，先利用数量化理论Ⅲ筛选隧道重叠段地表沉降的主要影响因素，进而保证后续预测模型输入信息的准确性；其次，再引入多种组合预测思路，实现地表沉降的组合预测，以期保证预测结果的精度及其稳定性。

1 基本原理

1.1 影响因素筛选模型

数量化理论Ⅲ可实现定性变量的定量评价，已被广泛应用于隧道及其他相关岩土领域[8]，具有较好的适用性，进而将其引入到地铁隧道重叠段地表沉降影响因素的筛选过程中。

同时，通过数量化理论Ⅲ的求解，可得到m个特征值及其对应的特征向量，进而得出类目得分向量不具唯一性，但根据数量化理论Ⅲ的基本原理，特征值越大，其对应特征向量的可信度相对越高，为实现综合评价，提出以最大三个特征值对应的特征向量为基础，进行各因素的影响程度筛选。

由于三个特征值对应特征向量的可信度存在一定差异，为实现三者组合，提出通过三个特征值进行归一化处理，得到三个特征向量的组合权值，进而组合得到综合特征向量，并利用综合特征向量开展各项目的影响程度评价。在评价过程中，将评价指标确定为得分范围R和方差比η，两者计算公式为

Rj=maxbjk-minbjk, 1≤k≤rj,1≤j≤m,

(1)

(2)

式中,bjk为第j个项目中第k个类目的得分；σjk2为第j个项目的方差;σyk2为所有因素的总方差。

值得指出的是，得分范围R和方差比η的求解方法不同，代表意义也不一样，为消除两者单位等信息的影响，提出对两者进行归一化处理，将两者的归一化值相加，得到综合评价指标Z，且Z值越大，对应项目的影响程度相对越大；反之，影响程度相对越小。

根据上述原理，虽解决了相关问题，但仍有两个问题待解决，即类目区间的划分原则和项目影响程度的划分标准。目前，上述两者多是根据使用者的经验进行划定，具有一定的主观性，为实现合理分析，提出三区间划分原则进行类目区间划分，即将各类目的分布区间等分为三个区间，以实现类目区间的定量划分；同时，项目影响程度的评价指标为Z值，其取值区间为0～2，将大于1范围内的项目定义为重要项目，0.5～1的项目定义为次要项目，小于0.5的项目定义为一般项目。

1.2 组合预测模型的构建

在以往组合预测模型中，多是采用单一组合方法，且缺少单项预测模型的参数优化研究，为克服上述两问题，将组合预测过程分为两阶段，即单项预测模型优化研究和组合预测研究。

1.2.1 单项预测模型优化处理模型的构建

由于单项预测模型是组合模型的基础，进而有必要开展单项预测模型的优化研究；BP神经网络、ELM模型和SVM模型在地铁隧道工程中具有较好的适用性，因此，将上述三类模型作为组合预测的单项预测模型。鉴于三种模型的基本原理已在相关文献[9-12]中进行了详述，不再赘述。

同时，为保证单项预测模型的预测精度，再对三类模型进行优化研究，优化过程具体如下：

① BP神经网络优化。利用遗传算法优化BP神经网络的初始权值及阈值，进而构建出GA-BP神经网络模型，以期增加BP神经网络的全局寻优能力及训练速度。优化过程为：先对遗传算法进行初始化，并将BP神经网络的初始权值及阈值作为染色体属性；其次，以训练误差为评价指标，通过训练过程的选择、交叉及变异实现全局寻优，并输出优化后的初始权值和阈值。

② ELM模型优化。ELM模型是一种新型智能模型，虽具有较好的预测精度，但预测误差不可避免，进而有必要进行误差弱化处理，以提高预测精度，且利用M估计弱化ELM模型预测结果的误差值，其准则为保证所有误差的累加值最小。

通过对误差累加函数的求导及最小二乘估计交换，可将上述误差值的弱化问题转变为权值矩阵β的求解问题，而权值矩阵的求解则可通过M估计的迭代计算实现。根据上述，M估计的优化过程主要是对预测误差进行弱化处理，并将优化后的预测模型命名为R-ELM优化模型。

③ SVM模型优化。在SVM模型的预测过程中，其模型参数核函数及惩罚因子能较大影响预测精度，为保证其预测效果，提出利用粒子群算法实现上述两参数的优化处理，进而构建出PSO-SVM模型。优化过程为：先对粒子进行初始化设置，并将核函数及惩罚因子作为粒子属性；其次，计算各粒子的适应度值，并与全局极值进行对比分析，同时，改变各粒子的位置和速度，并重复计算其适宜度值，如此重复循环，直至达到迭代次数或期望值。

1.2.2 组合方法的设定

组合预测模型按组合方式大致可分为线性组合和非线性组合两类，前者的组合权值是定值，而后者则是非定值，因此，对两种组合方式的效果均进行探讨研究，且结合文献[11]的研究成果，线性组合方法包括误差权值法和方差权值法，两者均是以三类单项模型预测结果的误差值或方差值为基础指标，通过归一化处理得到线性组合权值；同时，非线性组合方法包括RBF权值法和BP权值法，两者均是以三类单项模型的预测结果为输入信息，再以对应实测值为输出信息，进而构建出的非线性组合模型。

2 实例分析

2.1 工程概况

受施工条件限制，深圳地铁5号线和7号线在施工过程中具有一段重叠，其中，5号线在重叠段的里程为：右线(DK35+931.6～DK36+201)，共计长269.4 m；左线(DK35+994.8～DK36+201)，共计长206.2 m。7号线在重叠段的里程为：右线(SK0+542.4～SK0+823.2)，共计长280.7 m；左线(SK0+605.6～823.2)，共计长217.6 m。同时，在空间结构方面，5号线位于7号线上部，竖直净距0.9～1.4 m，平均净距为1 m。其中，5号线采用双联拱隧道设计，高度为7.1 m，宽度为12.3 m，而7号线隧道为左右独立的马蹄形隧道，高度为6.5 m，宽度为6.5 m。

两隧道均是采用浅埋暗挖法施工，原计划7号线先行，待7号线完工后再施工5号线，但受2011年深圳大运会影响，先对5号线进行了施工，且鉴于两隧道属近距离施工，加之周边近接建筑物复杂，因此，在7号线施工过程中进行了现场地表沉降监测，以掌握重叠段的地表沉降规律。

2.2 数据准备

地铁隧道重叠段施工过程中的沉降影响因素可分为三个方面，即隧道几何条件、水文地质条件和开挖支护条件，具体影响因素的识别如下：

① 隧道几何条件。该因素主要是体现隧道几何尺寸及其空间位置，进而将其二级指标确定为隧道跨度(B1)、隧道高度(B2)和隧道埋深(B3)三类，且三类二级指标可从设计图纸及其支护参数上直接识别。

② 水文地质条件。深圳地区整体围岩条件相对较差，且地下水埋深相对较浅，则水文地质条件对地表沉降具有重要影响，其二级指标共计包含6项，即压缩模量(B4)、摩擦角(B5)、黏聚力(B6)、水平渗透系数(B7)、竖直渗透系数(B8)及孔隙比(B9)。上述各影响因素的识别具有一定困难，为实现上述各参数统计的准确性，提出以纵断面设计图纸及室内试验数据为基础，通过厚度加权综合确定上述参数值。

③ 开挖支护条件。若开挖支护条件较优，将会减弱结构变形而引起的地表沉降变形，反之，则会增加地表沉降，加之，重叠段属浅埋段，因此，开挖支护条件对地表沉降具有较大影响。结合工程实际，可将开挖支护条件的二级指标确定为辅助方式(B10)、支护方式(B11)和开挖速度(B12)，其中，B10指的是超前支护方式，根据设计可分为小导管注浆、中管棚支护和大管棚支护三类；B11主要包含单一复合式衬砌、复合式衬砌+上部锚杆、复合式衬砌+全隧道锚杆。为便于上述B10和B11的统计，将两参数的二级指标分别用1、2、3代替。同时，B12则以现场实际施工速度进行识别统计。

根据上述，可得隧道重叠段沉降影响因素评价体系如图1所示。同时，通过现场监测，得到地铁隧道重叠段沉降监测样本见表1。

结合前述类目划分依据和表1的现场统计结果，将本次隧道重叠段数量化分析的项目、类目划分统计见表2。由表2可知，隧道重叠段数量化分析的项目共计有12个，类目共计36个。

2.3 沉降影响因素筛选

如前所述，通过Matlab软件编程计算得到本次数量化理论Ⅲ分析结果的最大三个特征值分别为0.233 8、0.076 8和0.063 8，对应的组合权值分别为0.624 5、0.205 1和0.170 4。隧道重叠段沉降因素的类目得分见表3。从表3可见，当特征值不同时，对应特征向量存在一定差异，即对应类目得分存在不同，验证了通过组合方式确定综合得分向量的必要性。

同时，以类目综合得分向量为基础，求解各项目的得分范围R和方差比η，并以组合值Z评价各项目的影响程度。隧道重叠段沉降影响因素筛选结果见表4。

由表4可知，不同项目对隧道重叠段沉降变形的影响程度存在差异，验证了本次影响因素筛选的必要性；同时，根据Z值的影响程度划分，得出隧道跨度B1、内摩擦角B5和支护方式B11的影响程度相对较高，属重要项目，所占比例为25%；压缩模量B4、隧道高度B2、竖向渗透系数B8、辅助方式B10和水平渗透系数B7等因素的影响程度相对次之，属次要项目，共计有5个，所占比例为41.67%；其余4个影响因素，属一般项目，对隧道沉降的影响有限。

根据上述，得出3个重要项目和5个次要项目对隧道重叠段沉降变形的影响较大，进而将其作为后续预测模型的输入层。

2.4 变形预测分析

将1～19号样本作为训练样本，20～25号样本作为验证样本，且预测过程主要包含两阶段，分述如下：

2.4.1 单项预测模型优化研究

如前所述，单项预测模型为BP神经网络、ELM模型和SVM模型，且为保证三者模型参数的最优性，分别利用遗传算法、M估计和粒子群算法优化三者参数。通过预测，得到单项预测模型参数优化前后的预测结果见表5。

由表5可知，在各单项预测模型的相应验证节点处，参数优化后预测结果的相对误差值均出现了不同程度的减小，说明通过参数优化能很好地提高预测精度，验证了上述三种优化模型的有效性。

通过单项预测模型的参数优化，有效提高了各单项预测结果的预测精度，验证思路的有效性。

2.4.2 组合预测研究

① 线性组合方法

利用误差权值法和方差权值法实现隧道地表沉降的线性组合预测，其中，误差权值法是以各单项预测结果的相对误差为指标，通过归一化处理，得到各单项预测模型的组合权值；方差权值法与前者相似，只是其指标为各单项预测结果的方差值，进而，该方法是从预测结果稳定性角度出发得到组合权值。同时，通过单项预测结果的统计及计算，得到组合权值分别为：

误差权值法：0.335 0.324 0.342；方差权值法：0.179 0.489 0.332。

通过计算，得到线性组合预测结果见表6。

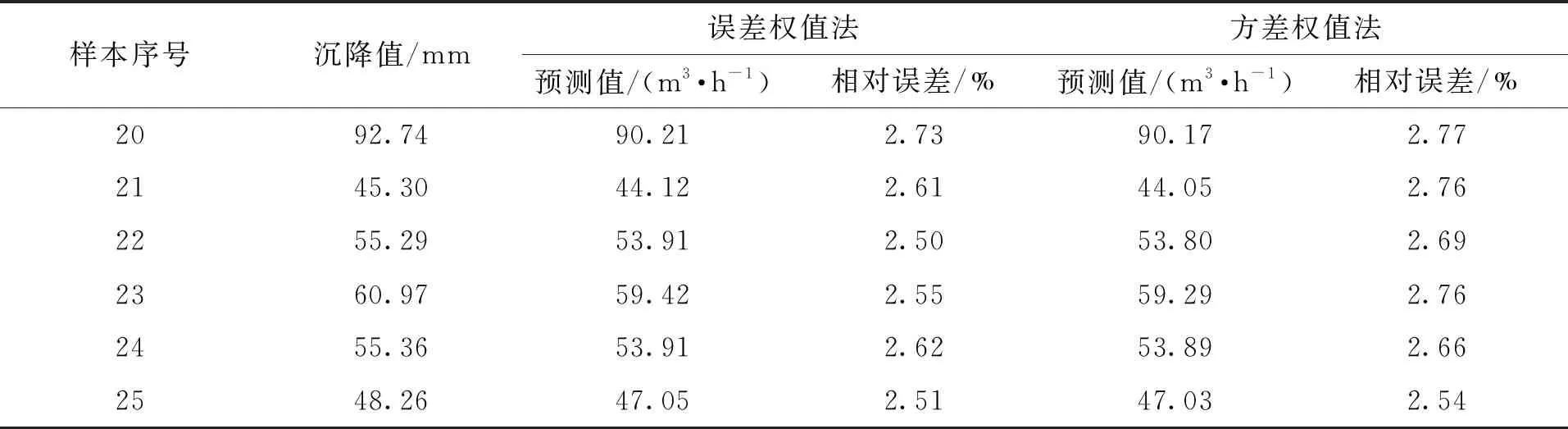
表6 线性组合预测结果

② 非线性组合方法

非线性方法包括RBF权值法和BP权值法，两者均是以三类单项预测结果为输入信息，再以对应实测值为输出信息构建出的非线性组合方法，其组合预测结果见表7。

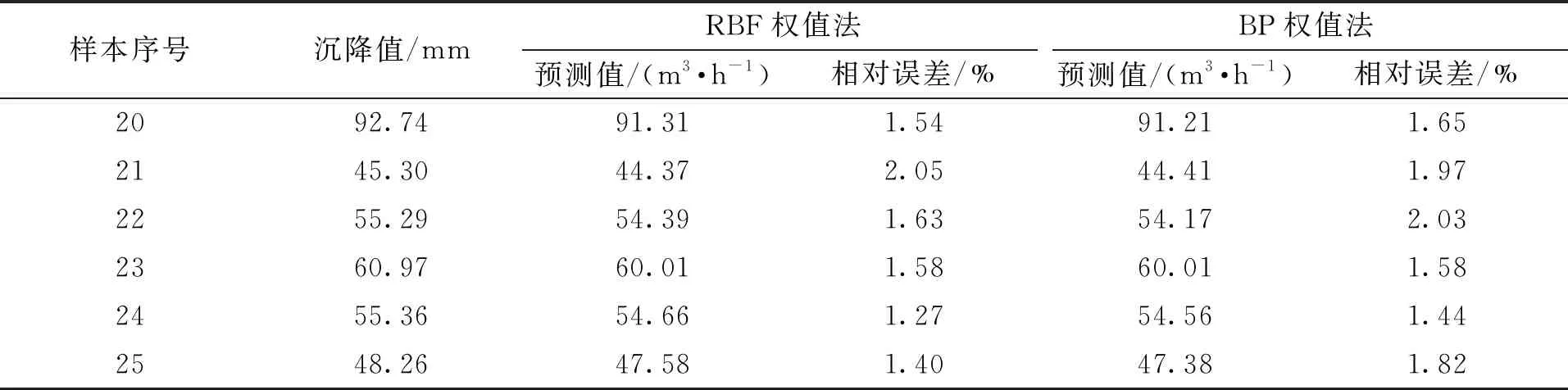
表7 非线性组合预测结果

在RBF权值法的组合结果中，最大相对误差仅为2.05%，相对误差均值为1.58%，而在BP权值法的组合结果中，最大相对误差也仅为2.03%，相对误差均值为1.75%，得出两者均具有相对较高的预测精度，且以RBF权值法的组合效果相对略优。

为对比不同组合方法的预测效果，分别对各模型预测结果的相对误差均值进行统计分析，不同模型的预测精度对比见表8。

表8 不同模型的预测精度对比

首先，对比各单项预测模型优化前后的预测精度，得通过参数优化预测，各单项预测模型的预测精度均得到不同程度的提高，说明单项预测模型的优化研究是很有必要性的；其次，在组合预测模型中，线性组合较单项预测模型的预测精度略优提高，但非线性组合方法的提高效果较高，且以RBF权值法的组合效果相对最优，说明本文组合预测方法均能不同程度的提高预测精度，并以非线性组合方法的效果相对更优。

3 结论

通过数量化理论Ⅲ对地铁隧道重叠段沉降影响因素的筛选及组合预测模型对其沉降变形的预测研究，主要得出如下结论：

① 隧道重叠段的沉降影响因素较多，通过数量化理论Ⅲ可定量评价各因素的影响程度，其中，重要因素有3个，次重要因素有5个，一般因素有4个，将3个重要因素和5个次重要因素作为沉降变形预测的输入层信息。

② 单项预测模型的参数优化可很好地提高预测精度，进而单项预测模型的优化研究很有必要，且各组合预测方法均能不同程度提高预测精度，并以非线性组合方法的效果相对更优。

③ 由于隧道所处地质条件的差异性，使得隧道施工过程中的沉降变形影响因素具有一定的差异，进而在本文模型的推广应用中，有必要结合具体工程实际进行针对性的开展影响因素筛选和预测模型选择，以便保证分析结果的准确性。