尺寸效应对岩石动态力学行为的影响研究
2021-11-08巫绪涛相福斌张瑞乾万航航
巫绪涛, 相福斌, 张瑞乾, 沈 鹏, 万航航
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
0 引 言
由于在细观尺寸上,作为矿物颗粒集合体的岩石材料存在大量的裂隙、孔洞等缺陷,反映在宏观力学性能方面的一个典型特点就是尺寸效应,即采用不同尺寸岩样进行力学试验时,其强度、变形等性能参数显著不同,无法直接用于岩体工程设计及岩石本构理论构建。因此,尺寸效应一直是岩石力学中未解决的热点问题之一。
区别于材料离散性导致的力学性能随机误差,尺寸效应导致岩石力学性能的偏差具有固定的统计分布规律。静态单轴抗压试验的影响因素较少,试验较容易完成,是目前尺寸效应研究和分析的基础。大部分研究发现,岩石的抗压强度随试样尺寸增大而减小,当尺寸加大到一定范围时抗压强度趋于稳定[1-4]。因此,国际岩石力学学会规定抗压强度试验岩样的长径比为2.0~2.5。依据不同的试验数据,研究者提出了众多描述尺寸效应的经验公式,例如岩石强度反比于体积幂次方公式[2]、岩石强度随尺寸增大呈指数型衰减公式[3]、岩石力学参数与长径比之间的统一指数型关系[4]等。关于产生尺寸效应的原因,早期一些研究主要归结为岩石材料的非均质性,即岩石尺寸越大则内部的微缺陷越多;也有一些研究将其归结为试验机压头与岩样间的摩擦效应,其影响程度随岩性变化而变化[4-5]。
近年来,随着爆破工程、抗爆震结构研究的发展,岩石的动态力学行为越来越受到关注[6-10],研究的重点是岩石强度随应变率的变化规律(率敏感性)。由于高应变率加载下惯性效应不能忽略,试验过程中试样必须满足受力均匀性假定,其尺寸不能太大,国际岩石力学学会建议的长径比为0.5~1.0。如果尺寸效应对岩石力学行为影响严重,动态和静态采用不同长径比试样进行试验,那么两者数据无法在一起分析和讨论。目前围绕岩石动态力学行为的尺寸效应已有一些研究报道,例如文献[9]研究了不同类岩石在相同长径比、不同直径条件下的动态力学行为,文献[10]研究了不同长径比岩石动态力学参数的变化规律。但总体来看,岩石动态力学行为尺寸效应研究尚处于起步阶段,试验数据较少,结论差异较大。本文选择2种岩性显著区别的砂岩进行静、动荷载下抗压强度尺寸效应研究,希望结合材质、长径比、应变率多个因素对岩石动力性能的变化规律进行较系统的分析与讨论,并给出分离式霍普金森压杆(split-Hopkinson pressure bar,SHPB)试验条件下岩石材料试样尺寸选择的建议。
1 岩样与试验原理
1.1 岩样
试验选用的岩石种类包括灰砂岩和红砂岩,2种砂岩质地均匀,结构稳定,颗粒直径0.5 mm左右,其中红砂岩富含氧化铁,强度较高。岩样的公称直径ds均为48 mm(国际岩石力学学会建议直径为50 mm,由于所用SHPB装置压杆的直径为50 mm,试样直径须略小于压杆),长径比ls/ds包括0.5、1.0、1.5共3种。根据材质、长径比不同,岩样共分成6个组别。所有岩样均对端面进行磨削加工,控制其不平行度小于0.1 mm。
用电子万能试验机对2种砂岩进行了轴向压缩试验,每组别3~4个岩样静态抗压强度fsc的平均值见表1所列。

表1 2种砂岩不同长径比下的fsc 单位:MPa
1.2 试验原理
冲击压缩试验采用直径50 mm直锥变截面SHPB装置完成,其试验简图如图1所示。高压气体驱动撞击杆以速度v撞击入射杆,产生沿入射杆向右传播的入射波εi(t),与试样作用后,反射波εr(t)沿入射杆向左传播,透射波εt(t)沿透射杆向右传播。εi(t)、εr(t)及εt(t)由入射杆和透射杆上粘贴的应变片、超动态应变仪及瞬态波形存储仪采集。为了减小入射波弥散,在入射杆左端面加φ15 mm×2 mm橡胶垫片作为波形整形器。由于SHPB试验的应变率取决于岩样属性,无法在试验前获得,因此在岩样属性相同的情况下,同一应变率采用相同的撞击杆弹速和波形整形器控制。为了减小压杆与岩样间的摩擦,接触面均匀涂抹凡士林润滑。
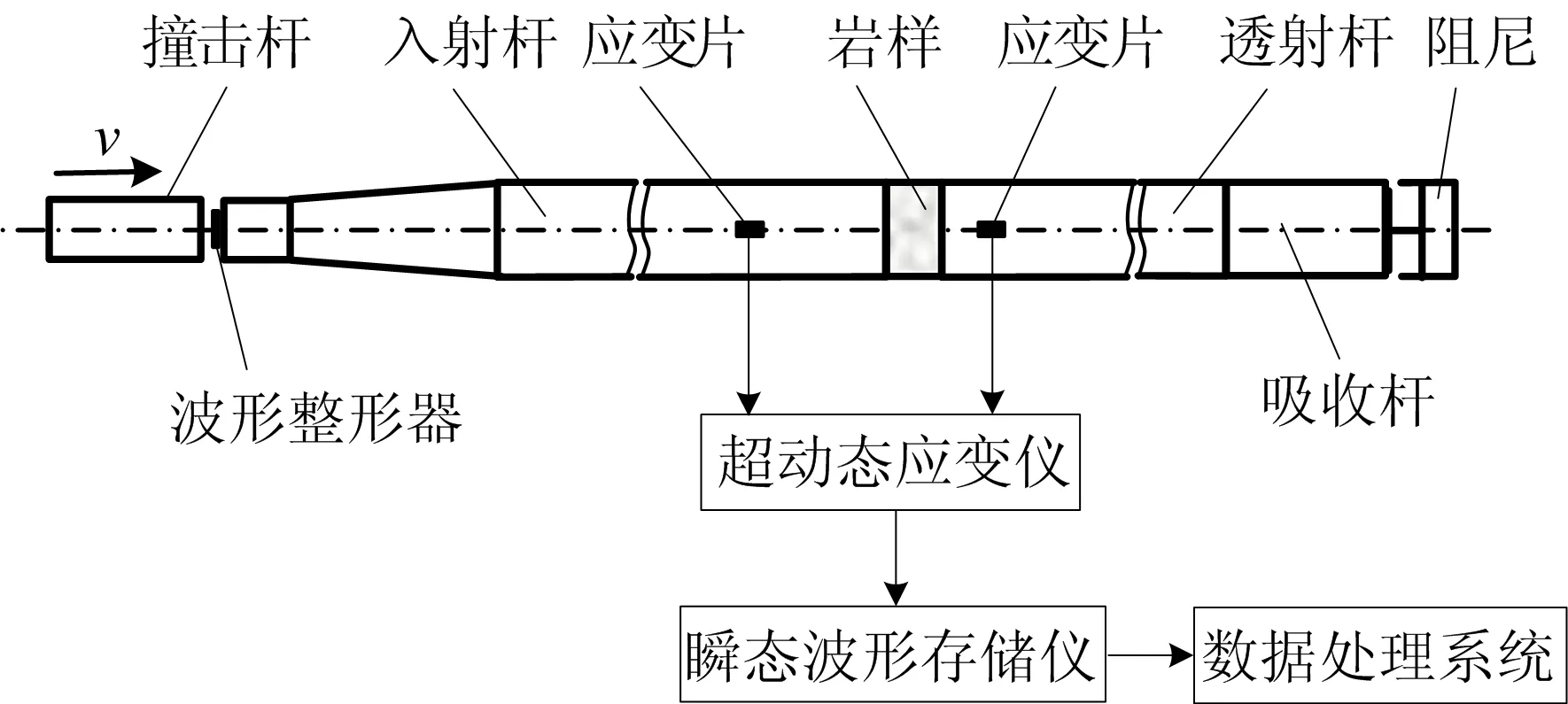
图1 直锥变截面SHPB装置冲击压缩试验简图
(1)
其中:C、E、A分别为压杆(入射杆和透射杆)的弹性波波速、弹性模量及横截面面积;ls、As分别为岩样的长度和横截面面积。εi(t)、εt(t)均统一以岩样处为时程起点,则σdc(t)和εdc(t)消去时间轴即为岩样的应力-应变关系(曲线)。为了便于分析,每个岩样的应变率为其应力-应变曲线上升段的平均值。
2 试验结果及分析
对不同种类、不同长度的6组别岩样进行了4个应变率的冲击压缩试验,每个应变率下同组别岩样2~3个。
2.1 试验结果
(1) 岩样的应力-应变曲线及破坏形态。因为相近应变率下同组别岩样的应力-应变曲线相差不大,所以6个组别岩样1个应变率仅给出1条代表性曲线,如图2~图4所示。第2撞击杆速度(v=16.5 m/s)下6个组别岩样的破坏形态如图5所示。

图2 不同应变率下长径比0.5岩样的应力-应变曲线
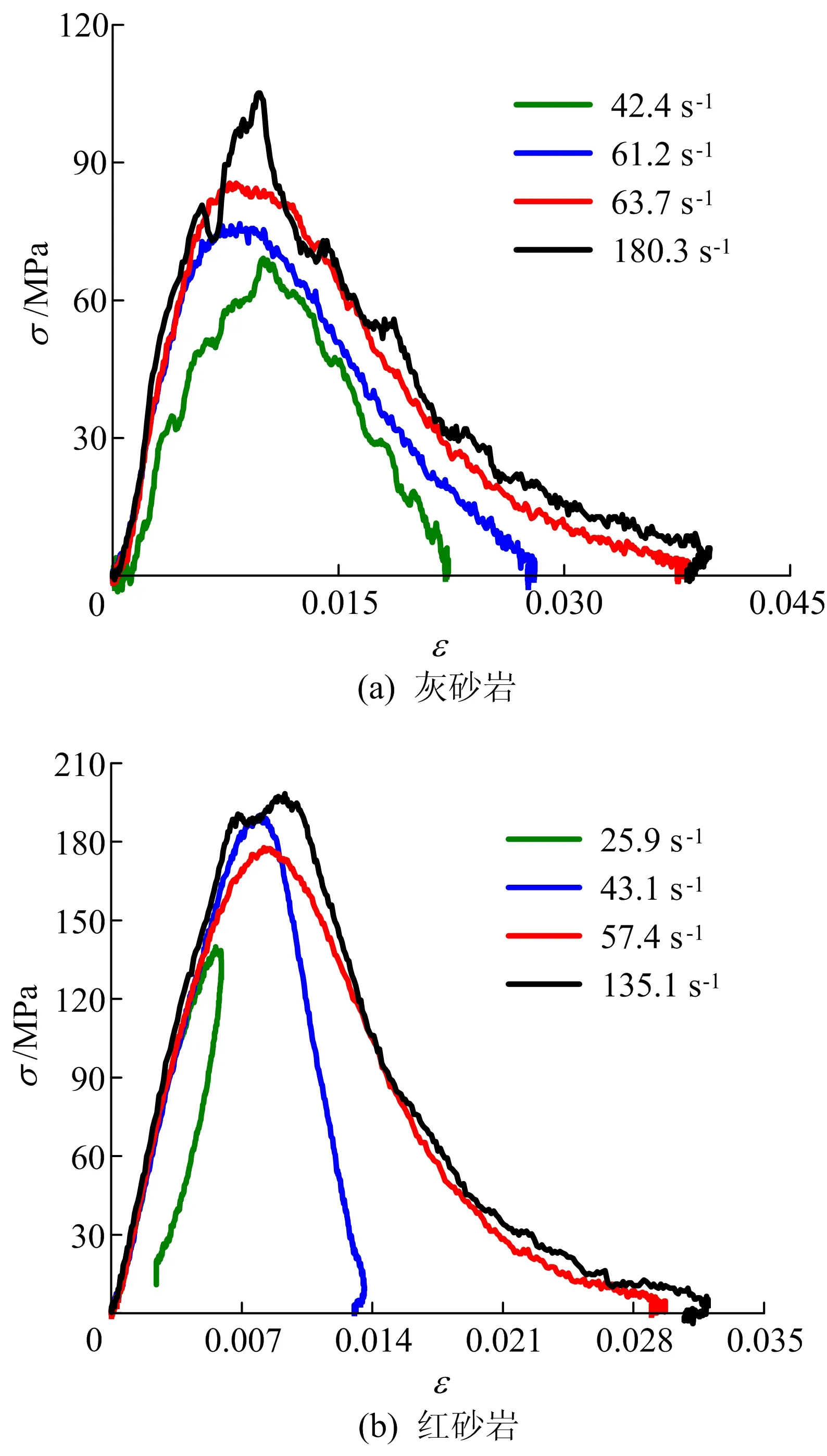

图4 不同应变率下长径比1.5岩样的应力-应变曲线

图5 撞击杆速度v=16.5 m/s下不同尺寸岩样的破坏形态
(2) 不同应变率下岩样的抗压强度。将相近应变率的相同组别岩样的应变率及动态抗压强度fdc平均,结果见表2所列。

表2 不同应变率下6组岩样的fdc
2.2 分析
2种砂岩的fsc随长径比的变化规律如图6所示。
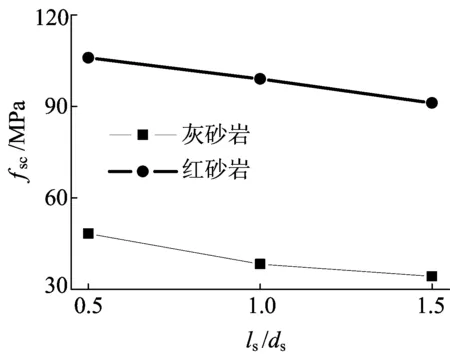
图6 2种砂岩fsc随长径比的变化规律
由图6可知, 2种砂岩的fsc均随长径比的增大而线性降低,相同长径比下灰砂岩降低的幅度略大于红砂岩。因为试验机压头直径仅略大于岩样,岩样端面进行磨削加工,且与压头接触面涂抹了润滑剂,综合看摩擦影响较小,所以岩石fsc的尺寸效应不仅仅是摩擦效应导致的。
由图2~图4可知:
(1) 随应变率增大,6组岩样的动态抗压强度基本增大,即砂岩强度具有显著的应变率增强效应。
(2) 随应变率增大,6组岩样应力-应变曲线的弹性段增长,弹性模量略有增大,塑性强化段增长变陡,破坏卸载段初期变陡、后期发散,即具有应变率增脆和破坏体积扩容增大效应。
(3) 不同长径比岩样的力学行为随应变率的变化规律不一致,长径比0.5时不同应变率下2种岩样应力-应变曲线整体均较光滑,当长径比增大时,随应变率增大,岩样应力-应变曲线的塑性段和卸载段出现显著起伏或波动,尤其是灰砂岩在塑性段会出现卸载后第2次加载现象。这种与试样长径比相关的行为应该与试验中岩样受力均匀性相关联,即随岩样长径比增大,惯性效应导致岩样沿轴向受力不均匀性显著。
从图5所示相同撞击杆速度下岩样不同的破坏形态也能看出这一特点:长径比0.5时岩样破碎颗粒均匀,随长径比增大,破碎颗粒不均匀性显著增大,甚至出现一端破损而一端未破损的情况。
为了定量分析尺寸效应对岩石fdc的影响,采用如下函数描述岩石fdc和fsc的比值——动态增强因子(dynamic increasing factor,DIF),即
(2)
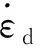
根据表1、表2的试验数据对(2)式进行拟合,拟合效果如图7所示,相关系数R2的范围为0.90~0.99。
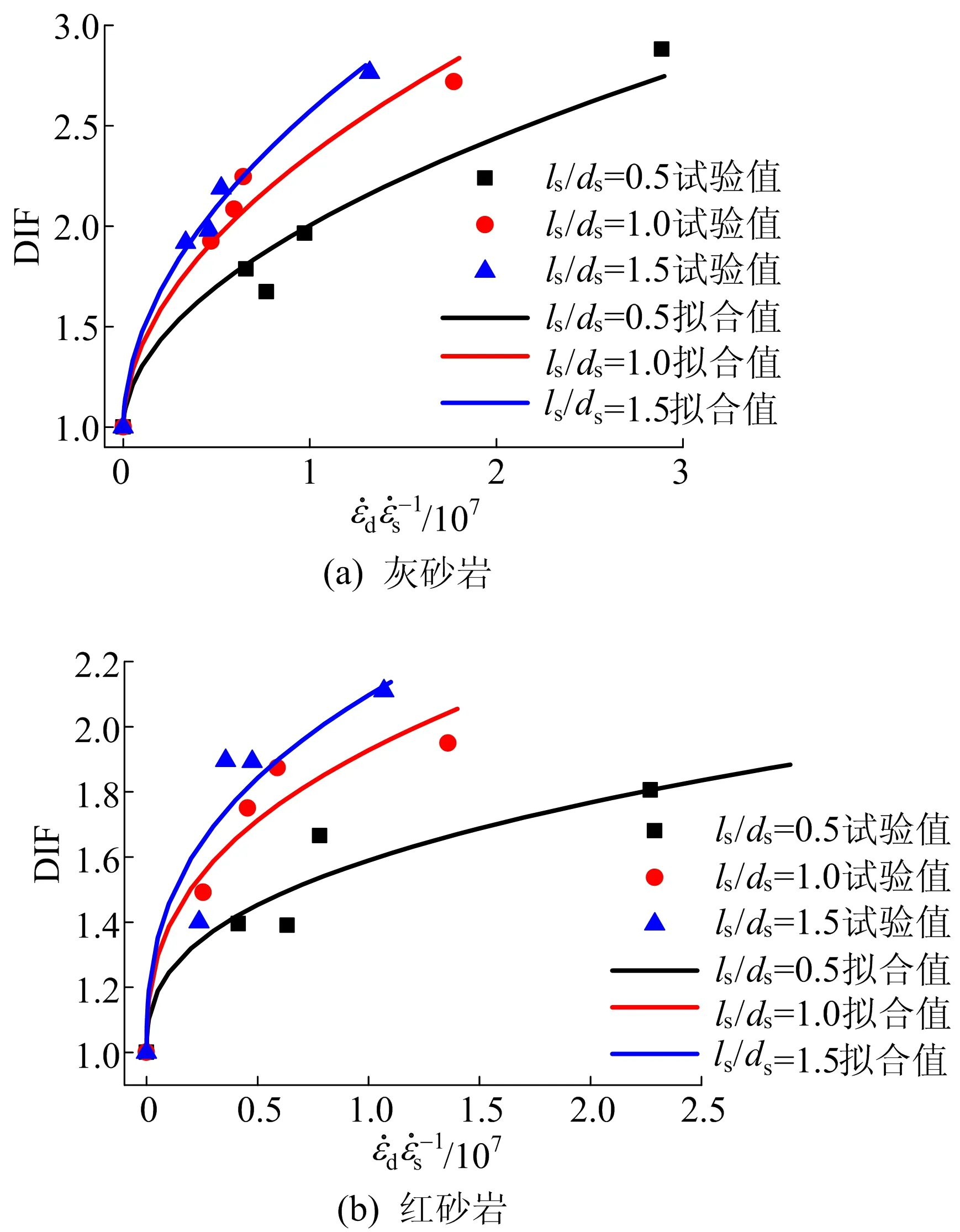
图7 2种砂岩DIF随应变率的变化规律
拟合得到的a、b值见表3所列。
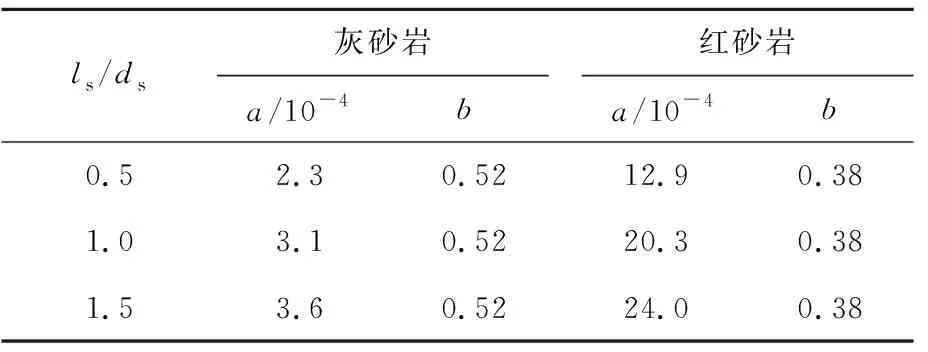
表3 2种砂岩不同长径比岩样的a、b拟合值
一方面,图7反映出(2)式较好地表示了2种砂岩fdc随应变率的变化规律。以往常用分段函数分别表示岩石准静态和动态强度随应变率的变化规律,则拟合函数在分段点处存在显著突变,其物理意义不明确。而(2)式可以统一反映岩石的静态和动态强度:当试验应变率趋向于准静态时,(2)式中的动态增强项很小,岩石强度趋向于静态强度;当应变率增大时,动态增强项的变化规律与大多数试验规律吻合。
另一方面,图7反映出尺寸效应也显著影响岩石的动态增强项,其影响规律不同于静态强度。
根据(2)式、图7及表3得到的主要结论有以下2点:
(1) 2种砂岩强度的动态增强项均随应变率呈幂函数增长,(2)式中的指数b仅与岩性有关,与试样的长径比无关,红砂岩的b低于灰砂岩,因此,随应变率增加,红砂岩的增强效应低于灰砂岩。
(2) (2)式中的系数a同时与岩性、长径比相关,其随岩样长径比的变化规律如图8所示。从图8可以看出,2种砂岩a值均随试样长径比增加而增加,但灰砂岩增加速率低于红砂岩。这说明对于某一种岩石,长径比越大,强度动态增幅越大,而对于这2种砂岩,尺寸效应对红砂岩的影响大于灰砂岩。
综上所述,岩石DIF是静态强度、应变率效应、尺寸效应及岩性四者的耦合,如果静态和动态采用不同尺寸岩样进行试验,那么无法得到准确的DIF;而在动态试验中,岩样长径比越大,惯性效应的影响越严重。根据本文试验,岩样长径比0.5时2种砂岩在全部应变率下均表现出较好的受力均匀性,因此,建议在研究岩石动力特性时,无论静态和动态试验,岩样长径比统一选择为0.5。
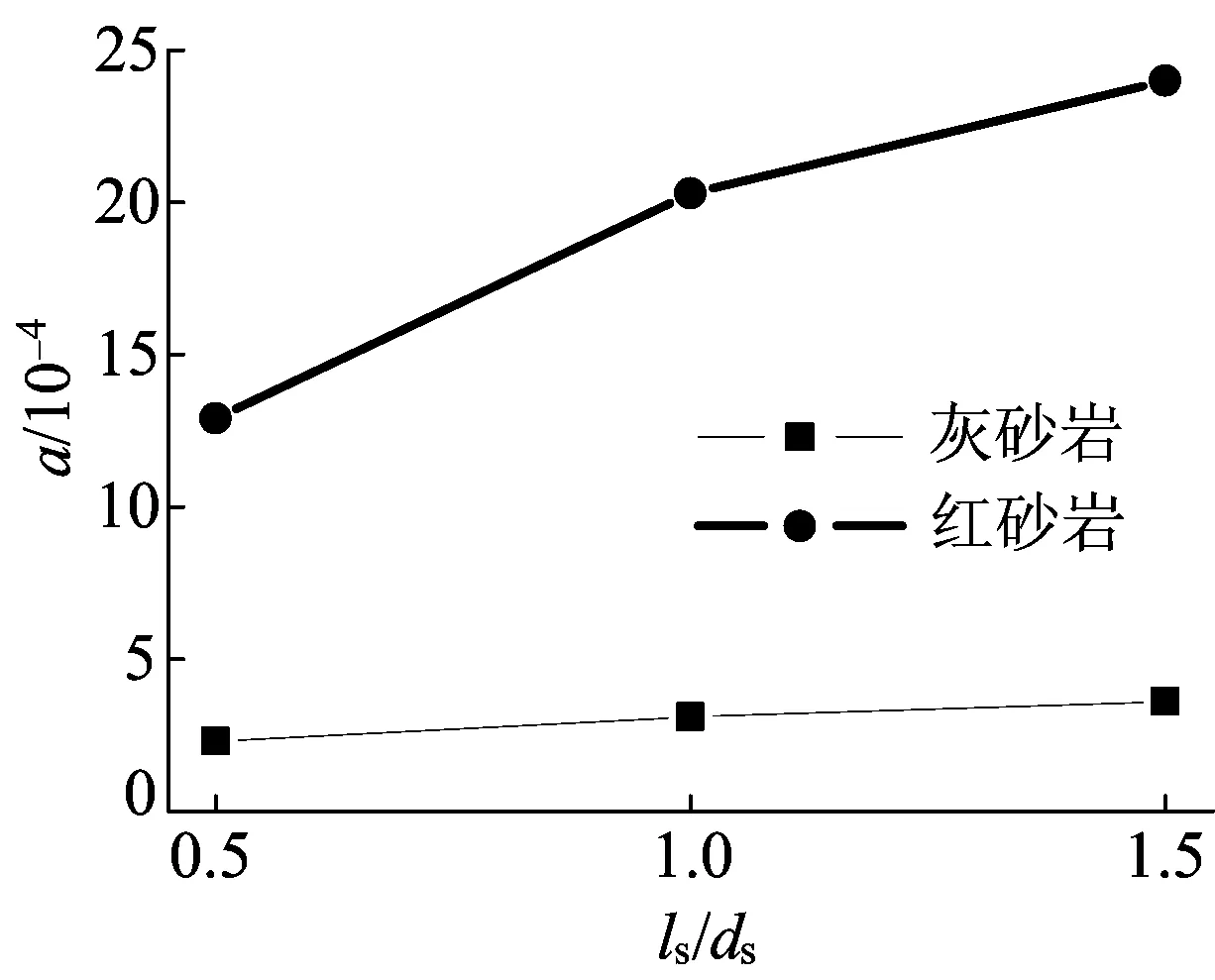
图8 2种砂岩的拟合系数a随长径比的变化规律
3 结 论
本文采用SHPB装置,对3种长径比的2种砂岩进行了4个应变率的动态压缩试验,主要结论如下:
(1) 静、动荷载作用下,岩石强度均存在尺寸效应,其中静荷载作用下岩石抗压强度随岩样长径比增大而减小,动荷载作用下岩石强度的动态增幅随岩样长径比增大而增大。
(2) 动荷载作用下岩石表现出显著的应变率增强效应,岩性、岩样长径比对岩石动态增强因子有耦合的规律性影响。岩样长径比越大,则岩石动强度增幅越大;岩石的强度越高,则尺寸效应的影响越显著。
(3) 动荷载作用下,由于惯性效应导致的岩样受力均匀性不同,岩石塑性强化段、破坏卸载段的变形特征也表现出尺寸效应的影响,为了让岩样在试验中尽快受力均匀,岩样长径比不能太大。
