基于非仿射随机波动模型对波动率互换的定价
2021-11-08贾兆丽张梦泽
刘 策, 贾兆丽, 张梦泽
(合肥工业大学 数学学院,安徽 合肥 230601)
金融衍生品在金融市场一直有很重要的地位,波动率衍生品是一种特殊的金融衍生品。近年来,人们对于波动率衍生品的关注度越来越高,当前金融市场最普遍的波动率衍生品就是方差互换和波动率互换。
随机波动率模型在金融计算中起到至关重要的作用,因为它可以描述金融资产收益率的波动的时变性、波动率聚集以及杠杆效应。金融计量文献中关于随机波动率模型的描述很多,最著名的是Heston模型。然而,Heston模型的波动率方程包含的平方根设定,虽然可以方便得到定价解析式,但忽略了金融时间序列的非线性特征,对于标的资产价格波动的描述比较片面。
文献[1]提出Heston随机波动模型;文献[2]基于变换方法,分析了3/2随机波动模型下的资产定价问题;文献[3]研究了Heston模型对于波动率产品的定价问题;文献[4]关注非仿射随机波动模型;文献[5]运用扰动法推导出风险中性测度下的标的资产对数价格lnST的特征函数;文献[6]对仿射和非仿射随机波动模型在资产配置影响、期权定价以及模拟分布等方面进行了研究,得出如下结论:非仿射随机波动模型在资产价格运动方面比传统的仿射型随机波动模型更好,可以使用仿射跳跃随机波动模型;文献[7]研究了OU随机过程下方差互换的定价问题;文献[8]的研究表明非仿射随机波动模型对于宏观经济的重要性;文献[9-12]表达了不同的随机波动率模型对波动率衍生品定价的影响。
本文假设标的资产价格服从非仿射随机波动率模型,因为非仿射随机波动率模型的标的资产对数价格分布的特征函数偏微分方程是非线性的,所以应用扰动法,将之前的非线性微分方程转化为线性微分方程,然后完成对离散采样波动率互换的闭解的研究。
1 波动率互换
波动率互换是一种远期合约,它在到期日的损益为:
(1)

(2)
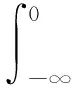
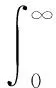
其中:T为合约期限;St为[0,T]时刻内标的资产的价格。假设St在[0,T]一共被观察了N次:t0=0≤t1 (3) 假设St表示资产价格的变动过程,它的瞬时波动率计为vt。在风险中性测度下,本文研究的非仿射随机波动率模型的形式如下: (4) 其中:r、k、θ、σ、γ均为正常数;r为无风险利率;k为波动率均值的回归速度;θ为资产收益波动率的长期均值;σ为资产收益率波动的波动率;W1t和W2t为2个标准的布朗运动,它们的相关系数均为ρ。 当γ=1时,(4)式是标准的Heston模型;当γ≠1时,(4)式是非仿射随机波动率模型。 对于特征函数,文献[3]给出了随机变量yt,T=lnST-lnSt(t f(φ;t,T,v0)=EQ[ejφyt,T|y0,v0] (5) 设当前的时间为0时刻,j为虚数单位,这个特征函数是解决本文定价问题的关键。本节接下来的主要任务是继续推导这个特征函数的闭解。 首先,根据条件期望的平滑性,(5)式可以表示为: f(φ;t,T,v0)=EQ[EQ[ejφyt,T|yt,vt]|y0,v0] (6) 其中,0 假设(6)式内部的期望具有解的形式:g(φ;s,T,ys,vs),t≤s≤T。令τ=T-t,由Feynman-Kac定理得: (7) 边界条件为: (8) 显然,(7)式是一个非线性偏微分方程,一般情况下,很难直接求它的解析解。 文献[5]提供了扰动法求解,可以将非线性偏微分方程转化为线性偏微分方程,以便求解。将v(γ+1)/2和vγ在v=θ处进行一阶泰勒展开,可得: (9) vγ≈θγ(1-γ)+γθγ-1v (10) 将(9)式、(10)式代入(7)式,可得: (11) 此时,(11)式是一个线性偏微分方程;接下来,对(11)式采用待定系数法求解。特征函数g(φ;s,T,ys,vs)有如下形式: g(φ;s,T,ys,vs)=eC(τ)+D(τ)v+jφyt,T (12) 将(12)式代入(11)式,整理得: (13) (14) (13)式和(14)式是2个常微分方程,分别求解得: C(τ)=jφrτ- (d-g)3e-dττ-4d(d-g)(1-e-dτ)]} (15) (16) 若t=T,则yT,T=lnST-lnST=0。 于是,可以求出(6)式的内部期望。接下来,特征函数可变为: f(φ;t,T,v0)=eC(τ)EQ[eD(τ)vt|v0] (17) 不妨令h(φ;t,T,s,v0)=EQ[eD(τ)vt|v0],0≤s≤t,再由Feynman-Kac定理得: (18) 边界条件为: (19) 根据文献[1],可假设h(φ;t,T,s,v0)具有仿射形式的解: (20) 将(20)式代入(18)式,可得: (21) (22) 分别求解常微分方程(21)式、(22)式,可得: (23) (24) 于是,特征函数f(φ;t,T,v0)中的关键问题都得到了解决。 最后,令s=0,对f(φ;t,T,v0)的表达式进行整理,可得: f(φ;t,T,v0)=eC(τ)EQ[eD(τ)vt|v0]= (25) 于是得到随机变量yt,T=lnSt-lnST(t 由(3)式不难发现,计算Kvol的关健是求解表达式: (26) 根据文献[3],波动率互换的已实现波动率(26)式为: (27) 其中:p(yti-1,ti)为随机变量yti-1,ti的向前密度函数;q(yti-1,ti)=eyti-1,ti-r(ti-ti-1)p(yti-1,ti)为它的概率密度函数。因此 (28) 另一方面, (29) 再根据2.2节对特征函数的计算,得到波动率互换的定价公式,即 (30) 于是,在非仿射随机波动率模型下,对波动率互换的定价就完成了。 随机波动率模型下的金融资产的定价问题已经成为学术界的热点,传统的仿射型随机波动模型虽然处理问题有许多便利之处;但实验表明,非仿射随机波动率模型比传统的随机波动模型能更好地描述资产价格的运动。基于传统波动率模型的处理经验,可利用扰动法将非线性偏微分方程转化为线性偏微分方程,再进行求解,最后利用傅里叶变换的原理对波动率期权进行定价。 非仿射随机波动率模型具有更一般的资产价格描述。未来,可以利用该模型给更多的金融资产进行定价。此外,还可以将扰动法进行改进,或将反馈原理引入到非仿射随机波动率模型中,或在技术层面上,通过改进的扰动法的泰勒展开近似表达式,进一步提高该模型的定价性能。
2 波动率互换的定价
2.1 模型建立
2.2 特征函数的推导
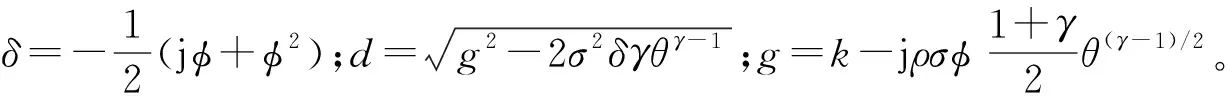
2.3 定价过程

3 结 论
