抽水蓄能电站输水隧洞无人机自主飞行技术研究
2021-11-07赵毅锋沈润杰
李 晓, 沈 浩, 赵毅锋, 黄 浩, 沈润杰, 郭 帅
(1.华东天荒坪抽水蓄能有限责任公司,浙江 安吉 313302; 2.同济大学 电子与信息工程学院,上海 201804; 3.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
0 引 言
抽水蓄能电站高压引水隧洞在高速水流的不断冲刷过程中,存在被冲蚀的风险;抽水蓄能电站输水道普遍长度长、角度大,现阶段输水道在无水情况下通常利用台车和蜘蛛人检查,有水情况下通常采用水下机器人检查,但这些检查手段普遍存在安全风险高的问题,且不适合具有分段水平洞和垂直隧洞情况,因此开发新型的输水道系统检测技术迫在眉睫。
近年来,随着传感器技术和无人机技术的快速发展,利用多旋翼无人机搭载采集设备进行隧道内部的快速检测成为可能,但隧道内部存在GPS信号屏蔽和地磁干扰现象,对无人机的自主飞行带来技术挑战。国内外研究者针对无人机在封闭空间内的自主飞行做了大量的研究,取得了较丰富的成果。文献[1-2]开发了利用多旋翼无人机进行工业烟囱巡检的无人机导航系统,该系统搭载了多个传感器,包括轻型3D激光扫描仪,用于无人机的导航和避障;文献[3]尝试采用视觉、二维激光雷达、三维激光雷达等不同传感器组合进行大坝管道内的无人机位姿估计;通过搭载惯性传感器、2个单线激光雷达及4个相机的水坝管道巡检无人机,文献[4-5]提出了依赖管道圆柱几何形状的融合惯导、激光雷达、摄像机的六自由度估计算法,该算法利用Velodyne16线激光雷达、惯性测量单元(Inertial Measurement Unit,IMU)、4个摄像头进行无人机六自由度位姿估计,该系统具有一定的自主导航和构建局部环境地图的能力;文献[6]提出了基于三维激光雷达的位姿估计算法,该算法采用Velodyne16线激光雷达,通过在非线性流形上的优化过程重建以无人机为中心的局部地图,并通过卡尔曼滤波器优化最终的六自由度状态估计,可以适应不同直径、横截面及不同弯曲程度的管道环境,如图1、图2所示。

图1 无人机在大坝管道中的飞行实验

图2 基于三维激光雷达算法的管道局部地图
在国内,对于无人机在室内、隧道内等无GPS信号空间内的自主导航技术也有一些研究报道。文献[7]研究了基于单目视觉的无人机室内导航方法;文献[8]设计开发了面向隧道内的自主侦查无人机系统;文献[9]研究了针对小型无人机在无卫星导航信号条件下的导航问题;同济大学无人机开发团队利用单线激光雷达融合IMU和气压计等实现了隧洞的自主飞行技术,并于2019年首次对天荒坪、桐柏抽水蓄能电站进行自主飞行,获得成功。
本文研究四旋翼无人机在无GPS信号环境中的自主导航方法,提出了基于三维激光雷达、惯导、气压计的多传感器融合无人机位姿估计算法,实现了无人机在电站输水隧洞内的智能感知和自主飞行。仿真模拟和实验结果表明本文位置控制算法的有效性。本文研究成果可为抽水蓄能电站输水隧洞无人机检测技术提供参考。
1 基于隧洞圆形特征无人机定位方法
考虑到抽水蓄能输水隧洞为圆形特殊工业环境,其隧道的纹理特征贫乏,结构特征重复,难于用传统的激光雷达测距与建图 (LiDAR Odometry and Mapping,LOAM)或视觉的方法对无人机进行定位,本文提出一种基于隧洞圆形特征(曲率、法线及圆心)的无人机定位方法。无人机在飞行时,对于路径规划和最优路径的选取,都相对圆心来确定自身位置的定位。因此,本文采用圆心算法——Hough变换[10]和对最小二乘法进行优化的Levenberg-Marquardt算法提取圆面特征。
随机Hough变换提取圆的基本原理是随机采样3个点来确定一个圆。检测圆心坐标,是根据圆的几何性质,即圆心为圆周上任意两条不平行弦的中垂线的交点来确定。点云拟合求解圆心示意图如图3所示。
最小二乘法求解圆心坐标原理如下。设圆周上有n个点,任意2点坐标为(xi,yi)、(xj,yj)(0 (xi-a)2+(yi-b)2= (xj-a)2+(yj-b)2 (1) 可以列出n-1个方程的方程组,简化成矩阵表达式为: V=Ax-l (2) 其中,A、x、l分别为: (3) (4) (5) 图3 点云拟合求解圆心示意图 V(Tδ+ΔTδ)≈V(Tδ)+J(Tδ)ΔTδ (6) 其中,J(Tδ)为V(Tδ)的雅克比矩阵。 Levenberg-Marquardt算法通过比较近似模型和实际函数之间的差异来确定ΔTδ的可信赖范围,给定近似范围μ,其增量方程为: ‖Tδ‖2≤μ (7) 增量方程是带有不等式约束的优化问题,用拉格朗日乘子λ将其转化成无约束优化问题,即 (8) (8)式可以通过对ΔTδ求偏导,逐步迭代求解。 而对于法线,通过最近邻(k-nearest neighbors,KNN)算法计算无人机激光雷达采集的点云,通过邻近点云计算出小区域的平面,从而获得相应的法向量。 在四旋翼无人机的位姿控制中,以电子罗盘、IMU及气压计等传感器为基础的互补滤波姿态和高度估计算法相对成熟。通常以陀螺仪为主,用加速度计来辅助检测无人机的俯仰角和滚转角,使用电子罗盘修正无人机的偏航角,使用气压计修正无人机的高度。其算法框架如图4所示。 图4 基于多传感器融合的位姿估计算法框架 四旋翼无人机姿态解算是将陀螺仪、加速度计及气压计等测得的数据进行融合得到姿态角的。陀螺仪测得的数据本身存在温漂和零漂误差,导致在长时间探测时具有较大的误差,而加速度计不具备良好的动态能力,因此单独使用加速度计或陀螺仪不能精确地进行姿态解算,需要对陀螺仪数据和加速度数据分别进行高通滤波和低通滤波,并将滤波后的数据进行融合求解,从而提高姿态解算精度。基于互补滤波器的滚转角、俯仰角算法流程如图5所示。 图5 基于互补滤波器的滚转角、俯仰角算法流程 通过IMU和气压计获得无人机的3个自由度(滚转角、俯仰角及高度)的相对准确值后,还需要估计水平方向位置和偏航角。对于偏航估计,同样可以分为特征提取、特征匹配与运动估计、位姿优化3步,基本原理相近,仅在算法上,由于已知部分姿态信息,会有一些差别。以t1~t2时间段内激光雷达的运动估计为例,假设已知在该时间段内x、y方向的运动增量和t1时刻的偏航角,在未知部分姿态的情况下,是以上一次估计的运动增量作为本次运动增量的估计值进行转换。在已知滚转角、俯仰角及高度情况下,可以更精准地转换。 根据当前时刻和上一时刻的高度,可以求得高度方向的运动增量,进而可以通过坐标转换关系反求得平移增量。由于在无人机飞行过程中,无人机的偏航角变化不大,可以假定当前无人机的偏航角与上一时刻相同。 本算法考虑隧洞工业环境的特殊性,作出如下假设: (1) 隧道本身呈规则形状,即本身的立体空间是以立方体、圆柱体及球体为核心的组合空间体。 (2) 隧道表面不存在剧烈不规则形变,隧洞管道的平面特征可以粗略获取。 (3) 无人机在过渡段不会有横截面积的突变。 无人机自主飞行的机载传感器(加速度计、气压计、IMU、激光/红外测距仪等)中,在位置控制算法中需要涉及的传感器主要以16线激光雷达为主,激光/红外测距仪作为辅助手段。通过转换关系将无人机坐标转换为世界坐标。通过16线激光雷达对前侧有明显线、面特征转变的面进行处理,获得该面的法向量,同时在无人机前进方向和通过机身的法向量形成的平面上做法向量的垂线,以保证无人机在飞行时相对底部障碍物的距离为恒定高度,即轴心飞行。 当无人机进入水平激光雷达点云图呈封闭图形时,认为无人机进入了工作段,即无人机飞行下一时刻的位置坐标可以通过前一时刻的位移增量来估计,或者可以通过激光点云图计算出其特征轴线或特征中心作为下一时刻的飞行位置。 仿真实验的主要目的是通过仿真获得无人机在各种特殊工业环境中的最佳飞行路径和特殊路径过渡优化,同时要考虑在不同环境中激光点云的建图效果和位置估计精度。本文借鉴多传感器融合的位姿估计算法,提出针对特殊立体的法线、轴线来优化无人机过渡段飞行稳定性算法,并通过仿真模拟来验证算法的有效性。 本文的仿真系统运行在无人机操作系统(Robot Operating System,ROS)下,由PX4仿真飞控、自主飞行系统及Gazebo仿真模型3部分构成,仿真系统框架如图6所示,三维管道模型如图7所示。 图6 无人机位姿仿真系统框架 图7 引水隧道Gazebo模型 PX4是当前最流行的开源飞控板之一,其本身是一个Firmware软件系统,以Nuttx实时ARM系统为核心操作系统,内含Gazebo中使用的传感器驱动程序,通过传感器输出信息到飞控程序,最后转化为电机转速,输出到仿真环境。在本文中,通过IMU、气压计、激光雷达等计算无人机当前的位置姿态信息,并将其发布在ROS话题中。 隧洞三维点云地图如图8所示。在点云图成像上,因为飞行不平稳和水平段长度的影响,点云成像会有一定的偏移,但当无人机飞行至邻近区域时,会对错误点云信息进行自纠正,所以该偏移不影响无人机本身的飞行。从飞行路径来看,无人机在圆柱形管道中的飞行路径有一定量的累计误差,同时在到达过渡目标点周围时,无人机会在周围减速,逐步抬高自身位置,进入到斜飞段或垂直段。 图8 隧洞三维点云地图 无人机仿真飞行过程中的y方向世界真值与仿真预测值对比如图9所示。 图9 y方向位姿世界真值与仿真值对比 从图9可以看出: (1) 在整体趋势上,世界真值与仿真值保持了高度的一致,能够精准描绘出隧洞环境各位置的信息变化和趋势。 (2) 仿真值与世界真值相比整体偏小,这在一定程度上避免了无人机发生碰撞,降低了无人机坠机的可能性,但从最后应用于检测环境来看,会损失一定的精度,因此还存在一定的优化空间。 偏航角对于无人机在隧洞内的飞行至关重要,偏航角世界真值和仿真值对比如图10所示。从图10可以看出,无人机在仿真飞行过程中两者变化的趋势高度相似,但其仍然存在以下2个问题: 问题1 偏航角仿真值的波动非常明显,虽然波动范围较小,但仍然会使得无人机在飞行过程中存在不断左、右偏斜的问题,不利于无人机的稳定飞行和实际工作环境中对于需要检测位置的锁定。 问题2 仿真值整体偏大,这会导致在实际飞行过程中存在过补偿的问题,而过补偿的问题会直接导致无人机不断纠正自身的偏航角,因而产生问题1。因此,需要对无人机飞行过程中的偏航角进行精准计算和拟合,以确保无人机在隧洞类环境飞行过程中的安全性、稳定性。 图10 偏航角世界真值与仿真值对比 3.3.1 位置精度分析 因垂直段飞行立体空间具有特殊性,位置估计结果取另一次仿真实验中倾斜段的数据进行分析。无人机在倾斜段飞行的轨迹如图11所示。将在局部坐标系下估计得到的局部位置,通过无人机的高度和管道倾角转换到全局坐标系中,作为位置参考。 图11 倾斜段飞行轨迹 从局部坐标位置可以看出在切换飞行模式之后,无人机逐渐运动到局部坐标系的原点并一直保持在原点附近,对应了管道的中轴线。多传感器融合算法输出的位置与局部坐标估计转换到全局坐标后的结果基本吻合,两者之间的偏差最大不超过0.5 m。 3.3.2 速度精度分析 无人机飞行过程中轴线速度的仿真值与世界真值对比如图12所示。从图12可以看出:两者的误差在0.2 m/s之内;世界真值波动较大,但在可接受范围之内。两者误差较小,表明无人机飞行可以得到精准控制。 图12 仿真轴线速度仿真值与世界真值对比 在某水电站引水隧洞进行无人机实地飞行实验。当无人机进入倾斜段时,考虑到点云信息已经是完整的圆,沿轴线飞行意味着x、y方向速度期望均值为0 m/s。 实际采集的倾斜段x、y方向速度部分数据如图13所示。 从图13可以看出,在无人机实际飞行过程中,x、y方向上的速度均值分别为-0.031、0.017 m/s,与预期速度相符;斜段速度以0为均值上、下波动,最大的波动分别为0.3、0.2 m/s。 图13 倾斜段实测x、y方向速度 (1) 从无人机飞行点云图成像可以看出,激光雷达的成像与实际飞行环境的情况之间存在一定的误差,会出现点云偏离成像,但当无人机位置与管道壁相对较近时,激光雷达的成像会自行纠正本身的错误成像。激光雷达的偏离成像会在一定程度上干扰无人机在过渡段的飞行,但控制无人机自身的飞行速度可以将错误成像的影响降低,实现较为精准的飞行路径规划。激光雷达成像在垂直方向仰角的限制,会导致激光雷达成像并不封闭,观察激光雷达成像,在圆柱管道仿真环境内飞行上方成像缺失,但其本身并不影响无人机的飞行,可以忽略。 (2) 无人机在隧洞类仿真环境中的飞行,其路径、飞行速度、位姿估计等输出结果与世界真值比较,误差均在可以接受范围之内,表明本文提出的算法能够高效、安全地解决无人机在缺乏GPS信号、受地磁干扰、光照不足条件下的隧洞类环境中的自主飞行问题。


2 基于多传感器融合的无人机姿态估计
2.1 框架设计

2.2 俯仰角、滚转角及高度估计

2.3 水平方向位置和偏航角估计
2.4 过渡段算法逻辑
2.5 倾斜段、垂直段飞行
3 隧洞无人机位姿估计仿真及实验
3.1 仿真系统框架设计
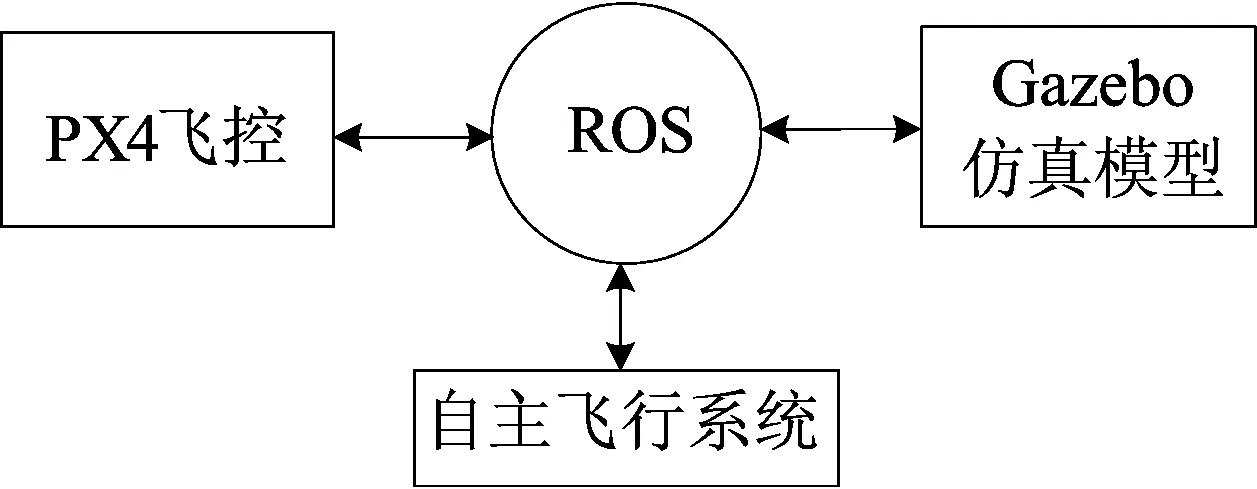

3.2 仿真结果及分析



3.3 控制精度分析


3.4 实地实验结果分析
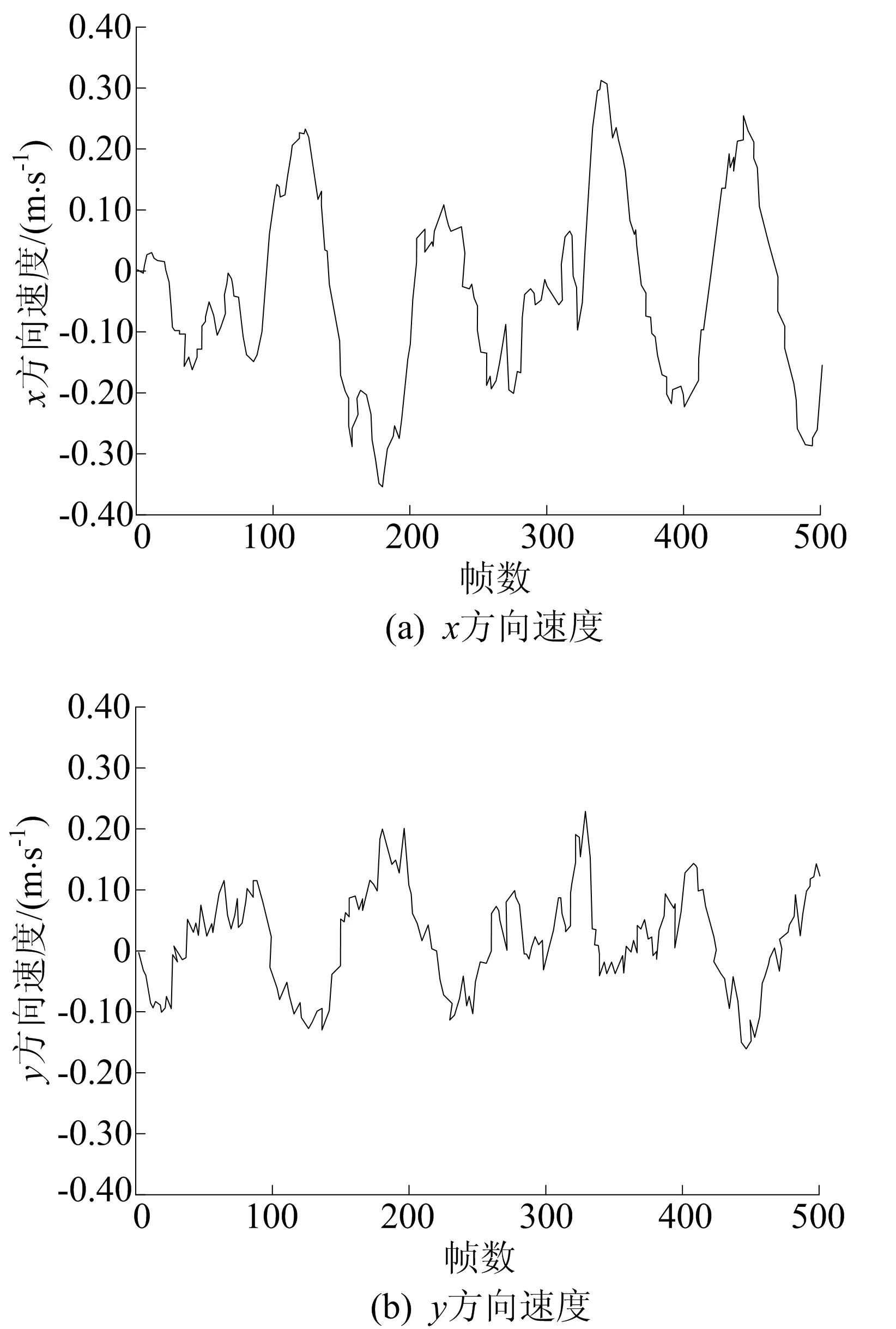
4 结 论
