基于两级排队系统的农产品拍卖分货人员优化配置

缪 彬，伊雅卉

（昆明理工大学 管理与经济学院，云南 昆明 650093）

0 引言

荷兰式拍卖是在公开场合通过竞价转让所有权的现代交易模式［1］，是一种常见的价格形成与资源分配机制［2］，拍卖交易具有速度快、批量大、公平公开等特点，能够有效提高效率、降低成本.我国在上世纪80年代末开始探索农产品拍卖交易，目前已经有K鲜切花拍卖市场等较为成功的案例.本文以K鲜切花拍卖市场作为研究对象，由于国内鲜切花“小农户、大市场”的产业现状，鲜切花拍卖交易形成了“批次多、批量小”的特点.拍卖完成后需要按照交易结果进行分货、归集、提货等操作，使得拍市拍后物流运作较为复杂、工作量大，其中分货效率关系到整个拍卖市场的服务能力和服务质量.将完成交易需要进行分货处理的货物视为“到达顾客”，分货人员是“服务台”，分货过程则是服务台的服务过程，拍市的分货问题可以视作一个排队问题.为了解决K鲜切花拍卖市场拍后物流分货人员的配置、效率及成本优化问题，本文建立两级排队模型，考虑成本与效率，实现人员优化配置的目标.

近年来，应用排队系统模型对服务台进行优化配置的研究中呈现两个方面的趋势：一是通过服务台数量变化来改善排队系统模型中的运作参数指标，确定最优服务台数量；二是将排队系统模型中参数指标与成本收益相结合，得到服务台的优化配置方案.

在通过变化服务台数量优化运作参数指标方面的文献，通过计算平均到达率和平均服务率，统计排队系统的各项参数指标，观察指标的变化情况，确定最优服务台数量.Xie［3］收集机场实际人流量数据，结合提高机场安检服务效率和质量的目标，确定最优安检点数目.蒋辰等［4］研究了高校图书馆的排队系统，将排队和工作人员空闲的概率控制在一个可以接受的范围内，收集现有数据，预测未来读者到达量与借还书量，确定高峰期、非高峰期时最优人工和自助借还书台数量.宫宇姝［5］建立了兰州客运西站铁路购票、安检的两级排队系统模型，根据窗口的运用效率确定是否增设取票窗口和安检设备.李建国等［6］建立了自动化立体车库的排队理论模型，设计车库库位不同层和列的组合、堆垛机数量方案，对不同方案的平均等待时间和等待队长进行横纵向比较，确定最优层、列和堆垛机数量.陈中武等［7］对排队系统的队长进行限制，结合遗传算法，计算服务台增加后，种群参数变化情况，得出最优解，确定最优设施与服务台数量方案.在这些研究中，不同的排队系统中都存在服务台数量少这一相同的“瓶颈”，增设服务台数量后，服务效率提高.

在通过改变服务台数量平衡成本与效率方面的研究，多集中于医院和客运站等人流量较大、较易产生排队现象的场地.林培群等［8］以高速公路收费站运营成本最小为优化目标，统计排队系统中各项参数计算系统延误成本，并结合灵敏度分析来确定最终的优化方案.Agyei等［9］将银行服务窗口问题抽象为一个排队系统模型，建立总成本最小化的目标函数，确定最佳窗口数量.赵书强等［10］基于城市道路信息、在充电站充电的电动车数量，综合考虑建设成本、行驶成本及等待成本等，确定充电站的选址、布局和数量.吴晓丹等［11］通过建立社区服务中心疾病筛查的排队理论模型，提出社区间共享医师或增加筛查设备两种优化模式，计算投入成本，得出最优联合筛查方案.Kemb等［12］、朱明珠等［13］、李凌洋等［14］、吴玲等［15］对医院门诊、取药的排队系统进行研究，建立成本函数使患者排队的等待成本和医院的经营成本最小，确定最优收费窗口数量的优化方案.李得伟等［16］、任其亮等［17］研究了铁路客运枢纽的出租车排队系统，根据到站乘客对出租车的数量和换乘时间的需求建立排队系统模型，以总费用最小为目标，确定最佳泊位数量.从上述研究可以看出，在增加服务台数量的同时计算运营成本、延误成本等的变化情况，可以达到服务台数量增加，服务效率提高而成本降低的优化目标.

综上所述，国内外学者对建立排队理论模型确定最优服务台数量的研究成果较为丰富，目前应用于交通、物流、仓库、医院、银行、餐饮等众多领域，对服务台的优化配置有效的提升了企业的管理水平和运营效率.但目前的研究主要都集中在单级排队系统，对业务之间有衔接、需要连续排队的多级排队问题的研究成果不多.本文在此基础上，结合K鲜切花拍卖市场的运营实际，将拍市拍后分货物流的两级分货服务看作一个两级排队系统，建立拍后分货的两级排队系统模型，综合考虑效率和成本，确定优化运营方案，实现提升拍市的服务质量与经济效益的目标.

1 问题描述

K鲜切花拍卖市场采用荷兰式降价拍卖交易模式，在交易效率方面有突出优势，目前K拍市有六口交易大钟同时进行拍卖，每口钟的平均交易速度到达3.6 s／批次，六口钟平均每分钟可以完成约100笔交易，交易效率极高.拍卖以列为排序单位、批次为交易单位、桶为成交单位，同一批次的鲜切花可以被不同的购买商购买，购买商也可以参加任意批次的竞拍，购买量取决于购买商需求.由于购买商数量多、交易批量小、交易批次多，所需分货场地面积大，给拍后分货造成较大的工作量.如果采用“直接分货”，即一次性将购买商购买的鲜切花送至最终提货位置的方式，使得分货员在场地中行走的路程较长，加之一时难以找到对应的货位，导致重复行走时间的增加.为了提高分货效率，减少分货员的重复行走，拍市目前采用“两级分货”的方式，每个购买商在一次分货区有一辆台车大小的货位，二次分货按购买商进行货品归集，货位大小根据购买商交易量进行调整.台车拍卖完成后，交易系统根据拍卖结果自动分配两次分货的货位，并打印分货单，分货员根据分货单将货品送往一次分货区，存储量满一台车后送往二次分货区进行货品归集，等待购买商提货.具体分货流程如图1所示.

图1 拍市分货流程图Fig.1 Flow chart of auction market distribution of goods

拍市的场地被分为拍卖大厅、待拍区、缓冲区、一次分货区、二次分货区、出货扫描区和提货区，由于二次分货区是在分货进行一段时间，有购买商的存储量超过一辆台车后才会被使用到，为了节约场地建设成本、提高利用率，二次分货区和待拍区共用一块场地，场地布局如图2所示.

图2 场地示意图Fig.2 Schematic diagram of the site

经过长期的运作，拍市两级分货的方式满足了业务操作需要，为拍市服务质量的提升起到了保障作用，但随着效率的不断提升、交易批次的持续增加，目前拍市分货作业也产生下列问题：1）随着参与拍卖业务的拍卖师和购买商熟练程度不断提高，拍卖成交速度不断增加，一次分货速度跟不上拍卖速度，排队时长增加导致等待分货的队列占用通道，降低缓冲区的流通性；2）二次分货“前松后紧”，分货刚开始时，两次分货无法交叉并行，一次分货进行一段时间后二次分货才能开始，使得分货前段二次分货员空闲，整体分货时间延长，拍卖结束后工作又较为繁忙；3）提货等待时间过长，购买商只有在分货全部完成后才可以提货，长时间的等待加剧了购买商抱怨和不满的情绪.

通过对现场的考察和问题的分析，初步判断一次分货环节效率不高影响了整个分货作业的分货效率.从购买商的角度出发，分货员数量越多分货时间越短，购买商的等待时间越短；但从拍市角度来看，增加分货员数量在提高效率的同时，会使得总成本增加，为此需要对分货人员配置进行优化，平衡一次二次分货的效率及成本.

2 数据处理

本文利用SPSS 19.0软件对数据进行处理，主要包括以下几个方面：数据独立性检验、分布形式的判断、分布参数估计.通过数据分析判断台车到达时间间隔、分货服务时间所服从的分布，在此基础上建立两级排队理论模型，统计排队系统的各项运作参数指标，利用Flexsim软件对每级分货时长进行运营仿真，根据仿真结果计算两次分货总成本，得出最佳分货员数量.

2.1 数据采集

本文以台车拍卖结束的时间为台车到达排队系统的时间，故从交易系统中提取每辆台车拍卖完成时间计算台车到达时间间隔.由于每口大钟独立分货，分货员数量相等且分货效率基本相同，为降低数据采集的难度，在数据采集的过程中选取一口大钟为数据采集对象，随机选取了4个工作日，对拍市分货员工作时间进行统计.经过整理，台车到达时间间隔和分货服务时间数据情况分别如表1和表2所示.

表1 台车到达的时间间隔Tab.1 Trolley arrival time interval

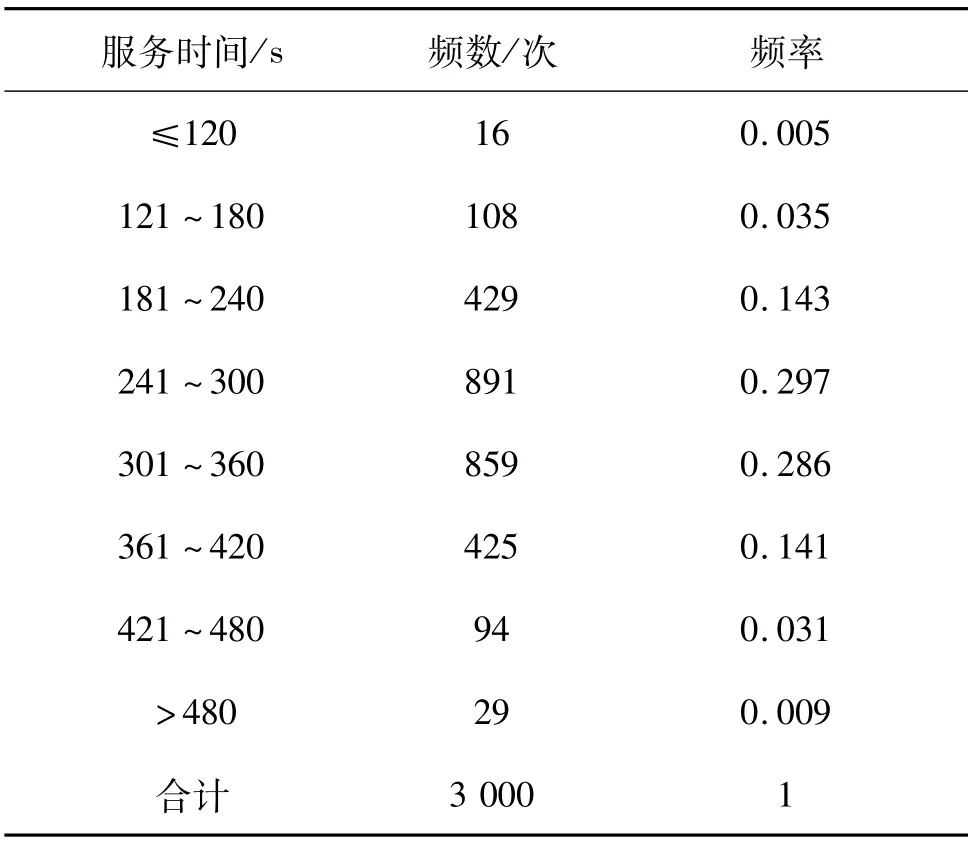
表2 分货服务时间Tab.2 Distribution time

2.2 数据的独立性检验

在对采集到的数据进行分析之前要先进行独立性检验，如果数据独立则进行下一步的分析，不独立则数据无效.根据测得的数据，绘制出相关的散点图进行独立性判断.

如图3和图4所示，观察台车到达时间间隔和分货服务时间的散点图，数据随机散布在平面直角坐标系内，没有明显的变化趋势，可以判断样本数据是独立的.

图3 台车到达时间间隔的散点图Fig.3 Scatter plot of trolley arrival time interval

图4 分货服务时间的散点图Fig.4 Scatter plot of distribution time

2.3 数据分布形式的假定

以数据值为横坐标，频数值为纵坐标，绘制频率分布直方图，初步判断数据的经验分布情况.

如图5和图6所示，观察直方图，可以看出到达时间间隔与服务时间均呈现先增后减的趋势，且只有一个波峰，与泊松分布、正态分布的图形相似，进一步对其进行拟合优度检验，确定数据具体服从的分布.

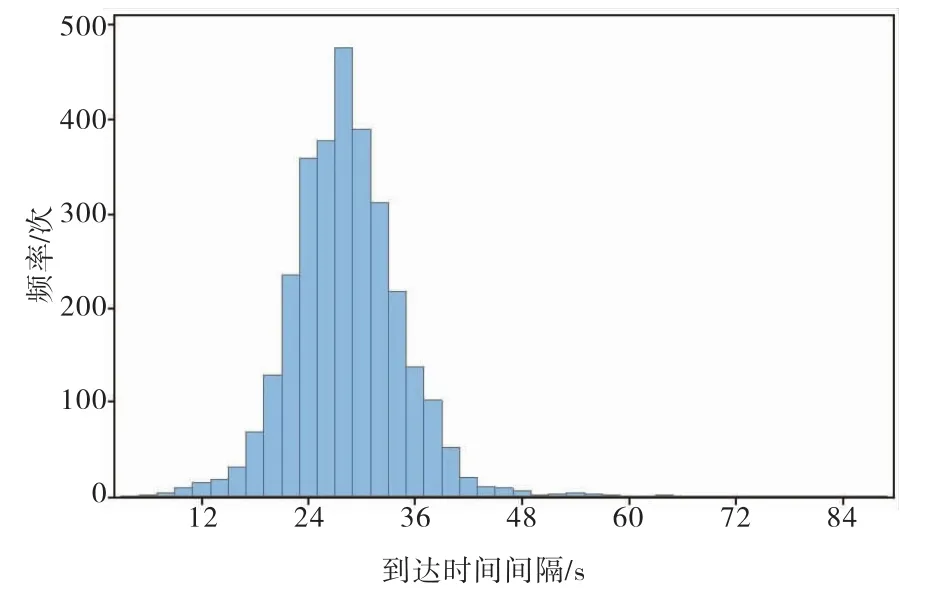
图5 台车到达时间间隔的直方图Fig.5 Histogram of trolley arrival time interval

图6 分货服务时间的直方图Fig.6 Histogram of distribution time

2.4 分布识别

根据直方图已经初步判断出到达时间间隔和服务时间可能服从的分布，对数据进行非参数检验确定数据分布，估计服从分布的参数.检验数据分布的方法主要有Shapiro-Wilk检验、Kolmogrov-Smimov检验、Anderson-Darling检验等，本文选择Kolmogrov-Smimov检验方法对台车到达时间间隔、分货服务时间数据进行分布检验.Kolmogrov-Smimov检验方法是Kolmogrov（1933）提出了检验统计量Dn，并给出了统计量的极限分布［18］：

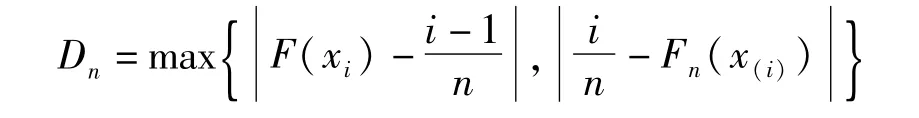
其中：i＝1，2，…，n，Fn（x）表示该组数据的经验分布.

利用SPSS 19.0软件对台车到达时间间隔、分货服务时间，进行Kolmogrov-Smimov检验［19］，检验结果如下：

（1）到达时间间隔

Kolmogorov-Smirnov检验结果如表3所示，结果表明，在显著性水平为0.05时，渐进显著性p＝0.226＞0.05，接受原假设，可以认为台车到达时间间隔的总体分布与泊松分布无显著差异，台车到达的总体分布符合参数为27.79的泊松分布，即认为台车的到达时间间隔1／λ＝27.8 s／辆＝0.46 min／辆，平均到达时间间隔的倒数平均到达率λ＝2.17辆／min.

表3 单样本Kolmogorov－Smirnov检验Tab.3 Single sample Kolmogorov－Smirnov test

（2）服务时间

Kolmogorov-Smirnov检验结果如表4所示.结果表明，在0.05的显著性水平下，渐进显著性p＝0.097＞0.05，故接受原假设，即可以认为分货员服务时间总体分布与正态分布无显著差异.分货服务时间服从均值为301.5，标准差为74.2的正态分布，可以认为分货员的平均服务时间1／μ＝301.5 s／辆＝5.02 min／辆，即平均服务率μ＝0.199辆／min.

表4 单样本Kolmogorov－Smirnov检验Tab.4 Single sample Kolmogorov－Smirnov test

3 优化方案

通过对拍市分货排队系统的观察和分析得到其具有如下特点：1）缓冲区排队的台车是分货员的服务对象，每天拍卖的鲜切花在拍卖开始前台车数和批次数已确定；2）每辆台车拍卖完成后视为进入排队系统，每口大钟等待分货的台车排成一个队列；3）分货员是分货排队系统的服务台，一次分货区每口大钟10名分货员、二次分货区共15名分货员，拍市分货排队系统是由多个分货员并行工作的多服务台系统；4）分货员服务每辆台车的时间是随机的，对台车的服务遵循先到先服务（FCFS）的原则；5）已经求得到达时间间隔服从平均到达率λ＝2.17辆／min的泊松分布；分货服务时间服从平均服务率μ＝0.199辆／min指数分布.综上所述，拍市的拍后分货排队系统实际上是一个有限顾客源的两级单队列多服务台排队系统，如图7所示.

图7 排队系统示意图Fig.7 Schematic diagram of queuing system

3.1 排队系统各项参数指标

统计分货员数量改变时排队系统各项参数指标的变化情况，包括排队系统的服务强度、等待概率、平均队长、排队长、平均等待时间及平均逗留时间，具体数据变化情况见表5.

表5 排队系统一次分货各项参数指标优化前后变化情况Tab.5 Changes before and after optimization of each parameter index of the queuing system

通过对排队系统各项参数指标的统计结果可知，与前文对问题的初步判断相符，当分货员为10人时，服务强度为1.09＞1，等待队列无限长，随着拍卖的不断进行，分货员一直在忙，台车一直在等待的现象普遍存在，直到拍卖结束，没有新的台车进入排队系统，等待队列才开始逐渐缩短，为此需要增加服务台数量来降低服务强度、减少队长.在平均到达率和平均服务率不变的情况下，增加分货员数量，观察各项参数指标的变化情况，分货员增加至11人时，系统中的平均队长约为121辆台车，等待时间约为51 min，台车需要等待的概率仍高达96.69%.由此可见，增加分货员数量能够使平均队长减少，但增加一人并没有明显改善系统的排队状况，继续增加分货员，分货员数量增加至12～15人时，系统中的队长、等待时间、台车到达排队系统后需要等待的概率等各项参数有了明显的改善.

3.2 Flexsim仿真

本文选取K鲜切花拍卖市场某一日的实际供货、交易数据，供货量267.52万枝，共19 265批次，参与购买商669人，利用Flexsim软件对拍市分货排队系统进行仿真.统计该排队系统的仿真分货时间，在模型中添加发生器产生货物表示台车到达；暂存区表示缓冲区、一次分货区、二次分货区；处理器表示分货员对台车进行分货服务；吸收器表示购买商提货台车离开分货区；用A连接对各个实体进行连接，设定各个实体的参数.开始对分货区排队模型进行仿真，一次分货仿真结果见表6.

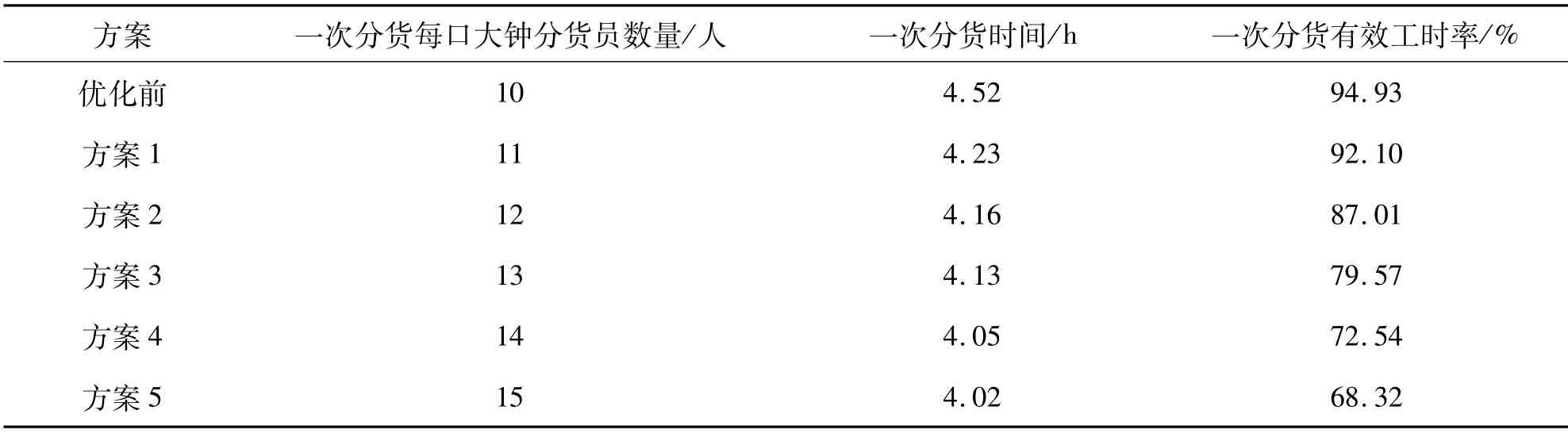
表6 优化前后一次分货结束时间、分货员利用率变化情况Tab.6 Optimize before and after the change of the end time of the first distribution and the utilization rate of the distribution staff

由Flexsim仿真的结果可知，在分货员数量为10人时，分货员利用率为94.93%，分货员处于一个较为忙碌的状态，工作强度大，可能出现分货员超负荷工作的现象.增加分货员的数量，观察仿真结果，分货时间和分货员利用率随着分货员数量的增加逐渐降低.

由前文可知，一次分货效率提高，可以减少二次分货员在分货前段的空闲时间，提高拍后分货环节分货员的利用率，以缩短二次分货的时间，为此在一次分货员每口大钟人数增加后，对二次分货进行仿真，观察一次分货员增加，二次分货员数量不变能否达到提升整体效率的效果.仿真结果见表7.

表7 一次分货员数量增加二次分货时间、分货员利用率变化情况Tab.7 Changes in the time of the second distribution and the utilization rate of the distribution personnel when the number of the first distribution personnel increases

由仿真结果可知，二次分货时间、分货员利用率随着一次分货员数量的增加、分货效率提高（其中二次分货时间包括分货完成后的提货时间），分货员空闲概率降低、分货员利用率不断增加，分货时间有了明显的减少，两次分货环节分货员利用率基本达到平衡.

3.3 排队系统总成本

在考虑排队系统台车等待时间和分货员工作强度的同时，还需要考虑分货作业的成本问题.为了提高分货区的分货效率，本文采用了增加分货员数量的方法，但分货员数量的增加必然导致服务成本的增加；而分货区效率的提高又减少了台车在缓冲区排队等待的时间，降低了排队系统的等待成本.等待成本与服务成本之和为排队系统的总成本，当服务成本的增加值等于或小于等待成本的减少值时，总成本达到一个最佳状态，为此可以通过求总成本的方式最终确定分货员的最优数量.为此建立总成本模型，TC表示总成本，Cs表示服务成本，由一次分货、二次分货及提货的员工薪酬构成，Cw表示等待成本，包括超出购买商等待预期的时间成本.

服务成本Cs取决于工作人员数量、工作时长和平均薪酬.设h1为一次分货时间；h2为二次分货及提货时间；n为一次分货员人数；m为二次分货及提货员数量；η1为一次分货员有效工时率；η2为二次分货及提货员有效工时率；c1为分货员平均时薪.则Cs的计算公式为：

等待成本Cw主要取决于购买商，k为等待超过服务承诺（1 h）购买商数量，h3表示平均等待时间，c2为购买商等待每小时的平均等待成本.则Cw的计算公式为：

据了解，拍市分货员工资是按计件的方式计算的，且两次分货分货员计件工资不同，为此本文调查了两次分货环节分货员的工资情况，计算两次分货分货员每小时薪资的平均值作为总成本中时薪计算依据，分货员时薪c1＝45元／h；据统计，购买商每小时平均等待成本c2＝20元／h，服务成本由两次分货的员工薪酬构成，等待成本为超出购买商预期等待时间，继续雇佣提货人员的时间成本.计算出拍市分货作业每天的分货总成本如表8所示.

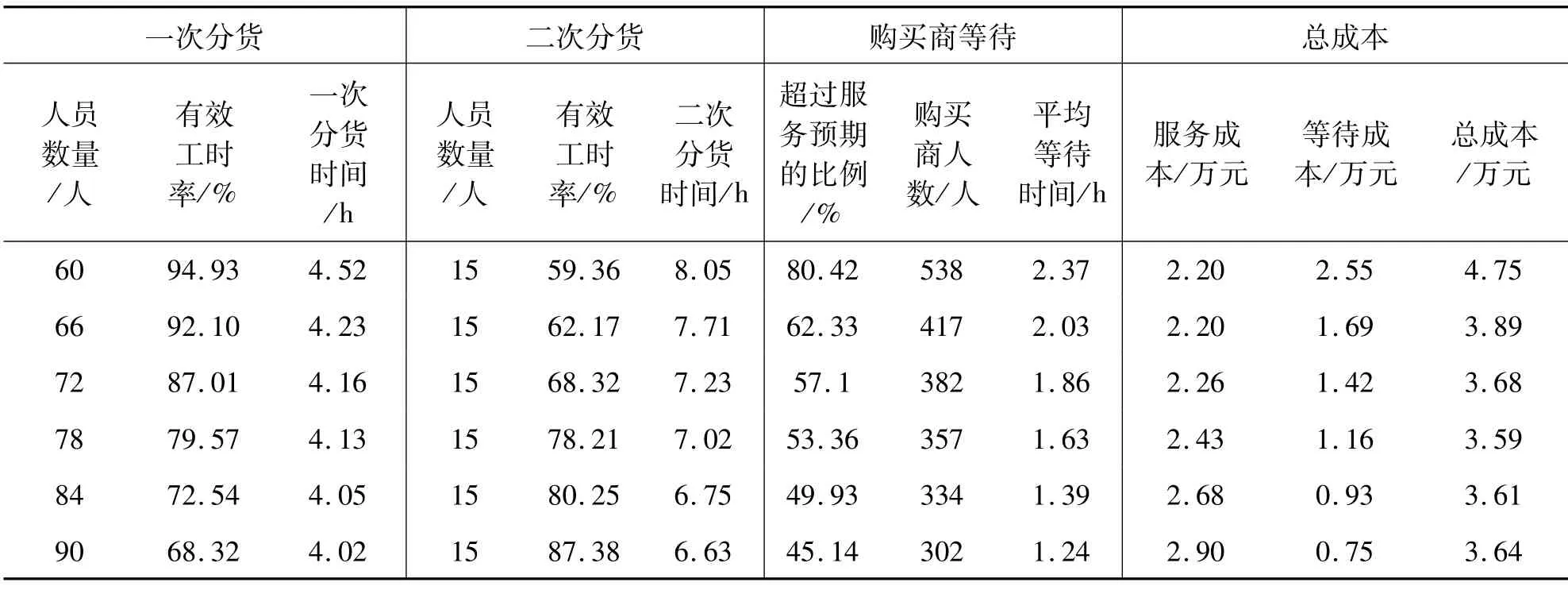
表8 分货总成本变化情况Tab.8 Changes in the total cost of distribution

对比各优化方案的总成本可以看出，分货总成本随着分货员的增加，呈现一个先减后增的趋势，在一次分货员为13人，二次分货员为15人时，总成本达到最低点.

综合上述分析可知，在平均到达率和平均服务率不变的情况下，一次分货员为13人／钟、二次分货员为15人时，两级排队系统的各项参数指标、分货时间、台车等待时间、分货员利用率、分货总成本等都达到了一个较为合适的状态，因此可以确定一次分货每口大钟的分货员为13人，二次分货员为15人时是K鲜切花拍卖市场分货员的最优配置.

4 结论

提升鲜活农产品拍后分货物流效率，对提高整个拍卖市场的服务水平具有重要作用.本文以K鲜切花拍卖市场作为研究对象，拍市的分货物流由两级构成，在具有前后关系的连续排队问题中，要从企业的实际需求出发，以解决企业的实际问题为研究导向，不能将两次排队的流程剥离为两个单独的排队问题进行优化求解.为此本文建立拍卖分货的两级排队系统模型，将分货效率和分货成本作为优化目标，利用Flexsim仿真软件，在数据分析的基础上进行多次仿真实验，根据仿真结果求出不同分货员数量下的分货总成本，得出了分货效率提高而成本降低的拍市分货人员配置的优化方案.该方案在一定程度上可以提高拍市的服务水平，降低分货运营成本，减少购买商因等待提货时间过长而引发的不满情绪，具有一定的理论意义和实用价值，可以为今后类似农产品拍卖市场运营过程中人员配置提供参考.但该工作也存在一些不足之处，没有考虑分货员的劳动强度，而是在分货员的分货效率不会因分货时间的进行而逐渐降低的理想状态下进行仿真、考虑拍市运营成本时没有将顾客投诉损失等因素考虑在内，这将是进一步研究的方向和研究内容.