基于GWO－SVM与随机森林的组合光伏功率预测模型

王 粟，隗磊锋，曾 亮

（湖北工业大学 电气与电子工程学院，湖北 武汉 430068）

0 引言

随着传统能源的不断减少，新能源的开发利用变得尤为重要.其中，太阳能作为丰富的、清洁的能源受到了广泛的关注.然而，光伏输出功率具有间接性、随机性、波动性等特性，随着太阳能发电的不断普及，当大规模的光伏并网时，电力系统的安全运行和电能质量将受到极大影响.因此，准确预测光伏发电功率具有重要的意义［1］.

随着计算机技术和机器学习技术的发展，越来越多的机器学习方法、统计方法以及深度学习方法应用到光伏功率预测.其中包括BP神经网络［2］、支持向量机法（SVM）［3-4］、马尔可夫链［5］、随机森林（RF）［6］、集成算法［7-8］、长短期记忆网络（Long Short-Term Memory，LSTM）［9-10］等.文献［11］提出一种双层BP预测模型，其中，第一层作为功率输出预测，第二层将第一层的输出作为输入拟合实际的功率值；文献［12］通过熵权法将三个单一的预测模型（持续法、支持向量机、相似系数法）组合成一个预测模型，得到预测效果更好的模型；文献［13］采用误差导数法计算两个预测模型（LSTM和Extreme Gradient Boosting，XGBoost）的权重，组合成一个新的模型，由于误差小的模型得到更大的权重，因此整体的误差将减小，预测效果好于单一的预测模型；文献［14］采用EEMD将光伏功率分解为高频、中频、低频三个序列，利用调和平均数法计算三个模型（tree、svm、ensemble）的权重，组成新的模型分别预测三个序列，然后将三个预测值相加得到预测功率；文献［15］提出一种由一个线性模型（双指数平滑法）和两个非线性模型（PSO-BP和ELman）组成的新的预测模型，其中组合权重将使用自适应粒子群优化算法（Daptive Particle Swarm Optimization Algorithm，APSO）进行优化.

采用误差导数法与熵权法的定权组合能够提高单一模型的预测性能，但是当模型的组合方式较为复杂时，单纯的定权组合方式不能够描绘复杂的内部关系.因此，本文采用随机森林算法，对单一模型进行组合，利用随机森林的非线性映射能力，对权重系数进行调节.首先采用灰色关联分析选取相似日，对所选取的相似日分别采用GWO-SVM模型和RF模型进行建模预测；然后采用随机森林，将两个模型的预测结果进行权重分配，得到最终的预测结果.实验结果表明，所提出的组合预测模型的效果要高于单个模型的预测效果.

1 建模原理

1.1 灰色关联分析

假设第i个历史日的气象特征向量为xi＝［xi1，xi2，xi3，xi4］，其中xi1＝［xi1（1），xi1（2），…，xi1（n）］、xi2＝［xi2（1），xi2（2），…，xi2（n）］、xi3＝［xi3（1），xi3（2），…，xi3（n）］和xi4＝［xi4（1），xi4（2），…，xi4（n）］分别表示n个时间点的直射辐照度向量、温度向量、湿度向量和散射辐照度向量；x0＝［x01，x02，x03，x04］表示待预测日的气象特征向量；x0（j）和xi（j）表示预测日与第i个历史日的第j个特征，则x0（j）和xi（j）之间的特征关联系数可表示为：

式中，常数ρ取值为0.5.

因此，预测日x0与历史日xi之间的总关联度可表示为：

1.2 支持向量机

SVM采用结构风险最小化（SRM）原则，最小化由训练误差和置信水平组成的泛化误差上界.在样本数据集较小的情况下也能有效解决非线性问题.

给定训练样本｛xi，yi｝（i＝1，2，…，n），xi和yi分别为输入和输出，通过构造非线性映射φ（x），将样本数据集映射到高维特征空间，构造回归函数：

式中：w为加权向量，b为常数.

求w和b的问题可转化为求取目标函数的极值问题，其表达式为：

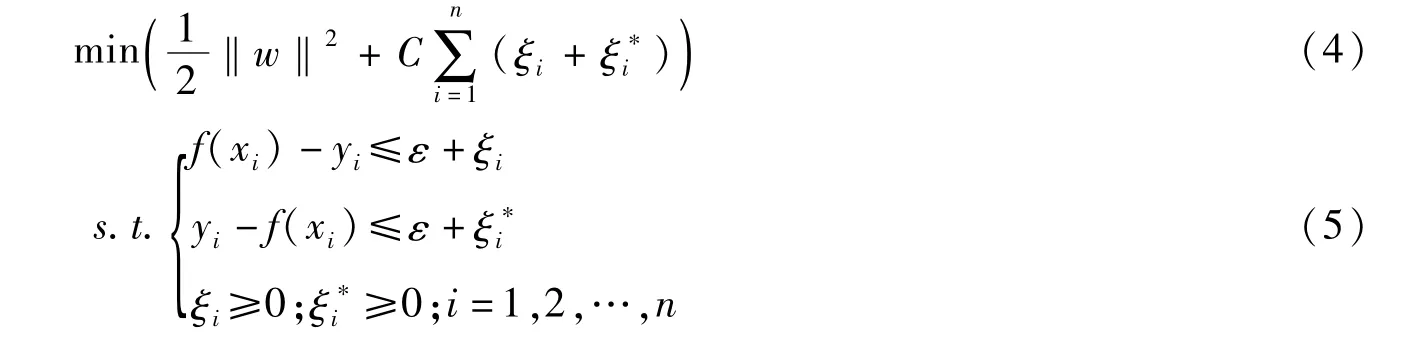
引入拉格朗日乘子αi和，求得SVM回归函数：

本文选取RBF（高斯径向基）核函数作为模型的核函数，其表达式为：

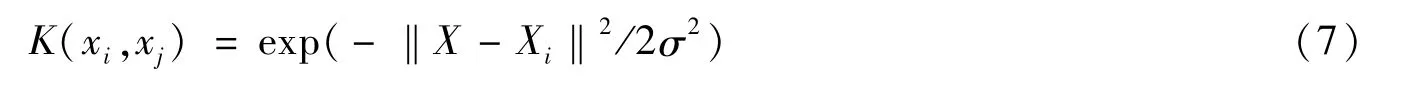
1.3 随机森林算法

随机森林算法是一种基于集成的机器学习算法，由大量的树组成.在随机森林中，通过投票方案提高了一些弱学习者（决策树）的性能.随机森林算法流程如下所示：

1）在N个样本中，通过Bootstrap采样形成T个训练集S1、S2、…、ST.

2）每个训练集S生成对应的决策树C1、C2、…、CT.

4）决策树构建完成后，无需进行剪枝处理.

5）测试集样本X，利用每颗决策树C进行测试，得到预测类别C1（X）、C2（X）、…、CT（X）.

6）所有决策树的平均值作为预测值f（X）：

2 基于GWO－SVM与随机森林的组合模型的功率预测建模

光伏功率的输出会受到直射辐照度、温度、湿度、散射辐照度、风速以及风向等因素的影响.如果将所有的影响因素都作为输入，则会增加模型的复杂性；如果影响因素选择过少，则会降低模型的预测精度.所以，本文选择影响因素较高的直射辐照度、温度、湿度和散射辐照度作为主要的影响因素，对光伏功率进行建模预测.首先，对待预测日进行相似日的选取，在所选取的相似日中，选择相似度最高的前m天作为训练集；然后，将作为GWO-SVM与RF1模型的输入，作为输出对模型进行训练；最后，利用训练好的模型进行预测，得到预测值分别为.其中分别表示每个点的直射辐照度、温度、湿度和散射辐照度，i＝1，2，…，m，j＝1，2，…，n，n为每天功率点的个数；分别为GWO-SVM与RF1模型的预测值；为每个点的功率值.

由于每个模型都有各自的优缺点，能够提供不同的有效信息，因此，预测的效果也会不同.为了提高模型的可信度，可以将多个不同的预测模型进行组合，综合多个模型提供的信息，从而提高预测模型的精度.因此，本文采用随机森林算法，对GWO-SVM和RF1两个单一模型进行组合，利用随机森林的非线性映射能力，对权重系数进行调节.将作为RF2模型的输入，作为RF2模型的输出进行建模训练，利用训练好的组合模型进行预测，得到光伏功率预测值Ppred.基于GWO-SVM与随机森林的组合预测模型如图1所示.

图1 基于GWO－SVM与随机森林的组合预测模型Fig.1 Combination forecasting model based on GWO－SVM and random forest

基于GWO-SVM与随机森林的组合预测模型建模具体步骤为：

1）获取直射辐照度、温度、湿度、散射辐照度等历史值，选择记录时间间隔为10 min的值.

2）通过灰色关联分析选择待预测日的相似日，并在筛选出来的相似日中选择相似度最高的前m天.

3）将选取的m天中的直射辐照度、温度、湿度和散射辐照度值作为模型（GWO-SVM、RF1）的输入，功率作为输出进行训练，得到两个模型的预测值分别为

5）预测结果评价.采用平均绝对误差（MPE）、平均绝对误差百分比（MAPE）和均方根误差（RMSE）衡量系统的预测性能，它们分别定义为：

式中：Pmeas（n）为n时刻光伏功率实测值，Ppred（n）为n时刻光伏功率预测值，N为选取的测试数据个数.

3 仿真算例分析

本文数据选择某电站每天（07：00—18：00）历史数据进行仿真.针对电站数据每5 min记录一次，因此，选择取样间隔为每10 min的数据进行仿真.为了验证所提模型的有效性，选择不同的天气情况对模型进行了测试.通过灰色关联分析选择相似度最高的前10天进行训练.本文选择直射辐照度、温度、湿度以及散射度作为模型的输入，为了消除不同输入数据的量纲和数量级不同会对预测结果产生影响，因此，对输入数据进行归一化处理.

本文选择高斯径向基函数作为SVM模型的核函数，并通过灰狼群算法（Grey Wolf Optimizer，GWO）选择最优的系数c值和γ值.影响随机森林性能的主要是决策树个数（ntree）以及节点分裂属性个数（mtry），决策树个数一般取值为100≤ntree≤1 000，分裂属性个数一般取值为（M为输入属性个数）.为了公平起见，GWO种群规模统一设为20，最大迭代次数设为200.RF1决策树数目设为200，节点分裂属性个数设为2.RF2决策树数目设为200，节点分裂属性个数设为1.本文分别对晴天、多云、雨天以及晴转多云四种天气进行了仿真，如图2为四种天气的仿真图.表1为GWO-SVM、RF以及Combined模型对四种不同天气预测值的RMSE、MAE以及MAPE对比，表2为不同组合方法的误差对比.

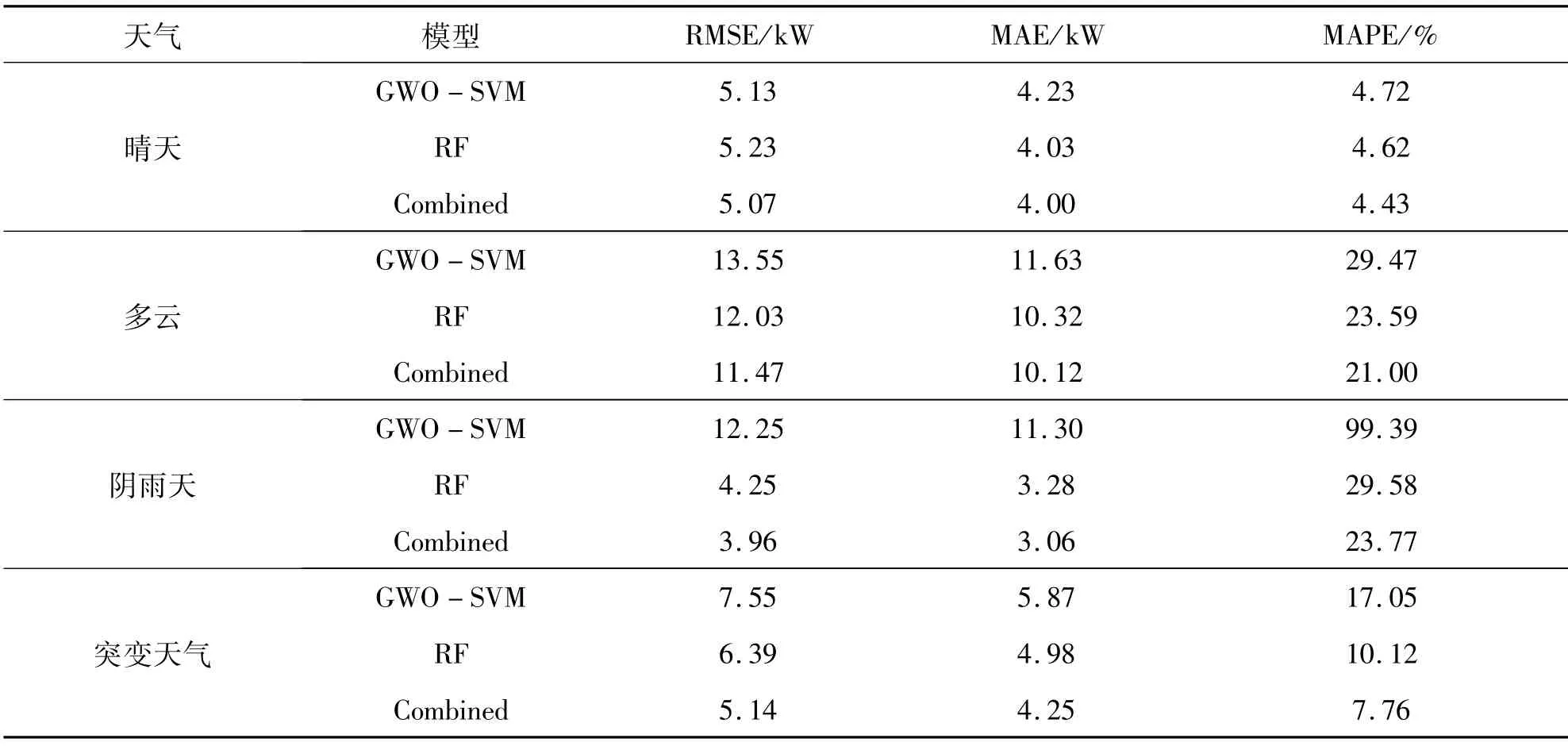
表1 不同模型的预测误差值Tab.1 Forecast error values of different models

表2 不同组合方法的误差对比分析Tab.2 Error comparison analysis of different combination methods

续表2

图2 不同模型预测曲线图Fig.2 Forecast curves of different models

由图2四种天气的预测曲线图、表1和表2对比可以得到：

1）由表1可以得到，对于天气变化较小的晴天，三种预测模型均能得到较好的预测精度；但对于变化频繁且数值变化幅度较大的天气，GWO-SVM预测模型预测效果不如其他两种预测模型.

2）由图2（c）和表1可以得到，在阴雨天时，虽然GWO-SVM模型预测的RMSE和MAE与RF模型和Combined模型相比没有较大差别，但由于原始的功率数值衰减严重，所以GWO-SVM模型的预测精度比另外两种模型低很多.

3）虽然在图2四种天气中，RF模型预测曲线与Combined模型预测曲线极为相近，但从表1可以看出Combined模型预测误差的三种评价指标均好于RF预测模型.

4）对比表1和表2可以看出，采用定权组合（等权法、误差导数法、非等权法）的方法，并非在任何天气情况下都能提高单一模型的预测效果.

5）从表2可以看出，在晴天时，采用等权平均法组合模型的预测精度比本文所提方法高0.45%，但是在阴雨天和突变天气时，本文所提方法均优于等权平均法组合（其中阴雨天预测精度提高了38.11%，突变天气提高了4.84%）.

4 结论

本文提出的灰狼群优化支持向量机和随机森林的组合功率预测模型，将GWO-SVM模型与随机森林模型的预测值作为输入，实际值作为输出进行建模训练，得到预测值.通过仿真可以得到以下结论：

1）光伏功率的输出具有周期性和随机性，特别是天气因素的变化，对功率的输出有很大的影响.

2）由于任何单一的预测模型都有自身局限性，组合模型能够综合单一模型的信息，得到的预测误差评价指标RMSE、MAE、MAPE均优于单一的预测模型.

本文提出的组合预测方法能够减小预测误差，提高预测精度，对于电力调度部门制定发电计划有一定的参考价值，同时提高光伏发电的利用率.但是，提出的灰色关联分析提取相似日，在晴天时的效果较好，在阴雨天相对较差，需要进一步研究相似日的选取方法；同时，组合模型中只选择了两个模型的组合，可以进一步选择多个模型进行组合.