基于PCA和Hausdorff距离的配电网弧光接地故障选线
2021-11-06谢宗禄李富祥李凤强束洪春邓亚琪
钟 健,姚 康,谢宗禄,李富祥,李凤强,束洪春,董 俊,邓亚琪,王 芮
(1.云南电网有限责任公司 临沧供电局,云南 临沧 677000;2.昆明理工大学 电力工程学院,云南 昆明 650500)
0 引言
随着城市配电系统的发展,快速的配电网络故障处置显得尤为重要.在配电网中,单相接地故障率达80%,其中,含弧光的接地故障造成的危害最为严重[1-3],这是因为电弧是动态变化的,会出现燃弧-熄弧的现象[4].在配电系统中,故障产生的电流小,通常可带故障运行1~2小时,但因电弧的存在,使故障电流出现随机性,导致选线算法失败,从而扩大事故影响范围.为及时排除故障,保证系统的安全稳定运行,提高弧光接地故障选线准确率显得尤为重要.
对于配电网的故障选线,国内外已进行了大量的研究.在谐振接地系统中,因电弧不稳定且故障电流小,采用稳态量的群体比幅比相的故障选线方法将会失效[5];利用故障前后馈线零序导纳绝对值之和[6]、互差求和法[7]构造选线判据或形成零序导纳保护[8],但配电网拓扑的变化会引起零序导纳的变化;通过从故障相向系统注入特定频率的方波信号,并分析各馈线零序电流的基波与3次谐波电流幅值比来确定故障线路[9],该方法可排除对地电容的影响,但增加了注入信号的设备;文献[10]对每条馈线上产生的零序电流幅值进行比较并选出故障线路,但馈线较长时,易发生误判;文献[11]根据零序电压导数与零序电流的相关系数实现故障选线,但其易受过渡电阻影响;文献[12]利用谐波中的各特征量作为选线判据,以选出故障馈线,但其易受运行方式的影响,出现误判或漏判现象;文献[13]利用暂态能量法通过定义零序能量函数进行故障选线,但该方法对过渡电阻的适应性较差;文献[14]在S变换提取信号幅频和相频特性基础上选出故障馈线,其选线的可靠性依赖于频率点的模值和相位信息.当接地方式不同时,应适当调整计算数据的选取范围,防止选线算法失效.
PCA具有将数据进行降维处理及特征聚类的特点,加之Hausdorff距离可表征各馈线主成分间的差异性,且不受幅值大小的影响,在弧光接地故障中能准确地辨识出故障线路.结合上述分析,在发生弧光接地故障后,采用主成分分析(principal component analysis,PCA)计算馈线零序电流的主成分个数,再通过Hausdorff距离计算综合关联系数矩阵以识别出故障馈线.
1 单相弧光接地故障暂态特征分析
与研究中常用的稳定接地方式相比,电弧接地故障在实际生活中更为常见,危害较大.弧光接地具有高度非线性与时变的特征,在接地点处会形成电弧,而接地的故障点通过电弧间接接触大地,会产生严重畸变的故障电流以及倍增的过电压,危害较大.电弧特性表示如下:

式中:R1、R2代表不同电弧电流下的电弧电阻值;iarc为电弧电流;Uarc为电弧电压.
电弧接地故障的类型可分为瞬时接地、间歇接地和永久接地,各类型故障时的电弧电压和电流波形如图1所示.在三种故障类型中,瞬时性的弧光接地故障危害最小.若保护装置一直未动作,可能发展为间歇性弧光接地故障或永久性弧光接地故障.因此,针对永久性弧光接地故障时的故障选线显得尤为重要.

图1 常见的弧光接地故障种类Fig.1 Common types of arc ground faults
常用的电弧模型有Cassie模型、Mayer模型、Schwarz模型和控制论模型.Cassie模型适用于大电流燃烧的情况,而Mayer模型、Schwarz模型和控制论模型适用于小电流电弧的特性[15].本文采用控制论模型,其能设置弧长,可直观反映配电线路故障的拉弧情况,表达式为:

式中:g(t)为时间t时电弧动态电导,τc为时间常数,G为电弧稳态电导,Ic为电弧电流峰值,Vc为弧柱稳态场强,rarc为电弧电阻.
2 主成分分析和Hausdorff距离融合的选线判据
2.1 主成分分析
PCA是一种数据降维及特征提取的聚类手段,主要通过降低维度来实现高维度的数据处理,目的是用较少的特征去表征原始数据,将相关性很高的特征转化为相互独立或不相关的特征量.
提取各馈线零序电流作为特征量,应用PCA聚类分析的步骤如下:
1)原始数据标准化:
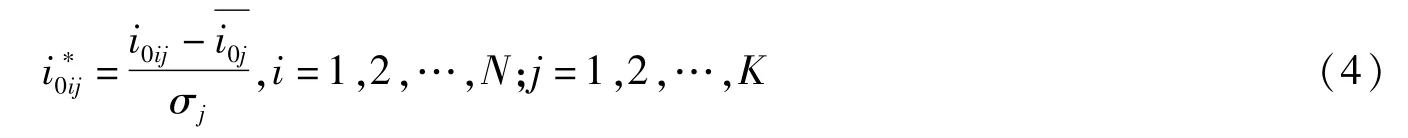
式中:N为馈线条数,K为零序电流的数据长度,i0为馈线零序电流矩阵,i0ij为零序电流矩阵中第i行j列对应的元素为样本第j列的均值,σj为样本的标准差.其中:

2)根据标准化矩阵i*0计算相关系数矩阵R的特征值,并按其大小进行降序排列(λ1≥λ2≥…≥λm),同时得到其对应的特征向量[i1,i2,…,im].
3)确定主成分个数及累计方差贡献率,计算公式如下:
方差贡献率:

累计方差贡献率:

随着主成分个数的增加,其方差呈现出递减的趋势,而其包含的信息量也随之递减.为保证主成分中包含原数据的大量信息,要求累计贡献率达到95%以上.
通过PCA降维后,可在减少输入信息数量的情况下,尽量保留大量的有用信息,提高计算的速度.
2.2 Hausdorff距离
Hausdorff距离[16]表征了集合间的不相似程度.若两个非空有限集合A={a1,a2,…,am},B={b1,b2,…,bn},则两集合间的Hausdorff距离定义为:
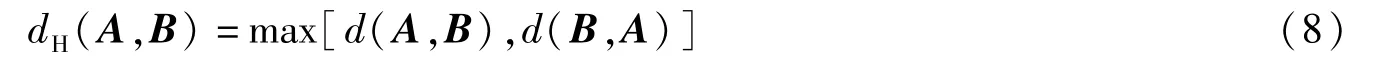
式中,d(A,B)和d(B,A)分别表示为:

式中,‖·‖表示欧氏距离,距离越小,则相似程度越高.因此,本文采用度量曲线间的相似程度,将其定义为:

则其综合关联系数为:

2.3 构造选线判据
根据运行规程,若配电网中性点电压超过相电压的15%,则判断有接地故障发生.现提出采用零序电压变化梯度及其梯度和作为发生接地故障的判据.
零序电压变化梯度:
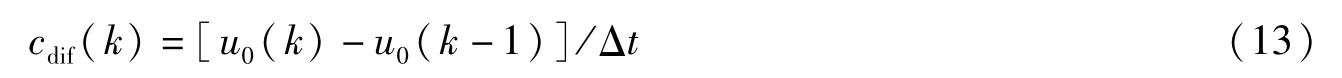
式中:k表示瞬时采样点数;Δt表示采样间隔,ms.
用E(k)表示零序电压梯度和:

式中:K表示一定时窗内的采样点数,k≥K.系统正常运行时,cdif的理论值为零;发生故障之后,E(k)突变明显,可用于装置启动.故障选线的实现步骤如下:
1)当E(k)或u0超过阈值时,判断系统发生接地故障.
2)采集各馈线的暂态零序电流进行主成分分析,通过计算并确定故障累计贡献率达95%的主成分个数.
3)计算各馈线主成分间的Hausdorff距离,得到矩阵H,如式(15)所示:

式中:n表示主成分的个数,对角线上的元素为各主成分间的自相关距离,均为0,余下元素为各主成分间的距离值.
4)利用式(16)和(17)计算出矩阵H的综合关联矩阵H∑:


健全线路间的零序电流波形相似度高,则综合关联矩阵H∑中对应Hj值小;而故障馈线与健全馈线间的零序电流波形相似度低,其综合关联矩阵H∑中对应Hj值较大,选出最大的Hj对应的线路即为故障馈线.具体实施步骤如图2所示.

图2 故障选线流程Fig.2 Flowchart of fault line selection
3 仿真分析
3.1 仿真模型
在PSCAD中搭建含6条馈线的10 kV谐振接地系统,如图3所示.馈线由电缆和架空组成,线路参数分别为:R1=0.17Ω/km,L1=1.20 mH/km,C1=9.70 nF/km;零序阻抗为:R0=0.23Ω/km,L0=5.48 mH/km,C0=6.0 nF/km;电缆馈线的正序阻抗为:R1=0.193Ω/km,L1=0.442 mH/km,C1=143 nF/km;零序阻抗为:R0=1.93Ω/km,L0=5.48 mH/km,C0=143 nF/km.

图3 谐振接地系统图Fig.3 Resonant grounding system diagram
3.2 仿真算例分析
仿真算例1:若距离母线9 km处,馈线L3发生弧光接地故障,过渡电阻为100Ω,故障的初始角为90°.采集各条馈线的零序电流如图4所示.

图4 算例1的各馈线零序电流Fig.4 Zero-sequence current of each feeder in Example 1
对各馈线零序电流进行PCA分析,确定主成分个数,得到各馈线主成分矩阵,如下所示:

各条馈线零序电流主成分间的Hausdorff距离矩阵H为:

则其综合关联系数矩阵为:

由上述矩阵可知,馈线L3零序电流的综合关联系数最大,故判断L3为故障馈线.
仿真算例2:若距离母线6 km处,馈线L4发生弧光接地故障,过渡电阻为50Ω,故障的初始角为90°.采集各条馈线的零序电流如图5所示.

图5 算例2的各馈线零序电流Fig.5 Zero-sequence current of each feeder in Example 2
对各馈线零序电流进行PCA分析,确定主成分个数,得到各馈线主成分矩阵,如下所示:
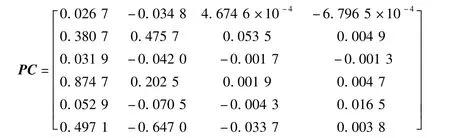
各条馈线零序电流主成分间的Hausdorff距离矩阵H为:

则其综合关联系数矩阵为:

由上述矩阵可知,馈线L3零序电流的综合关联系数最大,故判断L4为故障馈线.
仿真算例3:若距离母线5 km处,馈线L6发生弧光接地故障,过渡电阻为200Ω,故障的初始角为90°.采集各条馈线的零序电流如图6所示.

图6 算例3的各馈线零序电流Fig.6 Zero-sequence current of each feeder in Example 3
对各馈线零序电流进行PCA分析,确定主成分个数,得到各馈线主成分矩阵,如下所示:

各条馈线零序电流主成分间的Hausdorff距离矩阵H为:

则其综合关联系数矩阵为:

由上述矩阵可知,馈线L6零序电流的综合关联系数最大,故判断L6为故障馈线.
3.3 实测数据验证
某变电站发生单相弧光接地故障,选取其实际的录波数据验证本文所提出的选线方法.该变电站有6条馈线,其各馈线零序电流如图7所示.

图7 算例4的各馈线零序电流Fig.7 Zero-sequence current of each feeder in Example 4
对各馈线零序电流进行PCA分析,确定主成分个数,得到各馈线主成分矩阵,如下所示:

各条馈线零序电流主成分间的Hausdorff距离矩阵H为:

则其综合关联系数矩阵为:

由上述矩阵可知,馈线L6零序电流的综合关联系数最大,故判断L6为故障馈线.
4 选线方法的适用性分析
为保证故障选线的准确性,通过改变故障过渡电阻、故障初相角及故障位置等故障工况,以验证该方法的适应性.
4.1 不同故障过渡电阻
若馈线L6发生单相接地故障,故障初相角为90°,将故障过渡电阻分别设置为20Ω、100Ω、200Ω、500Ω,其选线结果如表1所示.

表1 不同故障过渡电阻下的选线结果Tab.1 Fault line selection results under different fault resistances
4.2 不同故障初相角
若馈线L2发生单相接地故障,故障过渡电阻为100Ω,将故障初相角分别设置为5°、30°、60°、90°,其选线结果如表2所示.
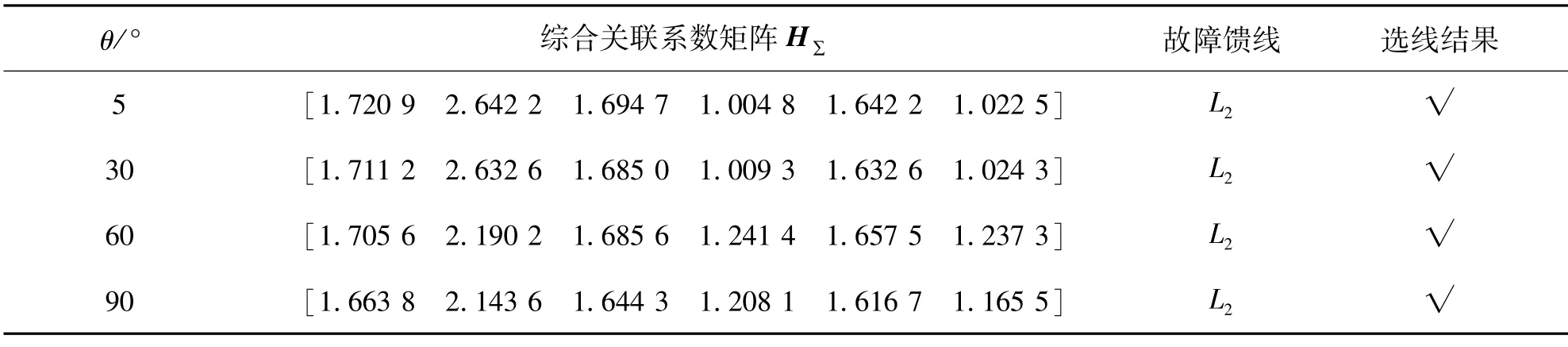
表2 不同故障初相角下的选线结果Tab.2 Fault line selection results under different fault inception angles
4.3 不同故障位置
若馈线L5发生单相接地故障,故障初相角为90°,将故障初相角分别设置为4 km、11 km、17 km、23 km,其选线结果如表3所示.
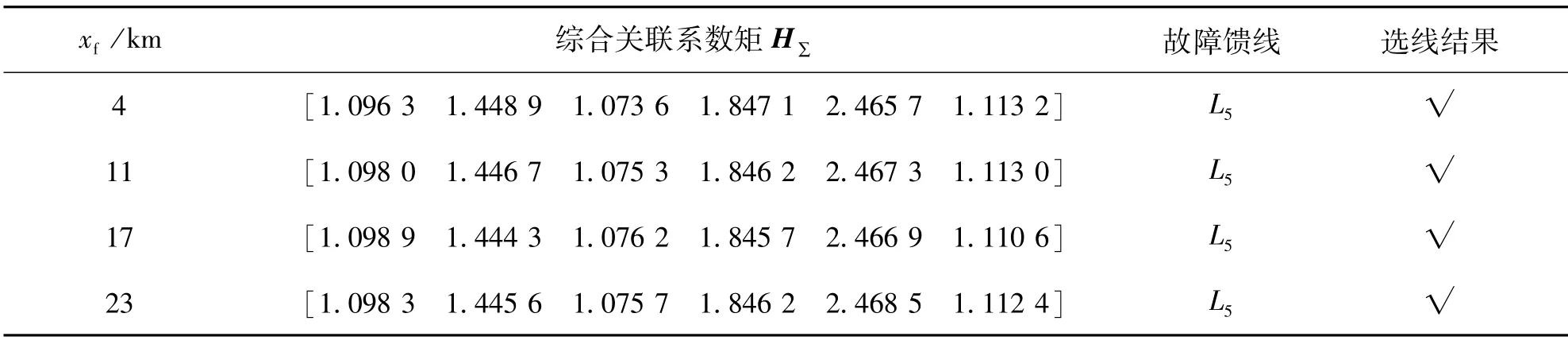
表3 不同故障位置下的选线结果Tab.3 Fault line selection results under different fault locations
5 结论
本文通过采集故障后各馈线的零序电流,进行主成分分析,并结合Hausdorff距离来实现配电网弧光接地的故障选线,并得到如下结论:
1)采用主成分分析各馈线的零序电流,降低了样本数据的维度且抗干扰能力强,提高选线的准确性.
2)运用Hausdorff距离来表征馈线零序电流间的差异性,其不受电流幅值的影响且易于实现.
3)通过仿真分析和现场实测数据,验证所提出的方法能准确可靠地选出故障线路.
