基于分布分数图对一元弱酸相关的滴定曲线的讨论

2021-11-05李娜

大学化学 2021年9期

李娜

北京大学化学与分子工程学院，北京 100871

分布分数图是基于物料平衡原理与解离平衡表达式而绘制的，反映了体系中弱酸碱各相关物种的分布分数(浓度相对值)随pH的变化，在复杂体系的平衡处理中是一个基本且重要的关系式。分布分数在计算溶液pH、不同酸碱型体的浓度、缓冲容量，以及滴定误差等方面均有很好的应用[1–3]。本文基于分布分数对一元弱酸相关的滴定体系之滴定曲线进行讨论，包括一元弱酸的滴定，以及强酸与一元弱酸混合酸的滴定。为不影响讨论主线，本文略去一些基本pH计算以及误差计算过程。

1 一元弱酸的滴定曲线

酸碱滴定曲线是pH–T%函数，其中T%为滴定分数。滴定分数为100% (化学计量点，SP)、99.9%(计量点前0.1%，−0.1% SP)和100.1% (计量点后0.1%，+0.1% SP)是滴定曲线上最重要的三点。滴定分数在从99.9%至100.1%变化时，pH发生突然的改变，称为滴定突跃，pH变化范围称为滴定突跃范围。下面以0.1 mol·L−1NaOH滴定Ka在10−2–10−7之间的同浓度一元弱酸HA为例，对滴定曲线进行讨论。

强碱滴定一元弱酸的滴定分数：

式中：c(NaOH)为滴定剂NaOH的浓度，为0.1 mol·L−1，V(NaOH)为滴定过程中向弱酸溶液中加入0.1 mol·L−1NaOH的体积，ct(HA)为在任意V(NaOH)下，溶液中HA的总浓度，V(HA)为0.1 mol·L−1HA的起始体积。

计量点前，溶液组成为HA-A−，对于计量点前任意滴定分数T%，

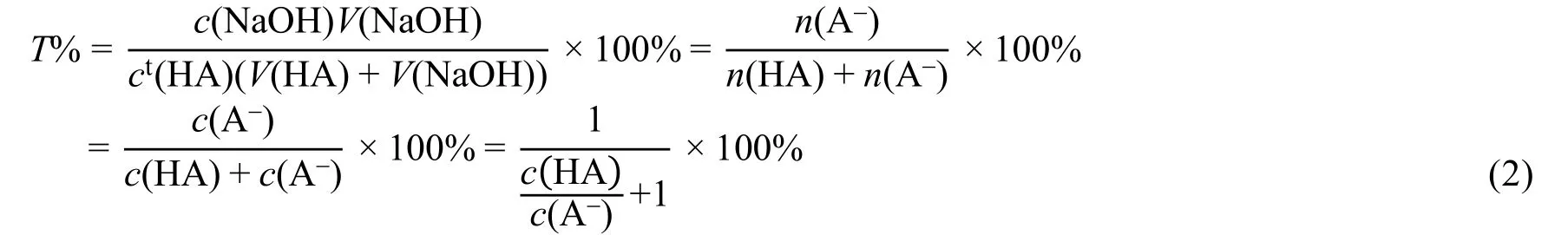
式中：n(HA)与n(A-)分别为HA与A-两种形态的量，c(HA)与c(A-)分别为HA与A-的分析浓度。

对于一元弱酸HA，A-的分布分数为：

由物料平衡式和电荷守恒式可以导出[1,2]：

计算溶液[H+]的公式为：

根据溶液的酸碱性可以选择使用：

或者，

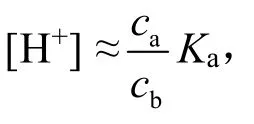
此时，x(A-) × 100%可以表示滴定分数。

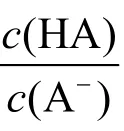
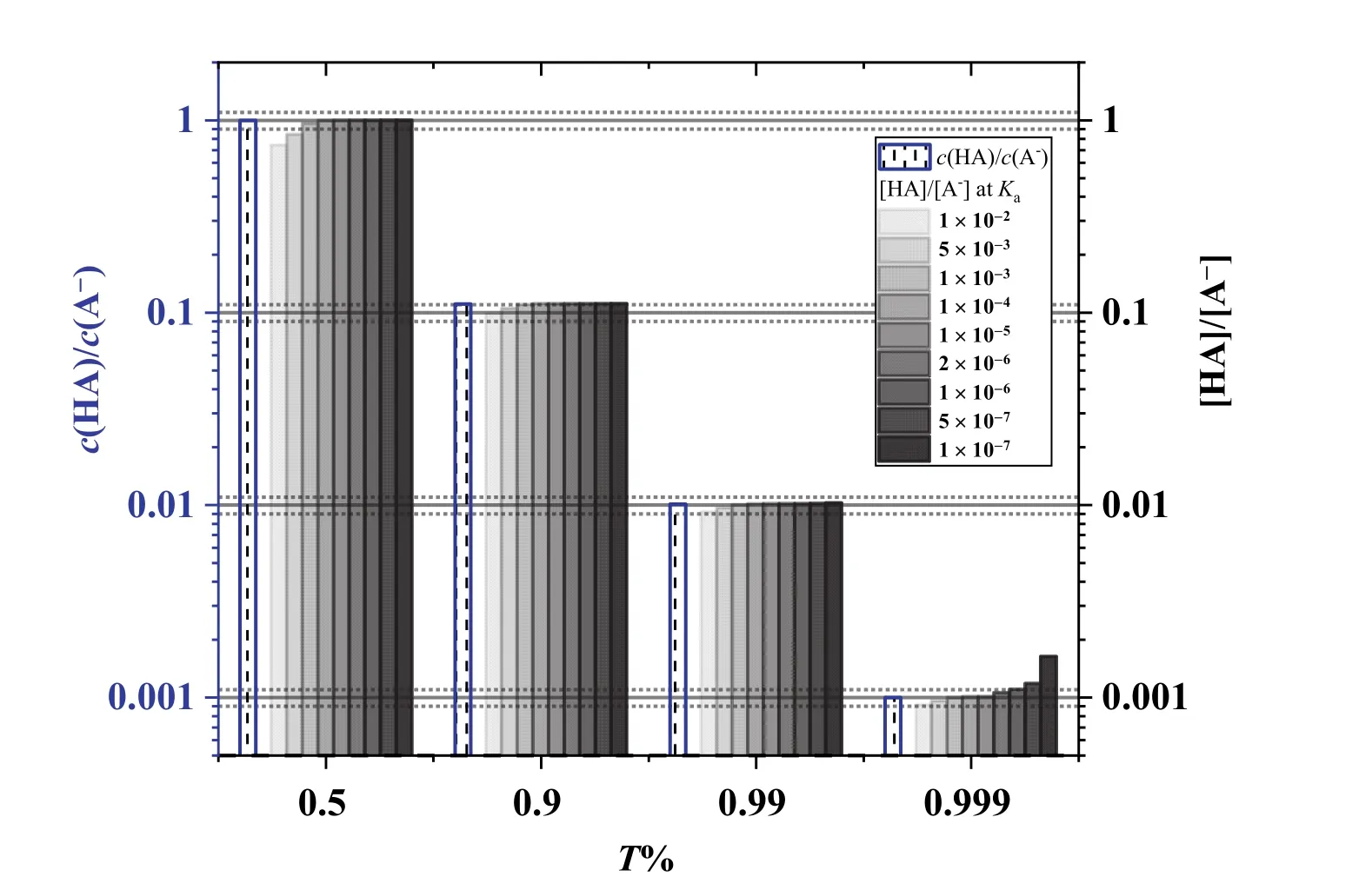
图1 滴定分数为50%，90%，99%，及99.9%时，不同Ka值的HA的以及由近似式求算的

当Ka>2 × 10−6，T% = 100.1%的pH由过量的NaOH计算，pH = 9.7。

因此，以0.1 mol·L−1NaOH滴定Ka≥ 2 × 10−6的同浓度一元弱酸HA，从分布分数图(图2)可以直观地看出来，滴定突跃范围为(pKa+ 3) − 9.7。对于常见的一元弱酸HAc，Ka= 10−4.76，滴定突跃范围为pH 4.76–9.7。滴定突跃范围随着Ka增大而增大，Ka增大10倍，pH (−0.1% SP)向酸性pH扩展1 pH。Ka=2 × 10−6时，滴定突跃范围为8.68–9.74，对应的[H+]浓度与最简式结果相比，误差为～5%，可以近似认为滴定突跃范围为(pKa+ 3) –9.7，即8.7–9.7。

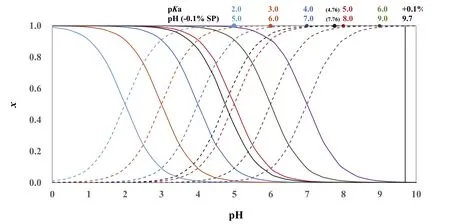
图2 10−2.0，10−3.0，10−4.0，10−4.76，10−5.0，10−6.0和10−7.0的一元弱酸的分布分数图

对于Ka为1 × 10−6的一元弱酸，计量点前0.1%的pH为8.96，对应的[H+]与最简式计算结果相比，误差～9%；计量点后0.1%时，质子条件式中[HA]与c(NaOH)相比不可忽略(c(NaOH) = 0.30[HA])，pH为9.77，与pH = 9.7相比，[H+]的误差约为−15%。对于Ka为1 × 10−7的一元弱酸，同样道理，无法使用最简式从分布分数图获得滴定突跃范围，由近似计算得滴定突跃范围为9.70–10.00；假设可以选到正好在化学计量点的pH变色的指示剂，由于人眼观测滴定终点有±0.3 pH单位的不确定性，终点范围将是9.85 ± 0.3，即9.55–10.15，对应于±0.2%滴定误差；此时若把浓度提高至10倍，即1 mol·L−1，虽然−0.1% SP的pH计算仍不能采用最简式，但是滴定突跃为9.93–10.70，如果选择恰好在化学计量点的pH变色的指示剂，终点范围(10.35 ± 0.3)包含在滴定突跃范围内，滴定误差在±0.1%范围。

下面讨论分布分数对滴定误差的影响。当弱酸的酸性不太强时，只能选择弱碱性范围变色的指示剂，如酚酞(PP)，PP的变色点pH = 9.0。

0.1 mol·L−1NaOH滴定同浓度的HA，根据误差定义，并经合理近似，可得：

式中：下标ep表示滴定终点，sp表示计量点，csp(HA) = 0.05 mol·L−1。

在以PP指示的滴定终点，pHep= 9.0，［OH-］ep= 104× ［H+］ep，［H+］ep与［OH-］ep相比，可被忽略，式(10)简化为：

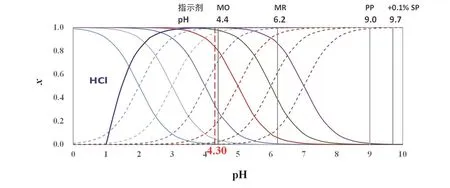
根据式(11)，xep(HA)与E随Ka的变化如表1所示。当HA的酸性较强时，离解度大，xep(HA)较小。当Ka≥ 5 × 10−5时，xep(HA) ≤ 10% × 10-3.7，忽略xep(HA)，误差主要受溶液中的[OH−]ep影响，E= 0.02%；若10% × 10−3.7

表1 0.1 mol·L−1 NaOH滴定同浓度HA的滴定误差(PP指示剂，pHep = 9.0)

2 强酸和一元弱酸混合溶液的滴定曲线

对于强碱滴定强酸和弱酸的混合溶液，以0.1 mol·L-1NaOH滴定同浓度的HCl和HA混合酸溶液(HA的Ka不同)为例进行讨论。HCl滴定分数随pH的变化，以及HA (不同Ka)的分布分数随pH变化如图3所示。

图3 Ka为10−2.0，10−3.0，10−4.0，10−4.76，10−5.0，10−6.0和10−7.0的一元弱酸的分布分数图，及以0.1 mol·L−1 NaOH滴定同浓度的HCl时滴定分数(T% / 10−2)随pH变化

首先，我们来讨论选择性滴定HCl的可能性与条件。

以0.1 mol·L−1NaOH滴定同浓度HCl的突跃范围为pH 4.3–9.7，在−0.1% SP，溶液的pH = 4.30。欲选择滴定强酸和弱酸混合体系中的强酸，终点为弱酸HA体系，须需选择酸性pH范围变色的指示剂。

选择滴定HCl时，根据误差定义，经过合理近似，可得：

使用甲基橙作指示剂时，pHep= 4.4，则式(12)为：

如表2所示，当Ka在10−2.0–10−6.0范围，xepA-≥ 30 × 10-3.1，E主要由xepA-贡献，xepA-> 0.02，即有超过2%的HA参与反应，消耗NaOH，此时无法以不超过±0.1%的误差选择滴定其中的强酸HCl；当Ka= 10−7.0，xep(A-) = 3 × 10-3.1，xep(A−)与10−3.1的贡献不能忽略，此时误差由二者之差决定，误差达到最小值，有0.2%的弱酸被滴定，此时滴定HCl的误差为0.2%。当Ka为10−7.0时，滴定HCl完成后，如前节讨论，可以继续滴定Ka为10−7.0的弱酸。

若以甲基红(MR)为指示剂，滴定终点pH为6.2，即使对于Ka为10−7.0的一元弱酸，也有13.7%的酸参与反应，无法实现选择滴定HCl，也无法实现混合酸总量滴定。

对于Ka≥ 10−7.0的一元弱酸，无法选择滴定HCl，但是可以滴定混合酸总量。原理如前节所述，在此不作详细论述。滴定弱酸，需选择在碱性范围变色的指示剂，如酚酞，pHep= 9.0。

根据滴定总酸量的误差定义，并作合理近似，得：