基于特征点和关键点提取的点云数据压缩方法

李绕波,袁希平,甘 淑,2,毕 瑞,胡 琳

(1.昆明理工大学国土资源工程学院,云南 昆明 650093；2.昆明理工大学 云南省高校高原山区空间信息测绘技术应用工程研究中心,云南 昆明 650093；3.滇西应用技术大学工程学院,云南 大理 671009)

1 引 言

三维激光扫描技术利用激光测距的原理迅速获取扫描对象的三维坐标点云数据,是一种新型的建立物体模型技术。虽然该技术可以快速获取扫描对象的高密度数据,但点云数据的海量特性,为后续存储、处理点云数据带来了很多问题,还直接影响到后续模型重建的精度和效率[1-2]。因此,在保证目标对象模型精度的前提下,有必要对点云数据进行压缩处理,使点云数据量与模型精度相适应。

目前,点云压缩受到了很多学者的重视,并进行了一系列的实验探究,提出了多种压缩方法,在很大程度上改善了点云数据量过大的问题。点云数据压缩应用较为广泛的方法有基于曲率的采样法、基于网格拓扑信息的简化法、基于法矢夹角的简化法等。李金涛等[3]提出基于曲率分级的点云数据压缩方法,该方法对分级后的曲率等级依照一定的准则进行数据压缩,虽然能保留一部分的细节特征点,但在曲率变化缓慢的区域保留的不一点是关键点。贺一波等[4]引入k均值(k-means)聚类方法,首先对点云数据进行分类,通过比较每个点的曲率值和所有点的平均曲率值,实现点云数据的压缩处理。该方法由于不需要建立格网,有一定的速度优势,但点云数据压缩的质量与点云的分类质量和分类组数有关。姚顽强等[5]利用八叉树的树型结构在空间分解上的优势,结合点云的包围盒简化算法,实现点云数据的精简,该算法虽然具有一定的速度优势,但细节特征点保留的较少。李仁忠等[6]对点云建立三维体素栅格,根据估计的法向量,完成对每个三维体素栅格的精简,该方法能实现点云的均匀压缩,但在特征变化较大区域却不能保留较多的特征点。陈西江等[7]提出一种基于法向量夹角信息熵的点云压缩方法,针对不同区域局部熵大小,实现不同程度的点云简化,在特征丰富的区域保留较多的点,信息熵较小的区域保留少部分点。

经过分析上述算法的局限性,本文提出一种基于特征点提取的点云数据压缩方法。该方法首先根据每个点的k邻域估计该点的法向量和曲率值,然后针对曲率值和法向量夹角变化较大的区域提取特征点,在平缓的区域则提取尺度不变特征转换(Scale-invariant feature transform,SIFT)关键点,最后融合特征点和SIFT关键点,并删除重复数据,达到点云精简的目的。该方法既能保留点云的绝大部分特征点,细节信息不易丢失,又能实现冗余数据的去除,最大化的提高了点云数据的质量。

2 压缩方法描述

2.1 基本思路

算法的基本思路如下:1)读取点云,为点云建立拓扑结构；2)计算点云的法向量和曲率；3)提取点云的特征点；4)提取点云的SIFT关键点；5)融合点云数据,删除相同点；6)；保存压缩后的点云。算法流程如图1所示。

图1 算法流程图Fig.1 Algorithm flowchart

2.2 法向量和曲率计算

点云数据的法向量、曲率值等是点云数据的几何属性信息,在特征点提取过程中,为了能较多的保留特征点,需要计算点云的法向量和曲率值。为了快速对点云的邻域搜索,本文采用k-d tree建立点云数据之间的拓扑关系[8],利用k-d tree根据查询点与周围点的欧式距离最小的k个点建立k邻域。

完成所有点的k邻域搜索后,可在此基础上利用主成分分析法(PCA)计算点云的法向量。对于查询点Pi的法向量,近似于估计查询点Pi表面一个相切面的法向量,其k邻域中的点拟合的空间平面方程为:

ax+by+cz-d=0

(1)

式中,a、b、c是平面方程的系数,也是查询点Pi的法向量;x、y、z是k邻域中点的三维坐标值;d是原点到平面的距离。从查询点Pi的k邻域元素创建协方差矩阵A为:

(2)

然后进行k邻域曲面拟合计算查询点Pi的曲率值。二次曲面函数具有普遍的适用性,且便于后续的曲率计算,因此本文采用拟合二次曲面方法计算曲率值,二次曲面的初始拟合函数一般为:

z=f(x,y)=ax2+bxy+cy2+ex+fy

(3)

式中,a、b、c、e和f为二次曲面拟合系数。(3)式是(x,y)的单值函数,一组(x,y)值对应唯一的z值,而采集到的数据中有大量非单值映射的问题[9],因此有必要以查询点Pi为原点建立局部坐标系(μ,υ,ω)。ω轴与Pi处法向量方向一致,μ轴与υ轴相互正交于切平面内,与ω轴共同构成直角坐标系。经过上述一系列的平移与旋转后局部坐标系已建立完成。将(3)式改为局部坐标下的参数表达为:

S(μ,υ)=(μ,υ,ω(μ,υ))

(4)

ω(μ,υ)=aμ2+bμυ+cυ2+eμ+fυ

(5)

式中,a、b、c、e和f为二次曲面拟合参数。由于k邻域的点数一般都大于5,因此依据最小二乘原理,可以求解曲面方程的系数,再根据曲面方程与曲率的关系计算出Pi点的曲率值为:

Hi=a+c

(6)

2.3 特征点提取

2.3.1 边界点提取

对于散乱点云,一般可划分为平坦处点和特征点,而特征点又分为边界点和尖锐点。点云边界点是点云模型几何形状最基础的保证,但在点云数据的压缩过程中,外边界点很容易丢失,导致压缩后的点云模型的边界并不完整,同时也影响到点云的压缩质量,为了避免此问题,本文在压缩过程中先提取点云的边界点,以保证点云模型边界点的完整性。对于散乱点云数据,若Pi点为边界点,则Pi点k邻域中的点则在三维坐标系中会偏向一侧,反之Pi为内部点。利用边界点的这一特性可以根据k邻域的点与查询点Pi构成的法向量夹角的大小识别出边界点,具体实现步骤如下:

(1)查询点Pi为原点建立局部坐标系(μ,υ,ω),该坐标系ω轴与Pi处法向量方向一致,μ轴与υ轴相互正交于切平面内,与ω轴共同构成直角坐标系；

(2)以Pi点为基准点,k邻域中的点Pj为指向点,建立向量vij(j=1,2……k),并将向量投影到上一步建立的局部坐标上形成投影向量vj；

(3)以逆时针为方向,分别计算出两相邻投影向量的夹角βj(j+1)(j=k时,j+1=1),对夹角βj(j+1)升序排序,计算出两相邻夹角的最大差值Lmax；

(4)通过比较给定的角度阈值Lstd与Lmax的大小,判断Pi是否为边界点。若Lmax>Lstd,则Pi为边界点,反之为内部点。

2.3.2 尖锐点提取

尖锐点通常在点云模型的构建中有着至关重要的作用,尖锐点能直接反应点云模型的几何特征。点云的曲率值与相邻法向量之间的夹角值作为点云数据几何形状的刚性特征能直接体现点云模型表面的凹凸性,因此可以将这两个值作为尖锐点识别的重要参数。

(1)在Pi的k邻域中,局部曲率的权值可以根据曲率值进行计算,表达式定义如下:

(7)

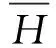
局部曲率权值参数是基于k邻域中的曲率值计算而得,是多个点共同贡献的结果,对单个噪声点并不敏感,因此具有一定的鲁棒性和较强的稳健性。在δi相对较小的地方,说明该区域的几何特征相对较平缓；在δi相对较大的地方,说明该区域曲率值变化较大,点Pi在该区域具有较多的几何信息,成为尖锐点的可能性就越大。

(2)查询点Pi与其k邻域中法向量夹角的平均值可由表达式(8)计算得到:

(8)

式中,αj为点Pi法向量ni与其邻域中点Pj法向量nj的夹角。

(9)

(4)为了避免尖锐检测阈值F难以确定,同时因为尖锐点参数fi受到控制系数λ和τ的共同影响,因此将特征点识别阈值定义为：

式中，Hmax为曲率的最大值;t为所有尖锐点的距离值。若fi>F,则点Pi为尖锐点；反之为平坦处点。

2.4 SIFT关键点提取

点云模型曲率变化缓慢区域的数据压缩通常的做法是进行均匀抽希或统一采样去除邻近点,虽然能实现冗余数据的去除,但这些区域可能也存在一些关键点,容易造成平缓处关键点的丢失,导致压缩效果不尽理想。尺度不变特征转换是一种计算机视觉处理的算法,此算法在1999年由David L所提出并于2004年进行了改善[10-11]。2007年Flint 等[12]人将此算法应用到三维图像数据处理上。该算法基于高斯尺度空间的特征点检测,特征点提取效率高,且可检测的出大量的特征点[13-14],因此本文采用SIFT 算法对曲率变化缓慢的区域进行数据压缩。

二维图像的的方向梯度和角度如下定义[15]:

(10)

式中,Lx和Ly分别使用有限差分来计算:

因此在三维空间中的空间梯度(Lx,L-y,L-t)同样可以计算出,其中:

Lt=L(x,y,t+1)-L(x,y,t-1)

现在将公式(10)扩展到三维空间上,可得到方向梯度和角度

(11)

(12)

下一步需要在给定关键点周围建立加权直方图。利用经线和纬线将θ和φ分成大小相等的柱并创建二维直方图,但从二维扩展到三维由于维度的问题会造成数据偏差,因此在划分的过程中利用方位角将柱归一化处理。方位角的计算公式如下:

=Δφ(cosθ-cos(θ+Δθ))

(13)

添加到直方图中的实际值是较低的且可由公式(14)计算出,直方图的峰值代表了关键点的主方向,可用于创建旋转不变特征。

(14)

式中,(x,y,t)为特征点的位置;(x′,y′,t′)为要添加到方向直方图像素的位置;σ为最小尺度标准偏差。

通过以上步骤,已得到每个关键点的必要信息。接下来为每个关键点建立一个SIFT描述符,使其具有旋转不变性。以关键点为中心,旋转坐标轴使其主方向指向θ=φ=0的方向,旋转矩阵C为:

(15)

最后将关键点的区域划分为4×4的单位小格子,将邻域内的采样点分配到相应的子区域中,并把每个小区域8个方向梯度值累加到直方图中,因此,特征点描述子为4×4×8=128维度的特征向量。

3 实验设计及方法运用对比分析

3.1 实验设计及数据压缩处理

采用3座(1#、2#、3#)雕像作为实验对象。这类点云包含了丰富的特征信息,既有曲率变化缓慢的平坦处点,也有视觉效果特别明显的特征点。首先计算点云的法向量和曲率,其次提取边界线和尖锐点点,然后针对平坦区域提取SIFT关键点,接下来融合边界点、尖锐点和SIFT关键点,并删除相同数据,最后保存压缩结果,完成整个实验。

图2为采用本文算法对3座雕像模型的压缩过程,第一行为第一个雕像的压缩过程,第二行为第二个雕像的压缩过程,第三行为第三个雕像的压缩过程。表1为使用本文算法对3座雕像测试过程中点云数量变化情况。

图2 使用本文算法分别测试3座雕像的过程Fig.2 Using the algorithm of this paper to test the process of three statues separately

表1 使用本文算法测试3座雕像每个过程中点云数量变量情况

在图2(b1)～(b3)中,可以看到点云模型的边界点已被完整的提取出来,保证了(e1)～(e3)边界的完整性。图2(c1)～(c3)是相应的尖锐点提取结果,与原始点云模型相比已提取了模型中绝大数的尖锐点。图2(d1)～(d3)显示提取出的SIFT关键点,虽然已经能呈现了大概的点云的模型,但细节不够完善,因此针对平坦处提取SIFT关键点。表1展示了每个过程点云数量变化情况及最终的压缩率,从表1可知边界点在点云模型中所占的数量最少；由于本文测试的点云模型表面特征较多,因此提取出的尖锐点数量也较多,提取这些尖锐点能保证点云在实现高压缩率的同时点云的几何特征不易丢失。

为了验证本文压缩算法的可靠性,采用文献[3]中基于曲率分级的压缩方法和Geomagic Studio软件中的曲率采样法进行相同压缩率的对比实验分析,1#、2#、3#雕像实验中采用的压缩率分别为:37.00 %、50.40 %和36.40 %。

图3为3种不同的方法压缩3座雕像点云的压缩效果,第一行为第一个雕像不同方法的压缩效果,第二行为第二个雕像不同方法的压缩效果,第三行为第三个雕像不同方法的压缩效果。

图3 3座雕像的原始点云模型与3种压缩方法的压缩效果Fig.3 The original point cloud model of 3 statues and the compression effect of 3 compression methods

3.2 实验视觉效果评价对比分析

由图3可知,三种方法都能达到达到点云压缩的目的,且都能保留一部分的特征点。由于本文的压缩方法是先把特征点提取出来,能对整个点云模型中的特征点做到最大程度的保留,因此在图3(b1)中可以看到1#雕像在压缩后属于特征区域点的颜色较深,而在非特征区(参考图2(c1))的点云数量较少且颜色较浅,整个点云模型的轮廓显示的比较清晰。图5(c1)是基于曲率分级压缩的结果,曲率值越大曲率等级越高,被保留的可能性就越大,所以模型的特征点也能保留一部分,点云模型的轮廓也相对较清晰。由于实验是基于相同的压缩率进行的,图3(c1)在非特征区的颜色比图3(b1)深,说明在非特征区比图3(b1)保留了较多的非特征点,那么特征点保留的数量就会相对的减少,因此会导致点云模型的特征比图3(b1)丢失的较多。图3(d1)是Geomagic studio软件中的曲率采样结果,在点云模型特征变化较大的地方也能够保留一部分特征点,但点云模型的特征相较于图3(b1)已经出现较大的丢失,比如模型中的轮子边缘已相对较模糊,轮子中的几何特征模糊不清,特征点丢失严重。图3(a2)～(d2)与(a3)～(d3)是另外两个模型的压缩对比结果,显示效果与图3(a1)～(d1)基本相同。综上,通过与另外两种基于曲率压缩方法压缩结果的对比,本文所提方法压缩质量更高。

3.3 实验表面积评价对比分析

计算压缩前后点云构建的三角网的面积和,求出总面积变化情况,从而判断压缩前后点云模型特征的变化情况。变化率较大,说明压缩过程中删除了较多的特征点,反之,删除的大部分是冗余数据,对模型的特征改变较小。设第i个三角形(顶点为P1、P2、P3)的面积为Si,则:

(16)

式中,a、b、c分别是ΔP1P2P3三边的边长,p是ΔP1P2P3周长的一半:p=(a+b+c)/2。

对图3中的点云数据进行面积计算,1#雕像压缩前的面积为:26615.77cm2,2#雕像压缩前的面积为:50338.29cm2,3#雕像压缩前的面积为:62130.08cm2。表2列出了面积的变化情况。

表2 3个实验对象应用3种方法压缩后的面积变化情况Tab.2 Changes in area of 3 experimental subjects after applying 3 methods of compression

通过比较分析表2发现,压缩率相同时,在3种压缩方法中本文压缩算法压缩后的点云表面积变化率最小,且数值本身也相对较小,实现了高压缩率而精度损失较小的目的。在压缩过程中并没有删除过多的特征点,点云模型的几何特征保留的较好。

4 结 论

采集到的点云数据中会存在大量的冗余数据,这些数据会降低后续点云模型重建的效率和质量,而现有压缩方法并不能在实现高压缩率的同时,保证压缩后点云模型的精度损失较小。针对此问题,本文提出一种基于特征点和SIFT关键点提取的点云数据压缩方法,该方法在特征区域提取边界点和尖锐点,在平坦处提取SIFT关键点,以确保在特征区或非特征区提取的都是特征点。采用3座雕像的点云数据为实验对象进行分析测试,最终实验结果表明该方法能确保压缩后的点云数据中保留大量的特征点。通过与曲率分级压缩法Geomagic Studio软件中的曲率采样进行对比实验,分析结果同样表明了本文所提方法的可靠性。需要注意的是,在尖锐点的提取过程中,需要设置局部曲率权值控制系数和夹角平均控制系数,由于尖锐点的判断阈值是曲率的最大值,导致这两个系数可选范围较大,为了提高该方法的简洁性,如何自动确定尖锐点提取阈值与局部曲率权值控制系数和夹角平均控制系数将是下一步的研究重点。