突缩突扩式管道能量损失系数影响研究
2021-11-05艾万政
冯 娜,艾万政
(1.银川能源学院,宁夏 银川 750105;2.浙江海洋大学,浙江 舟山 316022)
1 突缩突扩式管道在日常生活中的应用
突缩突扩式管道在日常生活中常被应用于流体测量、管道节流等领域,除此以外,在化学反应混合器、扩散器、喷雾干燥器、燃烧室、电路板散热器等方面也能见到突缩突扩式管道应用的实例。管道内消能工能有效避免外部消能雾化问题,还能达到高效消能的目的,因此,可以将突缩突扩式管道用于管道消能。近年来,随着我国高坝的出现,突扩和突缩流被用于水工泄洪洞消能[1-2]。20世纪60年代,加拿大麦加大坝利用管道水流的突缩和突扩消能原理,在泄洪洞内安装三级洞塞来消能,在大坝使用过程中,三级洞塞的消能效率超过50%,消能效果显著[3]。1988年,中国的小浪底水利枢纽工程考虑到外部消能难以布局,同样采取了在泄洪洞内安装三级孔板,利用水流的突缩和突扩原理来消能的措施。原型观测数据表明,三级孔板总消能率可达到44%,创造了“大流量、高水头”峡谷地区洞内消能的奇迹[4]。由此看来,突缩流在各领域都有广泛的应用,因此,有必要研究突缩突扩式管道能量损失系数的相关流体力学特性,以便于实际工程应用。
2 突缩突扩式管道能量损失系数研究现状
突缩突扩式管道的流态如图1所示。突缩式管道之所以被应用于消能,主要是因为水流在突缩过程中会产生剧烈的剪切和紊动,从而达到消能的目的[5]。尤其是水流突缩后会形成回流区,回流区内水流剧烈旋回和碰撞,是消能的重要源地。
关于突缩式管道液体的能量损失问题,一直是广大专家关注的热点,很多人已从事这方面的研究工作,也取得了大量有价值的成果,其中最著名的代表性成果就是Borda-Carnot公式[1]。该公式描述了液体经过突缩式管道时的能量损失大小与相关要素的关系。Borda-Carnot公式对于层流来说,适用价值较高,但是对于流速较快的紊流而言,其与实际情况偏差较大。主要是因为Borda-Carnot公式在推导过程中假设管道内压力分布均匀,这种简化对于流速不快的层流运动比较适合,但对于紊流来说,突缩流存在分离、漩涡,管道内压力分布复杂,上述假设与实际情况出入较大。Russell等[3]及Fossa等[5]认为,管道突缩流的能量损失大小主要受到突扩或突缩管道的孔径比(d/D)制约(见图1),孔径比越小,管道突缩流的能量损失越大。刘善均等[1]及Wu等[6]在研究孔板水力学特性时认为,当雷诺数大于1.0×105时,对突扩和突缩流的能量损失几乎没有影响。研究突扩和突缩流的专家还有Bullen等[7],他们的研究也局限于突缩突扩式管道的能量损失问题,观点也几乎与Russell、Wu等一致。综上所述,虽然有关突缩突扩式管道的研究较多,但是大多停留在讨论能量损失与相关单个影响因素之间的定性关系层面[8],对于突缩突扩式管道流体力学特性的研究还存在较大的盲区,而且还有很多热点问题有待进一步解决。
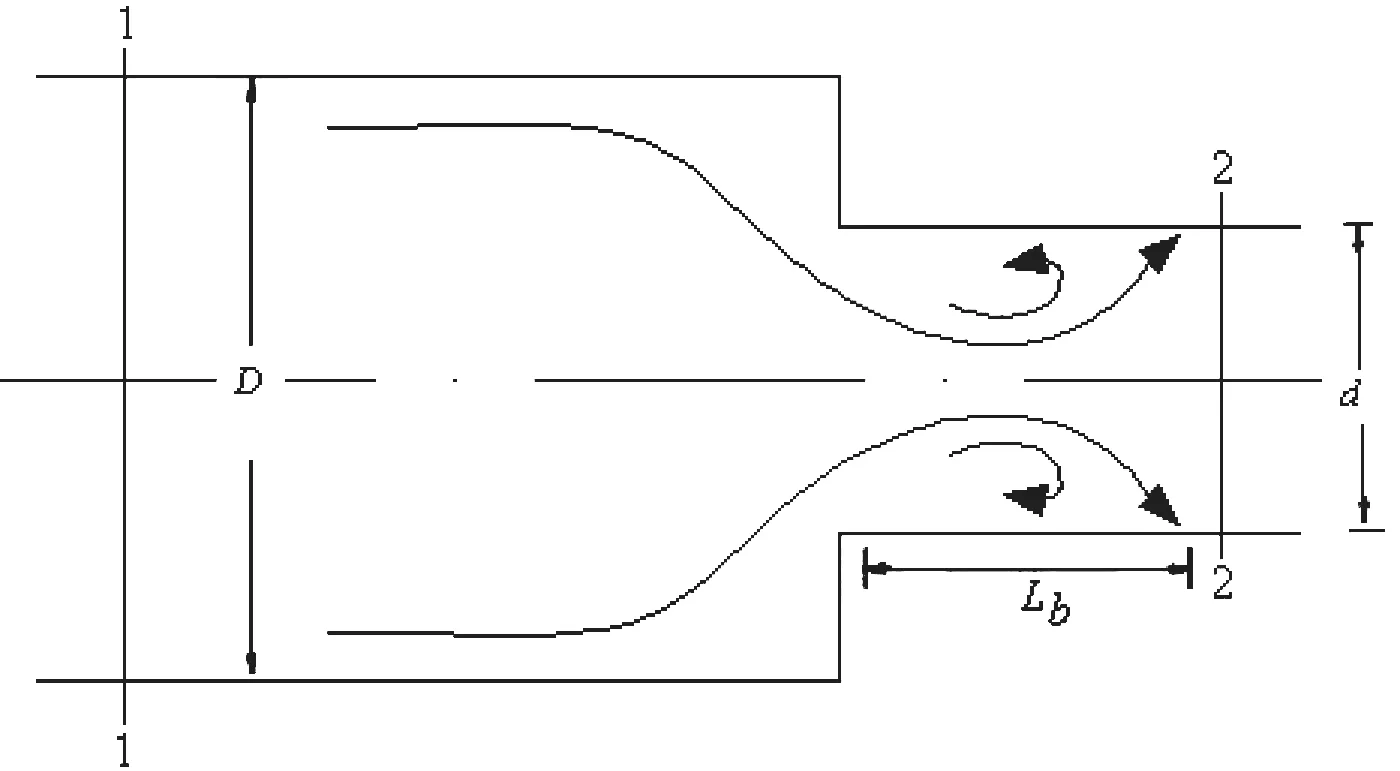
图1 突缩突扩式管道流态
3 能量损失系数定义及影响因素分析
3.1 能量损失系数定义
突缩突扩式管道的能量损失系数是衡量突缩突扩式管道消能能力强弱的重要指标,能量损失系数越大,说明突缩突扩式管道的消能能力越强。
如图1所示,断面1-1位于突缩截面前3.0D(D为突扩管道直径)的位置,断面2-2位于突缩截面后0.5D的位置,d为突缩管道直径,Lb为突缩突扩式管道回流区长度。T为消能工厚度。1-1、2-2断面之间的封闭水体根据能量守恒可得连续方程式(1):

式中:Z1、Z2分别为断面1-1、2-2的高程;P1、P2分别为断面1-1、2-2上的平均压强;α1、α2分别为断面1-1、2-2上的动能修正系数;γw为管道内水的比例;g为重力加速度;v1、v2分别为突缩管道、突扩管道内的平均流速;λ、ξ分别为沿程能量损失系数、局部能量损失系数。
如果突缩突扩式管道水平坡度为0,则Z1=Z2;假设断面1-1、2-2上的平均流速等于突缩突扩式管道内的平均流速,则v=v1=v2;动能修正系数α1、α2几乎相等且均接近于1。由于沿程能量损失系数λ较小,可忽略不计。
通过以上分析,式(1)可简化:

式中:ΔP为断面1-1、2-2之间的压强差。
3.2 能量损失系数影响因素分析
突缩突扩式管道能量损失系数的影响因素有流体特性参数:水流密度ρ、水流动力黏度μ,突缩突扩式管道体型参数:突扩管道直径D、突缩管道直径d、消能工厚度T,流动特性参数:突缩突扩式管道内平均流速v、断面1-1、2-2之间的压强差ΔP、管道回流区长度Lb。影响能量损失系数的参数写成相关表达式:

选取D、v、ρ3个基本物理量,通过无量纲分析法得到无量纲方程:
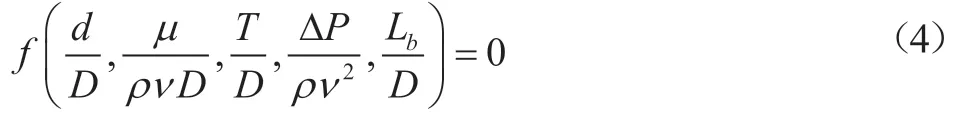
由Red=ρvD/μ,并定义lb=Lb/D,η=d/D,α=T/D,结合式(2)可得ξ,lb=f(η,α,Red)。
影响突缩突扩式管道能量损失系数的因素有孔径比η、雷诺数Re d、厚径比α,并且与回流区长度lb密切相关。
4 数值试验
4.1 数值试验模型
采用的计算模型为RNGk-ε模型,能量损失系数与孔板的孔径比、厚径比、雷诺数密切相关。通过数值模拟,研究雷诺数对能量损失系数的影响以及能量损失系数随孔径比和厚径比的变化关系。数值模型工况一:当突缩突扩式管道的孔径比为0.5,厚径比为0.10,取入口流速分别为0.5、1.0、5.0、10.0和20.0 m/s,对应的雷诺数分别为0.9×105、1.8×105、9.2×105、18.4×105和36.8×105,此时计算在不同流速和雷诺数下的能量损失系数,结果见表1、图2。工况二:入口流速为固定值1.0 m/s,孔径比为0.4、0.5、0.6、0.7和0.8,每种孔径比下的厚径比为0.05、0.10、0.15、0.20和0.25。能量损失系数随孔径比和厚径比的变化关系如表2、图3所示。
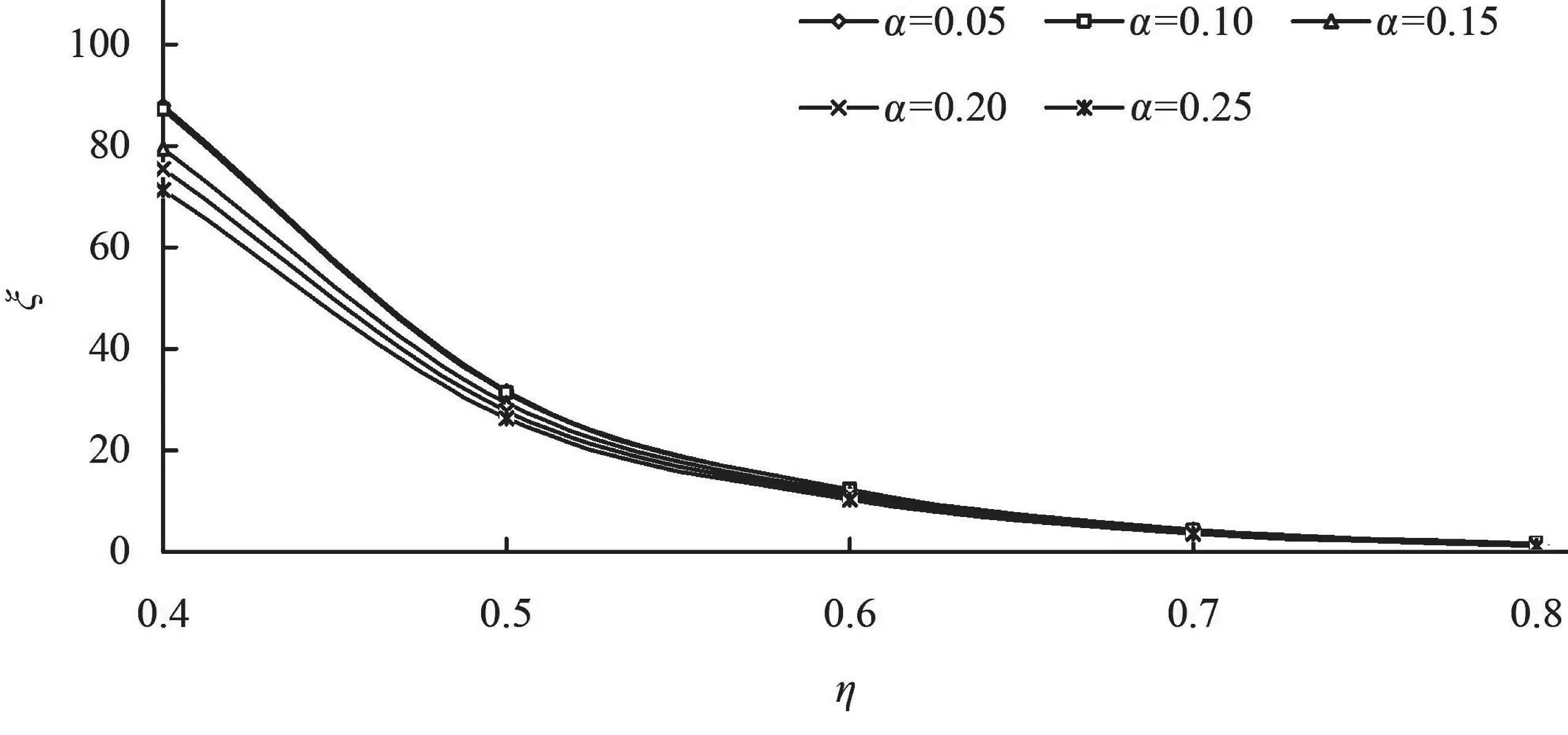
图3 不同厚度下能量损失系数与孔径比之间的关系

表1 不同雷诺数下的能量损失系数

图2 能量损失系数与雷诺数的关系(η=0.5,α=0.10)

表2 雷诺数相同但孔径比和厚径比不同时的能量损失系数
4.2 结果分析
从表1、图2可以看出,当雷诺数小于1.0×105时,能量损失系数随着雷诺数的增大而小幅增大;当雷诺数大于1.0×105时,能量损失系数几乎不随雷诺数的变化而变化。从表2、图3可以看出,在同一厚径比和雷诺数情况下,能量损失系数随着孔径比的增大而逐渐减小;在同一孔径比和雷诺数情况下,能量损失系数随着厚径比的增加而逐渐减小;孔径比对突缩突扩式管道能量损失系数的影响较大,而厚径比对水头损失系数的影响较小;随着孔径比的增大,图3中各条曲线越来越接近,表明随着孔径比的增大,厚径比对能量损失系数的影响逐渐减小。
拟合图3中的曲线,得到忽略雷诺数影响情况下的能量损失系数经验表达式:

式中:η为0.4~0.8,α为0.05~0.25,Red>1.0×105。
5 结语
运用数值模拟的方法,研究了突缩突扩式管道能量损失系数的影响因素。研究结果表明,当雷诺数小于1.0×105时,能量损失系数随着雷诺数的增大而小幅增大;当雷诺数大于1.0×105时,能量损失系数几乎不随雷诺数的变化而变化;在同一厚径比和雷诺数情况下,能量损失系数随着孔径比的增大而逐渐减小;在同一孔径比和雷诺数情况下,能量损失系数随着厚径比的增加而逐渐减小;孔径比对突缩突扩式管道能量损失系数的影响较大,而厚径比对水头损失系数的影响较小。此外,还通过曲线拟合得到了能量损失系数的经验表达式。
