四元二次多项式可约的充要条件

唐善刚,李 伟

(1. 西华师范大学数学与信息学院，四川 南充 637009；2. 安仁中学, 成都 611331)

多项式的因式分解是代数学的一个重要研究内容，但要具体得到多项式的因式分解往往又是困难的，文献［1-10］主要从带余数除法、构造真分数序列与矩阵的初等变换角度给出了一元多项式在剩余类环、有限域，代数体与数域上可约的判定方法及分解因式的若干技巧。文献［11］通过引入张量的概念来研究多元齐次多项式的因式分解，得到了齐次多元多项式基于张量分解下的因式分解的一般方法。文献［12-14］研究了一类特殊的齐3次3元对称多项式的因式分解的技巧及其相关的若干应用。文献［15］系统研究了整系数多元多项式在数学归纳法下逐步转化为多项式环上的一元多项式的因式分解的算法与分解技巧。文献［16-18］将二次实系数多项式在实数域上与复数域上的可约性等价转化为二次型的问题来研究，即二次实系数多项式在复数域上可约等价于二次型的秩不大于2，二次实系数多项式在实数域上可约等价于二次型的秩为1 或秩为2、且符号差为0，根据二次型的线性变换来得到二元多项式的因式分解。文献［19］从矩阵论角度将多元多项式的因式分解与矩阵的MLP分解的算法联系起来，阐述了多元多项式在矩阵MLP 分解下的算法。文献［20］应用多元函数的偏导数与带余除法分析了一些特殊多元多项式的因式分解的技巧。本文讨论二次实系数四元多项式在实数域与复数域上可约的充要条件，得到了仅用二次实系数四元多项式的系数的行列式就能判定其在实数域与复数域上可约的充要条件的新判据，而不用去检验二次型的秩，推广了已有文献的研究结果［16-17］，并统一给出基于实系数对称矩阵的合同变换下的二次实系数四元多项式的因式分解的技巧。

1 基本命题

命题3 整数n ≥1，λi为非0 实数(1 ≤i ≤n)，则关于x1,…,xn的多项式于复数域上可约当且仅当n ≤2。

2 二次四元多项式可约的充要条件

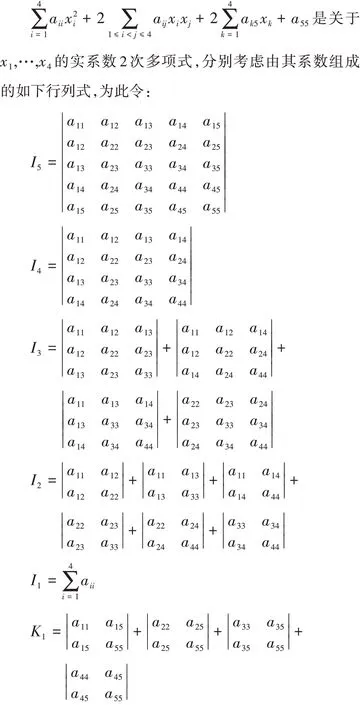
3 应用举例