基于动态自适应变参的粒子群优化算法

李 眩，吴晓兵，童百利

（铜陵职业技术学院经济贸易系，安徽 铜陵 244061）

算法。该算法采用非线性递减策略对惯性权重进行调整,使其具有平衡PSO 算法的全局和局部搜索能力。仝秋娟等［5］、张晓莉等［6］提出一种基于适应度的粒子群优化算法，根据粒子的适应度值动态自适应地调整算法中惯性权重和学习因子的取值，以平衡算法的全局搜索与局部搜索能力，从而避免算法陷入局部极值。杨巍等［7］对基本粒子群算法的更新迭代方式进行了改进，提出一种改进的动态权值自适应粒子群优化算法。采用动态权值自适性优化局部搜索和全局搜索，达到合理搜索的目的。以上研究表明，通过对粒子群算法惯性权重的自适应调整能改善算法的寻优能力。上述基于粒子群算法的惯性权重自适应改进，是改进粒子群算法提升算法效率的一条思路，为后续自适应粒子群算法的研究提供了借鉴。

引 言

粒子群算法（PSO）是模拟鸟群觅食行为发展起来的集群体协作和信息共享的群体智能算法，具有操作简单、收敛速度快、鲁棒性好的特点，且有深刻的智能背景，在科学研究和工程中应用非常广泛。粒子群算法的应用从最初的函数优化扩展到现在的神经网络训练、图像处理、工程领域的过程优化、随机优化问题的求解、最优控制等领域［1］。随着粒子群算法应用研究的深入，传统PSO 算法的局限也相继被发掘，譬如存在早熟收敛或者不收敛、维数灾难、易陷入局部极值等问题［2］。对粒子群算法进行改进可以提高寻优能力。有学者从算法参数的设置来改进算法。李艳等［3］、张娟芝等［4］以PSO算法为基础,提出一种新的自适应调整惯性权重的PSO

由于粒子群算法涉及参数不仅有惯性权重还有加速因子，它们对算法的寻优性能都存在影响。单独调整其中某个参数，忽视其他参数对算法寻优能力的影响，这样的改进存在局限性。基于此，本文尝试运用动态自适应调整策略对传统粒子群算法多个参数进行调整，结合引入自适应变化的控制因子，来改进粒子群算法，以期提高算法执行效率和全局寻优能力。

1 粒子群算法原理

1.1 粒子群算法基本思想

粒子群算法（PSO 算法）起源于对鸟群觅食行为的研究。由于鸟群觅食和优化问题求解在一些方面具有相似性，于是人们模拟鸟群觅食的生物原理进行优化决策和寻找问题最优解［8］。标准PSO 算法实现过程如下：假设在M 维（即有M 个函数自变量）搜索域中，有n 个粒子组成一个群体，n 代表种群规模。种群太小则不能保证粒子群体的多样性，以致算法性能很差，种群太大尽管可以增加寻优的效率，阻止早熟收敛的发生，但无疑会增加计算量，造成收敛时间太长，表现为收敛速度缓慢［9］。Xi=(xi1,xi2,...,xiM)（i = 1,2,...,n），为粒子i的位置向量，粒子维数取决于待优化函数的变量数。 其中，xik∈[ ]

L,U ，代表粒子i在第k 个自变量上的取值。在实际应用中，X 每一维取值保证在一定的范围内，这在函数优化问题中相当于自变量的定义域，L 表示第k 个自变量的取值下限，U 表示第k 个自变量的取值上限。Vi=(vi1,vi2,...,viM)为粒子i 的的速度向量，它们都是M 维的，vik∈[vmin,vmax]，vmin表示粒子在第k 维方向上的最小速度，vmax表示粒子在第k维方向上的最大速度。在每一代寻优中，粒子将根据其自身找到的历史最优位置和群体找到的历史最优位置来调整自己的飞行方向和方位［10］。记Pi=( pi1,pi2,...,piM)为粒子i 自身找到的具有最佳适应值的位置；记Pg=( pg1,pg2,...,pgM)为整个粒子群搜索到的最优位置。

其中，w 为惯性权重，c1与c2为加速因子，r1与r2为随机量。

每一维粒子速度和位置都会被约束在一个范围内，为了防止粒子逃遁出解空间，若超过边界条件，采用如下方法进行处理：

或者

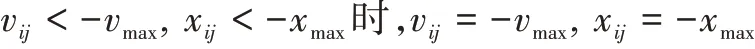
1.2 参数对粒子群算法的影响分析

算法搜索性能对参数有较高的依赖性，算法涉及3个参数：惯性权重w、加速因子c1及c2。3 个参数若设置为定值或者线性变化，则会对算法寻优及效率带来不利影响［11］。3 个参数设置不当可能会使粒子群算法演变成局部寻优算法，或者粒子群在早期就丧失多样性，造成算法早熟收敛［12］。另外，在优化前期，为了粒子具有较大速度，可以提高搜索全局最优解的能力。而在后期接近最优解时，为了不使粒子速度过大而偏离最优位置区域，错失全局最优解而陷入局部最优，因此，在后期接近全局最优区域时，位置更新幅度不宜过大，应该对粒子速度进行有效调整和约束，不能忽视后期粒子可能因速度过大而导致俯冲脱离全局最优区域的情况出现，从而可能造成算法不成熟收敛［13］。鉴于上述原因，在PSO计算中引入非线性变化的收缩因子ρ(t)，与惯性权重相比，其更能有效管束粒子的飞行速度改善算法的收敛能力。

在算法搜索过程中，惯性权重值的变化应该满足如下要求：前期减少的速度比较慢，惯性权重值较大且减少幅度较小利于全局探索；后期较小且减少的速度较快，利于粒子展开精细的局部搜索，这样在保证收敛速度的同时又平衡了全局和局部搜索能力，有效避免陷入局部最优［14］。另外，算法两个加速因子的变化应满足c1先大后小、c2先小后大的要求［15］，这样算法能较好兼顾局部和全局搜索。

2 动态自适应的粒子群算法

随着PSO 算法研究的不断深入，人们考虑到粒子群算法参数对其寻优能力和效率有很大影响，开始关注运用自适应变化的参数提升粒子群算法性能。通常从惯性权重的动态调整入手来优化粒子群算法，较大的惯性权重有利于展开全局搜索，而较小的惯性权重则有利于局部寻优，可以运用惯性权重的自适应调整来协调PSO算法的全局和局部寻优能力［16］。但仅从单一参数的调整来进行优化，其提升算法的性能相对有限，不仅要对算法的惯性权重和加速因子进行动态时变调整，同时引入动态时变的控制因子来约束粒子的位置更新幅度。因为参数值的非线性变化能比线性变化获得更佳的算法性能［17］，李丹提出运用非线性调整的惯性权重来提升算法的探索和开发能力，以获得全局最优的目的。3 项参数的调整皆采取非线性的动态自适应时变调整策略，其随着迭代次数呈非线性变化。惯性权重的动态非线性调整，在此以反正切函数来构建惯性权重调整公式如下：

式中，反正切函数是一个递减的函数，随着自变量的增加，函数值递减的步长逐渐减少。自变量等于1.56 时，函数值等于1，经过反正切函数改进的惯性权重变化正好符合PSO 算法的要求。本文中，wstart=0.9，wend=0.4。当t=1 时，w(t) = wstart= 0.9，当达到最大迭代次数tmax时，w(t) = wend= 0.4。k 为控制因子，控制w 随t 变化曲线的平滑度, k取0.3，算法能取得较好的稳定性。

若仅对w 作出非线性调整会使得算法一旦陷入局部陷阱内就很难跳出，极易收敛到局部极值点。为了改变这种局限性，考虑到加速因子c1，c2对算法全局和局部寻优能力亦有重要影响，因此同时对两个加速因子进行非线性的时变动态调整。以指数函数为基础构造变化关系式，使其分别呈现递减和递增变化，能让算法获得较好的全局寻优性能。其调整函数如下：

其中，c1max，c2max都设为2.0，c1min，c2min都设为0.6，α 为常数，设为0.009。

在前期为了粒子能以较大速度接近最优位置，在后期为了不使粒子速度过大造成俯冲脱离最优位置区域，而错失全局最优解从而陷入局部最优，因此在后期接近全局最优区域时，位置更新幅度不宜过大。对位置更新公式（2）引入动态自适应时变的控制因子ρ(t)，对算法后期粒子位置更新幅度进行约束。其变化规律按照如下函数进行调整：

其中，ρmax设为1.8，ρmin设为0.4，α 为常数，设为0.009。

如此，粒子位置更新公式调整如下：

各参数取值随迭代变化曲线如图1所示。

图1 各参数变化曲线

3 动态自适应PSO算法性能分析

为验证提出的动态自适应变参优化的PSO 算法的性能，用一些典型的复杂函数极值寻优对算法进行测试。第一个测试函数为一个三维函数：

该函数三维图像及其初始粒子分布如图2所示。

图2 f1函数图像及其初始粒子分布图

在测试过程中，取粒子数为100，粒子维数为2 维，最大迭代次数为50 次。为了进一步显示这种改进的有效性，将随机变化权重PSO 算法记为PSO-RIW、惯性权重和加速因子线性动态调整的粒子群算法PSO 算法记为PSO-PIW、非线性动态自适应变参PSO 算法记为PSO-AIW。对迭代过程的适应度函数值变化曲线进行了对比，f1函数3种算法适应度函数值如图3所示。

图3 各PSO算法的适应度值变化

从适应度函数值的变化曲线可以看出，采用带控制收缩的动态自适应变参优化的粒子群算法，在整个寻优过程中自适应度值曲线变化顺畅，能极快跳出局部极值的束缚，快速进入全局收敛，并且收敛时间较短，收敛迭代次数约为5次，表明优化后的算法性能较好。而PSORIW 算法在迭代过程中较易陷入局部极值且不容易跳出，最终没有收敛于全局最优，而且收敛时间长，算法效率不高，全局寻优能力不理想。而PSO-PIW 算法虽收敛于全局最优值，但在迭代过程中陷入局部极值的频次较动态自适应优化的PSO 算法要高，算法性能没后者理想。

第二测试函数是带正弦的三维函数。该函数是一个复杂的多峰多谷函数，存在大量的局部最小值点和高大的障碍物，因为变量之间的关系，优化算法很容易陷入局部最优。f2测试函数关系如下所示：

f2测试函数图像及其初始粒子分布如图4所示。

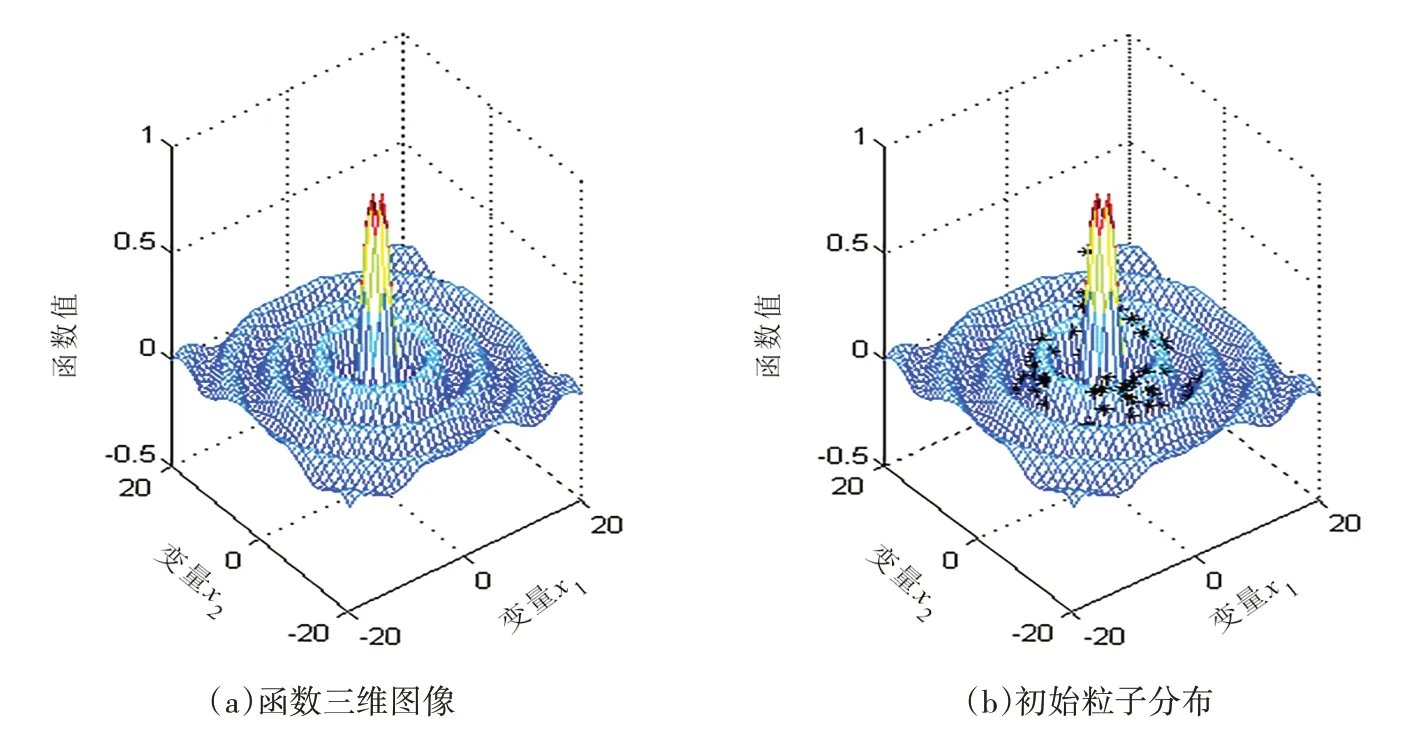
图4 f2函数图像及其初始粒子分布图

为了进一步揭示这种改进的有效性，同样将PSORIW、PSO-PIW、PSO-AIW 算法迭代过程的适应度函数值变化曲线进行了对比，f2函数3 种算法适应度函数值如图5所示：

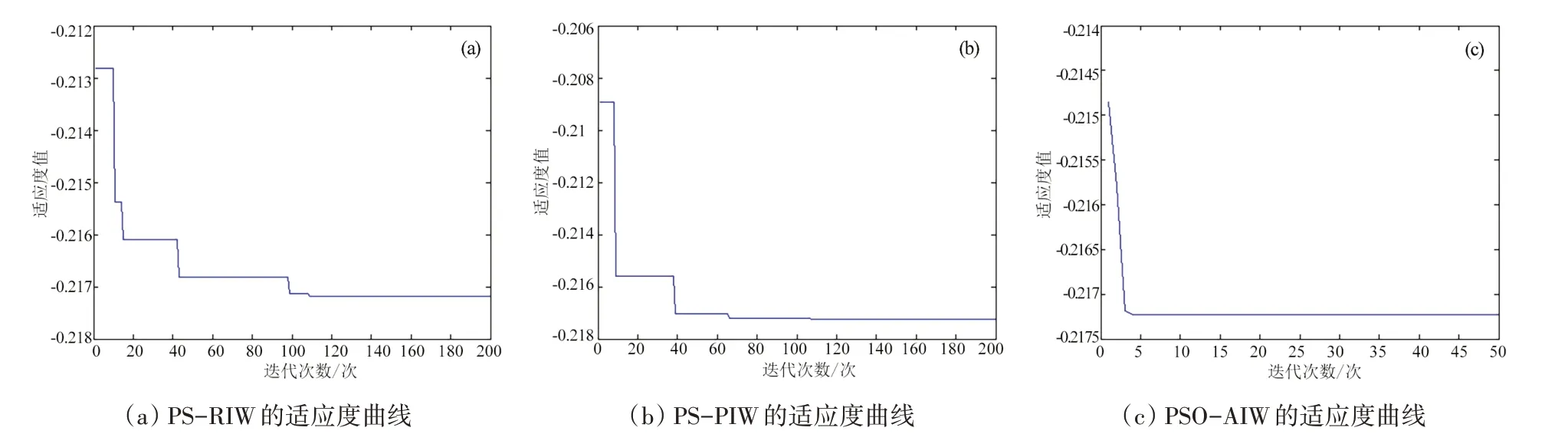
图5 各PSO算法的适应度值变化

从适应度值变化情况来看，PSO-RIW 算法、PSOPIW 算法容易陷入局部极值，寻优收敛时间较长，算法效率较低，且跳出局部最优解的能力较弱。PSO-AIW算法全局收敛的速度极快，没有陷入局部最优，其综合效率是比较高的，同时也说明优化带来的寻优性能的提高还是比较令人满意的。

为进一步探讨改进后的PSO算法在高维情况下的寻优能力和效率，下面用一个高维函数来测试优化粒子群算法性能。采用Sphere函数对其进行测试，其表达式为：

这是一个多维函数，其简单性能有助于探究优化算法在问题多维度上的寻优效果。该函数最优点位于x =(0,0,…,0)，全局最优点的函数值为0［17］。在此自变量取10 维，即该函数取10 个自变量。PSO 算法适应度函数值变化曲线如图6 所示,优化PSO 算法在进化迭代过程中适应度值曲线变化顺畅，表明其在多维函数寻优上也没有陷入局部极值，能快速收敛于全局最优值，说明改进的PSO算法在解决高维优化问题亦有出色的表现。

图6 优化PSO算法适用度值变化

4 结束语

对传统的粒子群算法从惯性权重、加速因子方面进行了动态的自调整优化，并加入动态变化的控制因子来提升算法的效率。结果表明：多个参数的动态自适应调整给粒子群算法带来的性能提升是很显著的，改进后的算法全局寻优能力有了增强。改进的粒子群算法能用于现实当中非线性强、复杂度高的问题（如路径规划、自动化控制等）的求解。粒子群算法改进及其应用具有很大的价值和发展空间。