基于端电压残差的超级电容融合建模方法研究

王 春，陈俑志，马玉婷

（四川轻化工大学a.机械工程学院；b.数学与统计学院，四川 自贡 643000）

引 言

发展新能源汽车是我国从汽车大国迈向汽车强国的必由之路，是应对气候变化、推动绿色发展的战略举措。国务院在《国务院办公厅关于印发新能源汽车产业发展规划（2021—2035 年）的通知》中，将突破整车智能能量管理控制纳入深化“三纵三横”的研发布局中［1］。而超级电容由于其功率密度高、充放电循环寿命长等特点越来越广泛地应用于新能源汽车储能系统［2-5］。

对于新能源汽车而言，超级电容（组）的模型精度直接关系到车辆的安全性、能量决策和使用寿命等［6］。但超级电容由于内部残留电荷和自放电效应的影响，其内部状态会发生不确定变化，并不能轻易得到其真实工作状态［7-8］。因此，为了更好地对超级电容进行状态估计和优化控制，必须建立能够准确反映超级电容工作特性的模型。

目前，常见的超级电容等效电路模型有Rint 模型、Thevenin 模型和GNL 模型等［9-11］。一般地，相较于电池的充放电曲线，超级电容具有更好的线性。因此，众多学者采用形式最为简单，只考虑了欧姆内阻的Rint模型完成超级电容建模。然而，经过实验对比，超级电容还具有一定的极化作用和自放电现象，故能描述极化作用的Thevenin 模型和能描述自放电现象的GNL 模型也常常用于建模过程中［12-15］。但单一模型并不能保证在整个超级电容工作区段内都保持最优精度。换言之，在不同的工作区段，不同的模型有着各自的优势，这表明模型的精度还有进一步提高的可能。

基于此，对上述3 种模型分别进行建模，得到了这3种模型在UDDS（Urban Dynamometer Driving Schedule）工况下的端电压残差情况，并提出融合模型概念。在每一时刻对这3 种模型的优先度进行判断，采用最优的模型作为当前时刻模型。最终模型是由每个时刻的最优模型组合而成，以保证在整个工作区段都能保持最高的精度。

1 超级电容模型解析

超级电容不同于传统化学电源，其储能过程并不会发生化学反应，但由于内部残留电荷、自放电效应和环境等因素的影响，其内部状态会随时间而变化［16］。用等效电路模型代替其真实工作情况虽然会存在一定误差，但其操作相对简单，可行性更高。

以下分别介绍3 种模型（Rint 模型、Thevenin 模型和GNL模型）的电路结构和电路方程［9-11］。

Rint 模型由电源模块和内阻模块两部分组成，其电路结构如图1所示。

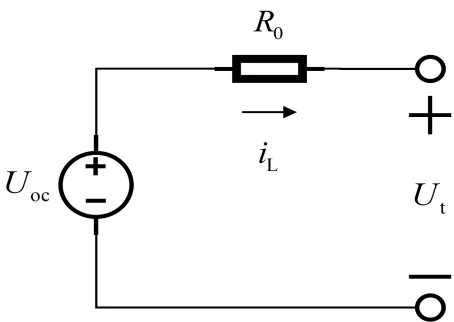
图1 Rint模型

图1 中，Uoc为电源模块；R0为欧姆内阻模块；iL为端电流；Ut为端电压。其数学关系如下：

对式（1）进行离散化处理得式（2）：

式中，Ut,k，Uoc,k，iL,k分别为Ut，Uoc，iL在k 时刻所对应的值，下文中物理量下标k 的用法同样地表示在k 时刻下该物理量所对应的值，下标k+1 表示在k+1 时刻下该物理量所对应的值。

Thevenin 模型是在Rint 模型的基础上串联了一组RC 网络模块，用以描述超级电容的极化特性。由电源模块、内阻模块以及RC 网络模块3 个模块组成，其电路结构如图2所示。

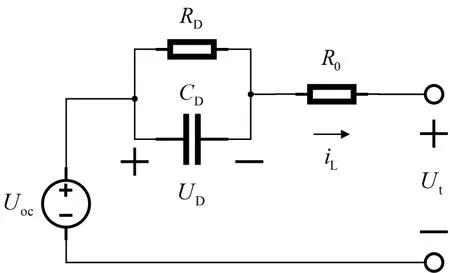
图2 Thevenin模型

图2 中，RD、CD属于RC网络模块,分别为极化内阻和极化电容；UD为RC 网络模块的极化电压。其电路的数学关系式如下：

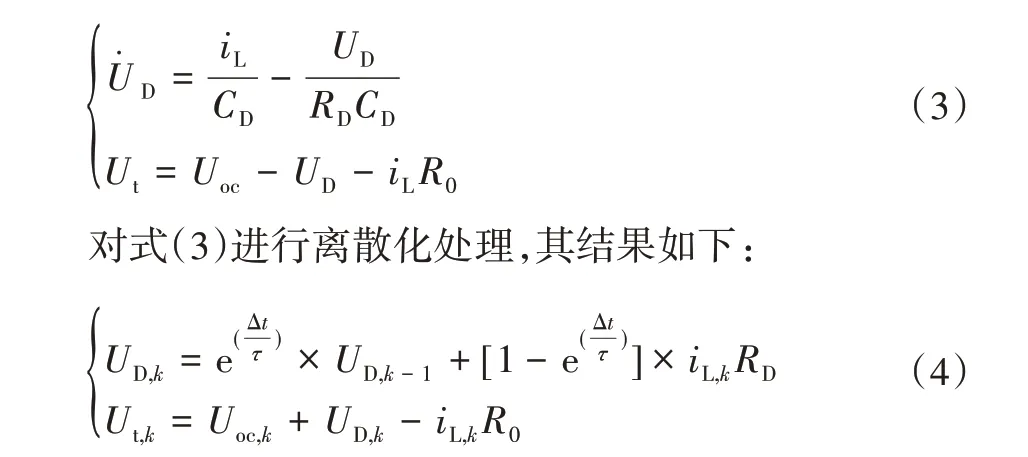
式（4）中，τ为时间常数；Δt为采样时间。

GNL 模型是在Rint模型的基础上串联两组RC 网络模块（一组表示电化学极化，另一组表示浓差极化），同时加入了自放电内阻模块，其电路结构如图3所示。

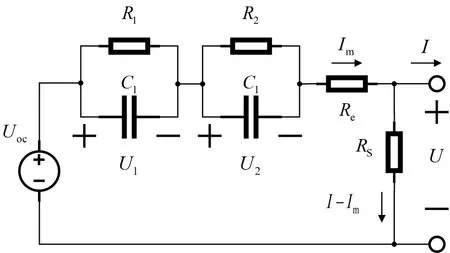
图3 GNL模型

图3 中，R1、R2均表示极化内阻；C1、C2均表示极化电容；U1、U2分别为两组RC 电路的极化电压；Re为支路欧姆内阻；Rs为自放电内阻；I 为干路电流；Im为支路电流；U为自放电内阻电压。该电路的电路方程如下：

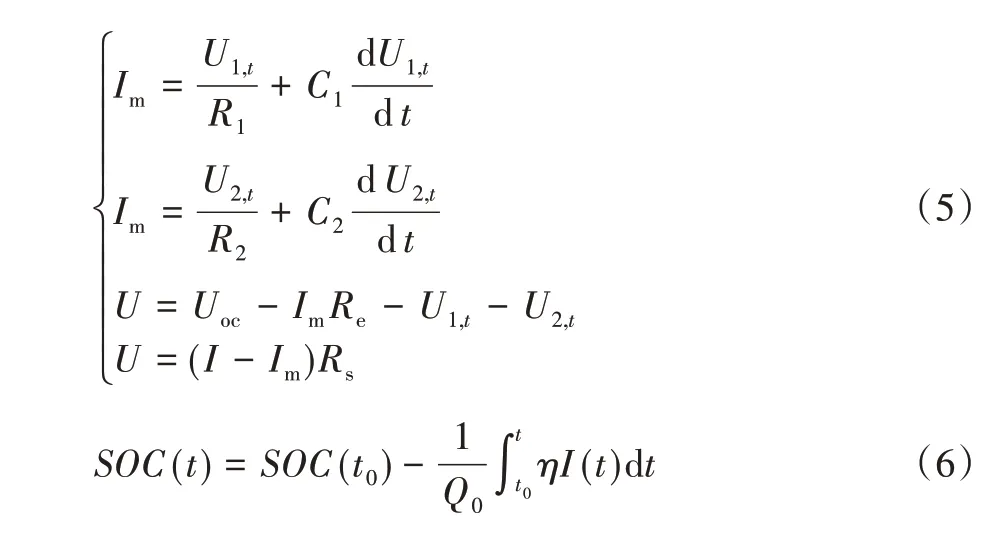
式（5）为GNL模型的数学表达式，式（6）为电流对时间积分所得的t 时刻超级电容荷电状态方程。其中，Q0为电容总容量；η为库伦效率（单次充放电中超级电容放电量与充电量之比），其值默认为1；SOC（State of Charge）为电源荷电状态，其值为当前剩余容量与最大可用容量的比值0~100%；U1,t, U2,t分别为U1, U2在t 时刻下的值。

将式（5）和式（6）进行离散化并整理后，得到状态空间方程如式（7）和式（8）所示：

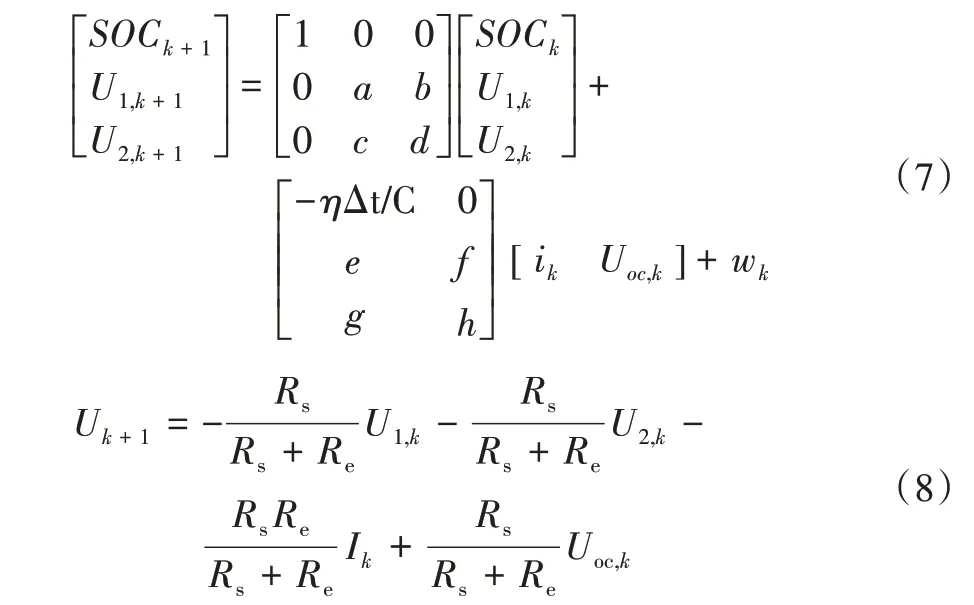
式（7）中，a，b，c，d，e，f，g，h 为模型参数；C 为电路的总电容；wk为系统噪声。

2 基于遗传算法的离线参数辨识

2.1 遗传算法

遗传算法是一种基于生物自然选择的随机搜索算法。与传统搜索算法不同，遗传算法是从随机生成的一组初始解（称为“种群”）开始搜索的［16］。种群的每个个体都是问题的1 个解，个体之间进行选择、交叉、变异得到更优秀的子代并淘汰母代［17］。经过若干代后，算法收敛于最好的子代，它很可能就是问题的最优解或者次优解。其一般步骤如下：

（1）编码，即将初始解（初始种群）进行编码方便后续运算，编码方法可以采用格雷码（Binary Gray Code）、BCD码（Binary-Coded Decimal）等。

（2）选择，即先根据实际问题对初始种群的每个个体进行适应度计算（依照适应度越高该个体越接近真实解的原则，结合实际问题进行求解），然后参照适应度值对母代进行选择（每两个一对，总对数和母代个体数相同，单个个体可以被多次选择，但不能选择同一个个体作为一对），适应度越高，被选择或者重复选择的概率就越高。

（3）交叉，即对选择出的母代个体进行交叉操作，交叉位置由交叉概率随机决定，交叉结束淘汰母代个体，得到还未发生变异的子代。

（4）变异，即最后对交叉产生的个体进行变异操作，得到最终的子代（变异位置随机决定，是否变异由变异概率确定，不是每个个体都一定会变异）。

（5）解码，即得到子代后对子代进行判断，如果不能满足问题要求，则将子代作为新的母代返回上述流程中的（2）“选择”重新进行循环；如果满足要求，则解码最优的1个子代个体作为最终解输出。

2.2 HPPC混合动力脉冲特性测试

HPPC（Hybrid Pulse Power Characteristic）混合动力脉冲特性测试常用于模型参数的离线辨识，采用连续的脉冲激励序列对超级电容进行充放电操作，以获得超级电容在不同SOC 值下的动态特性。超级电容端电压范围设定为0.5 V ～2.7 V，且设定Uoc=0.5 V 时，SOC=0%，Uoc=2.7 V 时，SOC=100%。本次使用的HPPC 测试实验具体流程如下：

（1）超级电容静置180 s 后，以1 A 恒流充电，在电压达到上截止电压2.7 V 后，断开电源静置两小时，此时SOC=100%。

（2）静置结束后，①以1 A 恒流放电5 s，静置10 s，再以1 A 恒流充电5 s，静置10 s；②接着以5 A 恒流放电5 s，静置10 s，再以5 A恒流充电5 s，静置10 s；③最后以10 A 恒流放电5 s，静置10 s，再以10 A 恒流充电5 s，静置10 s；令计数值j= 0。

（3）以1 A 恒流放出额定容量10% 的电量，静置300 s，令j=j+ 1；

（4）如果j< 10，则返回步骤（2），反之则结束循环。循环结束时SOC=0%。

超级电容在混合脉冲测试阶段的电流和电压曲线分别如图4和图5所示。

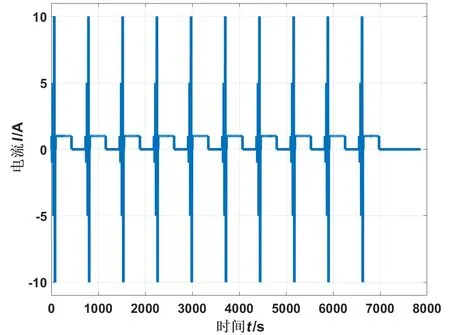
图4 HPPC实验电流图

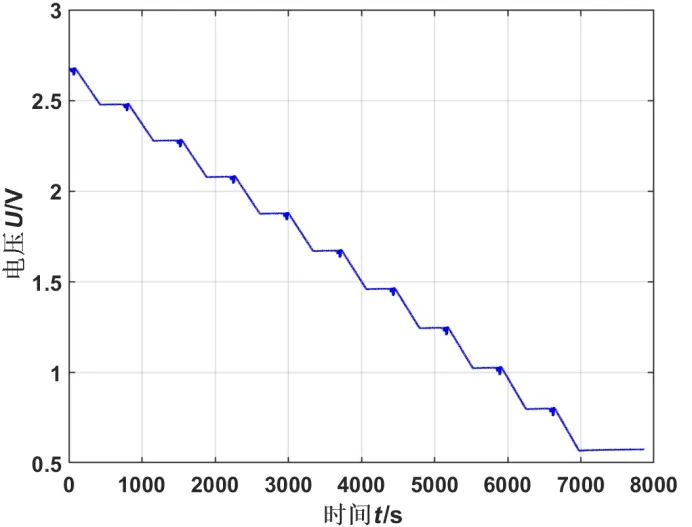
图5 HPPC实验电压图

2.3 离线参数辨识

得到HPPC 测试数据后，通过遗传算法分别对Rint、Thevenin和GNL这3种模型进行离线参数辨识。

离线参数辨识基本流程如下［18-20］：

（1）标定参数辨识区间。基于HPPC充放电曲线，每间隔10%SOC，标定出参数辨识区间，SOC的计算方法如下：

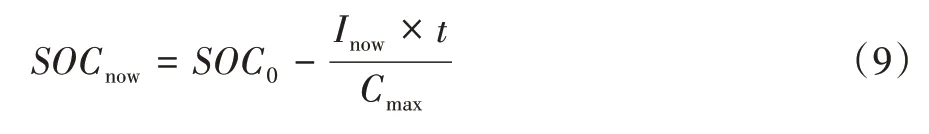
式中，Cmax为超级电容容量（Ah），Inow为当前时刻电流（A），t为时间（s）；SOCnow为当前时刻SOC值，SOC0为初始时刻SOC值。

（2）计算模型中间量Uoc。由于Uoc随SOC保持单调递增关系，因此对式（9）采用多元线性拟合，得到Uoc和SOC之间的关系如下：

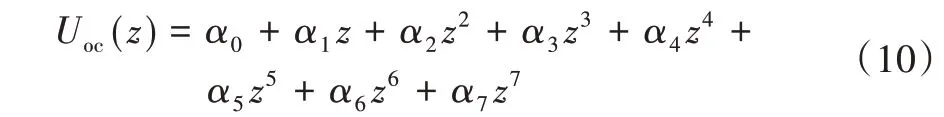
式中，αi（i=0,1,……,7）为拟合系数，z为SOC的值，用于拟合超级电容Uoc和SOC的映射关系。

（3）模型参数初始化。结合模型实际情况，建立两列n行的参数始化矩阵，n等于该模型所需辨识的参数个数，第一列为各参数下限，第二列为各参数上限。

（4）建立适应度函数。将等效模型离散化后的方程代入适应度函数中，该函数以参数矩阵作为输入，以该模型端电压残差作为适应度值返回到遗传算法中。

（5）调用遗传算法工具箱。将参数初始化矩阵和适应度函数代入遗传算法工具箱中，遗传算法工具箱基础参数保持默认即可。

（6）参数验证。将遗传算法返回的参数值代入模型的端电压方程中计算端电压残差值。

若遗传算法求解不理想或者所需代数过多，则可以尝试将参数初始区间减小，或者更换选择、交叉、变异等算子的计算函数，以提升模型精度。

3 基于端电压残差的融合模型

3.1 不同模型下端电压误差比较

通过遗传算法分别对Rint 模型、Thevenin 模型和GNL 模型完成参数辨识，并得到各模型在HPPC 测试数据下的端电压残差数据集。

但由于HPPC 是为参数辨识所设计的实验，与实际工况有着很大的差别，故其端电压残差数据集并不能很好的说明该模型的好坏，需要将不同模型分别代入实际工况数据，得到实际工况下的误差。因此，将3 个模型分别代入UDDS 标准工况实验，得到这3 个模型在UDDS 工况下的端电压误差集（表1）。从表1 中可以看出，3 种模型的最大误差都小于16 mV，平均误差均小于2.5 mV，均方根误差均小于3.2 mV；其中Rint 模型表现最佳，其最大误差比3 个模型中最大值小0.54 mV，平均误差比3 个模型中最大值小0.088 mV，均方根误差比3个模型中最大值小0.099 mV。

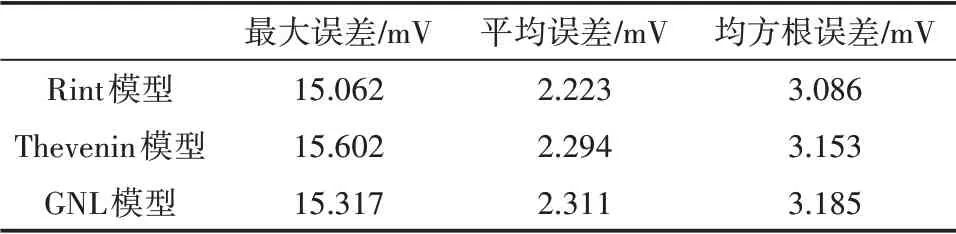
表1 各模型端电压残差对比

然而，虽然采用单一模型的情况下，Rint 模型的整体精度是3 种模型中最高的，但这并不能代表Rint 模型在超级电容的整个工作区段都能保持最佳状态。

为了确定3 个模型在整个工作区段上的优劣性，在每一时刻对3 个模型的误差情况进行对比，选出每一时刻误差最小的模型并进行编号记录，结果如图6所示。

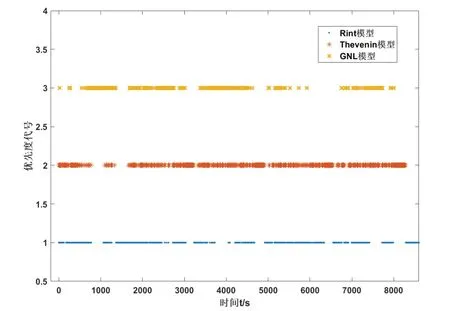
图6 优先度代号图

图6 中，1 代表该时刻Rint 模型优先度最高；2 代表该时刻Thevenin 模型优先度最高；3 代表该时刻GNL 模型优先度最高，每个时刻只有1 个最优模型。图6 中Rint 模型优先的次数为3967 次，占42.41%；Thevenin 模型优先的次数为3689 次，占39.44%；GNL 模型优先的次数为1698次，占18.15%。

结合表1 及图6 可见，Rint 模型并不是在每一时刻都能做到最优，其余两种模型在不同时刻都有着各自的优势区段。这表明模型的精度还有进一步提高的可能。基于此，提出了以这3 种模型为基础的融合模型，即将上述的3 种模型按照其优势区段进行融合以求得到精度更高的模型。

3.2 融合模型的建立

综合上述结论可知，3 个模型之间并没有明显的优势区段分界点，各模型之间的优势区段是相互交错的，通过SOC 区间等特征区域来划分不同模型并不能保证得到的模型为这3 种模型的优势区段的融合。因此，采用基于每一时刻端电压残差切换不同模型的方法进行融合，可以保证整体工作区段都能保持最佳状态。其基本操作流程包括：

（1）模型函数建立。分别建立Rint 模型、Thevenin模型和GNL 模型的残差计算函数，函数输入值为电压、电流值，输出为端电压残差值。

（2）模型优先度判断。其过程如下：①载入UDDS数据，给3个模型设置对应代号；②计算出3个模型方程中需要用到的中间变量；③在每一采样时刻分别将电压、电流数据代入3 个模型的端电压残差计算函数中，得到3 个模型在当前时刻的残差值；④对端电压残差值进行对比，记录下最优模型代号；⑤重复③~④步骤，以得到整个工作区间的最优模型代号。

（3）切换目标函数。载入步骤（2）得到的优先度代号数据，依照优先度代号数据，在每一时刻切换对应代号的模型函数作为当前时刻的模型，即可得到融合模型。

（4）融合模型端电压误差计算。根据当前时刻模型最优代号，将电压电流值代入对应模型的残差计算函数中，并记录下残差值。重复此过程即可得到整个工作区段融合模型的残差情况。

3.3 融合优化模型和未优化模型误差对比

建立融合模型后，将融合模型代入UDDS 工况实验，得到其在真实工况下的误差情况，并与3 种构成融合模型的基础模型进行对比。其对比结果如表2 和图7 所示。

从表2 可以看出，融合模型的最大误差和最小的Rint 模型相同，均为15.062 mV，平均误差为2.070 mV，比3 个基础模型中最小的Rint 模型小6.88%，均方根误差为2.982 mV，比最小的Rint模型小2.69%。

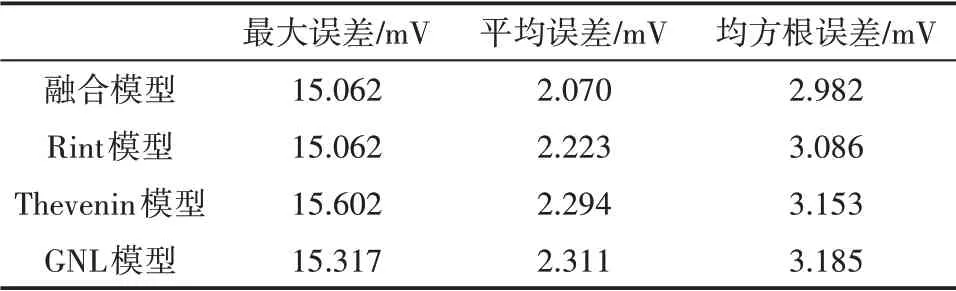
表2 各模型端电压残差对比

图7 所示为各模型端电压残差对比情况。从图中可以看出融合模型的残差曲线的稳定性是高于3 个基础模型的，在1500 s 到2500 s 这个区间上尤为明显。在1900 s到2100 s区间段的放大图中可以发现Thevenin 模型的误差抖动非常明显，Rint模型和GNL 模型的误差抖动略大于融合模型，只有在1950 s 到1980 s 区间，融合模型的抖动大于Rint模型和GNL模型，但总体融合模型的误差抖动都是小于3个基础模型的。

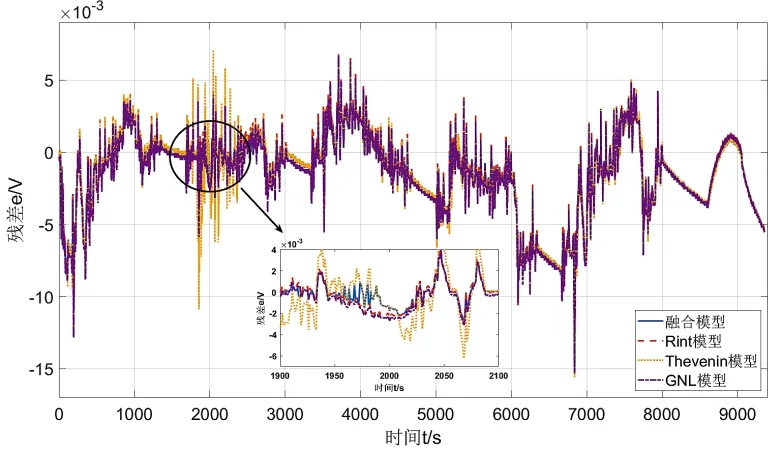
图7 各模型端电压残差对比

结合表2和图7可以发现，相较于单一模型，融合模型有着更高的精度和稳定性，其在整个工作区间段内都能够保持最优的状态。

4 结束语

基于端电压残差将Rint 模型、Thevenin 模型和GNL模型进行融合，得到了精度更高、稳定性更好的融合模型。首先介绍了这3 个电路模型的基本电路结构及其电路方程，然后采用遗传算法通过HPPC 测试数据分别对这3个模型进行了离线参数辨识，并对比了3个模型在UDDS工况下的端电压残差，然后通过每一时刻对超级电容端电压残差值进行判断，选择最优模型的方法得到了融合模型，并且将UDDS数据代入融合模型中，得到了融合模型的端电压残差数据集。与组成融合模型的3个基础模型相比，融合模型在整个工作区段表现是最优的，并且其均方根误差和平均误差分别改善了2.69% 和6.88%。相较于单一模型，这种新的融合建模方法具有更高的精度和可靠性，有利于车载电源的优化控制。