基于影响矩阵法的钢箱拱吊杆索力优化研究

2021-11-05陈秀雯

铁道建筑技术 2021年10期

陈秀雯

（中铁十五局集团第三工程有限公司四川成都 610097）

1 引言

吊杆作为拱桥重要受力构件，其在成桥及运营阶段的受力状态对结构的安全性和耐久性具有重要影响［1］。成桥索力值和目标索力值会存在误差，这是由于吊杆在张拉时会影响其他吊杆的索力，且施工过程不可避免存在人工误差［2］。成桥索力优化是桥梁结构设计的重要组成部分［3］。索力调整涉及到多种参数，索力如果调整不当，会使拱肋、纵梁内力分布不均［4］。合理的索力会使得结构有合适的内力分布，同时也满足了适用性的变形要求［5］。目前索力优化较为常用的方法主要有以下4种：指定受力状态法、索力无约束优化法、索力有约束优化法以及影响矩阵法［6－8］。其中影响矩阵法已由很多工程验证了其在斜拉桥和系杆拱桥成桥后调索的实用性［9］。本文采用影响矩阵法对虞美人大桥钢箱拱吊杆索力进行优化计算。

2 影响矩阵法原理

2.1 施调向量

结构中可以用来实施调整以达到目标值的m个独立元素（吊杆内力调整值）组成的列向量（m≤n，如果m＞n导致未知数大于方程数，出现不定解），记为［10］：

2.2 受调向量

结构中某个力学指标的n个独立元素所组成的列向量（某一时刻吊杆内力值），这些独立元素在调值过程中接受调整以达到某种期望状态，记为：

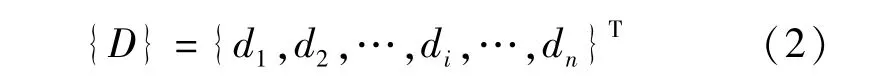
二次调索中的 di（i＝1，2，3，…，n）是吊杆索力需要调整的量，即设计成桥索力向量｛T｝减去调索前的初始索力向量｛T0｝。

2.3 影响向量

当施调向量中某i个元素产生单位变化时导致受调向量的变化，记为：

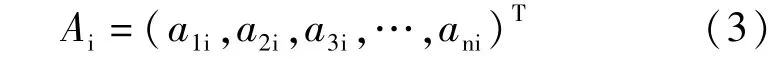
当把所有索发生单位变化产生的影响向量组合起来就是要确定的影响矩阵，记为：

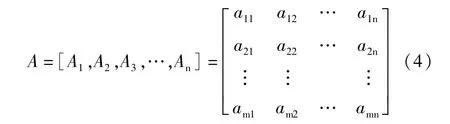
在二次调索过程中，通常认为各索索力之间呈线性关系，即能满足线性叠加原理。基于此认定，建立影响矩阵方程：

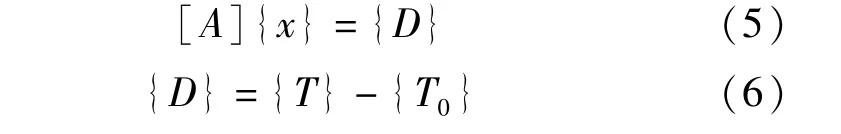
即设计成桥索力向量减去调索前的索力向量。

3 实际应用

3.1 工程概述

虞美人大桥［11］位于安徽省宿州市灵璧县，该桥南北方向跨越新汴河河道。桥梁包括主桥、引桥全长共565 m。主桥部分为装饰钢箱拱夹预应力混凝土连续梁，预应力混凝土连续梁桥承受汽车荷载和人群荷载，装饰钢箱拱则完全独立，仅承受自身重力，边界条件与混凝土桥无交叉。本文中吊杆索力的优化研究不涉及预应力混凝土连续梁桥，仅涉及钢箱系杆拱桥。

装饰钢箱拱桥全长360 m，跨径布置为（80＋200＋80）m，立面布置如图1所示。拱圈为平行双肋钢箱，拱圈的上下边缘线形为2次抛物线，拱脚线形为圆弧＋抛物线组合。主拱圈矢跨比为1∶4.5，净矢高33.7 m，单肋截面宽度为2 m，拱顶拱圈高度为3 m。两片拱圈通过横联连接以增加钢箱拱横向稳定性，中心间距为24.8 m。200 m主跨中有钢箱纵梁直接焊接在主拱圈上作为系梁，钢纵梁高2.2 m，宽1.7 m，整个钢箱拱桥呈彩虹造型。边界上，在中间桥墩上方使用球形支座，拱底处不设置拱脚。

本桥钢箱系杆拱吊杆采用挤压式钢绞线拉索。如图2所示（图中N表示北侧，S表示南侧；后文中W表示西侧，E表示东侧），相邻吊杆在顺桥向的标准中心距为6 m，横桥向采用双侧吊杆，东西两侧中心距为24.8 m。吊索上下端均采用吊耳式，考虑到疲劳、吊装及可更换性，吊索设计安全系数取2.5。现场吊杆布置如图3所示。

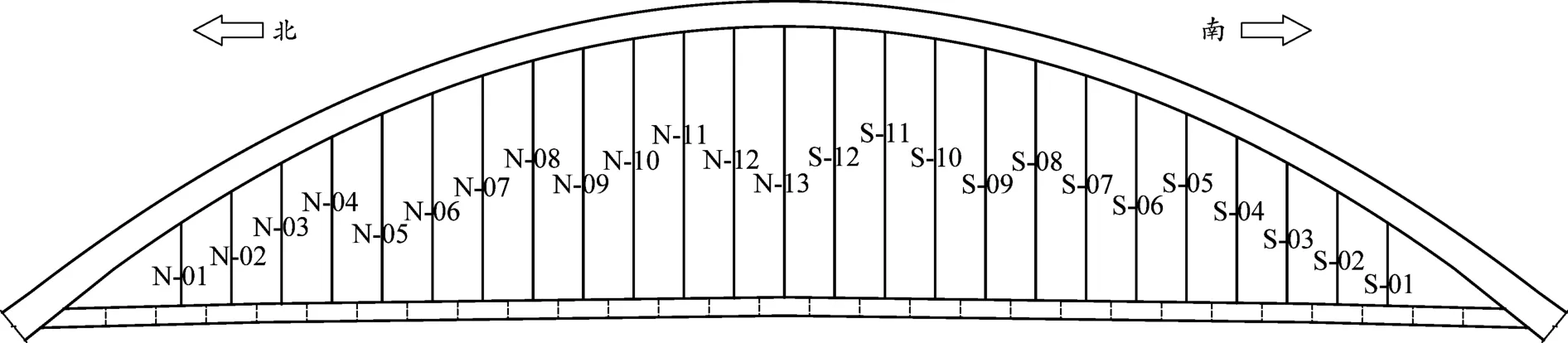
图2 吊杆编号

图3 钢箱拱吊杆布置现场

3.2 有限元模型建立

主跨钢箱拱在中间拱座处其边缘曲线和截面形状沿高度方向渐变，其中拱肋和纵梁之间采用分段焊接，非常复杂。计算模型采用常规的杆系单元等效模拟难以真切表达拱圈刚度。为了充分反映该区段的拱圈刚度，计算中钢箱拱板材直接考虑使用大型有限元软件ANSYS中的Shell181单元进行模拟，吊杆采用Link10只拉单元进行模拟，有限元模型如图4所示。仿真计算过程满足吊杆张拉和体系转换的流程，边界条件符合实际设计要求。

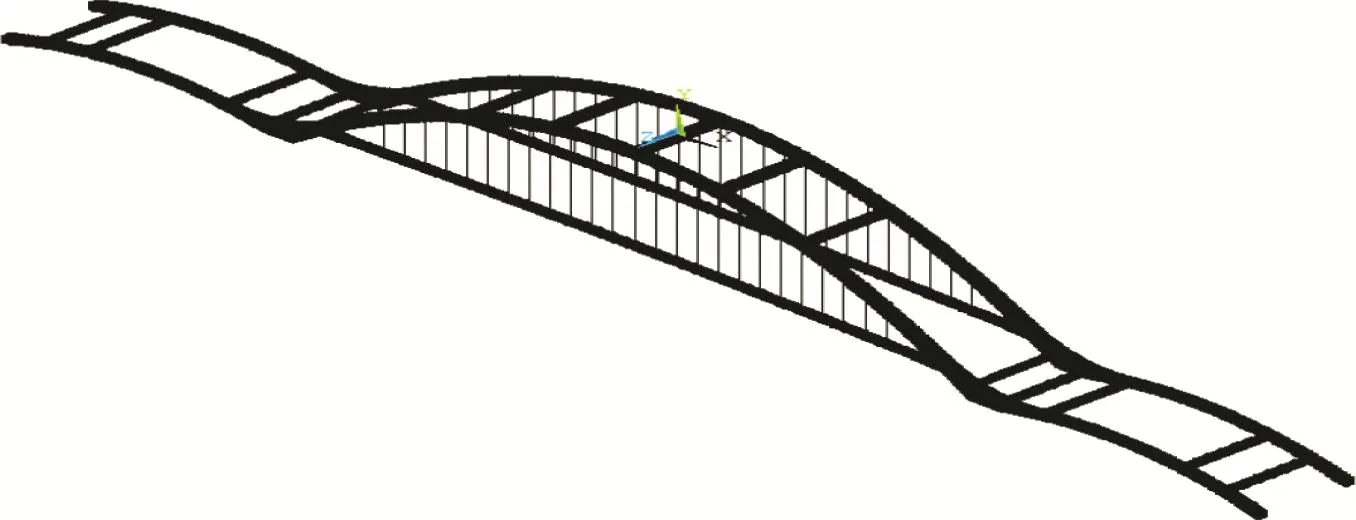
图4 钢箱拱有限元模型

3.3 成桥索力与设计目标索力比较

成桥阶段的索力实际上是根据施工流程最终安装并张拉完成后的索力，并不是理想值。设计的目标索力值恰是理想值。按实际过程将有限元计算结果得到的成桥索力值与吊杆索力的设计值进行对比，如表1所示。显然，两者数值不可能完全相等，有的偏差较大。以目标索力为参照，对成桥进行重新调索，以降低误差。影响向量和影响矩阵是钢箱拱吊杆索力调整中的全局变量集合。单个元素（单根吊杆索力）的数值改变将导致钢箱系杆拱其他吊杆索力变化的值可以通过有限元软件计算获得，并归纳到对应的影响向量和影响矩阵之中。

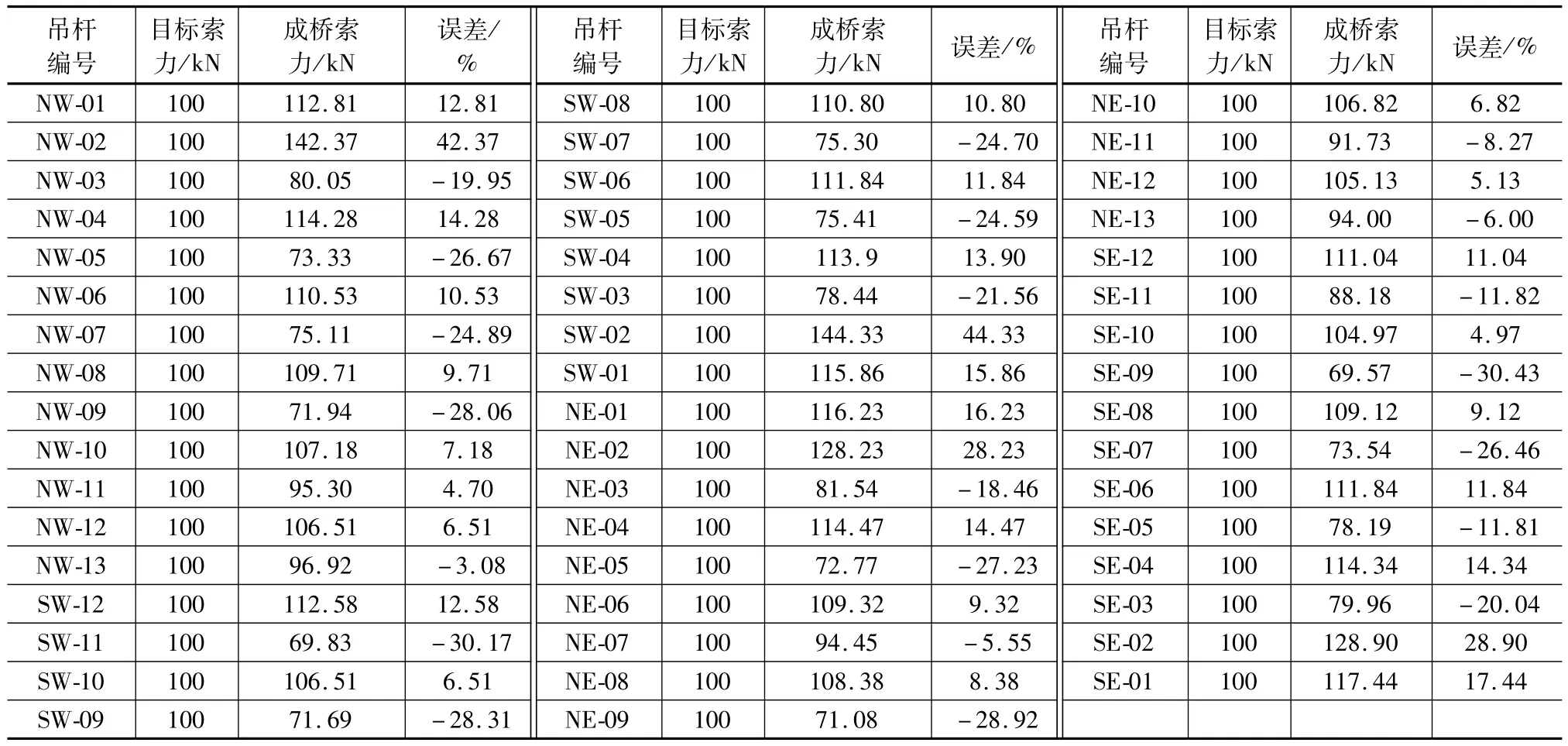
表1 成桥阶段吊杆索力与目标索力比较

4 基于影响矩阵法的二次调索

4.1 影响矩阵求解

影响矩阵［A］可由计算有限元模型得出，向量｛T｝是需要求解的量。影响矩阵［A］的提取过程如下：在模型中依次对每一根吊杆在原有的基础上多张拉10 kN，为了避免影响矩阵出现奇异矩阵，在对每根吊杆张拉10 kN的同时，对其他吊杆张拉0.1 kN，既能避免出现奇异矩阵又可满足迭代精度要求［12］，最后记为矩阵［A］的形式。因篇幅有限，本文只列举50阶矩阵［A］中的部分数据。

4.2 二次调索

在本文计算模型中，可以将吊杆的二次调整值作为变量，并用向量｛T｝＝｛T1，T2，…T50｝来表达。

基于影响矩阵法理论，将设计索力记为向量｛P｝，调整之前的索力向量记为｛P0｝，施调的索力向量记为前述的｛T｝，即：

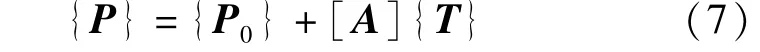
优化模型中，根据表1数据可以确定索力向量｛P｝和｛P0｝。向量｛P｝和｛P0｝以及影响矩阵［A］中的元素应根据张拉顺序进行对应调整。在实际施工过程中，吊杆实际张拉顺序见表2，每次同时张拉东西两侧2根吊杆。

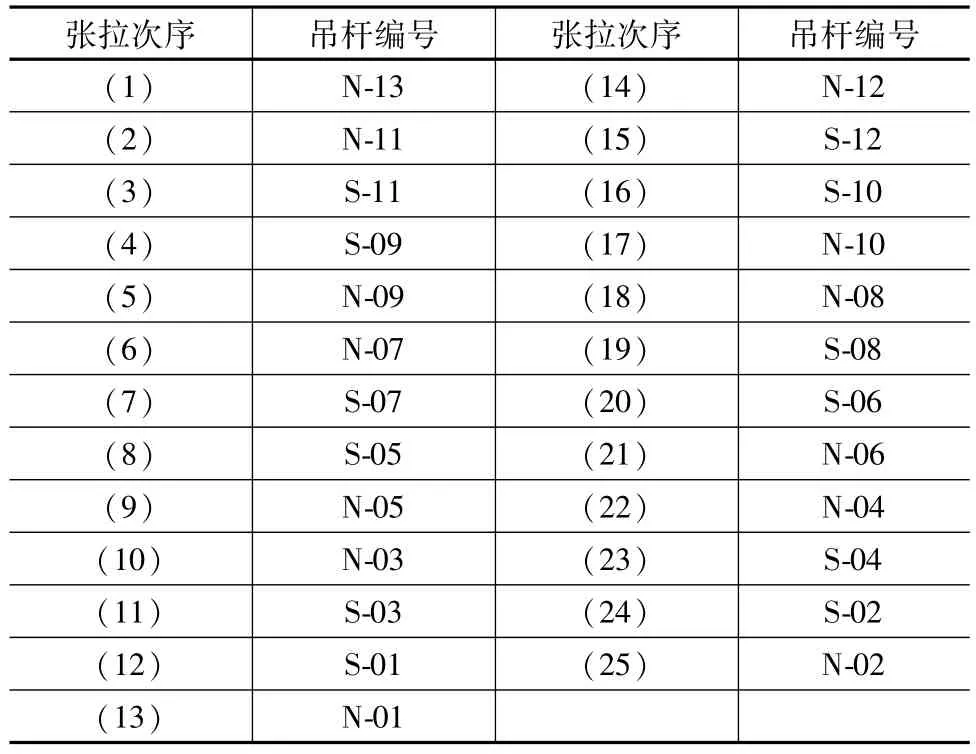
表2 张拉次序

根据式（6）、式（7），解得第一次迭代结果的索力调整向量｛T1｝，则调索时需要在原有吊杆力上增加的索力值用向量｛D1｝表示。由于影响矩阵［A］由每根吊杆增加10 kN的荷载求得，因此｛D1｝＝10｛T1｝，经整理得：

将上述第一次迭代计算结果各吊杆索力的调整值按照实际吊杆张拉顺序导入ANSYS计算模型中，可得到每根吊杆在第一次迭代调索后的索力值结果，见表3，第1次迭代调索后索力结果和目标索力比较见图5。

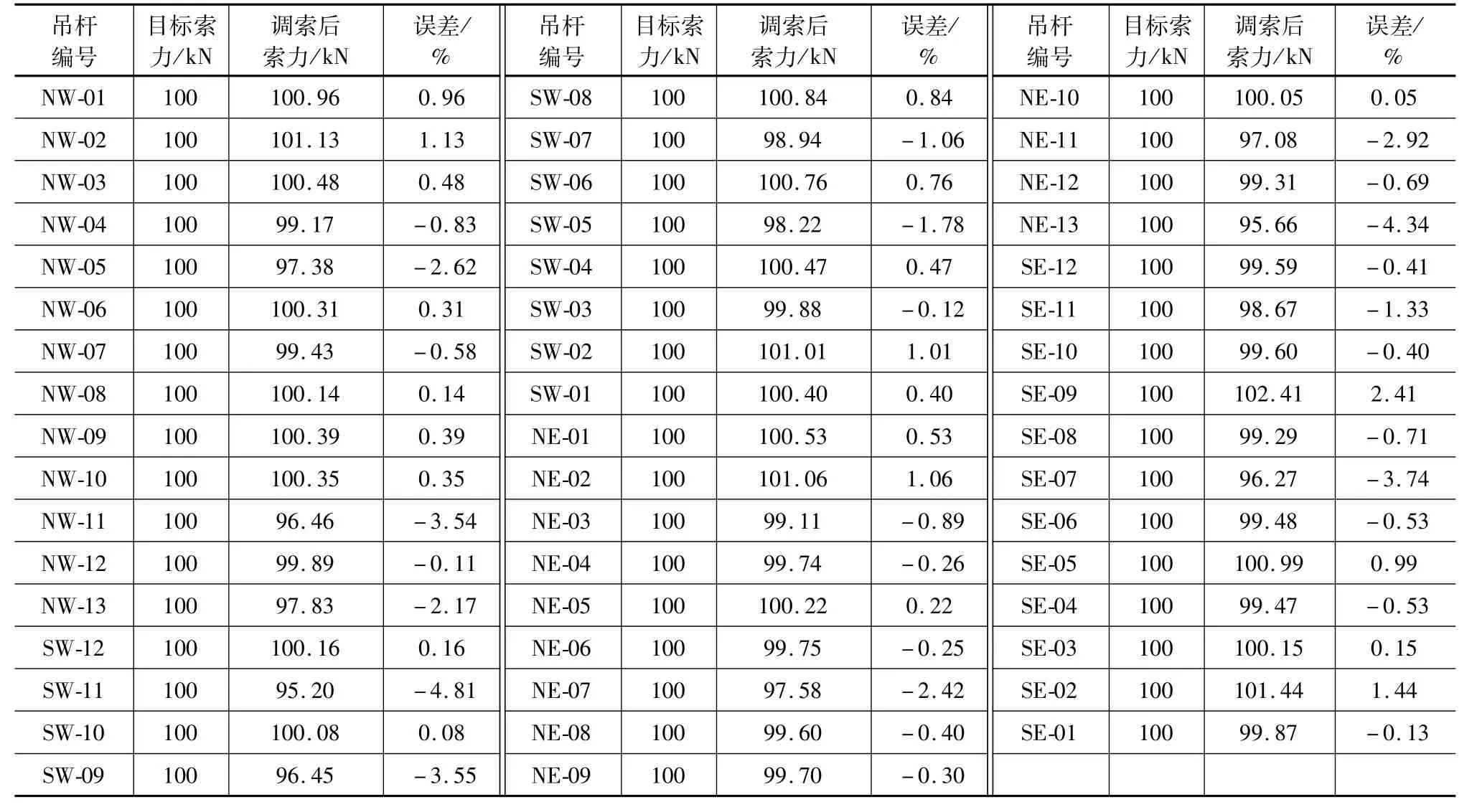
表3 调索计算结果

图5 第1次迭代调索后索力结果和目标索力比较

基于影响矩阵法，本桥钢箱拱吊杆索力最大误差率绝对值由最大44.33%降至4.81%，能够大幅降低索力调整的误差率，满足成桥施工验收的控制要求。影响矩阵法考虑吊杆张拉顺序，不需要试凑，也无需第三次张拉调整，通过求解矩阵的方法得到一组吊杆张拉值，进行多次迭代即可得到目标索力的调整量，达到目标吊杆索力要求。