考虑风险偏好的网络舆情预警模型*——基于直觉模糊和Choquet积分
2021-11-05陈福集谢加良
林 玲 陈福集 谢加良 李 凤
(1.福州大学经济与管理学院 福州 350108;2.集美大学理学院 厦门 361021;3.集美大学大数据建模与智能计算研究所 厦门 361021)
0 引 言
最新发布的《第46次中国互联网发展状况统计报告》显示,截至2020年6月,中国网民较2020年3月增长了3 625万,互联网普及率达67.0%,网民规模达9.40亿。国内互联网产业蓬勃发展。由于互联网信息平台的触手可及和公众开放言论自由,部分网民在纷繁芜杂的海量网络信息中,缺失判断能力,易被不良的舆论所误导,在意见领袖和网络推手的操纵下,可能频繁引发网络舆情,激发社会矛盾。准确地把握网络舆情发展态势,及时对网络舆情事件进行危机评估实时预警,能为政府对突发舆情事件进行合理管控提供有力决策支持,有助于营造良好网络生态,维护国家安全和社会和谐稳定。
网络舆情预警研究是舆情研究热点之一,其主要涉及到预警指标体系的筛选和预警模型的构建两方面。预警指标的分析与筛选主要从以下几个角度进行:a.从网络舆情整体特性出发的指标筛选[1];b.从具体事件性质出发的指标筛选[2];c.从不同媒介角度出发进行指标筛选等[3]。舆情预警模型的构建主要通过熵权法、层次分析法等确定各指标主客权重[4],运用各种数理模型或机器学习的方法,如:灰色关联[5]、模糊综合评价[6]、模糊推理模型[7]、人工神经网络模型[8]、支持向量机[9]等,对采集的评价指标信息进行融合、综合评判或推理预测[10-11],从而得出网络舆情的不同风险等级,为政府的舆情管控提供决策支持。
网络舆情预警模型相关研究取得了丰硕成果,但还可以进一步改进和完善,主要有如下四个方面:a.网络舆情预警风险评估过程中,由于领域专家自身相关知识的局限性和所能掌握的信息的模糊性和不完全性,难以给出相应的精确评价值,而模糊理论与决策方法能够充分弥补这方面的不足;b.网络舆情预警模型的指标之间存在关联性,评价过程中需要考虑属性之间的交互性以获得更客观的综合评价[12];c.已有研究较少考虑到决策者主观的心理因素,而网络舆情预警评估属于风险评估范畴,决策者不同的主题情景下,往往会基于主观认知的行为特征,带有明显的风险偏好[13-14],尤其对于涉政、涉警,可能影响国家安全与稳定的舆情话题,专家在评估过程中通常会表现出明显风险规避倾向;d.不同领域专家,由于背景知识与经验阅历有所差异,合理集结不同专家评价意见才能得到客观准确的评价结果。
本文构建网络舆情预警模型评价指标体系,提出一种基于直觉模糊Choquet积分,考虑专家风险偏好的网络舆情预警模型。首先,采用直觉模糊数表征网络舆情态势指标评价信息的模糊性与不确定性,考虑指标信息的关联性,利用Choquet模糊积分对评价指标值进行综合;其次,定义网络舆情风险偏好因子,计算不同专家对网络舆情风险等级的评估得分;最后运用投影法确定专家权重,合理集结各专家的评价信息。
1 相关理论基础
1.1直觉模糊集网络舆情预警评价体系中的各项指标难以用精确值来度量。如对主题敏感度、主题扩散趋势、传播媒体的影响力的评价信息具有明显的模糊性和不确定性。传播速度、公众参与度、态度倾向等指标虽有可参考的细分量化指标可供参考,但其在不同的舆情主题背景、不同的社会情境,和舆情发展的不同阶段下,其测量值的参考标准难以统一,所涵盖的信息量也有会所不同,加上专家领域背景知识存在不同程度的差异,其给出的指标评价值具有明显的不确定性。直觉模糊数能保留较多的决策信息,较好地匹配了决策者的模糊认知特点。
直觉模糊集(Intuitionistic Fuzzy Sets)由Atanassov[15]提出,它能够描述隶属度、非隶属度,和犹豫度的信息,较适合于处理不确定性问题,为决策者进行决策提供了适度弹性。

(1)
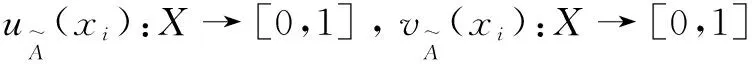
定义2[17]:设α=
1.2模糊测度与Choquet积分定义3[18]:设P(X)为X={x1,x2,…,xn}的幂集,给定ρ∈(-1,∞),μ:P(X)→[0,1],若满足如下条件,则称μ为定义在X上的模糊测度:
(1)μ(∅)=0,μ(X)=1
(2)若B,C∈P(X),B⊂C,则μ(B)≤μ(C)
(3)∀B,C∈P(X),B∩C=∅,有μ(B∪C)=μ(B)+μ(C)+ρμ(B)μ(C)
若X为某一多属性决策问题的指标集,则对于B,C∈P(X),μ(B)和μ(C)可认为是属性B和C的权重。
若ρ=0,则μ(B∪C)=μ(B)+μ(C),表明属性B和C相互独立;
若-1<ρ<0,则μ(B∪C)<μ(B)+μ(C),表明属性之间存在冗余关系;
若ρ>0,则μ(B∪C)>μ(B)+μ(C),表明属性之间存在互补关系。
定义4[19]:若f为定义在非空集合X上的模糊测度,αi为定义在X上的一组模糊数,则αi(i=1,…,n)关于模糊测度f的Choquet积分算子为
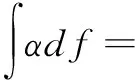
(2)
其中,(i)表示为向量α(i)上的置换,满足0≤α(1)≤…≤α(n),同时有
A(i)=(x(i),x(i+1),…,x(n))且A(n+1)=0
如果αi=
(3)
1.3考虑风险偏好的直觉模糊得分函数网络舆情预警指标的评估过程中,专家评价值的犹豫度对风险追逐着意味着潜在的风险越小;而对风险厌恶者来说,可能存在的风险越大,尤其是对于主题敏感的舆情话题,专家通常更偏向于风险保守。因此,在考虑犹豫度的潜在风险主观特征,引入基于风险偏好的直觉模糊得分函数。
定义5:设α=
(4)
其中,πα=1-uα-vα为犹豫度,η∈[-1,1]为风险偏好因子,在网络舆情预警风险评价中,η<0时,表现为风险偏好;η>0表现为风险厌恶;η=0时,则为风险中立,此时sη(α)=uα-vα
定义6:设两个直觉模糊数α1,α2,由定义5基于犹豫度的风险偏好,则:
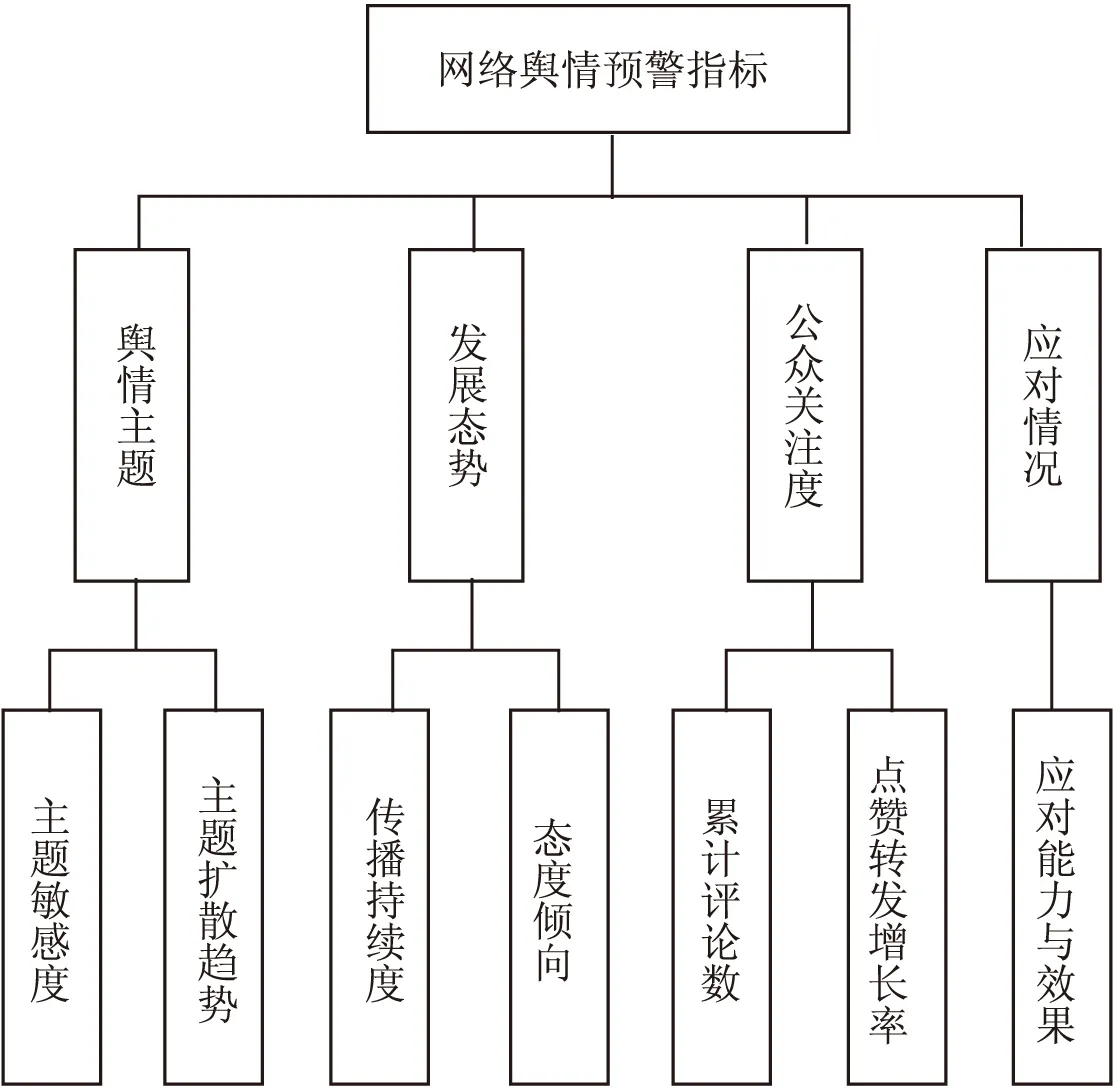
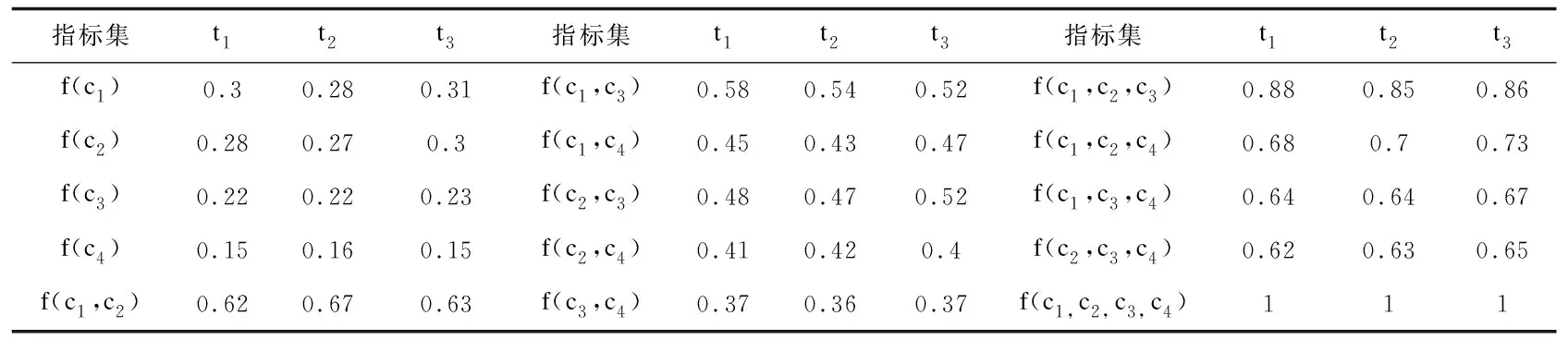
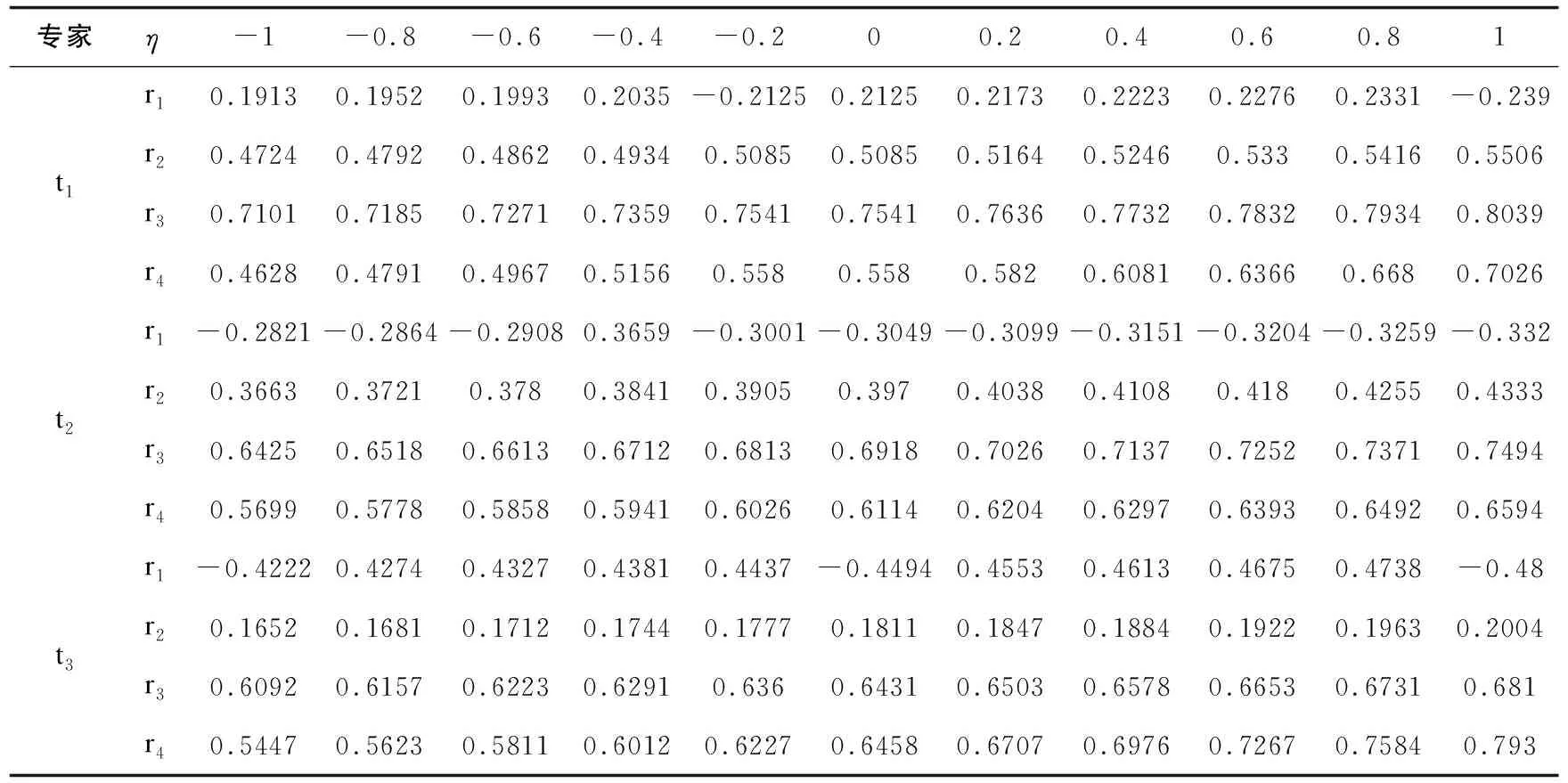
若得分函数sη(α1) 若得分函数sη(α1)>sη(α2),则α1>α2 若得分函数sη(α1)=sη(α2),则α1~α2 2.1网络舆情预警指标体系的构建网络舆情预警指标体系的构建主要通过选取少量的,能综合表征了网络舆情发展态势的,各个维度的可评估层次指标,使决策者能够通过指标体系,从各个维度实时监测网络舆情的发展演化趋势,挖掘网民的情感倾向,分析其潜在的风险因素。指标评价值可以参考网络客观采集的数据,也可以让专家根据实际情况基于领域知识和经验进行评估。指标的选取需要遵循科学性、系统性、简明性、易量化等原则,应能体现网络舆情中本质、核心的信息[20-21]。本文在已有研究的基础上确定了主题敏感度、主题扩散趋势、传播持续度、态度倾向、累计评论数、点赞转发增长率和应对能力和效果共7个指标,并归纳出舆情主题、发展态势、公众关注度、应对情况等4个一级指标,从而构建网络舆情预警模型的指标体系如图1所示。 图1 网络舆情预警模型指标体系 主题敏感度:反映公众对舆情话题的关注度,主题越敏感,风险越高,如高敏感度的涉政舆情可能危及国家安全与社会稳定。 主题扩散趋势:舆情主题可能涉及到相关领域或人物的广度,影响的深度,以及话题是否具有易于引发连锁反映、多点爆发、快速扩散等特点。该指标不仅取决于舆情主题特点,和所涉及人物的影响力,而且要结合当前舆情发展态势进行判断。 态度倾向:公众对舆情主题所持的观点倾向,通常分为正、负和中立3种立场,可通过对社交平台的负面评论的占比来进行量化。 传播持续度:反映舆情主题受关注的持续时长,主要体现在媒体报道的数量和频率,以及公众参与的持续变化情况。如果舆情主题持续受关注,且热度不减,其爆发的可能就越大,风险等级越高。 累积评论数:观测公众参与度的指标,数据采集主要来源于各大门户网站、微博、热门论坛当中对主题相关文章和帖子的评论数。 点赞和转发增长率:单位时间内公众对舆情主题参与的变化情况,反映舆情传播的速度,反映公众对舆情事件的态度倾向、主动参与传播的欲望。 应对能力与效果:网络舆情涉及的应急部门对舆情突发事件的快速反应能力与效力。及时对公众的质疑做出适当反映,发布相关权威信息,有利于疏导公众负面情绪,对防止舆情危机升级有积极的作用,在指标体系中为负向指标。 2.2基于直觉模糊Choquet积分的网络舆情预警模型为便于表述,定义如下描述符以表示网络舆情预警评价过程中所涉及的相关集合和变量。 C={c1,c2,…,cn}:n个网络舆情预警评价指标的集合,其中cj表示第j个指标,j=1,2,…,n。 R={r1,r2,…,rm}:m个网络舆情风险等级,ri表示第i个网络舆情风险等级,i=1,2,…,m。 T={t1,t2,…,tl}:l位对舆情预警体系指标进行评估的专家,其中tk表示第k个专家,k=1,2,…,l。 2.2.1 网络舆情预警指标直觉模糊评价矩阵 邀请l位各个领域专家,对网络舆情预警模型的各个一级指标进行风险评估,可参考二级指标实时获取的数据,结合专家的领域知识和经验。假设对一级指标采集各位专家的直觉模糊评价值为 (5) (6) 综上所述,基于直觉模糊Choquet积分的网络舆情风险预警步骤如下: 步骤1:针对网络舆情事件,邀请领域专家按照预警指标体系一级指标,给出直觉模糊评价值,同时对指标幂集权重给出评估值。 步骤2:根据专家给出直觉模糊评价矩阵和指标权重评估值,运用直觉模糊Choquet积分算子,算出各位专家对网络舆情风险等级的直觉模糊综合评价值。 步骤5:综合专家基于不同风险偏好的综合评价得分和专家的权重向量,对专家意见进行集结,求得舆情预警的最终风险等级评价结果。 某舆情事件开始在网上流行传播,将网络舆情风险等级分为r1、r2、r3、r4四级,分别对应I级(低)、II级(中)、III级(高)、IV级(极高),邀请网络舆情研究领域和公共管理领域的3位专家对网络舆情风险进行研判。按照前述构建的网络舆情预警模型指标,结合当下实际局势,参考二级指标所获得的数据,专家t1、t2、t3分别根据自身的领域知识和经验,给出4个一级指标属性的直觉模糊评价值,如表1至表3所示。 表1 专家t1的评价值 表2 专家t2的评价值 表3 专家t3的评价值 针对评价指标的重要性和指标之间的关联性,专家t1、t2、t3分别给出一级指标幂集的权重评估值,如表4所示。 表4 专家t1、t2、t3的评价值对指标集幂集权重的评估值 以专家t1为例,评价网络舆情对应于各风险等级隶属情况。对风险等级r1,专家t1给出各属性的直觉模糊评价值如表1所示,按从小到大排序如下: 根据公式(3),运用直觉模糊Choquet积分算子计算网络舆情对应于风险等级r1的直觉模糊评价值为 ={(1-(1-0.10)(1-0.62)×(1-0.25)(0.62-0.48) ×(1-0.50)(0.48-0.22)×(1-0.50)0.22,(0.80)(1-0.62) ×(0.60)(0.62-0.48)×(0.40)(0.48-0.22)×(0.40)0.22)} =<0.3384, 0.5509> 依次可求得可得专家t1对该网络舆情隶属于其他风险等级的直觉模糊评价值: 同理,计算其他专家对该网络舆情事件风险等级的评价值,从而得到三位专家对该网络舆情风险等级的综合评价直觉模糊值如表5所示。 表5 专家t1、t2、t3的综合评估值 根据现场问卷调查评估情况,专家t1、t2、t3的风险偏好因子η分别设定为:(0.8,0.5,0.7),由公式(5),得到各专家基于风险偏好的该舆情风险综合评价得分如表6所示。 表6 基于风险偏好的专家t1、t2、t3的综合评价得分 运用投影法(第2.2.3节)求得t1、t2、t3三位专家的权重向量为(0.3627,0.3252,0.3121),综合专家们最终意见,得到舆情风险等级评价结果为 其中最大得分值0.6606,对应风险等级r3,III级(高),因此,运用本预警模型对该网络舆情事件风险等级最终评判为III级(高)。 为进一步考查各专家的综合评价值的可靠性,对各专家的评价结果进行风险偏好灵敏度进行分析。设定风险偏好因子变化范围η={-1,-0.8,-0.6,…,1},得到3位专家基于风险偏好因子变化的舆情预警评价得分如表7所示。 表7 专家t1、t2、t3综合评价得分随η变化表 图2至图4的雷达图数据分别来源于表7三位专家的评价数值,图5的数据来源于表8专家综合评价数值。雷达图从圆心径向向外是评价值从小趋大的过程,对应舆情不同等级用4种线型,不同颜色呈现,评价值高的等级线则会出现在最外圈,随着风险偏好因子η值在圆周上顺时针从小到大变化,从图中可看出,专家的评价结果可能发生变化。图2和图3显示,专家t1、t2对舆情风险的综合评价得分结果均r3,对应风险等级为III级(高);图3显示,专家t3的评价结果随风险偏好因子变化表现较为明显,当风险偏好因子η<0时,其判定结果为III级(高),结果与专家t1、t2相同,而当风险偏好因子η>0时,专家t3评价结果为舆情等级风险为IV(极高)。再对3位专家评价的直觉模糊评价值进行加权求和,其评价值对应的雷达图如图5所示,可以看出,随着风险偏好因子值的增大,专家的综合评价结果趋向于IV级(极高)。 表8 三位专家评价的加权求和值随η变化表 图2 专家t1评价随η变化得分雷达图 图3 专家t2评价随η变化得分雷达图 图4 专家t3评价随η变化得分雷达图 图5 三位专家评价加权值随η变化得分雷达图 综合以上专家评价数据图表可以看出,该舆情主题敏感度较高,发展态势较快,公众有明显的负面情绪倾向,但当前相关部门的应对效果不明显。有比较谨慎的风险厌恶型评判专家(t3)认为,该网络舆情事件可能风险极高,必须引起特别重视。因此,综合专家总体意见,该舆情事件风险较高,且有可能进一步升级。针对该网络舆情事件,有关部门需要重视,积极采取措施,实时公布相关权威信息,及时疏导民众情绪,同时适当对传播媒介予以有效管控,对网络推手和意见领袖进行严格监管,禁止其发布误导性、煽动的言论,必要时应当采取强制措施,防止舆情事件往极端方向演化。 网络舆情监管形势日益严峻的生态环境下,舆情预警模型应为政府的有效应对提供有力的决策支持。本文主要做了如下工作:a. 构建网络舆情风险预警评价指标体系,采用直觉模糊数表示专家对网络舆情风险评价属性值的不确定性,利用非可加模糊测度刻画指标之间的关联和交互关系,并通过Choquet直觉模糊积分算子对指标评价信息进行综合;b.考虑到不同领域专家对舆情特点的风险偏好,引入直觉模糊风险偏好因子,从而计算专家对当前舆情风险等级的评价得分;c.运用投影法确定各专家权重,进而综合专家的舆情风险等级的评价得分,最终得到网络舆情风险的预警等级; 互联网技术日新月异,网络舆情风险预警模型不断推陈出新。本文研究还存在不足之处:第一,对客观数据信息收集环节体现不足;第二,指标信息的智能融合与推理还有待进一步研究。因此,基于大数据技术的网络舆情信息抽取,借助专家知识库的模糊推理和信息融合,将是下一步网络舆情预警系统的研究方向。2 直觉模糊Choquet积分网络舆情预警模型


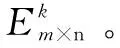
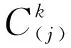
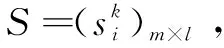
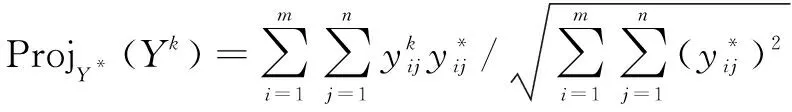
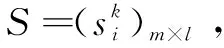
3 算例分析





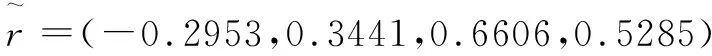


4 结 论
