基于电液直驱的动力踝足假肢对行走步态的影响

2021-11-05黄其涛李博文刘华健

哈尔滨工程大学学报 2021年10期

黄其涛，李博文，刘华健

(哈尔滨工业大学机电工程学院，黑龙江哈尔滨 150001)

目前全球范围内有超过600万的下肢截肢患者，受医疗水平限制，穿戴假肢是他们恢复直立行走主要手段。传统假肢是一个无源装置，可以通过弯曲脚掌储存一定能量[1]，其具有价格低、重量轻等优点，但无法提供额外的动力。研究表明，对于快速的行走运动需要踝关节主动对人体做功[2]，但使用被动假肢会让下肢截肢患者的行走速度更缓慢，并且会通过髋关节代偿发力来补偿踝关节的动力缺失，在这种运动模式下截肢患者的能量消耗需增加30%左右量才能达到与健全人体相近的行走速度[3]。

为了更好地满足患者的需求，研究者尝试了多种不同的控制策略[4]和驱动方式来更大程度地还原踝关节的特性，包括但不仅限于气动[5-7]、电机丝杠传动[8-11]以及液压驱动[12]。受限于功率质量比以及续航能力，现阶段动力踝足假肢系统商业化程度相对较低，多数处于原型机阶段，其最主要的技术难题是在约2 kg的终端质量限制下实现每千克体重高达2.5 W的峰值功率和1.6 N·m的最大扭矩输出能力[13]。电液直驱系统(electro-hydrostatic actuator,EHA)是一种广泛应用于航空领域的伺服驱动方式，该方式具有功率密度大、效率高的优点，其力位可控性较好，这些优势是使其在动力踝足假肢领域具备应用的基本条件[14]。英国巴斯大学的于天博士在商业化的被动智能假肢Elan foot[15]的框架下引入了电液直驱技术，研制了一款主被动混合假肢[16]。在前期研究过程中，本团队采用类似的理念研制了一款原型样机(MK-I)[17]，其能够在支撑相末期提供主动出力和主动复位，但由于内泄露等原因，无法提供足够的缓冲阻抗，帮助人体重心前移，在被动阶段的步态特性较差，且结构过于复杂，可靠性和维护成本难以保证。

在此基础上，本文提出了一种新型动力踝足假肢系统方案，该方案基于电液直驱技术设计驱动装置，并在模拟脊髓反射的肌肉骨骼模型前馈控制器[18]的帮助下，实现主动阻抗调节、净出力以及关节复位等功能，简化机械结构的同时优化性能。本研究以预采集的人体踝关节生物动力学数据样本作为参数优化调节的基础和实验对照组，将仿真加载实验的结果与其进行对比，论证动力踝足假肢系统方案的可行性以及对截肢患者步态的改善情况。

1 动力踝足假肢系统

1.1 动力踝足假肢系统设计

本文所采用的动力踝足假肢系统是基于本研究团队所研制的MK-I原型样机的改进方案，其整体结构如图1(a)所示。脚掌参考了较为成熟的Flex-Foot的结构设计，由碳纤维材质制成，能够起到像被动假肢一样的吸震缓冲作用。液压缸集成在小腿中，通过一个简单的滚动轴承铰链结构与脚掌相连，与联接轴和活塞杆构成了一个平面四杆机构。脚掌可以在有限的范围内绕小腿做定轴转动，模拟人体踝关节在矢状面内单自由度运动。

该系统的液压原理如图1(b)所示，高扭矩无刷直流伺服电机(Maxon ECi-40 48V)直接驱动双向齿轮泵(VIVOLO XV-0R/0.98)作为整个系统的动力核心，通过集成在阀块中的管路将液压油直接送入液压缸两腔，最大程度地减少不必要的管路损失。由于该系统是闭式结构，为了防止气穴现象的发生，在回路中添加了由蓄能器和液控单向阀所组成的补油装置。上述零部件都集成在特殊设计的微型阀块中，并直接安装于小腿后部，由背包中的锂电池供能，以满足踝足假肢的生理体积限制。

图1 动力踝足假肢系统三维结构及液压系统原理Fig.1 Mechanical structure and hydraulic circuit diagram of the EHA powered ankle-foot prosthesis

此外，该踝足假肢采用NI公司所出品的cRIO系统作为控制器，通过附加的ADC/DAC模块进行传感器信号采集和控制信号输出。踝关节角度通过磁性角度传感器(micro-epsilon MDS)采集，一对油压力传感器(variohm EPT1200)分别安装于齿轮泵的出入油口，采集液压缸两腔压力差，以实现闭环力控制。控制器输出的驱动信号通过伺服控制器(ESCON 50/5)放大并驱动无刷电机，该驱动器还可以同步采集电机的转速和电流信号，并返送到cRIO系统，便于进行后期数据分析处理。

1.2 控制系统组成

控制系统的设计理念是使得受控踝足假肢控制系统设计的基本原则是使得截肢患者穿戴假肢在平地行走或者斜坡行走过程中实现近似健全人体的功能。由于下肢假肢在行走时更多的属于从动机构，并且人的行走速度是不断变化的，无法使用位置控制来实现步态控制，因此，还原健全人体在支撑相所体现出的阻抗特性是踝足假肢最为关键的被控对象。本文通过基于设计肌肉骨骼模型的前馈控制器，以角度传感器采集的关节角度为输入生成关节转矩指令，以PD控制律的力控制器来降低跟随误差，实现达到近似还原踝关节性阻抗特性的目的。

以健全人体矢状面内的肌肉骨骼基本构造为基础设计了等效的前馈模型，如图2(a)所示。骨骼用2个连杆与一个回转副表示，小腿后部肌群和跟腱则由希尔肌肉模型来代替。当脚掌处在前支撑相和摆动相时，该模型具有单向出力特性，只能提供拉力。为构成拮抗驱动器，并根据实际的腿部结构简化模型，引入弹簧阻尼模型来实现对胫骨前肌的替代。上层控制则由有限状态机实现。有限状态机通过检测角度传感器以及压力传感器的反馈值来判断人体处于步态周期中的哪一个阶段，进而选择肌肉模型的工作状态。总的输出是由肌肉模型与弹簧阻尼模型所生成的扭矩之和。

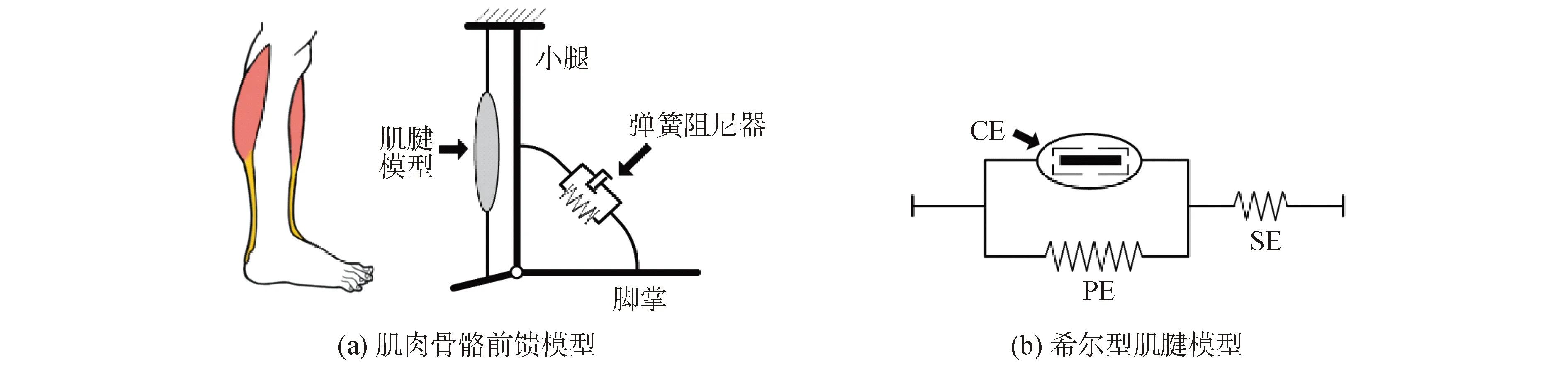
图2 肌肉骨骼前馈模型及肌腱模型Fig.2 Musculoskeletal feedforward model and Hill-type muscle-tendon structure unit.

1.2.1 肌肉骨骼模型

肌肉骨骼模型是在的希尔型肌肉模型的基础上加入模拟脊髓反射的力正反馈激励构成，是生成踝关节阻抗特性的主要来源，也是整体前馈模型中的重要部分，如图2(b)所示。肌肉模型由以下部分组成：用于描述肌肉组织、具有主动收缩能力的收缩元件以及用于模拟跟腱的弹性元件，另外还有用于表述与人体肌肉结缔组织相同功能的2个单向并联弹簧[2]，但并联弹簧在本文涉及的研究范围中这2个元件输出较小，因此在设计控制系统时选择忽略这2个元件。

收缩元件的出力大小由其长度lCE、肌肉收缩速度vCE和激励度A所决定[19]。收缩元件的最终出力FCE可以表示为[20]：

FCE(lCE,vCE,A)=FmaxfL(lCE)fV(vCE)A

(1)

收缩元件的输出与长度的关系fL(lCE)，可由钟形曲线描述[21]，收缩元件的出力与其收缩速度的关系fV(vCE)则由扩展希尔公式[22]描述。被动弹性子模型SE结构相对简单，为一个单向的非线性弹簧，可以由分段函数描述[23]：

(2)

式中：ε=(lSE-lslack/lslack)是弹性元件的形变度；lslack是不受外力时的松弛长度；εref则是根据方程FSE(εref)=Fmax得到的参考形变度。由于收缩元件与弹性元件串联在一起，它们具有相同的出力FMTS(t)。因此，肌肉模型的出力可以由给定的肌肉长度lMTS(t)和激励度A(t)确定。

肌肉的激励度A是由神经信号STIM经过一个一阶惯性环节得到的。STIM的可由力反馈、长度反馈等方式生成，在本系统中则由力正反馈所决定[20]，如图3所示。力正反馈是脊髓反射，首先在猫身上被发现[24]，相关研究[25-26]表明同样适用于人体，可以实现近似于健全人体下肢出力的阻抗特性[20]。神经信号STIM(t)是由肌肉模型出力FMTS经过增益GRF放大，延时Δp=20 ms模拟脊髓反射的传导时间，最终设定一个初值STIM0以避免运算过程中出现奇点。

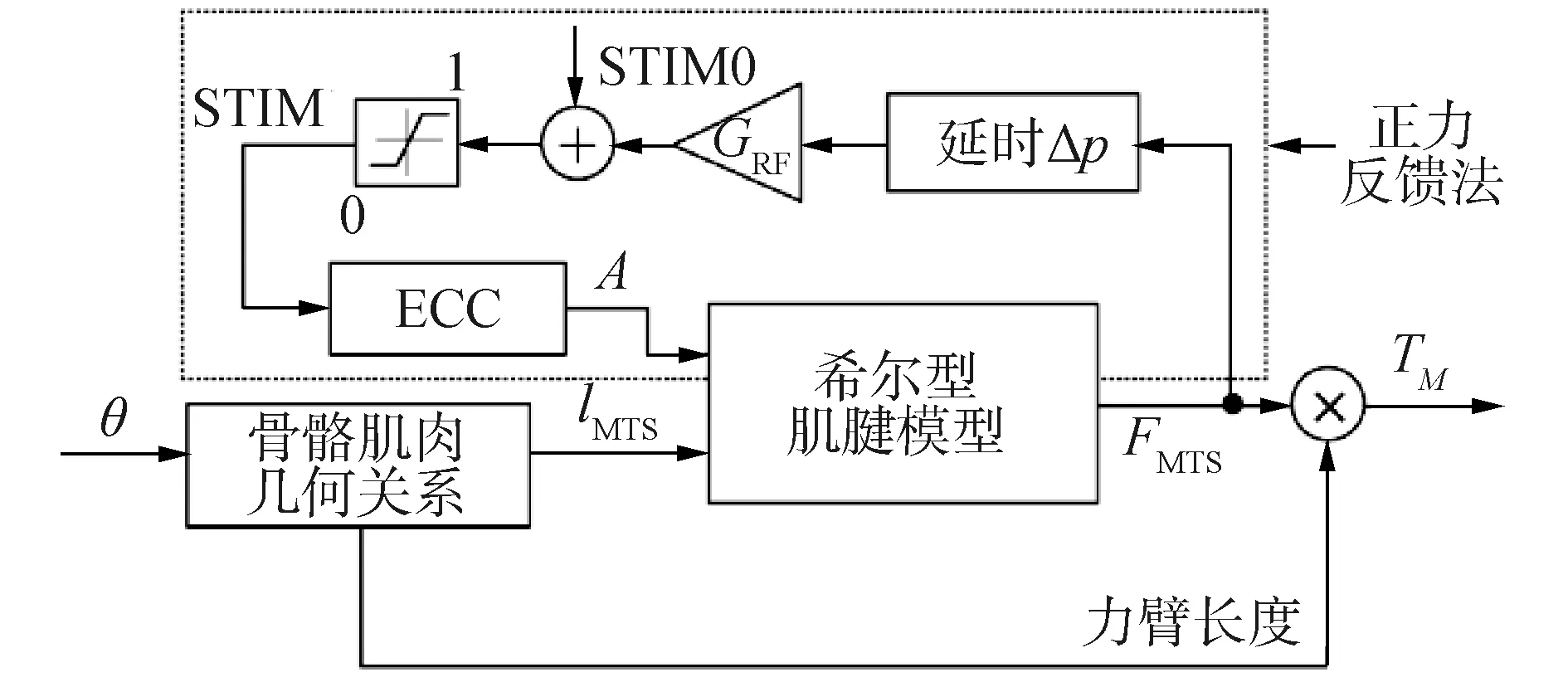
图3 神经肌肉模型自反馈机制以及关节角和关节扭矩间的对应关系Fig.3 Reflex scheme of the neuromuscular model representing the relationship between ankle angle and the MTS torque contribution

1.2.2 骨骼肌肉几何结构

在单一步态周期中，肌肉长度lMTS是由关节角度θ和图3(a)所示的肌肉骨骼模型的结构关系确定。关节角度θ为胫骨和前脚掌之间的夹角，脚掌与胫骨重合时为零位，运动方向以脚掌做背屈运动的方向为正。肌肉模型的长度变化量ΔlMTS可以表示为[27]：

ΔlMTS=rfootρ[sin(θ-φmax)-sin(φref-φmax)]

(3)

其中，ρ=0.5是羽状角系数，该系数用于表征由于肌腱与骨骼连接方式导致肌肉出力方向与肌肉排布方向不一致的程度。rfoot=0.05 m是跟腱在骨骼上的连接点到踝关节回转中心的距离，φref和φmax分别是lMTS等于其原长时和肌肉模型垂直于脚跟时所对应的踝关节角。同理，由肌肉模型产生的踝关节扭矩可以表示为：

TM=FMTScos(θ-φmax)rfoot

(4)

神经肌肉模型中的大部分参数都是有生物学领域研究结果所得出的典型值[18]，部分未详细说明的自选参数如表1所示。

表1 前馈模型部分参数表Table 1 Parameters of the musculoskeletal model

1.2.3 上层决策控制器

如前文所述，上层控制器用于控制子模型的工作状态，该控制器由有限状态机来实现。在本文所述的控制系统中，单一步态周期分为3个步态阶段，分别为：前支撑相、后支撑相以及摆动相。步态切换由有限状态机检测踝关节的角度和扭矩反馈信号并依据如图4中的切换原则选择模式。摆动相到前支撑相的转变以脚跟着地为切换点，该状态切换的阈值被设定为TP= -7 N·m(理论阈值为0 N·m)，切换阈值设定较高可以减少错误判断的可能。前支撑相到后支撑相之间的切换以弹簧阻尼模型的输出扭矩TD大于零作为依据，自一个周期内弹簧阻尼器的输出降为0后，则在该周期内弹簧阻尼器不输出扭矩。后支撑相与摆动相之间的过渡则相对较为复杂，因为踝关节扭矩在此过程中并非单调，因此，判断依据设定为关节扭矩TP在后支撑相曾经大于20 N·m、前支撑相的持续时间大于200 ms且满足以下2个判别条件之一：TP<5 N·m或者θ<-0.3 rad。关节扭矩的正方向规定为使得脚掌趋向背屈运动的方向。

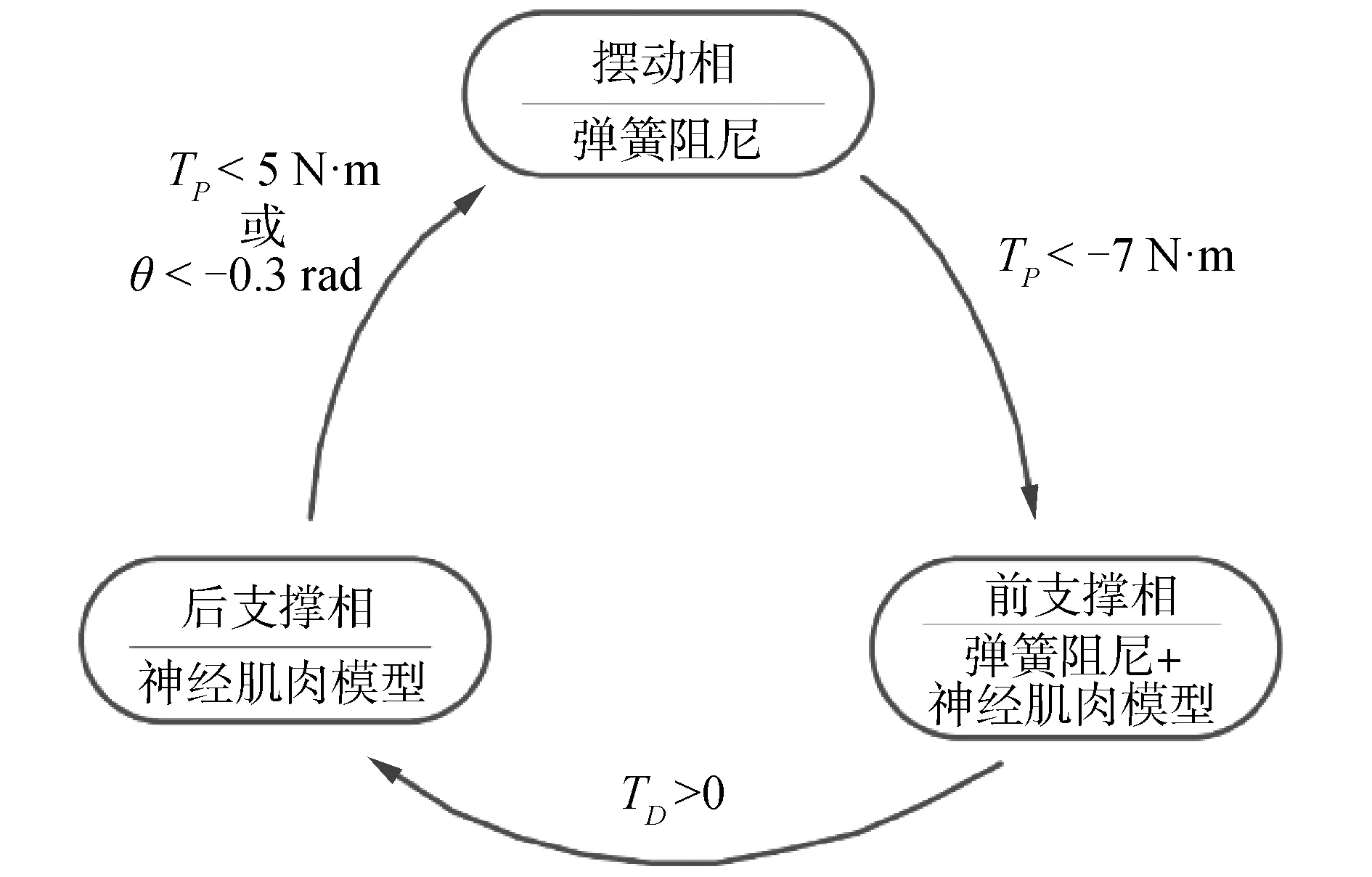
图4 基于有限状态机的上层决策控制器及判别条件Fig.4 Finite state machine with state transition thresholds

1.2.4 弹簧阻尼模型

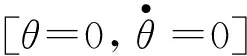
(5)

式中：KP是比例系数代表弹簧的刚度；Kd是微分系数表征阻尼的大小。由于弹簧阻尼模型在前支撑相和摆动相的工作模式不同，因此分别为2个阶段设置了不同的比例系数和微分系数。对于前支撑相来说，弹簧阻尼模型的主要作用是减缓冲击，经仿真调试参数，选取[KP=70 N·m/rad,Kd=6 N·ms/rad]可以获得较好的扭矩拟合效果。对于摆动相来说，弹簧阻尼模型事实上是一个PD控制率的控制器，用于减小跟随误差帮助脚掌复位，在摆动相阶段选取[KP=200 N·m/rad,Kd=7 N·ms/rad]以使得复位过程快速、平稳。

1.2.5 控制策略实施

由于神经肌肉模型是由多个数学公式表示，无法通过传感器采集的关节角度以及压力传感器值进行正向求解。在实际运用过程中，利用肌肉出力与肌肉收缩速度关系函数fV(vCE)的单调性得到其反函数vCE(fV)并构建代数环，设定一个肌肉收缩量的初值并以此来迭代求解来实时获取TM(t)的数值近似解。

将健全人体平地行走时踝关节角度样本(步速1 m/s)作为图3所示的模型的输入θ(t), 仿真结果如图5所示。将前馈模型输出的扭矩与健全人体的扭矩轮廓对比可知，前馈模型很好地还原了踝关节在中慢速平地行走时的扭矩轮廓，能够生成健人体所需的关节扭矩信号。

图5 一个步态循环周期中骨骼肌肉前馈模型扭矩输出对比Fig.5 Ankle torque contributed by each individual component of the feedforward model during a gait cycle

为了减小假肢系统跟随由前馈模型生成指令时的误差，控制系统中加入了一个PD控制律的控制器，如图6所示。前馈模型输出的扭矩信号先经过一个补偿系数Kc放大再与力传感器采集的反馈信号做差得到踝足假肢的控制信号。

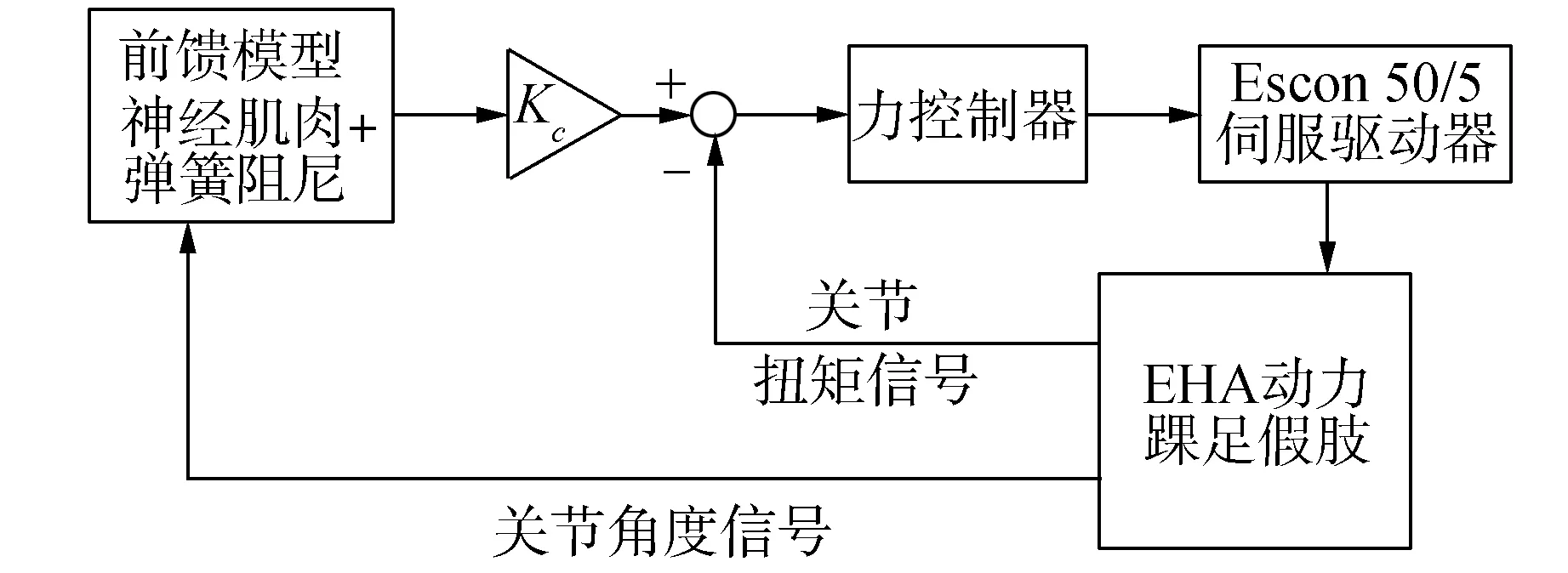
图6 动力踝足假肢系统控制架构Fig.6 Control architecture diagram of the EHA powered ankle-foot prosthesis

1.3 仿真实验拟定

根据人体踝关节相关参数，建立了踝足假肢系统的仿真模型，参照体重为75 kg的正常人体踝关节扭矩样本、体重为50 kg人体踝关节扭矩样本和穿戴被动假肢截肢患者的样本将作为仿真模型的输入和对照组。由于人体对于踝关节的负载可等效为在踝关节处产生的力矩，故本文将关节扭矩样本作为仿真模型的输入信号来模拟脚掌与地面接触时在踝关节处产生的关节扭矩，将一个周期内仿真模型得到的踝关节的角度与样本的角度进行对比可以验证所设计的动力踝足假肢系统的可行性以及其对于胫骨截肢患者的行走步态的改善程度。2组仿真实验应用了相同的肌肉骨骼模型参数，为了适应样本自身特性，对反馈增益系数GRF进行了少量的调整。另外，在2组对照实验中，在摆动相应用了不同的位置控制方式，样本一采用轨迹跟随的方式来获取更好的关节角度曲线和测试系统的位置跟随能力，样本2则采用了前文所述的弹簧阻尼器复位来模拟现实的使用情况。

2 踝足假肢仿真实验结果

2.1 踝关节角度

如图7所示为一周期内的踝关节角度仿真结果，在步态周期的支撑相期间，该动力踝足假肢的关节角度很好地复现了预采集的健全人体生物学样本。最大跖屈角(样本1：19.5°；样本2：12.7°)和最大背屈角度(样本1：9.67°；样本2：9.57°)略小于采集样本参考值(样本1：11.6°；样本2：10.6°；样本1：19.9°；样本2：15.8°)，且在前支撑相和动力跖屈阶段(约55%～65%)有着较为明显的偏差。在摆动阶段(约65%～100%)，对于踝关节角度偏差来说，采用轨迹跟随复位方式的结果明显优于采用弹簧阻尼器复位，但事实上摆动相进实现快速复位即可，人体对摆动相的角度跟随误差无过多要求。

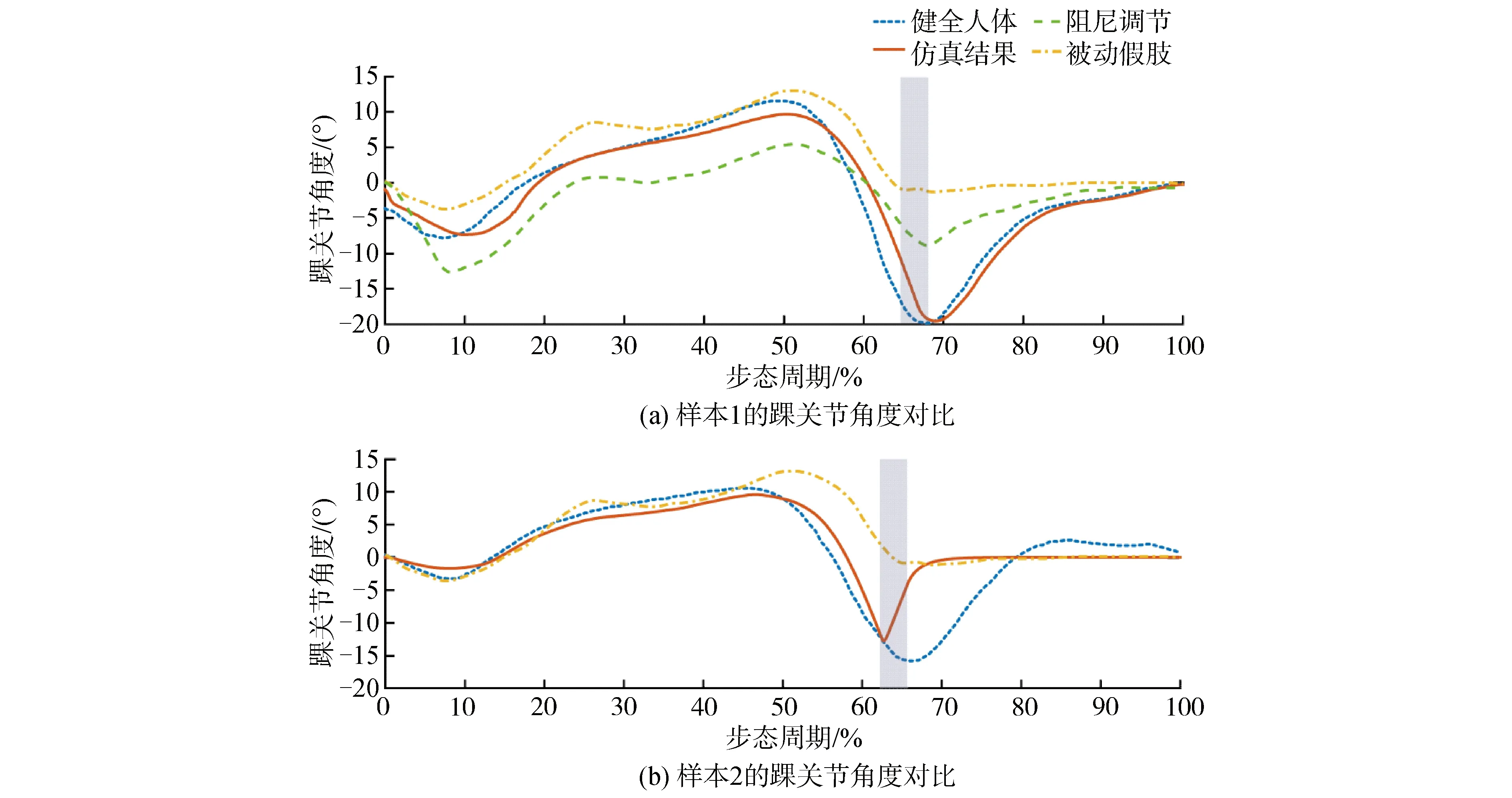
图7 仿真验证的关节角度及对比Fig.7 Simulation of ankle angle with comparison

2.2 踝关节阻抗特性

如图8所示为动力踝足假肢系统的角度-扭矩关系曲线，2个样本之间的阻抗特性差异较大，但其阻抗特性都为近似的非线性弹性特性。图中曲线的斜率代表着踝足假肢生成的刚度，曲线所包络的面积为一个周期内踝关节假肢对外做功大小。

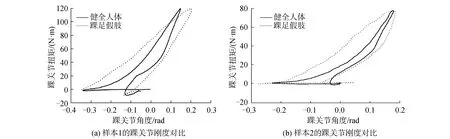
图8 仿真验证的假肢关节刚度对比Fig.8 Simulation of ankle stiffness with comparison

2.3 踝关节出力及能耗

如图9所示，在步态周期中，踝关节和假肢的负功率阶段代表假肢对人体的做负功，并提供必要的缓冲和阻尼。正功率阶段代表假肢对人体的正作用力，帮助人体重心向前移动，稳定步态。

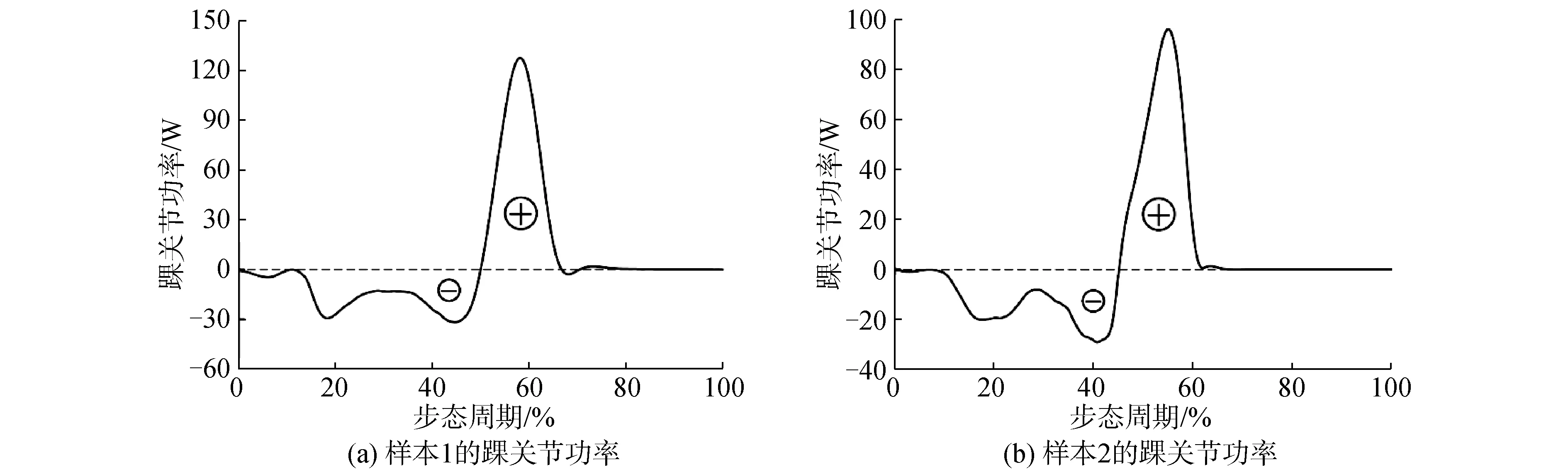
图9 仿真验证的假肢踝关节功率Fig.9 Ankle power output simulation with positive representing generation and negative representing absorption

3 踝足假肢仿真分析

由以上仿真结果表明，基于电液直驱的动力踝足假肢能显著还原人体踝关节的动态特性。与传统的阻抗控制系统相比，本文所设计的前馈模型在肌肉骨骼模型的帮助下可以得到更为平滑的关节角度曲线。在支撑中期阶段(25%～55%)比对照组更为明显。如图7所示，动力踝足假肢在还原后支撑相的动态特性方面相比传统被动假肢有着较大的优势，因为被动假肢所储存的能量无法满足后支撑相阶段蹬地时的高功率输出，这也直接被动假肢导致了后支撑相跖屈角严重不足，而动力假肢可以较好的补偿这一点。另外，最大背跖屈角并不是发生在脚尖离地的瞬间，而是在摆动相阶段。摆动相的目的是实现脚掌的快速复位，并不对最大跖屈角有要求，因此有少量的最大跖屈角不足是可以被允许的。

对于膝关节、踝关节等机器人的变阻抗特性系统，传统的阻抗控制策略是通过分段线性化来进行对非线性阻抗特性的拟合。在步态中选取特征点，将步态划分为若干阶段，并在每个阶段进行线性化，以达到变阻抗的目的。为了提高系统的稳定性和适应性，阶段划分不宜过于密集。否则在进行阶段切换时，必然会导致力指令信号的突变，进而导致冲击，导致步态中出现抖动的情况。而采用神经肌肉前馈模型对踝关节进行仿生建模，克服了分段线性化带来的一些问题，获得了非常自然光滑的关节曲线和较好的适应性。

仿真角度结果与生物样本之间的偏差主要发生在前支撑相和动力跖屈阶段。前支撑相的偏差主要是由于将胫骨前肌简化为弹簧阻尼模型所导致的。由于通过解算肌肉模型的步骤较为复杂，做出适当的简化可以提高系统的运算速度以保证控制系统的实时性。本文所选用的元件是在兼顾便携性和性能后的折衷，而且在模拟过程中没有对碳纤维脚掌进行计算。参照同类碳纤维脚掌的被动假肢，其可以在动力跖屈阶段释放能量，其具有在该阶段弥补峰值功率不足的问题。

由于液压系统本身具有阻尼特性，即使不具备主动输出功能也可以使得下肢截肢的患者步态更加自然，对于膝关节假肢也同样适用。但对于仅可调节阻尼的半主动假肢而言，可能由于泄漏而导致其不能提供足够的阻尼，但极低的能耗是它相对于动力假肢的较大的优势。本文所提出的动力踝足假肢可以实现半主动假肢所具备的功能，以适合中速行走与上下楼梯等踝关节出力相对较小的场合，以使整个系统能量消耗降低。