钢悬链线立管舷侧安装过程动力学仿真及耦合分析

2021-11-05昝英飞祝港袁利毫黄阔黄福祥罗超

哈尔滨工程大学学报 2021年10期

昝英飞，祝港，袁利毫，黄阔，黄福祥，罗超

(1.哈尔滨工程大学船舶与海洋工程学院，黑龙江哈尔滨 150001； 2.海洋石油工程股份有限公司，天津 300461)

钢悬链线立管是20世纪90年代初期提出的概念，随着世界第1条钢悬链线立管于1994年，由壳牌公司在墨西哥湾处的一座张力腿平台上安装完成[1]。钢悬链线立管引起了诸多学者的注意，为了增加钢悬链线立管使用的安全性，各国学者对钢悬链线立管展开了一系列研究降低钢悬链线立管使用风险。Mekha等[2]对PrinceTLP平台上钢悬链线立管设计过程中的设计和疲劳等难题进行分析，研究表明钢悬链线立管大偏离角有助于减轻钢悬链线立管在波浪中的疲劳损伤。Nakhaee等[3]研究了海床沟槽对钢悬链线立管动力特性的影响。吴剑国等[4]研究了浮体的慢漂运动对钢悬链线立管的影响。Duan等[5]对深水钢悬链线立管传递过程进行静力学分析，通过大挠度梁理论、Winkler地基模型和悬链线方法建立力学模型，重点研究了海床刚度、水深、初始安装角度等影响因素。数值分析结果表明，在钢悬链线立管传递过程中，较硬的海床会对钢悬链线立管产生较大的弯曲应力，海床刚度对钢悬链线立管的应力影响不大。初始安装角度越大，水深越深，弯曲应力会越小。Wang等[6]基于非线性大挠度梁理论建立深水缓波立管传递过程力学模型，基于有限差分法对传递过程中立管参数进行一系列数值分析，研究结果表明，立管触地点位置以及轴向张力均呈变化趋势。Bai[7]研究了钢悬链线立管的缩小比例模型动态测试，进行不同振幅和频率下的受迫振动分析，并用CABLE3D软件进行时域数值分析。研究结果表明平台平面内的运动与立管模型动力响应一致，触地点位置随着船舶偏移而改变，并且立管顶端和触地点有着较大的内力。石锦坤等[8]对钢悬链立管回接预铺设安装的关键过程进行静力学分析，得到绞车受力等数值结果，但其在研究过程中并未考虑环境与船舶运动影响。Zan等[9]提出了一种铺管船与管道耦合动力学模型，研究了耦合因素对铺管船和管道动力学的影响。Han等[10]基于“S”型铺设，提出了一种铺管船-缆绳-管道终端-管道的时域耦合模型，研究了管道终端设施在全耦合作用下的动力学特性。尤岩岩等[11]研究了平台激励下钢悬链线立管触地点附近的动力响应，研究结果发现，平台的垂荡运动对钢悬链线立管触地区响应影响最大、纵荡次之、横荡影响最小。

以上研究内容得出了诸多影响钢悬链线立管应力的结果，钢悬链线立管舷侧安装作为一种工程中新的钢悬链线立管安装方法，尚未有针对船舶-钢悬链线立管-收放(abandonment & recovery, A&R)缆多系统耦合动力学响应的数值仿真研究，本文依托于国内水深为1500级的陵水17-2工程项目，基于有限元法建立安装A&R缆与钢悬链线立管模型并进行舷侧安装过程仿真，分析在舷侧安装过程中A&R缆以及钢悬链线立管的弯矩与张力，以及安装作业船舶-钢悬链线立管-A&R缆在动力定位系统控制下的耦合因素影响。

1 钢悬链线立管舷侧安装作业

1.1 钢悬链线立管舷侧安装作业流程

钢悬链线立管布放一般可分为铺管——提管——移管3个过程[12]，其中提管过程是钢悬链线立管舷侧安装的主要过程，本文依托陵水17-2工程项目开展6"钢悬链线立管舷侧安装过程动力学仿真及耦合分析研究，本文以“海洋石油201”作为安装船进行钢悬链线立管的安装作业。立管提升作业如图1所示，提管过程首先需要“海洋石油201”船到达海床上的钢悬链线立管首端所在位置，通过舷侧系统垂直下放A&R缆连接海床上钢悬链线立管，然后继续下放A&R缆并驶离平台至安全距离后，向平台方向靠近，通过舷侧的管道回收系统回收A&R缆，将海床处的钢悬链线立管逐渐提升，直至“海洋石油201”船行驶至目标位置。

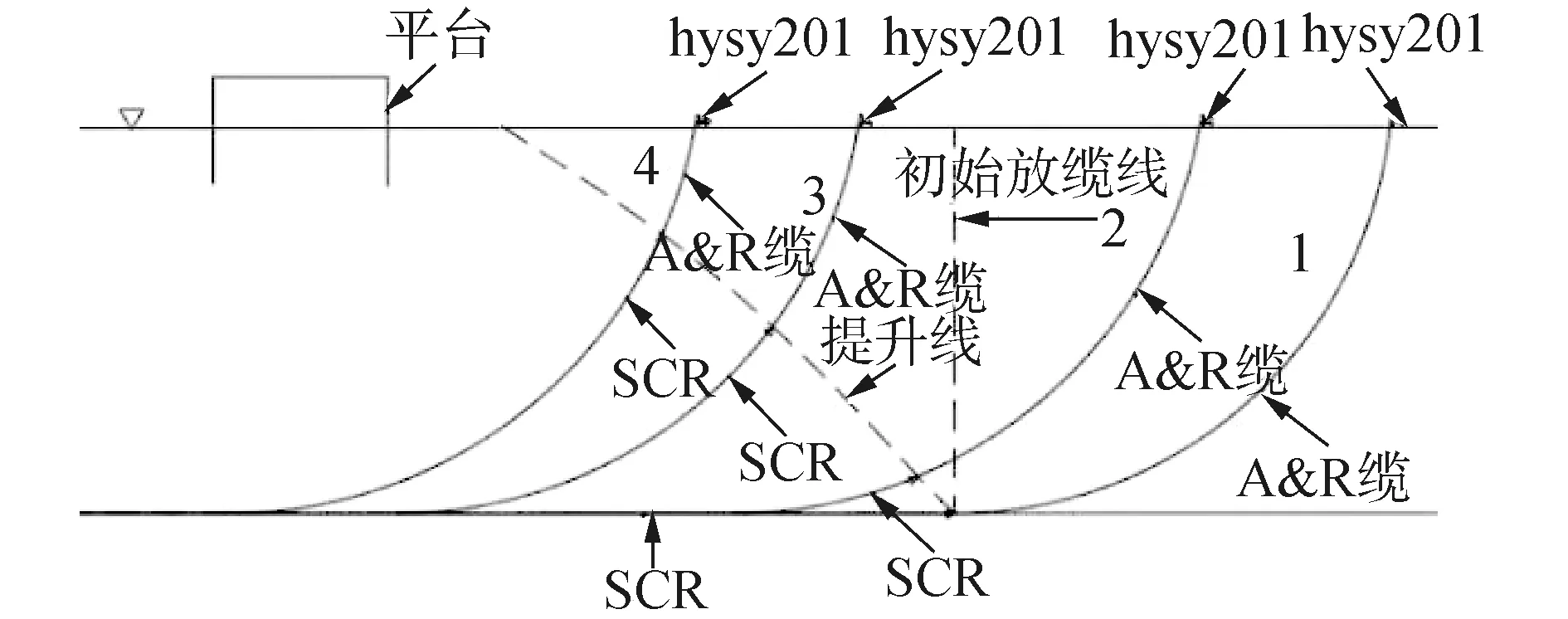
图1 钢悬链线立管提升作业流程Fig.1 Steel catenary riser lifting operation

1.2 主要设备参数

1.2.1 钢悬链线立管主要参数

本文选用钢悬链线立管型号为6"MEG(Monoethylene glycol)，管材为API-5L-X65的钢管。其主要参数如表1所示。

表1 6"钢悬链线立管主要参数Table 1 The main parameters of 6"steel catenary riser

1.2.2 A&R缆主要参数

A&R缆常用于深水作业，主要用于下放立管和回收立管，轴向刚度需保证在作业过程中不会轻易破损，A&R缆设计参数如表2所示。由于A&R缆的几乎没有弯曲刚度、剪切刚度和扭转刚度，可以忽略不计。

表2 A&R缆设计参数Table 2 The parameters of A&R cable

1.2.3 舷侧安装系统

舷侧安装系统位于安装作业船“海洋石油201”船左舷位置处，其作用是提升深水海底管道至适当位置。如图2所示，舷侧安装系统由2根支腿和一个横梁组成的框架结构、一组位于横梁中心的A&R缆滑轮、一个可以调整角度的柱状框架结构以及一个固定装置的柱状结构组成。在舷侧安装系统顶部滑轮处装有张力极限为400 t的绞车，通过调整角度，将A&R缆垂直下放至海底与立管进行连接，通过回收A&R缆完成立管的提升。

图2 舷侧安装系统Fig.2 The installation system

2 耦合仿真模型搭建

耦合仿真模型如图3所示，主要由安装船“海洋石油201”、A&R缆、6”钢悬链线立管3部分组成，耦合模型中的各部分都受到环境载荷的作用，“海洋石油201”船与A&R缆通过A&R缆顶端张力作用相互拖动，在A&R缆与6”钢悬链线立管间存在张力作用，除此之外，6”钢悬链线立管触地段还受到海床支撑作用。当“海洋石油201”偏离目标位置时，动力定位系统计算当前位置与输入目标位置得到偏差，计算各推进器复位需提供的推力，推力作用于船舶，船舶运动位置改变，钢悬链线立管与A&R缆轴向张力随之改变，新的循环产生，为保证船舶定位于目标位置，该循环系统会持续工作。

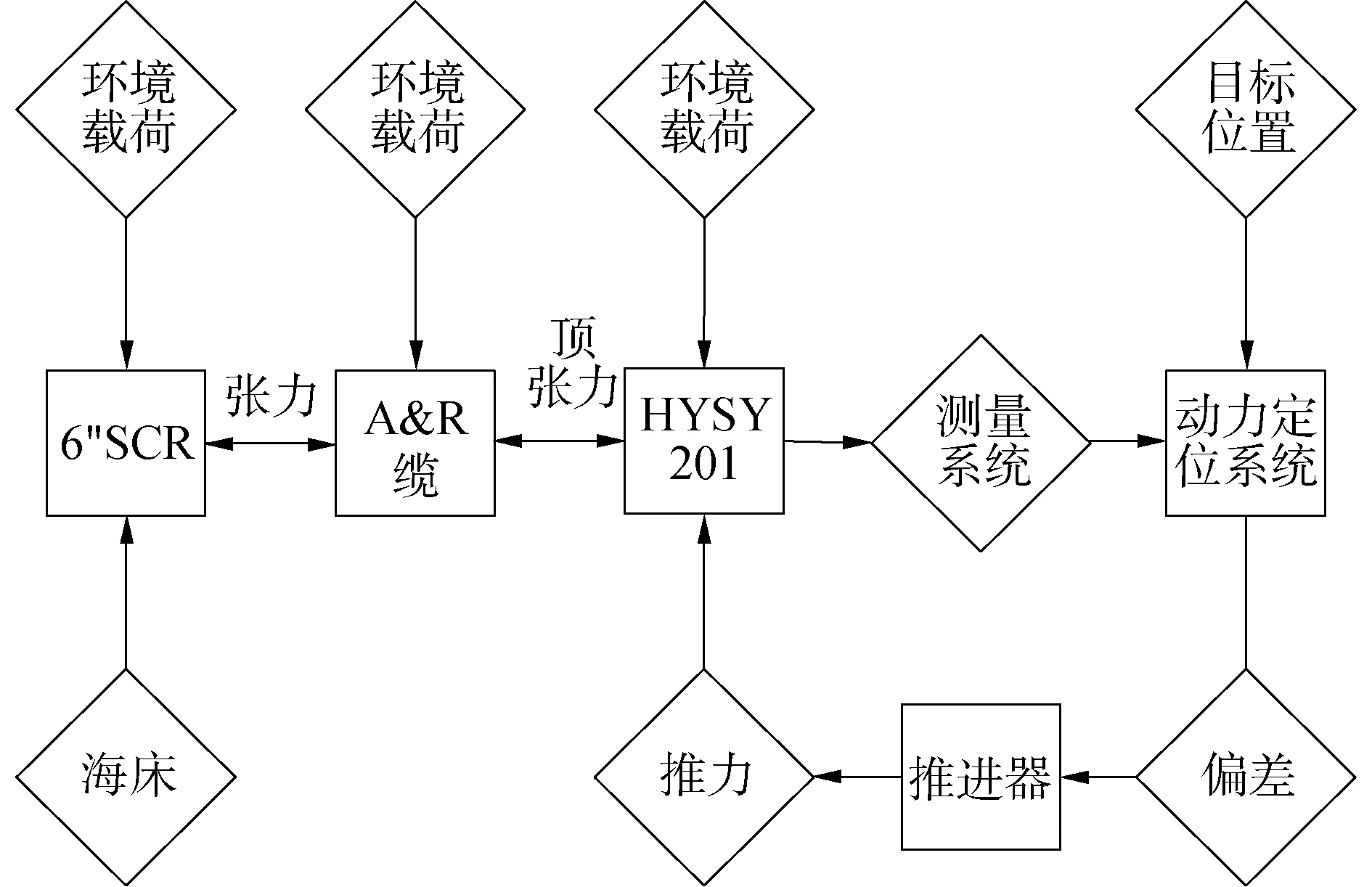
图3 仿真模型耦合系统Fig.3 The coupling system of simulation model

基于牛顿第二定律，安装作业船舶的六自由度运动方程可以表示为：

(1)

式中：M表示惯性矩；x(t)为作业船舶的运动；FR(t)为作业船舶强迫振动时所产生的辐射力；FH(t)为船舶偏离平衡位置而产生的静水回复力；FW(t)为作用于作业船舶上的波浪力；FE(t)为其他荷载：

FE(t)=Fc(t)+Fw(t)+Fd(t)+FT(t)

(2)

式中：Fc(t)表示流作用力；Fw(t)表示风作用力；Fd(t)表示动力定位的推进器系统的作用力；FT(t)表示舷侧顶张力。

2.1 船舶时域仿真理论

三维势流理论是将结构物周围流场中的流体视为均匀、不可压缩、无旋、无粘的流体，此时可用速度势的梯度来表示流场的速度。在势流理论中，微幅波问题可以转化为入射绕射和辐射问题，即在微幅波假定下的波浪流场中的速度势可用入射势、绕射势和辐射势来表示，即：

(3)

式中：φI为入射势；φD为绕射势；φRj为j个运动模态下的辐射势。

在理想流体状况下可用最基本的Laplace方程来求解速度势，在微幅波条件下，运用线性理论可以得到空间定常流动不可压缩流体速度势的基本控制方程和其定解条件：

控制方程：

▽2φ(x,y,z)=0

(4)

边界条件：

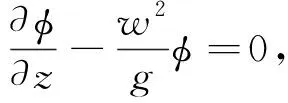
(5)

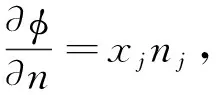
(6)

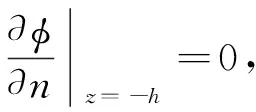
(7)

辐射条件：

(8)

式中：xj是在j个运动模态下的运动幅值；nj是在j个运动模态下的广义法向分量；k为辐射波的波数。根据入射势、绕射势、辐射势各自的定解条件最终求得速度势。

分别计算各个浪向下“海洋石油201”船垂荡、纵摇以及横摇下的运动幅值响应算子(response amplitude operaters, RAO)，计算结果与船模试验下的结果对比后基本吻合。具体计算结果见图4。

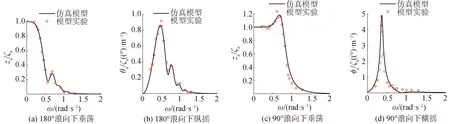
图4 各浪向下RAOFig.4 The RAO in each direction

2.2 钢悬链线立管与A&R缆动力学仿真原理

基于连续介质力学理论，采用有限元法建立钢悬链线立管与A&R缆相关理论模型。材料中微粒的运动可用拉格朗日方程表示，微小粒子在以基向量Ii定义的坐标系中运动如图5所示[13]。

粒子P在任意结构形态中都可通过位置矢量X来辨别，如图5所示，P在C0结构中的运动可表示为：

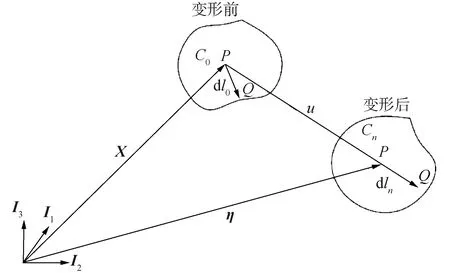
图5 微小粒子在空间中的运动Fig.5 The motion of small particles in space

η=η(X,t)

(9)

式中：η表示表示微粒经过时间t后所在的位置矢量；X表示粒子P在初始时的位置矢量；t表示运动的时长，位移矢量为：

η=X+u

(10)

拉格朗日公式中，应变可通过Green应变张量E来测量，以初始结构C0为例，应变张量可定义为：

dln2-dl02=dX·E·dX

(11)

式中：dl0表示PQ形变前长度；dln表示PQ形变后长度。

空间有限元系统模型的动态平衡一般可以表达为：

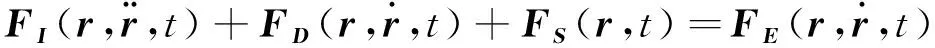
(12)

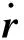
3 钢悬链线立管安装过程耦合仿真分析

3.1 作业仿真工况

3.1.1 环境参数

中国南海北部陵水17-2气田所在的海域实测取得环境参数如表3所示。风浪流方向为90°，垂直于“HYSY201”船中纵剖面。

表3 作业环境参数Table 3 Working environment parameters

3.1.2 立管安装阶段参数

为了方便对比分析将安装过程按照船舶距平台位置划分为5个作业阶段，具体安装阶段参数如表4所示。

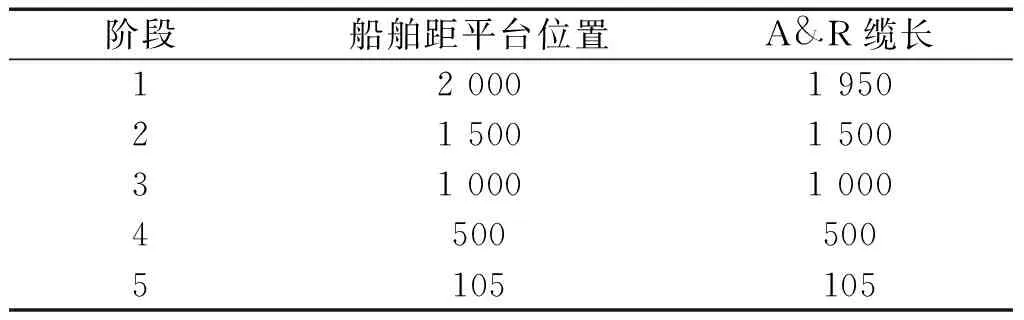
表4 安装阶段参数Table 4 Installation process parameters m

3.2 耦合仿真模型验证

为了验证模型建立的准确性，以第5阶段为例，将本文计算的结果与商用软件Orcaflex计算结果进行了对比，对比静态结果如图6、图7所示，可以看出钢悬链线立管与A&R缆的轴向拉力分布与弯矩分布几乎没有差异。为进一步验证模型准确性，本文模型所计算的A&R缆顶张力时历结果也需要与Orcaflex结果进行对比，考虑到Orcaflex没有动力定位模块，无法进行全耦合模型仿真，故将本文模型所得船舶六自由度作为Orcaflex输入参数，确保运动状态一致，顶张力时历对比结果如图8所示，对比结果基本一致，得以验证本文所用仿真模型准确性。

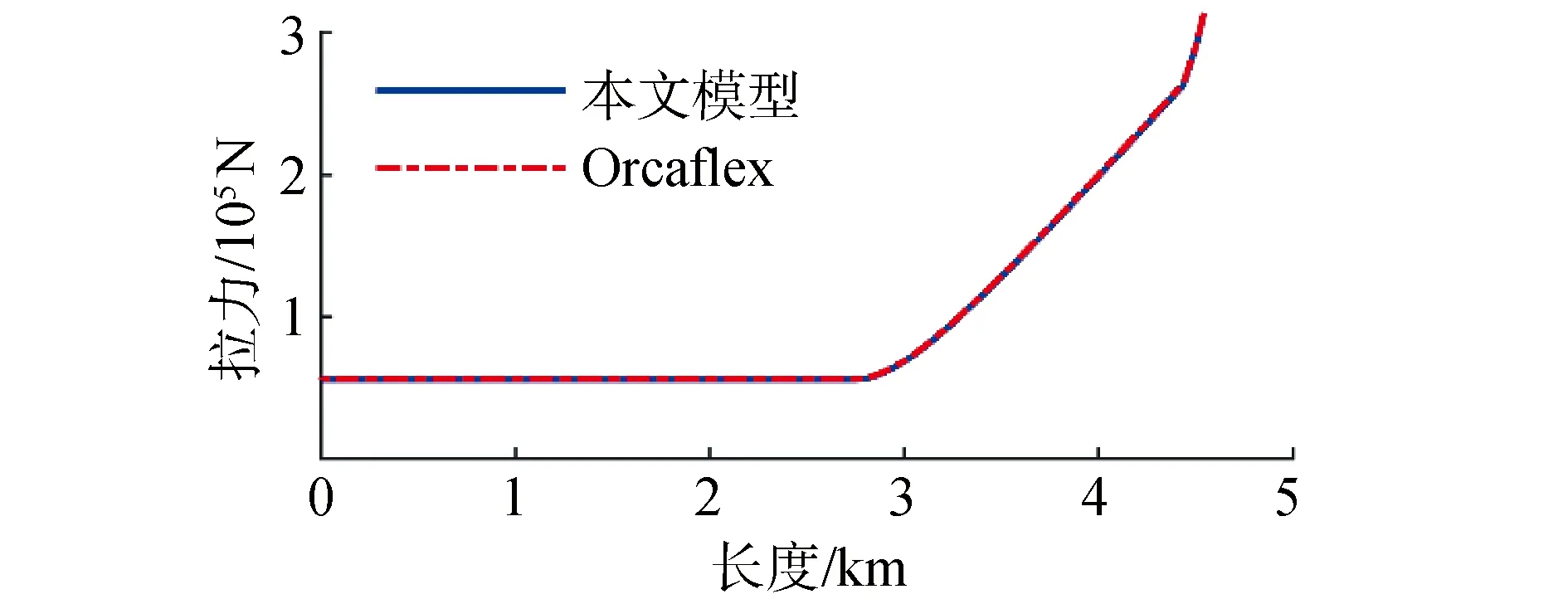
图6 钢悬链线立管与A&R缆拉力分布Fig.6 Tension distribution of SCR and A&R cables

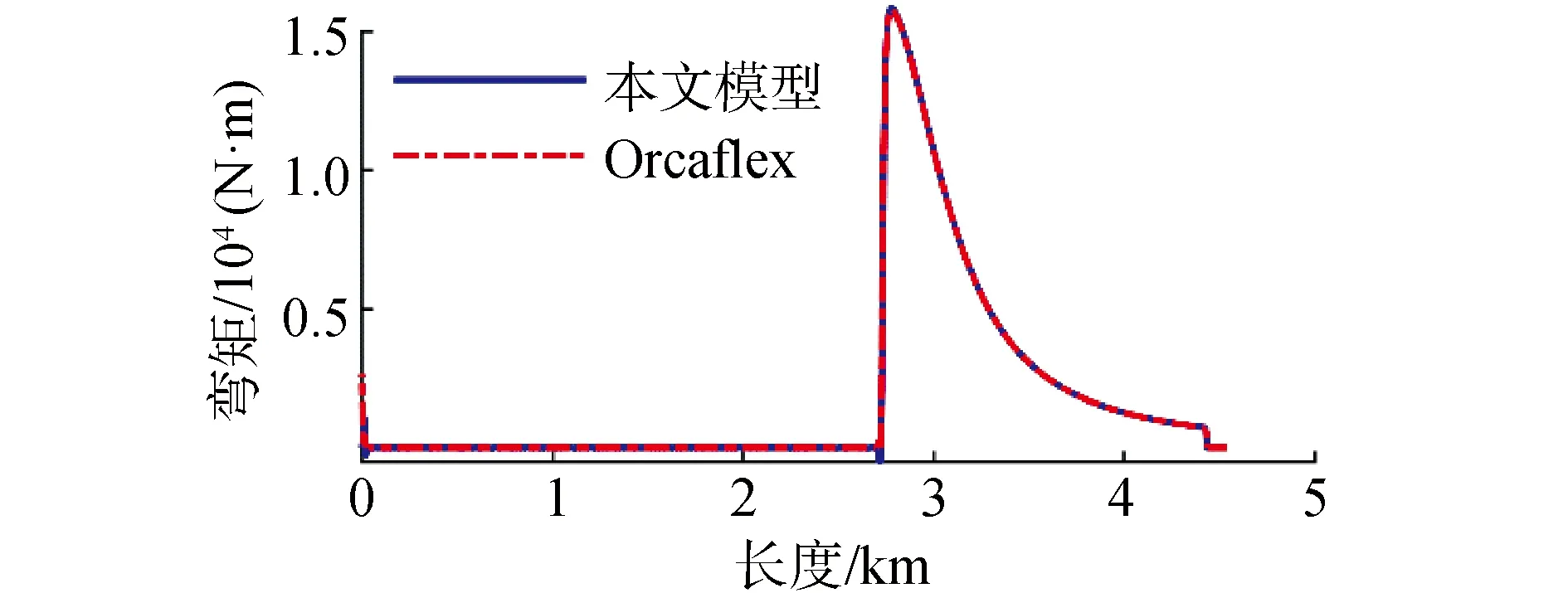
图7 钢悬链线立管与A&R缆弯矩分布Fig.7 Moment distribution of SCR and A&R cables

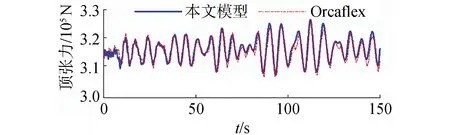
图8 顶张力时历对比Fig.8 The time histories of top tension

3.3 静力学计算结果

如图9所示为5个阶段下钢悬链线立管与A&R缆拉力分布，图中虚线部分为A&R缆各段拉力，实线部分为钢悬链线立管各段拉力。通过分析发现，由于舷侧位置受到A&R缆顶端向下作用力，各阶段下海床上的钢悬链线立管与A&R缆所受拉力基本一致。由于重力的作用，在悬垂段随着长度增加，钢悬链线立管与A&R缆所受拉力增加。由于A&R缆的质量系数比钢悬链线立管要高，在A&R缆与钢悬链线立管2段有着较为明显的单位长度上拉力增加程度的变化。着船舶向海洋平台靠近，钢悬链线立管悬垂长度增加，使用的A&R缆悬垂长度减少，随着整个悬垂段重力减小，张紧器所需要提供的张力也会越来越小。如表5所示为各阶段下顶张力A&R缆所受张力，最大值发生在初始阶段，最大值为835.5 kN，小于其承受极限400 t，在作业安全范围内。

图9 钢悬链线立管与A&R缆各段初始拉力Fig.9 Initial tension of SCR and A&R cable

表5 各阶段下顶张力Table 5 The top tension of each step

图10为5个阶段下钢悬链线立管与A&R缆弯矩分布，表6为各阶段下最大弯矩。其中分界线标志着钢悬链线立管与A&R缆的交点，在分界线左侧为钢悬链线立管段，右侧为A&R缆段，从图10中可以看到，由于海床整体平整，钢悬链线立管基本不会弯曲，在海床上的钢悬链线立管所受弯矩作用约为零。在海床上的钢悬链线立管由于末端固定，末端处钢悬链线立管局部曲率较大，会产生较大的弯矩。A&R缆弯曲刚度在仿真中忽略不计，所以A&R缆不会产生弯矩。对比分析弯矩图可知在钢悬链线立管在触地点位置附近会产生最大弯矩，因为此时钢悬链线立管曲率达到最大。随着船舶向平台位置靠近，由于钢悬链线立管触底点与末端固定点距离逐渐缩短，触地点附近曲率逐渐增大，因此管道最大弯矩会越来越大，且最大弯矩位置向管道末端逐渐靠拢。钢悬链线立管在最终阶段时弯矩极值最高，最大值为15.82 kN·m。对同一作业阶段下的弯矩变化而言，在触地点附近时钢悬链线立管曲率达到最大，此时钢悬链线立管弯矩达到最大，在钢悬链线立管悬垂段曲率变化率逐渐减小。钢悬链线立管弯矩变化越来越缓慢，在到达与A&R缆连接处会减少为0。在第一阶段时，由于此时钢悬链线立管未被提升，所以没有像其他4个阶段在触地点产生大弯矩，在这个作业状态时的最大弯矩发生在钢悬链线立管末端固定端，弯矩最大值为1075 N·m。

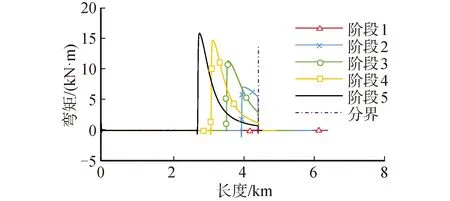
图10 钢悬链线立管与A&R缆各段所受弯矩Fig.10 The bending moment of SCR and A&R cable

表6 各阶段下最大弯矩Table 6 The maximum bending moment of each step

3.4 动力学计算结果

图11是初始阶段“海洋石油201”船六自由度运动的时历曲线。表7为初始阶段下船舶1 000 s内六自由度运动特征数据。如图11(a)～11(c)所示，由于船舶舷侧受到A&R缆与钢悬链线立管产生的拉力，所以船舶运动的初始6自由度状态并非为0，而是向舷侧系统所在位置发生了一定倾斜。

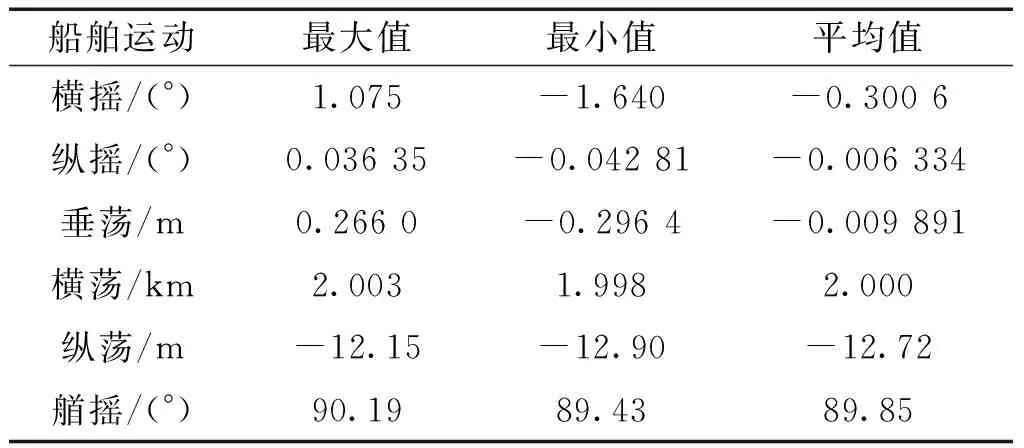
表7 船舶六自由度运动Table 7 The six degrees of freedom motion of ship

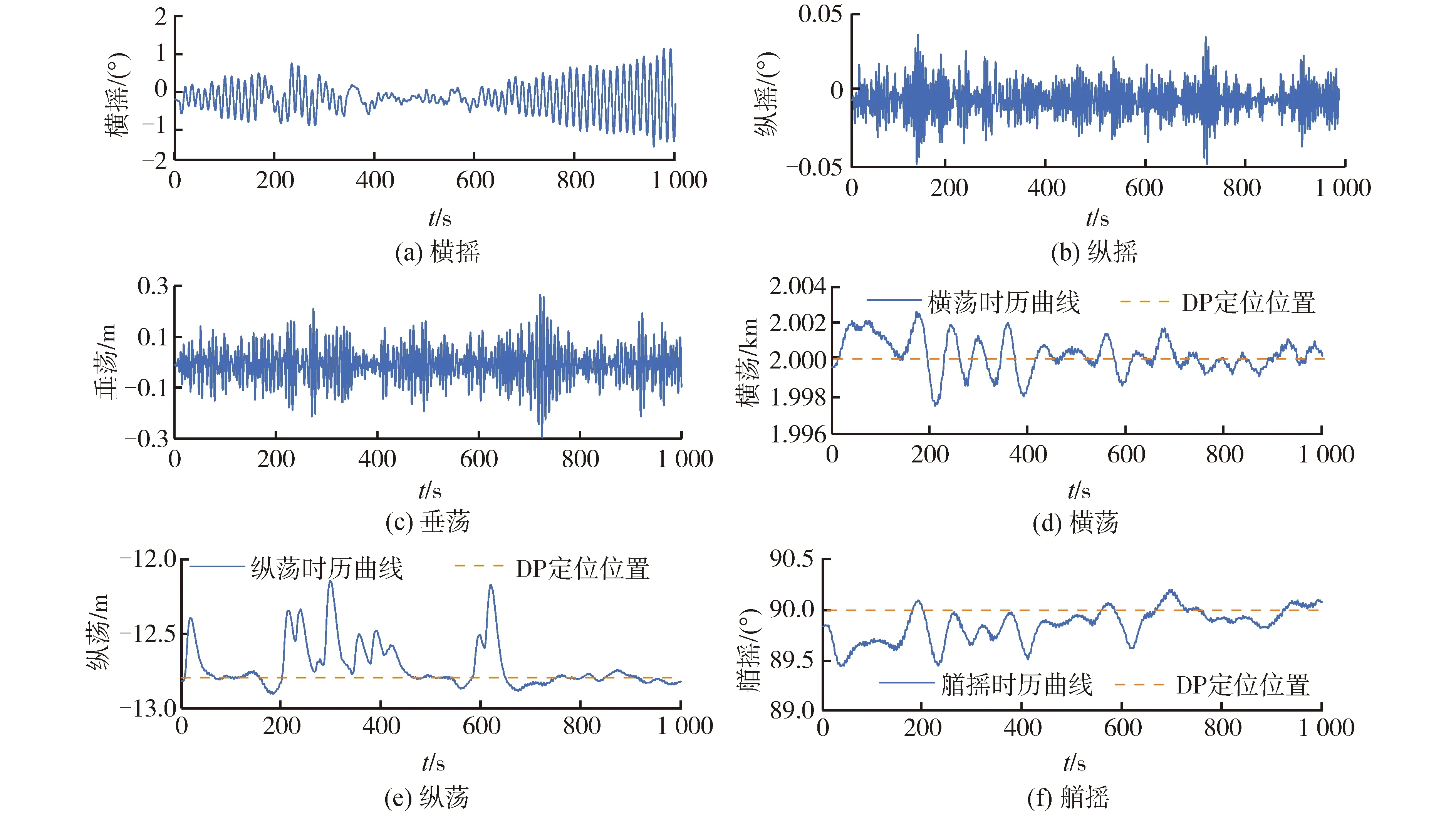
图11 六自由度运动时历曲线Fig.11 The time histories of six dements

船舶在横摇、纵摇以及垂荡3个自由度上的变化较为剧烈，由于风浪流垂直作用于船的中纵剖面，船舶横摇幅度较大，在2.715°范围内摇动，船舶纵摇、垂荡幅度总体较小，船舶纵摇在0.079 16°范围内摇动，船舶垂荡在0.562 4 m范围内运动，船舶在这3个自由度方向的运动符合海上船舶运动规律。船舶在横荡、纵荡以及艏摇3个自由度方向的运动由动力定位系统控制，在推进器推力作用下，船舶在这3个自由度上始终在目标位置附近进行运动，且运动较为平稳，同样由于风浪流作用，船舶横荡幅度较大，在5 m范围内运动，船舶纵荡与艏摇运动幅度较小，船舶纵荡在0.75 m范围内运动，船舶艏摇在0.76°范围内摇动。

图12为在钢悬链线立管舷侧安装不同阶段下，船舶舷侧位置最大顶张力以及钢悬链线立管最大弯矩变化曲线。如图12所示，在整个作业过程中，随着钢悬链线立管的逐渐提升，船舶所受的顶张力在逐渐减小，而钢悬链线立管所承受的最大弯矩则是在逐渐增加。最大顶张力发生在作业船舶距平台2 000 m位置处，最大弯矩则发生在钢悬链线立管安装最终位置处，与静力学仿真结论一致。

为了减小安装过程中的风险，对仿真工程中最大风险位置进行动态分析校核，图13为最大顶张力时历变化曲线，图14与图15分别为最大弯矩时历变化曲线与最大弯曲应力时历变化曲线。

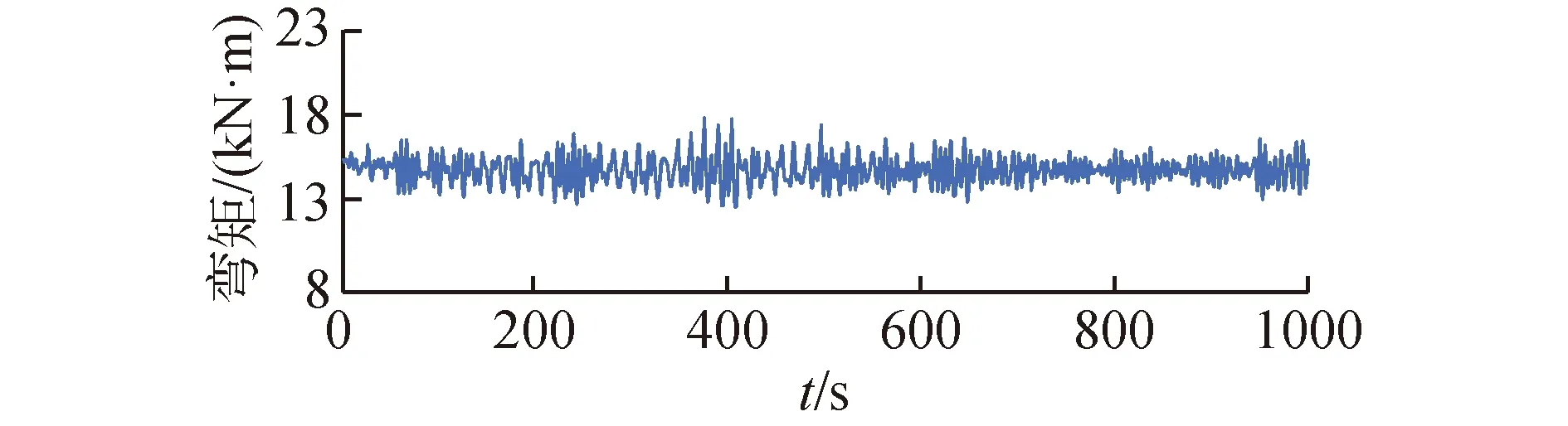
图14 弯矩时历曲线Fig.14 The time histories of bending moment

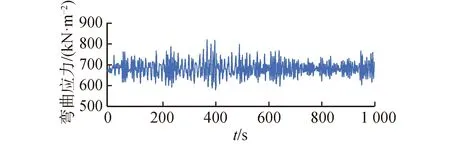
图15 弯曲应力时历曲线Fig.15 The time histories of bending stress

如图13～15所示，顶张力、弯矩和弯曲应力都随着船舶的运动发生着变化，表8为1 000 s时历内顶张力与弯矩特征值。在1 000 s内顶张力的最大值为930.6 kN，比静力计算结果增加11.4%，最小值为737.1 kN，比静力计算结果减小11.8%。1 000 s内顶张力的平均值为836 kN，与静力分析时的初始力基本一致。对比分析船舶运动时历曲线与顶张力时历曲线，可知船舶六自由度运动与顶张力变化有一定联系，船舶的运动对顶张力的变化影响非常大，在动力定位系统的影响下船舶不会偏移初始位置太多，A&R缆顶端位置在区间内运动，所以顶张力在193.5 kN波动。弯矩在时域内最大弯矩为17.96 kN·m，较静力计算值增加13.5%，时域内最小弯矩为12.80 kN·m，较静力计算值减小19.1%，时域内弯矩平均值为14.97 N·m。同顶张力一样，弯矩受船舶运动影响较大，由于动力定位系统的影响，A&R缆与钢悬链线立管悬垂段形态稳定在一定范围内，所以触地点弯矩在5.16 kN·m波动。在整个安装过程中钢悬链线立管承受的最大弯曲应力为81.82 kN/m2。