无人驾驶机器人多目标模糊操纵策略

齐东润， 陈 刚

(南京理工大学 机械工程学院， 南京 210094)

无人驾驶机器人(UDR)为自动驾驶的实现提供了新的思路.无人驾驶机器人是指无需对现有车辆进行底盘改装，可无损安装在驾驶室内，替代人类在危险和恶劣环境下进行驾驶操作的特种作业机器人.由于其良好的通用性，无人驾驶机器人可广泛应用于车辆测试试验、抢险救援等领域.目前，国内外主要有南京理工大学[1-3]、东南大学[4]、上海交通大学[5]、中国科学技术大学[6]，日本三重大学[7]、新西兰奥克兰大学[8-9]等高校对该技术进行了研究.

驾驶机器人对车辆进行操纵的过程可分为决策和控制两部分.文献[1]提出一种基于驾驶员行为模型的转向操纵策略，实现了对路径的跟踪.文献[2]提出一种基于纵向和横向误差的控制切换策略，提高了车速和路径的跟踪精度.文献[6]提出一种行驶辅助线的计算方法，实现了机器人驾驶车辆对路径的跟踪.文献[8]研究了纯跟踪、矢量跟踪等路径跟踪策略，并对其进行了对比.文献[9]提出一种利用前车的位置点生成平滑轨迹的方法，实现了机器人操纵车辆对前车的跟踪.文献[5]提出一种多方法融合策略，实现了对驾驶机器人车速跟踪误差原因的分析.通过上述文献研究可以发现，目前对驾驶机器人操纵策略的研究大多单独涉及纵向或横向，缺少对纵横向协同操纵策略的研究.因此，亟需在驾驶机器人纵向和横向操纵策略的基础上研究纵横向协同操纵策略.

文献[4]提出一种基于驾驶员经验和知识库的分层控制策略，实现了在驾驶试验周期内的准确速度跟踪.文献[7]研究了专业驾驶员的驾驶数据，并基于此提出一种控制策略，实现了对踏板的平稳操作和低油耗驾驶测试.上述文献的操纵策略制定方法使用查表或数据拟合的方式，这种方式只能应对相对固定的驾驶工况，在应对与之前经验不同的工况时表现不佳，且没有考虑车辆的横向动力学.文献[3]提出一种基于车辆性能自学习的转向机械手转角和力矩的求解策略，但没有考虑车辆转向时的稳定性.文献[10]提出一种预瞄式模型预测控制(MPC)路径跟踪策略，但没有考虑不同车速对转向的影响.文献[11]提出一种路径跟踪混合切换控制策略，根据车辆的车速切换不同的横向控制方法，提高了路径跟踪的准确性，但没有考虑路径曲率的影响.文献[12]利用广义预测控制实现了车辆的路径跟踪，增强了车辆抵抗干扰的能力，但缺乏对不同路径适应性以及与其他方法的对比验证.通过上述分析，目前关于驾驶策略的研究大多集中在单目标上，缺少对横向、纵向、速度、加速度等多目标同时考虑的操纵方法.多目标决策是对多个相互矛盾的目标进行科学、合理的选优后进行决策的理论和方法，已经广泛应用于各个领域[13-14].模糊决策中的模糊排序研究了对于有多种指标函数的方案如何用模糊理论给出一个排优次序的问题，是多目标决策问题的一种十分有效的解法.

基于以上分析，本文首先建立了驾驶机器人和被操纵试验车辆的动力学模型，提出了横摆角速度生成方法，并提出一种驾驶机器人多目标模糊操纵策略，综合考虑车辆横向和纵向状态，为实现驾驶机器人对车辆的平稳操纵提供了新的思路.

1 无人驾驶机器人系统结构与操纵模型

1.1 驾驶机器人的系统结构

驾驶机器人的整体结构如图1所示, 主要由驾驶机械腿、驾驶机械手、驱动电机组成.转向机械手与换挡机械手能够操纵各种车型的方向盘、变速杆、加速机械腿、制动机械腿，离合机械腿能够操纵各种车型的加速、制动、离合踏板，从而实现对车辆的控制.在自动挡车辆中不对离合机械腿进行控制.

图1 驾驶机器人整体结构Fig.1 Overall structure of driving robot

1.2 驱动电机模型

(1) 驾驶机械腿的驱动电机模型

无人驾驶机器人的驾驶机械腿采用永磁同步直线电机(PMSLM)作为驱动装置，驱动电机的动力学方程为

(1)

式中：vlm为直线电机线速度；Flme为直线电机电磁推力负载；Flml为直线电机推力负载；Flmd为直线电机阻尼负载；mlm为直线电机动子质量.

驾驶机械腿驱动电机矢量控制系统如图2所示，其中：SVPWM为空间矢量脉冲宽度调制.位置控制器根据目标位移和霍尔传感器传回的实际位移为速度环指定目标速度，速度控制器根据目标速度和实际速度为电流环指定目标电流值，电流控制器根据目标电流和实际电流以及磁极位置得出换相逻辑与定子电压，利用SVPWM和逆变器输出控制电流.

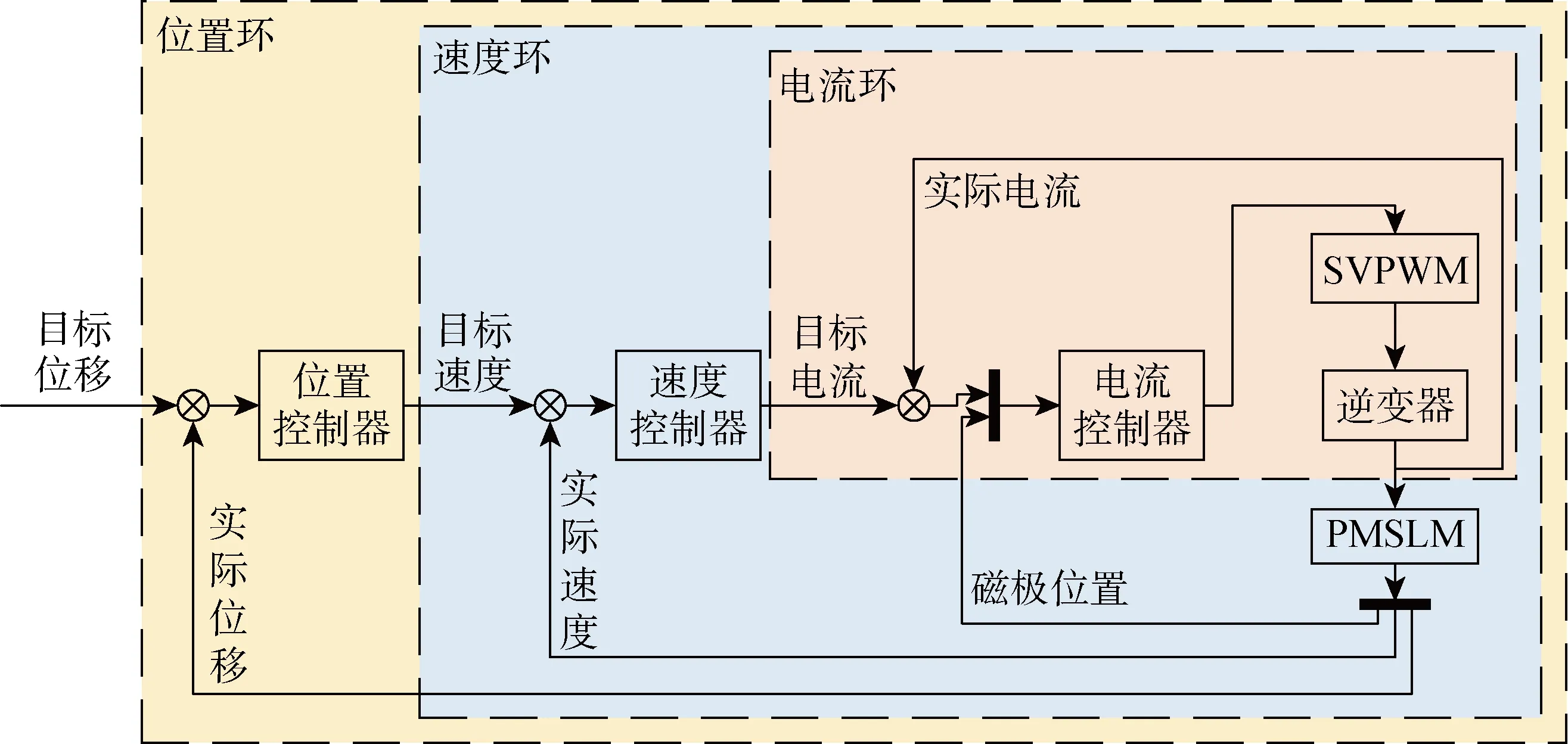
图2 驾驶机械腿驱动电机矢量控制系统结构图Fig.2 Structure diagram of vector control system for driving motor of mechanical leg

(2) 转向机械手的驱动电机模型

无人驾驶机器人的转向机械手采用无刷直流力矩电机作为驱动装置，驱动电机的动力学方程为

(2)

1.3 操纵机构动力学模型

(1) 转向机械手机构的动力学模型

转向机械手的结构简图如图3所示.

图3 转向机械手结构简图Fig.3 Schematic diagram of steering manipulator

忽略万向节的不等速现象，认为转向机械手为单自由度系统，其动力学方程为

(3)

式中：Jh为转向机械手等效转动惯量；i0为转向机械手减速器传动比；Mc为方向盘卡盘受到的负载力矩.

(2) 驾驶机械腿机构的动力学模型

驾驶机械腿的结构简图如图4所示.其中：A为驱动电机输出端；EF为踏板；vA、vC、vD、vE为驾驶机械腿各杆件连接点A、C、D、E的速度；vG、vH、vI、vJ为各杆件质心G、H、I、J的速度；ωAC、ωBD、ωDE、ωEF为各杆件AC、BD、DE、EF的角速度；sA为驱动电机输出端位移；α为踏板转角；FA为驱动电机输出端推力；M为踏板阻力矩.设各杆件质量均匀，质心均位于几何中心，由动能定理可得驾驶机械腿动力学模型为

图4 驾驶机械腿结构简图Fig.4 Schematic diagram of driving mechanical leg

(4)

式中：mAC、mBD、mDE、mEF为各杆件AC、BD、DE、EF的质量；JAC、JBD、JDE、JEF为各杆件AC、BD、DE、EF的转动惯量.

1.4 被操纵试验车辆的动力学模型

无人驾驶机器人操纵的试验车辆使用三自由度动力学模型：

(5)

用一阶惯性环节描述试验车辆驱动力Fth和加速机械腿位移sth、制动力Fxb和制动机械腿位移sxb的关系：

式中：Ta和Tb分别为驱动系统和制动系统的一阶惯性环节系数；ka和kb为比例系数；τ为时间常数；Fp为制动踏板力；kmc和kwc为制动主缸和制动轮缸的回位弹簧刚度；Amc和Awc为制动主缸和制动轮缸的活塞面积；kxb为制动常数.

被操纵试验车辆转向系统的动力学方程为

(9)

式中：Js为车辆转向系统等效转动惯量；is为转向系统传动比；kc为转向柱扭转刚度；MZ为回正力矩；ζ为轮胎拖距.

1.5 驾驶机器人与试验车辆集成动力学模型

结合式(3)～(9)，可得驾驶机器人与试验车辆的集成动力学模型为

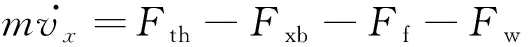
其中：s为拉普拉斯算子.

2 多目标模糊操纵策略

无人驾驶机器人对目标速度和目标横摆角速度进行跟踪即可完成试验车辆的驾驶任务，但车辆行驶在大曲率路径或较高车速时可能会产生较大的横向加速度，影响车辆的稳定性.减速可以使试验车辆侧向加速度减小，保证行驶的安全性，但减速时需考虑车辆的纵向加速度，过大的纵向加速度同样会影响车辆的稳定性.因此，需要对被操纵试验车辆的纵向操纵和横向操纵进行综合考虑.为实现驾驶机器人对车辆的平稳操纵，本文提出了基于多目标决策的无人驾驶机器人操纵策略.

2.1 横摆角速度生成

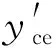
图5 试验车辆在坐标系中的位置Fig.5 Position of test vehicle in coordinate system

将预瞄距离lpr处预测的侧向偏移量进行泰勒二阶展开，可得：

(10)

(11)

式中：t′为时间间隔.

作为驾驶机器人进行路径跟踪的控制目标，预瞄点处的期望和预测侧向偏移量需相等，即

(12)

将式(12)、(13)代入式(11)，变形后得到期望横向加速度为

(13)

认为试验车辆质心侧偏角较小，则横摆角速度与横向加速度的关系为

(14)

将式(15)代入式(14)，得到期望横摆角速度为

(15)

在驾驶机器人对弯道进行跟踪时，需考虑由于路径曲率增加的横摆角速度可表示为

ωrc(t)=vxρ(t)

(16)

式中：ρ为路径曲率.由式(16)和(17)可得路径跟踪的总期望横摆角速度ωrd为

ωrd(t)=ωr(t)+ωrc(t)=

(17)

2.2 横纵协调操纵策略

使用驾驶机器人对车辆进行操纵，将上述横摆角速度作为目标横摆角速度进行跟踪即可完成对路径的跟踪，但可能造成车辆横向加速度过大.因此，将上述横摆角速度与试验要求车速作为参考值，使用多目标决策方法得到合理的目标横摆角速度与目标车速.

目标车速和目标横摆角速度的生成需要考虑试验车辆的性能约束.目标车速的生成需要考虑试验车辆的加速和制动性能，取纵向加速度的取值范围为 -5～2.5 m/s2[16]，则目标车速为

vx1=vx0+axΔt

(18)

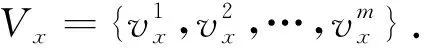
目标横摆角速度的生成需要考虑横向加速度的约束.考虑试验车辆的横向稳定性，取横向加速度的取值范围为 -4～4 m/s2，并假设质心侧偏角较小，目标横摆角速度为

(19)

式中：ωr1为下一时刻驾驶机器人对车辆进行操纵的目标横摆角速度；ay为横向加速度.当时间间隔Δt较小时，认为vx1与vx0相等，则有：

(20)

对可选方案集合中的方案进行排序和选优的判断标准为目标函数.选择驾驶机器人对车辆进行操纵时的车速误差、横摆角速度误差、纵向加速度、横向加速度4个指标对可选方案进行评价，因此需要建立这4个指标的目标函数.

(1) 车速误差：

ev=|vx1-vd|

(21)

(2) 横摆角速度误差：

eω=|ωr1-ωrd|

(22)

(3) 纵向加速度：

(23)

(4) 横向加速度：

ay=vx1ωr1

(24)

式中：vd为试验要求车速.由一个目标车速和一个目标横摆角速度进行组合即可得到一个方案，决策论域S是方案的集合，即S={s1,s2,…,si}，方案个数γ=m×n，且每个方案的目标函数值(ev,eω,ax,ay)都不同.

根据可选方案集合和目标函数即可建立驾驶机器人决策系统的特征量矩阵

(25)

根据评价指标的类型不同，需采用不同的隶属度计算公式将系统特征量矩阵转换为隶属度矩阵.隶属度计算公式为

“越大越优”型：

(26)

“越小越优”型：

(27)

目标区间型：

rij=

(28)

式中：λij为矩阵Λ中的元素；[q1,q2]为目标区间；λi,max为第i行中的元素最大值；λi,min为第i行中的元素最小值.

驾驶机器人操纵车辆的车速误差和横摆角速度误差为“越小越优”型，纵向加速度和横向加速度为目标区间型，分别使用式(28)和(29)将特征量矩阵转换为隶属度矩阵

(29)

表1 试验车辆横向与纵向加速度分级[17]

认为试验车辆的纵向与横向加速度为“好”或“一般”时，车辆较平稳.因此, 取纵向加速度的目标区间为[-2.5,1.2] m/s2，横向加速度的目标区间为[-3,3] m/s2.

由于各种评价指标的作用不同、地位不同，所以使用一个权重向量P来对各个评价指标的重要程度进行描述:

(30)

使用权重向量P可对驾驶机器人决策目标集合做出综合评判:

(31)

式中：h为目标函数的数量，本文中h=4.根据运算符⊕的不同定义，可得到不同的决策模型.

模型1：M(∧,∨)

uj=∨{(pi∧rij),1≤i≤h}

(32)

j=1,2,…,γ

模型2：M(·,∨)

bj=∨{(airij),1≤i≤h}

(33)

j=1,2,…,γ

模型3：M(∧,+)

uj=∑(pi∧rij)

(34)

j=1,2,…,γ

模型4：M(·,+)

uj=∑(pirij)

(35)

j=1,2,…,γ

驾驶机器人对车辆的操纵需要综合考虑多个指标.前3种模型的评判主要考虑最突出因素，其他因素对结果的影响不大.模型4对所有因素依照权重大小均匀考虑，适用于考虑所有因素的情况.因此，本文采用模型4对驾驶机器人操纵方案进行评判.最终, 向量U中值最大的分量所对应的方案即为最佳方案，该方案对应的车速和横摆角速度即为驾驶机器人操纵车辆的目标车速和目标横摆角速度.

3 仿真试验与验证

UDR多目标模糊操纵策略结构如图6所示.为了验证所提策略在驾驶机器人操纵车辆时的有效性，将驾驶机器人安装在试验车辆上，进行双移线仿真试验，试验车速为50 km/h，驾驶机器人安装图如图7所示，试验关键性能参数如表2所示.人类驾驶员操纵车辆在交通部公路交通试验场进行了双移线试验[18].试验由熟练驾驶员驾驶桑塔纳某型号轿车进行，两名试验员随车实时采集测试数据.横向加速度、横摆角速度和车辆位置信息由CDY-3车辆动态测试仪进行测量，纵向车速由OES-II非接触速度传感器测量，质心侧偏角可以间接测量.

图6 UDR多目标模糊操纵策略结构图Fig.6 Structure diagram of multi-object fuzzy control strategy for UDR

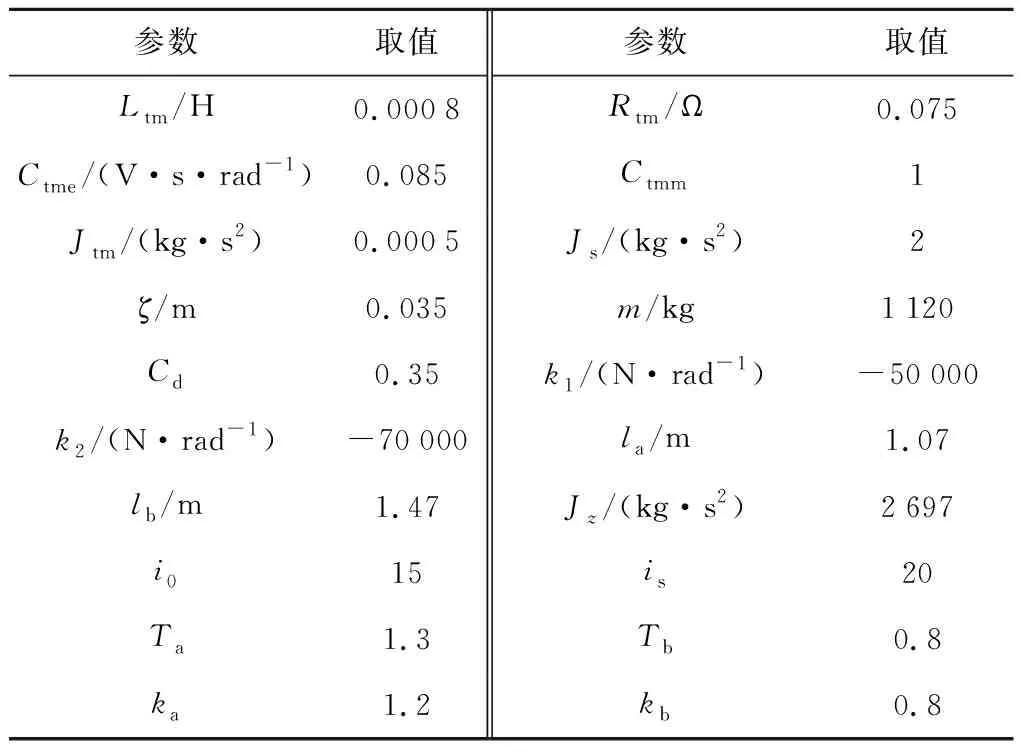
表2 试验车辆关键参数Tab.2 Key parameters of test vehicle

图7 驾驶机器人安装图Fig.7 Installation of driving robot

驾驶机器人操纵车辆与人类驾驶员驾驶车辆进行双移线试验的对比如图8所示，驾驶机器人操纵策略包括提出策略和无协同策略[1].图中：ey为路径跟踪误差.由图8(a)可知，仿真试验与实车试验的曲线变化趋势吻合，能够准确地跟踪目标路径，表明了提出策略的有效性.由图8(b)可知， 人类驾驶员存在反应滞后、跟踪误差较大等问题，而所提策略能够更加精确地跟踪目标路径，将误差控制在 0.2 m 以内[19]，平均绝对误差(MAE)为 0.014 9 m，在四处转弯处也能够很好地控制跟踪误差.由图8(c)可知，在弯道处横向加速度超过了阈值，所提策略对车速进行了调整，从而降低了横向加速度，保证车辆行驶的平稳性；无协同策略虽然也能将误差控制在0.2 m以内，但MAE值为 0.038 3 m，大于所提策略，且没有考虑横向加速度对车辆平稳性的影响.

图8 双移线工况试验结果对比Fig.8 Comparison of test results in double lane-change condition

为了进一步验证所提出无人驾驶机器人操纵策略的有效性，采取如图9(a)所示的目标路径进行仿真试验，并与其他操纵策略进行对比，目标车速为48 km/h.该路径同时包含大曲率路径与一般曲率路径，因此可以验证策略的有效性.试验分别采用所提策略、无协同操纵策略与单目标操纵策略.无协同操纵策略未考虑驾驶机器人横纵协同操纵.单目标操纵策略仅考虑横向加速度，未考虑纵向加速度，使用单一的制动方式减小横向加速度，如下式所示：

(36)

式中：[ay，max]为最大安全横向加速度；na为安全系数.

由图9(a)可知，3种策略均可对路径进行较准确的跟踪.图9(e)为由本文策略得出的目标横摆角速度和跟踪结果.由图9(e)可知，控制机构可以对横摆角速度进行准确的跟踪.由图9(b)可知，在该工况下有6处横向加速度超过阈值，无协同策略没有对横向加速度进行控制，其余两种策略在这6处均进行了减速操作，相比于无协同策略将横向加速度超过阈值的时间缩短了80%以上，但由于单目标策略未考虑纵向加速度，也未考虑车辆的实际性能约束，在操纵时出现了较大的纵向加速度数值，最大加速度为10.77 m/s2，最大减速度为35.45 m/s2，如图9(d)所示.该策略仅通过降低车速的方法控制横向加速度，导致车速误差较大，如图9(c)所示.而所提策略同时考虑了横纵向加速度与车速误差，在减速的同时保证了纵向加速度的合理性，最大加速度为1.33 m/s2，最大减速度为3.05 m/s2，且降低了车速误差，因此可以实现驾驶机器人对车辆的平稳操纵，从而验证了所提策略的有效性.

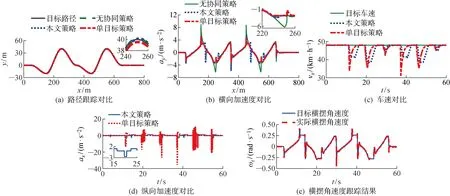
图9 不同曲率路径的路径跟踪试验结果对比Fig.9 Comparison of tracking test results in different curvature paths

双移线和多曲率工况路径跟踪的统计分析如表3所示.通过计算MAE对行驶轨迹进行量化，其中：eey为路径跟踪误差的平均绝对误差.由表3可知，本文策略在两种工况下都能够较好地跟踪目标路径，跟踪误差较小，说明了所提策略的跟踪精度性能具有一定的稳健性.

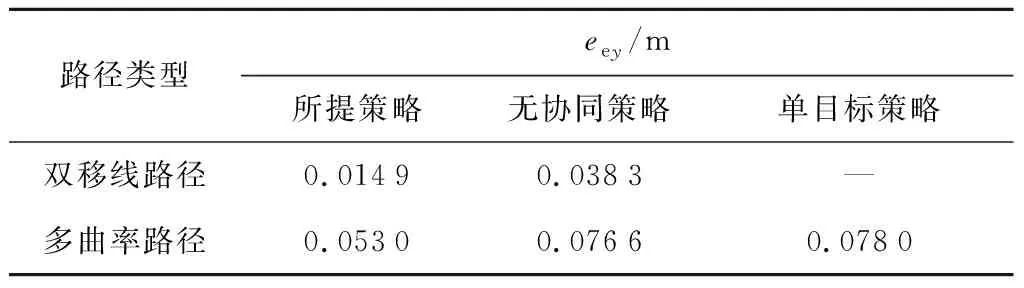
表3 路径跟踪误差的MAETab.3 MAE of path tracking error

本文的多曲率路径由4段不同曲率的路径拼接而成，每种曲率的路径重复两次，因此可以用来验证所提策略在控制车辆加速度方面的稳健性， 如表4所示.由表4可知，所提策略在4种不同曲率路径下都能够对车辆的横向、纵向加速度进行控制，证明了所提策略对不同曲率路径的稳健性.

表4 车辆加速度分段最大值Tab.4 Segmental maximum accelerations of vehicle

4 结论

(1) 提出了基于多目标模糊决策的驾驶机器人操纵策略.建立了驾驶机器人与试验车辆的集成动力学模型，设计了横摆角速度生成方法和无人驾驶机器人横纵协调操纵调整策略，并进行了试验与仿真验证.

(2) 驾驶机器人操纵车辆的双移线路径跟踪试验表明了，横摆角速度生成方法能够控制车辆平滑地进行路径跟踪，并将误差控制在±0.2 m以内.对比试验表明了，当试验车辆横向加速度过大时，所提策略能够在多目标约束下有效减小横向加速度，保持车辆平稳.

多目标模糊决策方法只能在一定步长的离散值方案中选择驾驶机器人操纵的目标车速和目标横摆角速度，当试验要求车速或横摆角速度的变化量小于步长时，跟踪精度会有所降低.今后将考虑使用强化学习等其他智能方法实现在一定范围内对决策方案的连续取值，提高实验要求车速或路径在小范围内变化时的跟踪精度.本文提出的策略没有考虑其他车辆、障碍物、行人等路况环境参量，后续的工作将把这些参量加入研究范围.