基于Mindlin 理论的新型模式转换超声振动系统设计与研究

张宁宁，朱 佳，袁金霖

（ 渭南师范学院物理与电气工程学院，陕西渭南 714099 ）

超声辅助加工被广泛用于难加工材料如高性能合金、复合材料、硬脆材料等的高效精密加工[1]。超声辅助加工的核心部件是超声变幅杆，直接决定加工性能。 目前国内外研究者对各种常规形状超声变幅杆研究比较成熟。 若加工工具的质量较小时可忽略其影响，直接进行变幅杆设计；当加工工具质量较大时，则需对超声变幅杆和工具杆进行一体化设计[2]。 杯型工具的尺寸和质量较大，其固有振动频率、振动模态等很难满足超声加工要求，应把杯型工具看作是超声振动系统的非谐振动单元进行整体设计[3-7]。 文献[8]对超声珩磨声学系统中的圆盘进行研究。 文献[9]研究了用于超声焊接的超声杯型工具。 文献[10-11]基于纵振理论和薄圆盘振动理论对超声变幅杆与杯型工具进行设计研究。 以上文献所设计的都是单一变幅杆与圆盘、杯型工具组成的振动系统。 而实际应用不仅要求变幅杆的放大系数较大，还需弯曲劲度高、稳定性好，因此复合型变幅杆多被采用。 另外，由于薄扳适用范围小，特别在高频大功率声条件下需用厚板，Mindlin 厚板理论相比于薄板理论的计算精度更高。

本文设计了一种新型模式转换超声振动系统，通过分析各段的振动模态，分别建立部分的位移和应力函数， 根据连接处的连续条件和边界条件，推导出新型模式转换超声振动系统的频率方程，根据频率方程并利用计算机编程实现了新型振动系统的设计；对所设计的振动系统进行数值计算和有限元模态和谐响应分析；研究了各几何参量对振动系统谐振频率的影响规律。 结果表明：理论计算、有限元分析、实验测试结果基本一致；新型振动系统的谐振频率随着圆盘厚度的增加而增大，变幅杆面积比不变时随着大小端半径的增加而增加，随着变幅杆各段长度、圆管段高、内径的增大而减小。 研究结果还表明：所设计的振动系统结构合理、振动效果良好，为超声辅助加工特别是硬脆材料高精度曲面加工技术提供了一种新型超声振动系统以及频率调试依据。

1 新型超声振动系统数学模型

为了获得更高的频率和功率，本文设计了一种新型模式转换超声振动系统， 具体结构如图1 所示，从左到右分为三部分，依次为：第一部分为三段复合变幅杆，其中第一段复合变幅杆的大端圆柱形半径为R1、长度为L1，第二段过渡段圆锥形杆长度为L2，第三段小端圆柱杆半径为R2、长度为L3；第二部分为厚圆盘，其半径为R3、长度为L4；第三部分为大尺寸圆管，其内半径为R4、长度为L5。研究的关键是，对复合变幅杆与圆盘、圆管三种结构组成超声振动系统进行谐振设计。

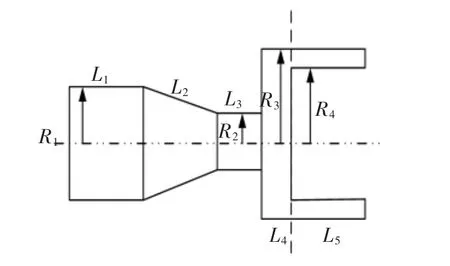
图1 新型模式转换超声振动系统的结构图

2 新型模式超声振动系统的频率方程

2.1 各段位移与力

2.1.1 中厚圆盘的位移和力

由考虑横向剪切变形和转动惯量影响的Mindlin 厚板理论可知，零节径轴对称弯振圆盘的横向位移ϖ（r）、ψr转角、Qr剪力、Mr弯矩分别为[12-13]：

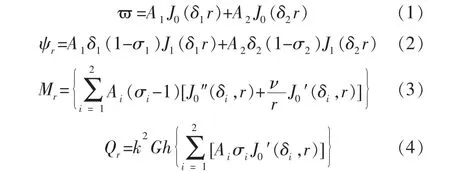
式中：J0（δir）为零阶贝塞尔函数；Y0（δir）为零阶诺伊曼函数；J1（δir）为一阶贝塞尔函数；Y1（δir）为一阶诺伊曼函数；A1、A2均为由边界条件决定的待定常数。

另有：

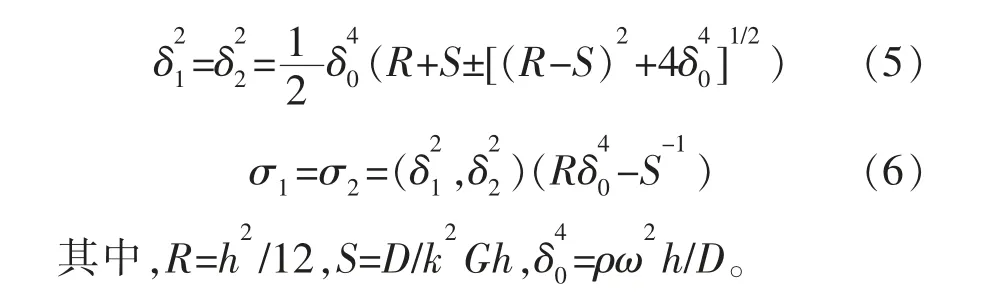
式中：D=Eh3/12 （1-ν2）；k2=π/12；ρ，ω，D 分别为密度、角频率、弯曲刚度常数；R、S 为转动惯量和横向剪切变形的影响；ν 为泊松比。

2.1.2 圆锥形复合变幅杆各段的位移与应力

根据波的纵振动理论可得大段圆柱段纵向振动变幅杆的位移函数和应变函数分别为：

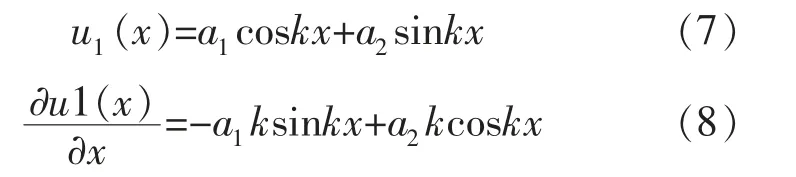
圆锥形纵向振动变幅杆的位移函数和应变函数分别为：

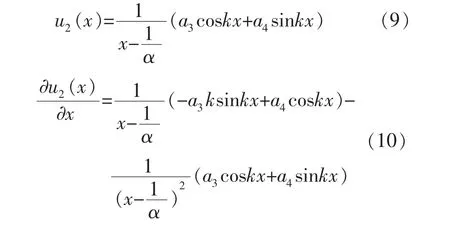
小段圆柱形纵向振动变幅杆的位移函数和应变函数分别为：

2.1.3 圆管段的位移和应力

圆管段的位移函数和应变函数分别为：

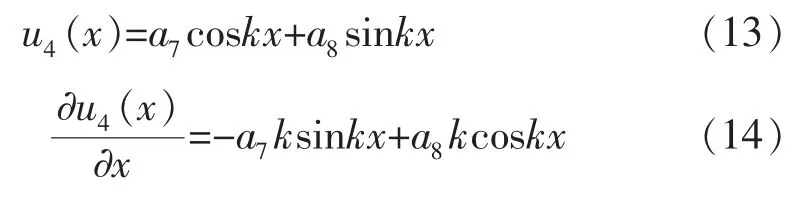
2.2 新型振动系统的频率方程

对于全波长超声振动系统，复合变幅杆大段圆柱段的左端面位移振幅最大，圆管段的右端面为自由状态，存在若干边界条件。

变幅杆的左端与传振杆相连， 位移振幅最大，即有位移的导数为零的边界条件：

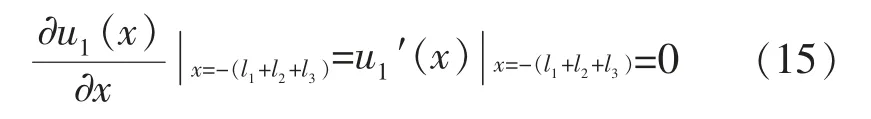
对于作一维纵向振动的变幅杆各部分的位移和力连续，即有边界条件：

变幅杆右端与圆盘连接， 满足力和位移耦合，即有位移与力相等的边界条件：

圆管段右端面是自由状态，应变为零，因此有边界条件：

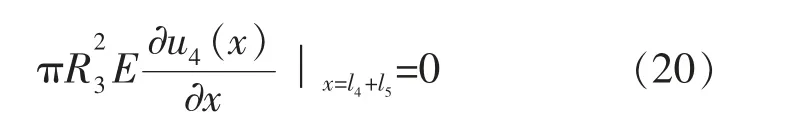
式（15）～式（20）是超声振动系统的谐振数学模型， 关于待定常数a1、a2、a3、a4、a5、a6、a7、a8、A1、A2的十阶齐次线性方程组， 要使方程组有非零解，就得满足系数行列式为零，即式（21）。

式（21）为新型模式转换超声振动系统的谐振频率方程，其中包含谐振频率和各组成部分的材料参数和尺寸参数。 如果各组成部分的材料参数和尺寸参数已知，则由式（21）可确定振动系统的谐振频率；反之，如果已知振动系统的谐振频率和材料参数以及其他尺寸参数，也可由式（21）解得振动系统的未知设计参数，可完成对新型模式转换超声振动系统的设计。

3 设计结果及振动性能分析

3.1 设计结果

超声振动系统采用45 钢，其材料参数为：密度ρ=7.8×103kg/m3、泊松比ν=0.28、弹性模量E=2.16×1011N/m2、剪切模量G=8.4×1010N/m2。 具体几何参数为：变幅杆大端直径D1=54 mm、长度L1=30 mm，小端直径D2=30 mm、L3=38 mm； 圆盘半径R3＝39 mm、长度L4＝16 mm；圆管段的内半径R4＝35 mm、外半径R3＝40 mm、长度为L5＝30 mm。 若所设计振动系统的谐振频率f＝30 kHz， 则波速c＝5200 m/s。将上述已知参数代入式（21），用Matlab 编程经数值计算可得频率方程解的误差Δ 与L3的关系见图2。可知，在L3为6～66 mm 搜索范围内，满足频率方程解误差Δ=0 条件的只有一个，即可得出L3＝30 mm。

图2 频率方程误差与L3 的关系图

3.2 有限元分析

3.2.1 模态分析

根据所设计新型模式转换超声振动系统的几何参数， 本文基于ANSYS14.0 建立了三维模型，采用8 节点的SOLID45 单元智能自由划分网格，采用Block Lanczo 模态提取方法， 取频率提取范围为1～50 kHz，以此进行有限元模态分析。 从各模态的分析中可得出与设计频率30 kHz 最接近的谐振频率为29.029 kHz 的纵振模态，经计算得出与设计频率的误差为3.23%。 由图3 所示振动系统谐振位移分布情况可看出，系统振动模态为纵弯纵径耦合形式，其余频率均为复杂振型。 通过圆管段所有节点的纵向位移图4 和横向位移图5 比较，可得纵向和径向的位移比约为3.28 ， 故圆管段以纵向振动为主。由图6 所示新型超声振动系统轴线的纵向相对位移分布图可知，经过超声振动系统输出端位移被放大一倍多。

图3 新型超声振动系统的谐振位移分布图

图4 圆筒纵向相对位移分布图

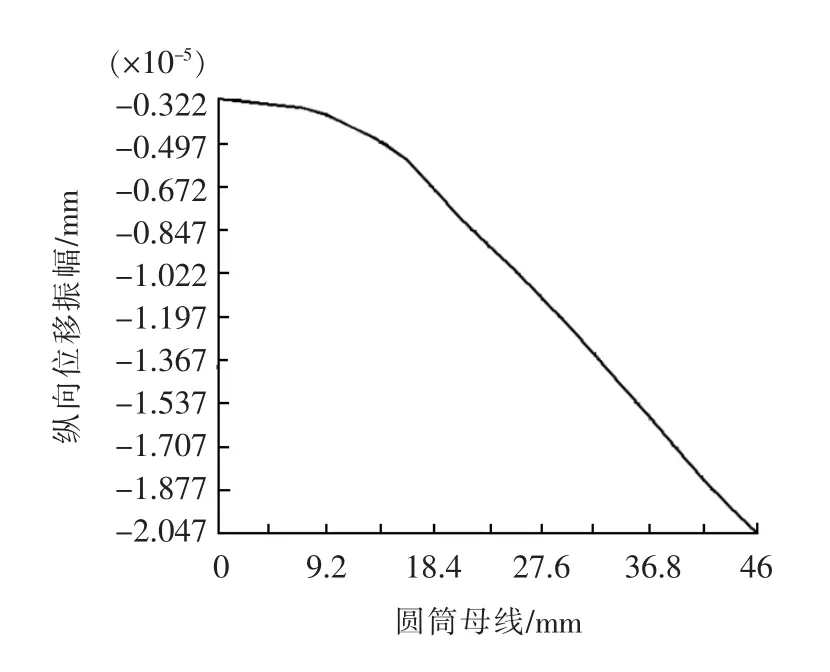
图5 圆筒径向相对位移分布图

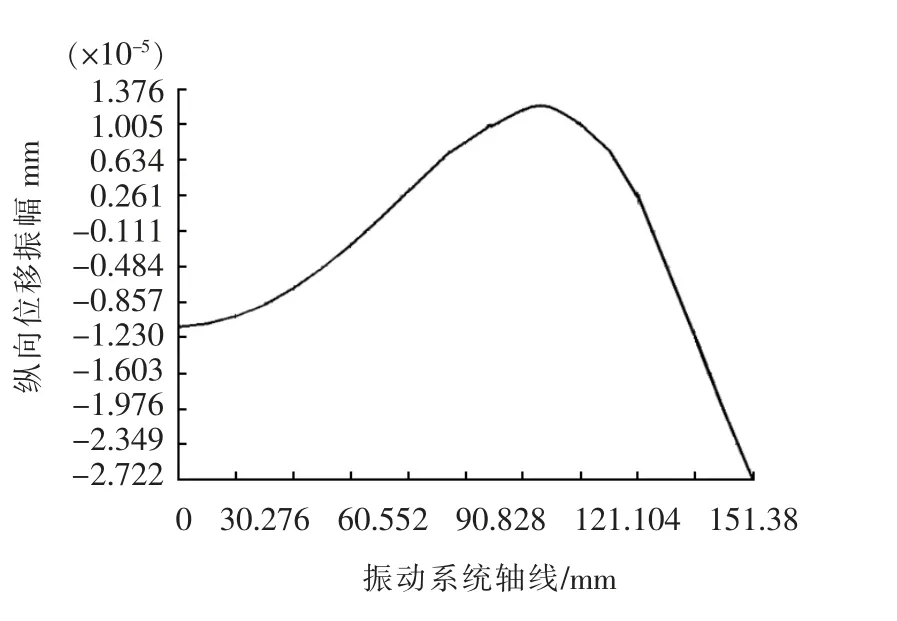
图6 新型超声振动系统的轴线纵向相对位移分布图

3.2.2 谐响应分析

为进一步研究新型模式转换超声振动系统的动力学特性，在模态分析的基础上对其进行谐响应分析。将谐响应分析的激励频率选取为f=29.029、频率附近的频率区间设置为28.919～29.119 kHz，以此进行求解。 由图7 所示，新型超声振动系统的位移-频率响应曲线可得，振动系统输出端的位移振幅为8.711 μm，通过计算可得新型超声振动系统的振幅放大系数Mp=8.711/6≈1.45，这表明波的振幅被进一步放大。

图7 新型超声振动系统的位移-频率响应曲线图

3.3 振动特性研究

用数值计算和有限元仿真对新型超声振动系统的变幅杆各段长度以及圆管段高度、 圆盘厚度、圆管段内径等几何参数对系统谐振频率的影响规律进行了研究，结果见表1～表3。 在各表中，f0是薄板理论计算结果、f1是理论计算结果、f2是有限元仿真结果、Δf1是薄板理论计算结果与有限元仿真结果的百分误差、Δf2是理论计算结果与有限元仿真结果的百分误差。

3.3.1 圆管高和内径对超声振动系统谐振频率的影响

由表1 可知，在圆盘厚度、内径不变的情况下，将圆管段高度由24 mm 增大到30 mm 的过程中，超声振动系统谐振频率理论计算值与仿真值误差较小（在5%以内）且逐渐减小，其变化趋势一致。 同时可得在圆盘厚、圆管段高不变的条件下，仿真结果与理论计算值的变化规律相同，谐振频率随着内径的增大而降低，内径每增大1 mm，其谐振频率基本在200～300 Hz 的范围内减小。

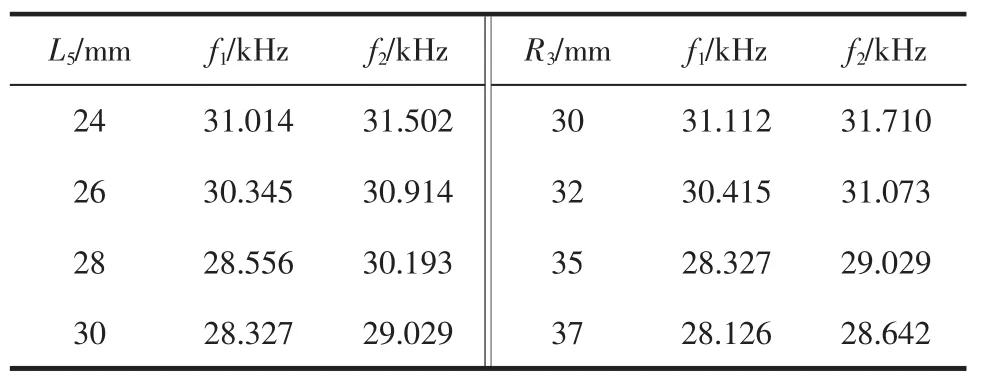
表1 振动系统谐振频率随着杯高和内径变化

3.3.2 圆盘厚对超声振动系统谐振频率的影响

由表2 可知，在圆管段高度、内径不变的条件下，仿真结果与厚板理论计算值误差较小，但薄板理论计算结果误差较大， 表明本文理论的正确性，而且可看出超声振动系统谐振频率随着底厚的增加而增加，每增大2 mm，其谐振频率大约增加200～300 Hz。

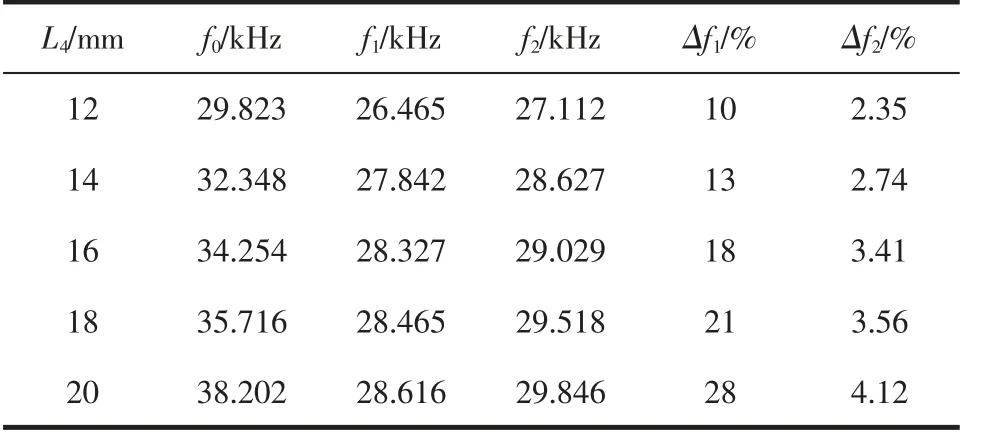
表2 振动系统谐振频率随着杯厚变化

3.3.3 变幅杆各段长度对超声振动系统谐振频率的影响

由表3 可知， 仿真结果与理论计算值基本一致，结果表明在圆盘厚、圆管段高以及半径不变的条件下，超声振动系统的谐振频率随着变幅杆各段的增大而降低，L1每增大2 mm，其谐振频率减小约为250～350 Hz，L2每增大2 mm，其谐振频率减小范围为300～400 Hz，L3每增大2 mm，其谐振频率减小范围为500～600 Hz，对比可得变幅杆各段长度对系统谐振频率的影响不同， 其大小顺序为：L3＞L2＞L1；当变幅杆大小端面积比不变时，系统的谐振频率随变幅杆大小端半径的增加而增加。

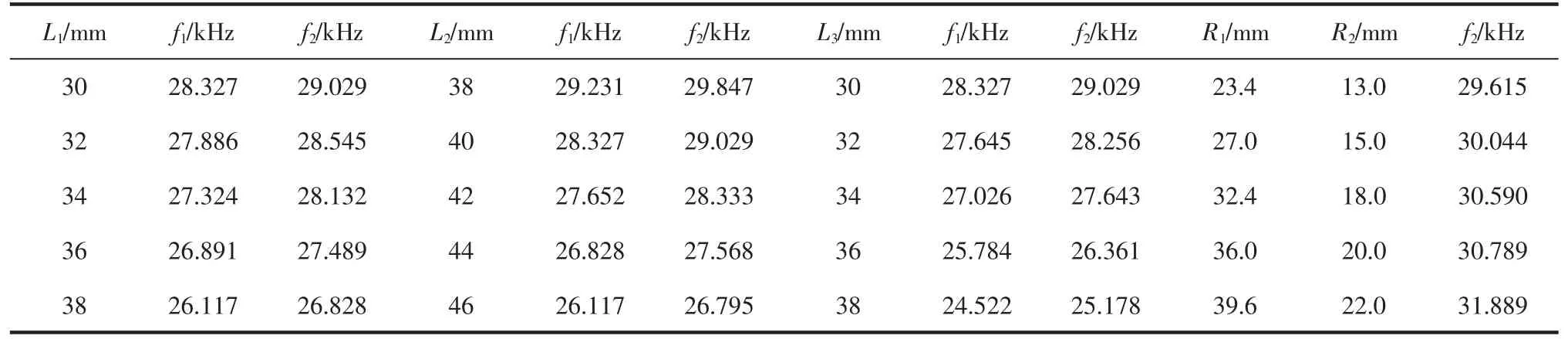
表3 振动系统谐振频率随着变幅杆各段长度、半径变化

4 实验

按照以上设计尺寸对振动系统进行加工，由PV70A 阻抗分析仪可得出超声振动系统实验测试的谐振频率大约为29 828 Hz，其结果与ANSYS 模态分析结果及理论计算结果基本一致。 同时，振动系统的导纳圆圆度较好，电导曲线正常；机械品质因数较高，其电声转化效率也高，这表明以上建模和设计是合理的。 出现误差的主要原因有：①各连接处采用螺纹连接，导致接触不够紧密，造成一定的能量损失； ②实际进行装配时预留了一定的空隙， 而仿真时则没有预留； ③在有限元分析时，网格尺寸对系统的谐振频率有影响； ④在理论分析时，与实际加工的材料参数不完全一致，也会造成一定误差。

5 结论

对一种新型模式转换超声振动系统进行一体化设计， 并对设计的超声系统的振动特性进行研究，得到以下结论：

（1）根据波传播理论建立新型模式转换超声振动系统的数学模型，在对超声系统各段振型分析基础上， 基于波的纵振动理论和Mindlin 厚板弯曲振动理论建立了各段的位移和应力函数，根据连接处的连续性条件和边界条件，得到新型模式转换振动系统的频率方程。

（2）对所设计的新型振动系统进行有限元模态分析可得其振动形式是“纵-弯-纵”，在圆管形段虽存在一定的横向振动，但经过计算可得主要振动形式是纵向振动；有限元谐响应分析可得经过纵弯纵模式转换系统后振幅得到进一步放大。

（3）新型模式转换超声振动系统谐振频率的设计结果与有限元分析及测试结果误差较小， 在5%以内，验证了所建系统数模型和振动频率方程的正确性。 通过进一步研究可知当其他参数条件不变时，随变幅杆各段长度和圆管段的长度、圆盘的半径和圆管段的内半径的增加振动系统的谐振频率减小；随圆盘厚度和变幅杆大小段半径的增加系统的谐振频率增大。 因此在实际工程应用中，可由以上规律通过调整振动系统各段尺寸参数实现对新型模式转换超声振动系统谐振频率的调整。