混联驱动三维椭圆振动辅助切削系统压电迟滞建模与补偿

卢明明，付喜锋，周家康，宋盾兰，杜永盛

（ 长春工业大学机电工程学院，吉林省微纳与超精密制造重点实验室，吉林长春 130012 ）

近年来，椭圆振动辅助切削技术被广泛应用于国防、航天航空等亟需超精密制造技术的领域。 从20 世纪80 年代专家学者基于一维振动切削的基础提出的椭圆振动切削技术（2D-EVC）[1]，到如今的三维椭圆振动切削（3D-EVC）研究，椭圆振动辅助切削技术已被广泛应用于众多高精尖领域。 3D-EVC技术由于具有高效的加工特点得到重点关注，研究者针对3D-EVC 技术在装置设计与优化、切削力建模分析、颤振辨识与抑制等多个方面开展了深入研究[2-5]。

3D-EVC 主要是通过压电驱动器输出位移，经过结构的传递与合成来实现椭圆振动轨迹输出，而压电陶瓷材料固有的迟滞非线性将会影响其加工精度及系统内部的稳定性[6]。 然而针对3D-EVC 系统迟滞补偿的相关研究并不详尽，大多数研究对此采取忽略处理。

选用准确恰当的压电迟滞模型描述系统的迟滞非线性是迟滞补偿研究的重要基础。 压电迟滞建模的方法众多， 最常用的就是采用数学模型建模。该类数学模型类别众多，表达形式各有不同，其中就包含Preisach 模型[7]、Duhem 模型[8]和Bouc-Wen[9]模型等。 Bouc-Wen 模型是一种具有表达形式简洁直观特点的微分方程类数学模型，选择该模型可在节省大量复杂建模运算的同时，更好地服务于控制策略的设计。

参数辨识方法的优劣决定了模型辨识精度的高低。 近年来，诸如蝙蝠算法[10]、粒子群算法[11]、蚁群算法等[12]一系列元启发式人工智能算法在参数辨识领域得到了广泛关注。 然而，传统算法的提出与建立都遵循某些固定的机理，这就导致这一类算法都存在一定缺陷，如易早期收敛、寻优能力弱等。 因此，为了提高参数辨识精度和能力，针对传统算法的改进就显得尤为重要。

本文针对3D-EVC 系统进行迟滞建模和复合控制策略的设计，以补偿系统的迟滞非线性。 利用Bouc-Wen 模型描述3D-EVC 系统的迟滞非线性，并采用改进的花授粉算法对模型中的未知参数进行辨识，最终根据所建立的模型设计了“前馈-PID反馈”复合控制策略以补偿系统迟滞非线性，还通过设计实验证明该复合控制策略的有效性。

1 3D-EVC 系统压电迟滞模型的建立

非共振型3D-EVC 装置如图1 所示，该装置利用内部的压电叠堆驱动Y1、Y2和Z 三个轴向柔性铰链，促使刀尖形成三维椭圆运动轨迹。 压电叠堆由压电陶瓷材料构成，其固有的迟滞非线性会导致系统无法按照给定的理想输入来输出三维椭圆运动轨迹。 本文利用Bouc-Wen 迟滞模型描述3D-EVC系统输入电压与输出位移之间的关系，通过该模型来准确刻画3D-EVC 系统存在的复杂迟滞现象，为后续复合控制策略的设计奠定高精度的理论模型基础。

图1 3D-EVC 装置结构

1.1 Bouc-Wen 模型

Bouc-Wen 滞回模型最早是被用来表示早期的模拟金属阻尼器精度较高的实用滞回模型。 现在，Bouc-Wen 模型已被广泛应用于描述土木、 机械等领域中的非线性现象，其数学表达式为：

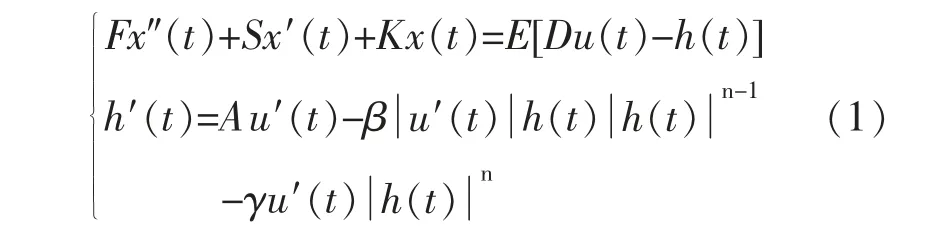
在正常加工状态下，3D-EVC 系统的三相驱动均属于低频率输入，因此式（1）中的Fx″（t）可忽略不计。 为了保证系统的可靠性，每次进行测量数据采集时，均需对位移传感器进行重新标定，因此式（1）中的初始位移也可忽略不计。

综合考虑以上因素后的Bouc-Wen 模型表达式可表达为：

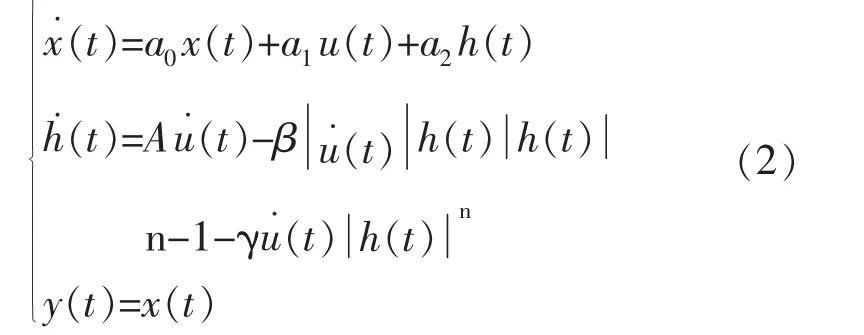
式中：a0、a1、a2、A、β、γ、n 均为待辨识参数。

1.2 改进花授粉算法

花授粉算法作为一种新型的群智能优化算法，近年来被用以解决相关的实际问题。 该算法受启发于自然界的花授粉过程[13]，执行寻优操作依靠全局授粉（全局搜索）和局部授粉（局部搜索）两个阶段。

全局授粉阶段的表达式为：

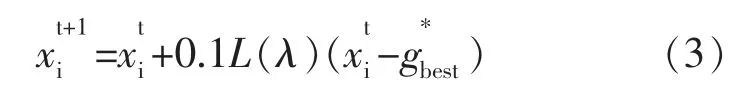
局部授粉阶段的表达式为：

为了提高算法的收敛速度和寻优能力，在花授粉算法前期引入粒子群算法使其更靠近最优解范围，从而提高寻优速度；在算法后期，引入自调节转换概率p 来调节全局搜索和局搜索在整个搜索过程中的比例，从而提高收敛速度。

自调节转换概率p 可表示为：

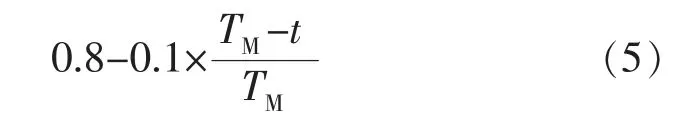
式中：TM为最大迭代次数； t 为当前迭代次数。

通过引入前期粒子群算法（PSO）和自调节转换概率p 后，经改进的花授粉算法（IFPA）将在一定程度上克服传统算法的弊端，从而提高自身算法的寻优能力、加快寻优收敛速度，并为获得更高精度的Bouc-Wen 迟滞模型提供有效的算法辨识手段。

1.3 模型参数辨识

为了对Bouc-Wen 模型中含有的未知参数进行辨识， 从而准确描述3D-EVC 系统压电迟滞特性，本文通过如图2 所示实验平台得到一定频率下的输入电压-输出位移曲线； 对3D-EVC 系统给予一个正弦激励信号： y（t）=5+5sin（100πt+π/2），得到在该正弦激励信号下的激励相应曲线；利用改进后的花授粉算法对Bouc-Wen 模型进行参数辨识； 通过辨识得到3D-EVC 系统Bouc-Wen 模型（表1）。

表1 3D-EVC 系统参数辨识结果

图2 实验平台

本文选用均方根误差（MSE）作为模型辨识的目标适应度函数，用来评价模型辨识精度。均方根误差（MSE）表达式为：

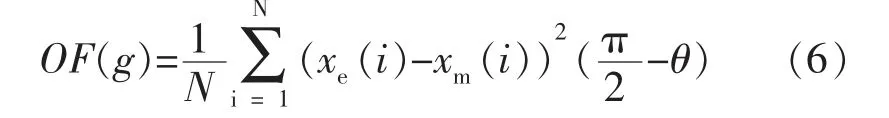
式中：xe为实际输出位移数据；xm为模型输出位移数据；N 为数据总个数。

3D-EVC 系统具有Y1、Y2和Z 三个轴向， 每一个轴向子系统都可被视作为一个单输入、输出子系统。 由于三个轴向子系统的压电迟滞模型参数辨识方法一致，本文以Y1轴向子系统为例进行研究。 验证改进后的花授粉算法针对Bouc-Wen 模型参数辨识的效果见图3。

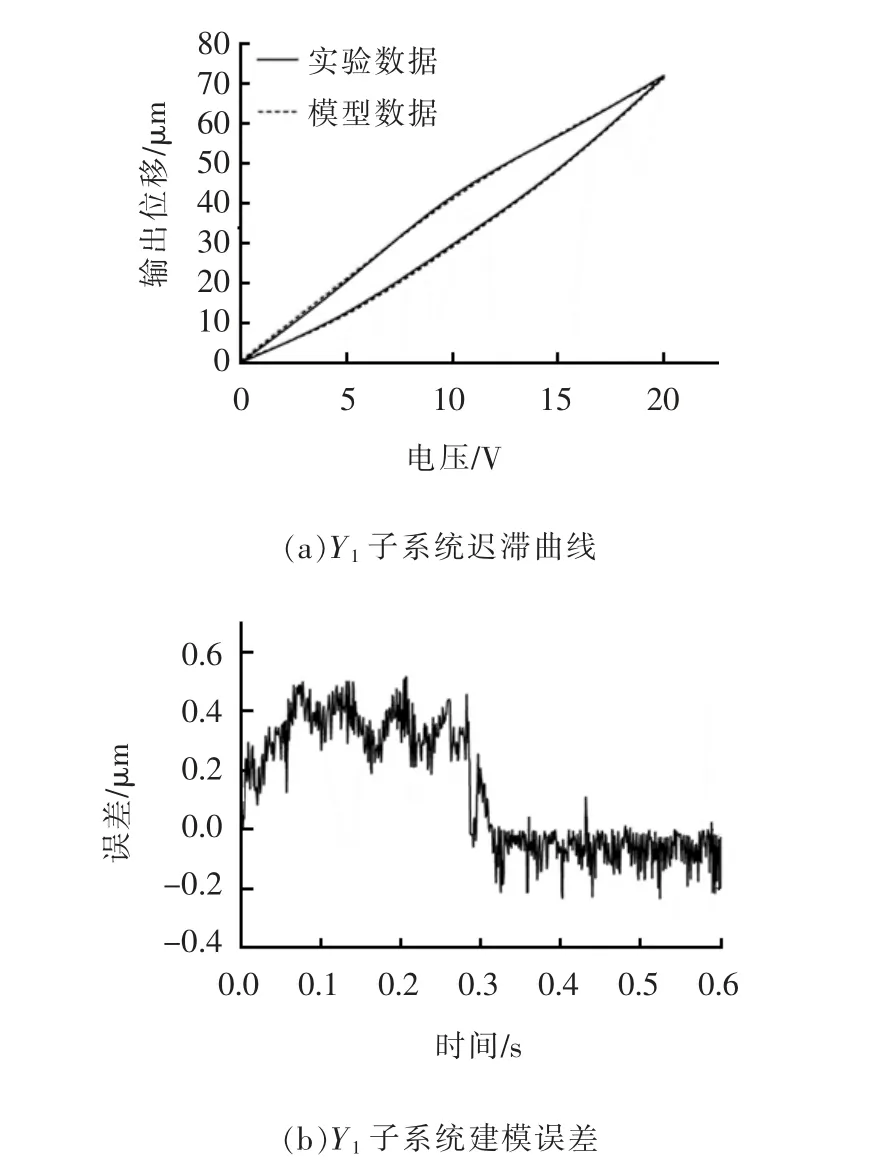
图3 Y1 轴向子系统迟滞拟合

由图3 可得，Y1轴向子系统的最大建模误差为0.5074 μm、建模精度为98.24%。 由Y1轴向子系统迟滞曲线拟合及系统建模误差可见，利用改进后的花授粉算法辨识得到的Bouc-Wen 模型可有效地描述3D-EVC 系统所表现出的压电迟滞非线性，具有较高的建模精度。

2 基于压电迟滞模型的3D-EVC 系统复合控制策略

2.1 前馈补偿控制策略

前馈补偿控制策略是3D-EVC 系统复合控制策略的基础。 由式（2）可知，本文选用的Bouc-Wen模型表达式有线性部分和迟滞非线性两部分，因此不同于其他迟滞模型需求解复杂的迟滞逆模型数学表达式来进行前馈补偿，Bouc-Wen 模型仅需对迟滞分量部分的电压进行补偿，即可补偿系统所表现的迟滞非线性。

假定输入电压为uI（t），经前馈补偿后的输出电压为uF（t），代入式（2）并整理得到：

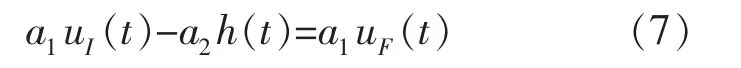
由式（2）中的迟滞分量部分表达式可知，为了求得输出量uF（t），首先利用uI（t）近似替代uF（t），求解得出迟滞分量估计值h^（t）。 此时，基于前馈补偿的Bouc-Wen 模型表达式为：

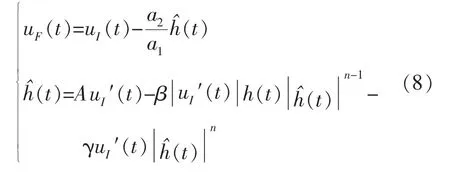
由于近似计算导致迟滞分量部分产生误差，因此系统实际输出位移xA（t）为：

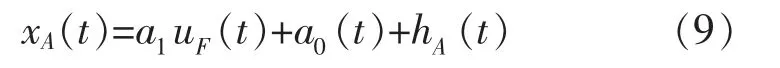
式中：hA（t）为实际迟滞分量。

综上所述，利用前馈补偿控制得到的系统误差表达式为：

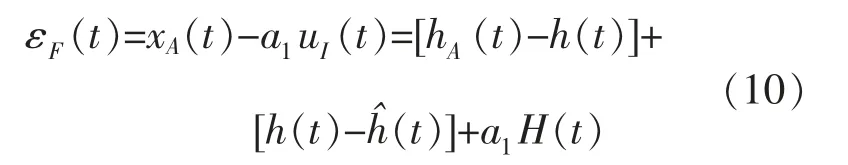
2.2 复合控制补偿策略

前馈控制本质上属于一种开环控制，无法满足系统对于持续稳态的要求。 为了消除误差，提高控制系统精度，本节将引入反馈控制搭建“前馈-PID反馈”复合控制策略。

在工业控制系统中，PID 控制已被广泛应用于多种系统回路的协同控制， 取得了一定的良好效果。PID 控制算法是一种基于偏差信号的控制算法，偏差的产生是由于被控对象实时监测输出，然后以反馈形式回馈到控制输入端。PID 控制器的输入、输出关系为：

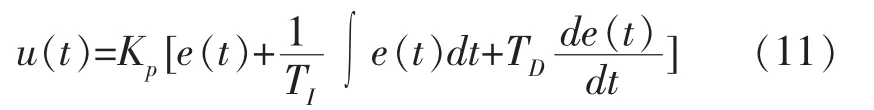
即：

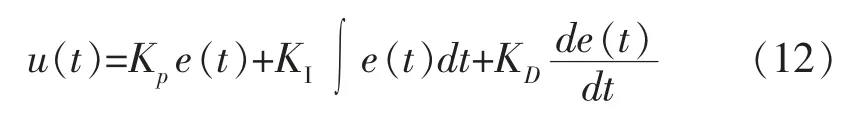
其中，

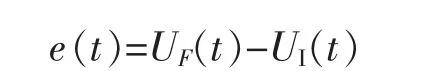
3D-EVC 系统复合控制策略框图见图4。

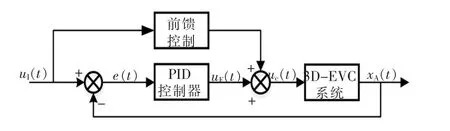
图4 复合控制策略

3 实验验证

本文基于上节设计的“前馈-PID 反馈”复合控制策略对3D-EVC 系统进行迟滞补偿， 并采用图2所示实验平台进行验证。 实验验证时，以Y1轴向子系统为例，通过设定预期轨迹，采用上位机控制NI控制器， 并通过功率放大器作用至3D-EVC 装置，最终通过位移传感器返回数据至上位机形成闭环，采集实际输出轨迹以验证所设计的复合控制策略的有效性。 图5 是经复合控制策略后系统迟滞跟踪曲线图，图6 是Y1轴向子系统实验跟踪轨迹曲线及误差图。

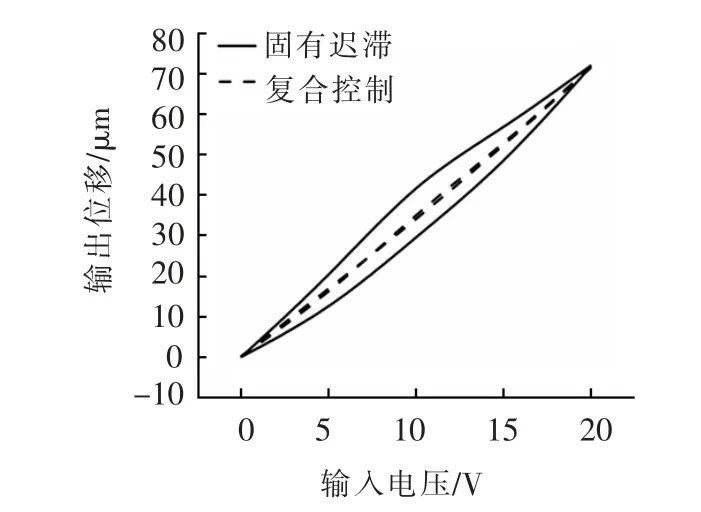
图5 迟滞跟踪曲线图

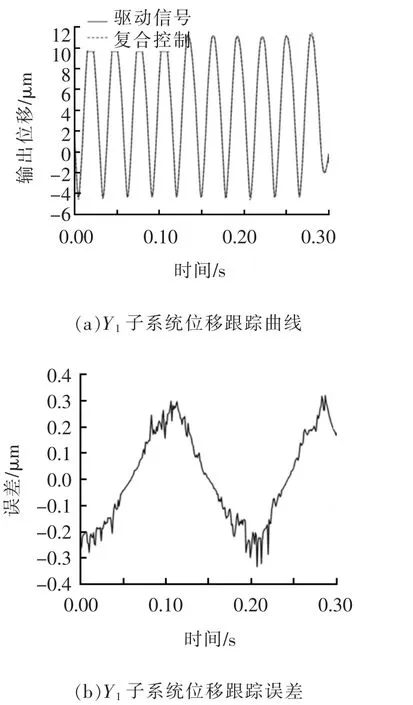
图6 Y1 轴向子系统跟踪轨迹曲线及误差

从图5 和图6 对Y1子系统的分析可看出，利用本文设计的复合控制策略对3D-EVC 系统进行迟滞补偿校正后，系统迟滞分量明显减小，最大位移跟踪误差为0.304 μm。 实验结果证明，经复合控制策略补偿校正后的3D-EVC 系统，其迟滞现象得到明显改善，系统的跟踪性能也得到明显的提升。

4 结论

压电陶瓷材料固有的迟滞非线性是影响3DEVC 系统性能和装置三维椭圆轨迹输出的重要因素。 本文利用Bouc-Wen 模型描述系统压电迟滞特性， 并利用改进后的花授粉算法对Bouc-Wen 模型中的未知参数进行辨识，以提高模型的参数辨识精度，还基于辨识得出的Bouc-Wen 模型设计“前馈-PID 反馈”复合控制策略，对3D-EVC 系统进行迟滞补偿研究，得到以下结论：

（1）利用复合控制策略补偿3D-EVC 系统迟滞非线性后，系统的迟滞分量明显较小，有效地减弱了迟滞性。

（2）以正弦信号激励系统，系统位移跟踪实验结果证明，3D-EVC 系统在复合控制策略下具有较高的位移跟踪性能， 其位移跟踪误差最大为0.304 μm，证明系统具有更好的鲁棒性和跟踪性能。