一种具有高抑制特性的小型化SIW 滤波器的设计

黄玉兰,兰 静,黄令超

(西安邮电大学电子工程学院,陕西 西安 710121)

随着无线通信行业的迅速发展,滤波器作为一种选频器件,有着广泛的应用前景。在常见的无线收发系统中,每一步都需要加载滤波器来滤除噪声,从而保证射频系统的稳定性,因此滤波器对无线收发系统的传输质量有着至关重要的影响。为满足现代无线通信要求,研究者们在高带外抑制、低插损、小型化等方面做了大量的研究[1]。近年来,基片集成波导(SIW)凭借其高品质因数、易集成、大功率容量等独特优势逐渐被广泛应用,常见的SIW 滤波器的设计方法有1/n模切割法[2]、多层折叠法[3]、多模交叉耦合[4]以及表面加载法[5]等。

文献[6]利用不同模态的SIW 腔提供宽阻带响应和高选择性,但其插损及回波损耗不理想。文献[7]通过加载谐振器使得滤波器共有三个传输零点,一定程度上提高了带外抑制,但由于其传输零点多,设计复杂,导致不够小型化。文献[8]通过增加金属孔,使得滤波器有更高的品质因数,但其插损较大,无法满足现代通信系统低插损的要求。文献[9]通过垂直叠加三个SIW 腔,使滤波器变得更加紧凑,通过调整相邻SIW 腔间的耦合系数来独立控制传输零点,但仍存在插损较大的问题。文献[10]通过改变浮动圆盘的大小,调整谐振模式,改变馈线间的夹角对传输零点进行控制,该滤波器灵活性很大,但其带外抑制性能较差。文献[11]在SIW 表面刻蚀两个反向排列的方形互补裂环谐振器,实现了滤波器的小型化,但其带外抑制性能并不理想。

结合以上文献可知,很多滤波器设计难以兼顾高带外抑制、低插损及小型化等特点。为解决以上问题,本文基于电偶极子加载的隐失模理论[12],首先设计了单级滤波器;其次,在单级滤波器上进行改进,使用电磁仿真软件HFSS 进行优化调节,得到带外抑制更高及带宽更优的双级滤波器;最后通过实物测量结果验证了该设计的有效性。本文降低了滤波器结构的复杂度,得到了一款低插损、高带外抑制、小型化可应用于5G(Sub-6 GHz)通信系统中的滤波器。

1 单级SIW 滤波器设计

1.1 单级SIW 滤波器结构

图1 为单级滤波器结构图,采用Rogers RT/Duroid 5870 介质基板,其厚度为0.787 mm,相对介电常数为2.33。该结构包括矩形SIW 腔以及一对面对面的矩形谐振环,SIW 腔中包括两排金属通孔,用以等效波导的侧壁。

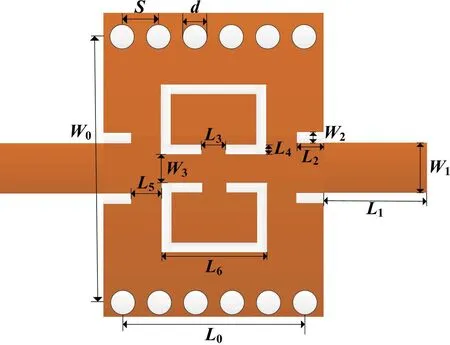
图1 单级滤波器结构图Fig.1 Single-stage filter structure diagram

设计SIW 腔的基本结构,需考虑以下参数,如SIW腔的宽度W和等效宽度Weff以及通孔直径d、通孔间距S等。其中等效宽度计算公式为:

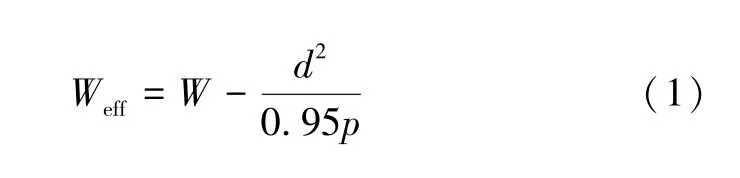
当通孔间距满足公式(2)时,近似地认为此时腔内无电磁能泄露。

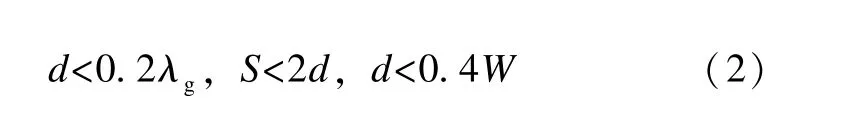
根据文献[16]可得截止频率计算公式为:

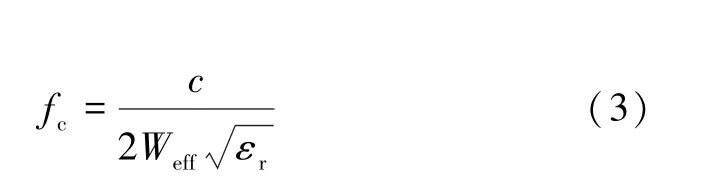
式中:c为光速;εr为介电常数。由式(3)计算可得SIW 腔的截止频率为10.3 GHz。

1.2 工作原理

SIW 具有高通性能,可作为高通滤波器使用。为设计带通滤波器,需要一种具有带阻性能的电磁结构来实现理想的性能。如图2 所示,在主模传播情况下,SIW 内部的电场垂直分布于其顶部金属层和底层,磁场方向平行于波导表面,垂直于波导侧壁。根据电偶极子加载的隐失模理论,由于互补开口谐振环(CSRR)或表面刻蚀缝隙[13-14]等结构的负磁导率特性可在谐振频率附近产生较强的带外抑制,加载矩形谐振环会使得谐振腔内部电场发生变化,增加表面电流路径,从而产生一个低于SIW 腔截止频率的通带(此通带是由图2 所示的轴向电场激发引起的)。本文将矩形谐振环结构蚀刻在SIW 的上金属面,使得滤波器实现小型化[15-16],改变传统的馈电方式,矩形谐振环间耦合增强,传输零点衰减增大。

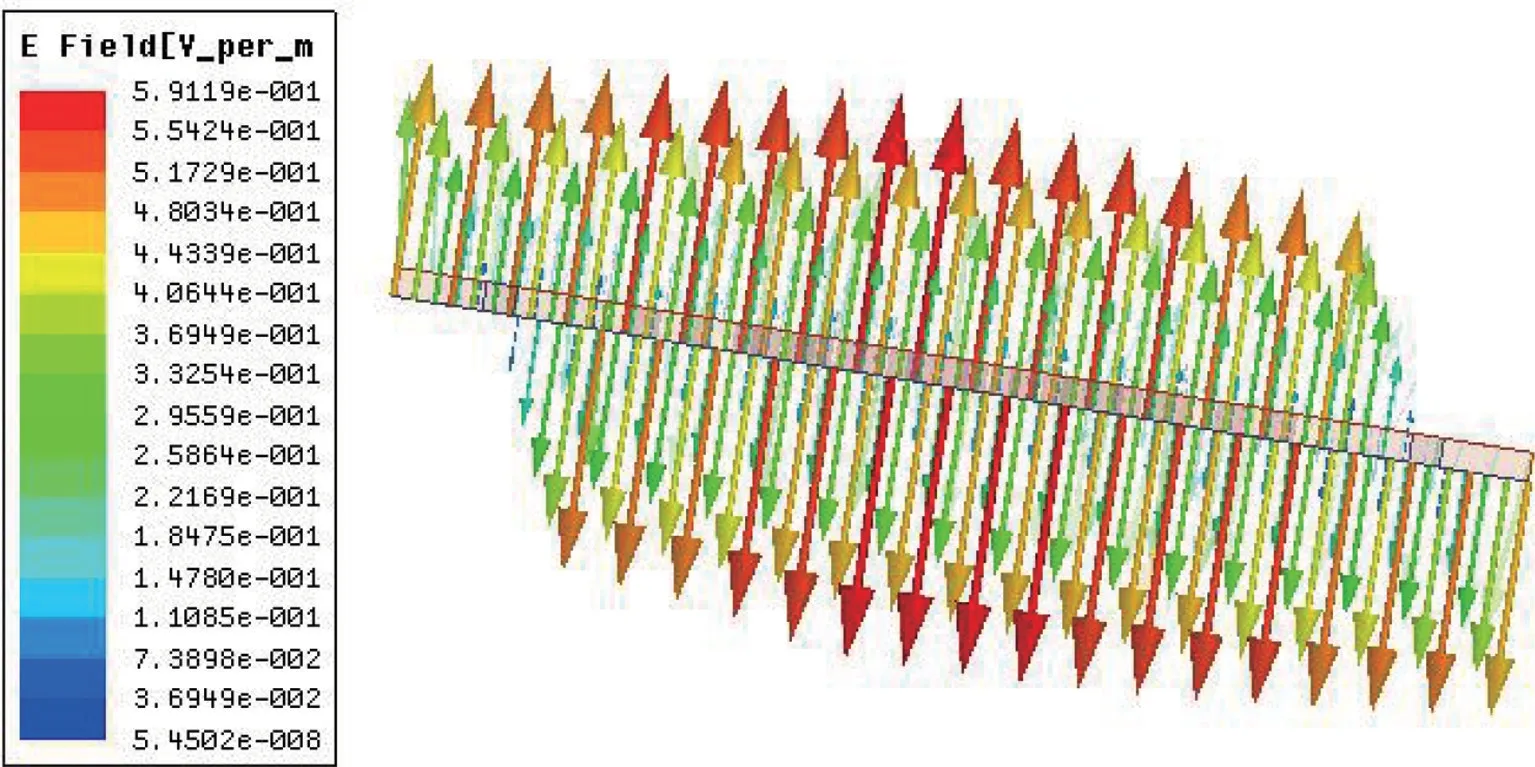
图2 电场分布图Fig.2 Electric field distribution diagram

图3 为单级SIW 滤波器的等效电路模型。将SIW中的上下两排金属通孔等效为并联电感,用Lvia表示;两个矩形谐振环作为分流谐振器,由电容Cr和电感Lr组成,谐振腔提供了带通特性和SIW 的高通特性;其中波导传输线与矩形谐振器之间存在耦合,用Lc及Cc表示电感和电容耦合。使用ADS 对等效电路模型进行仿真,根据图4 可知,等效电路模型为实际滤波器的一个简化电路。在所设计的频段范围内,与单级滤波器仿真结果基本一致,验证了其等效关系。

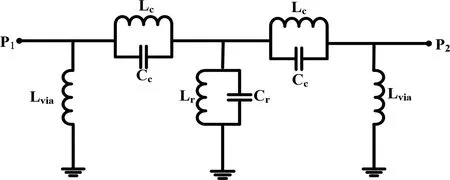
图3 单级滤波器等效电路模型Fig.3 Single-stage filter equivalent circuit model

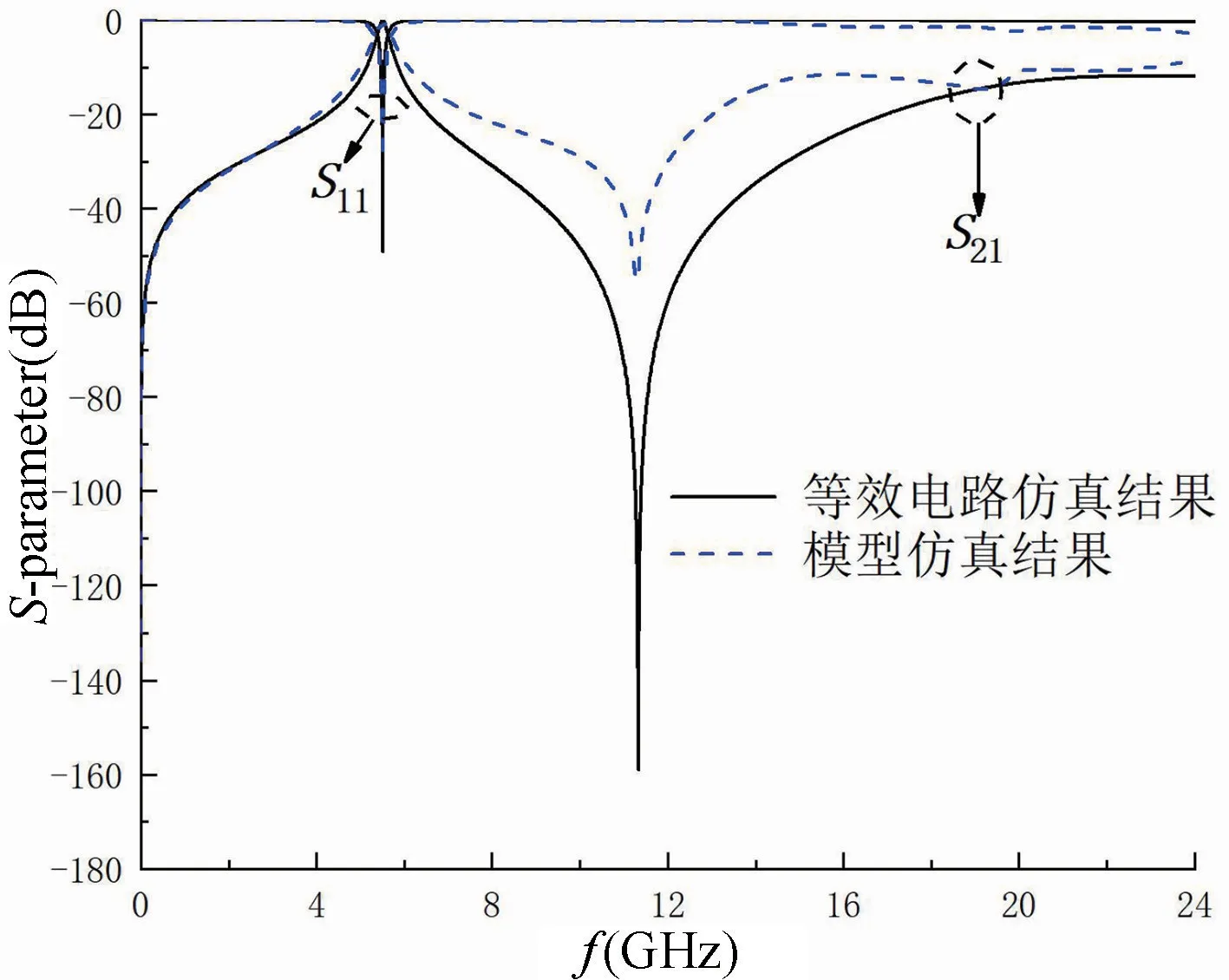
图4 单级滤波器与等效电路仿真结果对比图Fig.4 Comparison of single-stage filter and equivalent circuit simulation results

单级滤波器的传输零点是由SIW 谐振腔和矩形谐振环之间输入输出电磁混合耦合产生的,式(4)为传输零点计算公式:

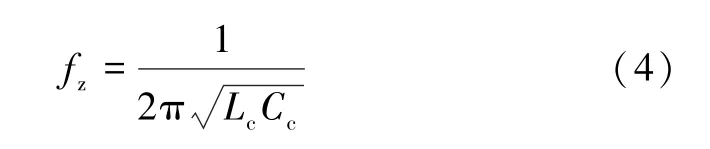
由式(4)可求得传输零点位于11.29 GHz 处,与仿真结果基本吻合。

1.3 结果与分析

使用HFSS15.0 进行仿真优化,单级滤波器S参数随不同参数变化仿真曲线如图5 所示。图5(a)为S参数随W3变化的仿真曲线,随着W3的增大,滤波器的中心频率往高频移动。其原因是随着耦合间距W3增大,等效电路中电感减小,使频率增加,传输零点向高频移动。图5(b)为S参数随L4变化的仿真曲线,同图5(a)变化规律相同,其原因是随着L4增大,等效电路中电感减小,频率及传输零点向高频移动,其中L4对传输零点影响较大。如图5(c)所示,当L6增大时,滤波器谐振频率减小,往低频方向移动。其原因是L6增大使得整个谐振腔电长度增加,导致滤波器谐振频率降低,传输零点向低频移动。实验表明,可通过调节以上参数达到优化单级滤波器S参数的目的。

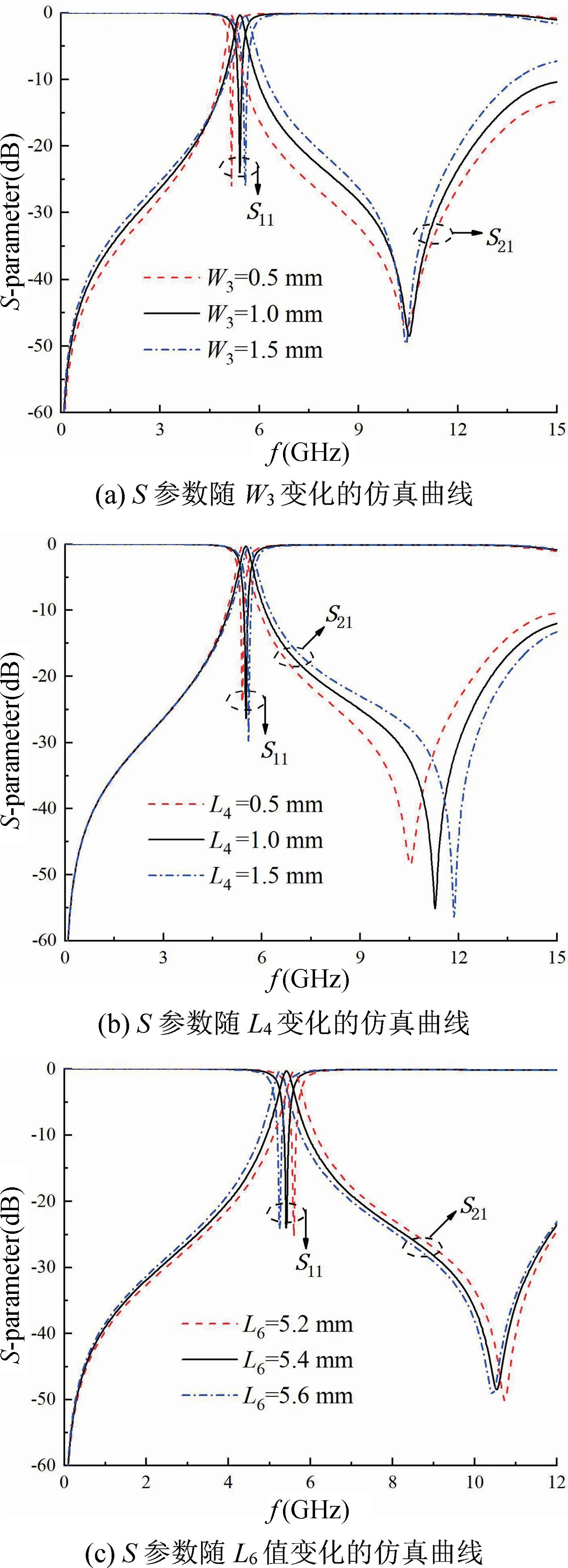
图5 S 参数随不同参数变化仿真曲线图Fig.5 Simulation graphs of S-parameter variation with different parameters

单级滤波器经上述参数优化后最终仿真结果如图6 所示,所设计的滤波器中心频率为5.5 GHz,相比于SIW 腔的截止频率10.3 GHz,中心频率下降了46.6%,其原因是通过加载矩形谐振环,谐振腔内部电场发生改变,从而影响金属上表面的电流分布,使得中心频率降低,实现了小型化。其相对带宽6.9%,最小插入损耗仅为0.29 dB,回波损耗优于29.49 dB,在7.59～12.99 GHz 频带范围内带外抑制大于20 dB,在11.29 GHz 处存在一个传输零点,最大衰减为55.11 dB,提高了滤波器的选择性及带外抑制。

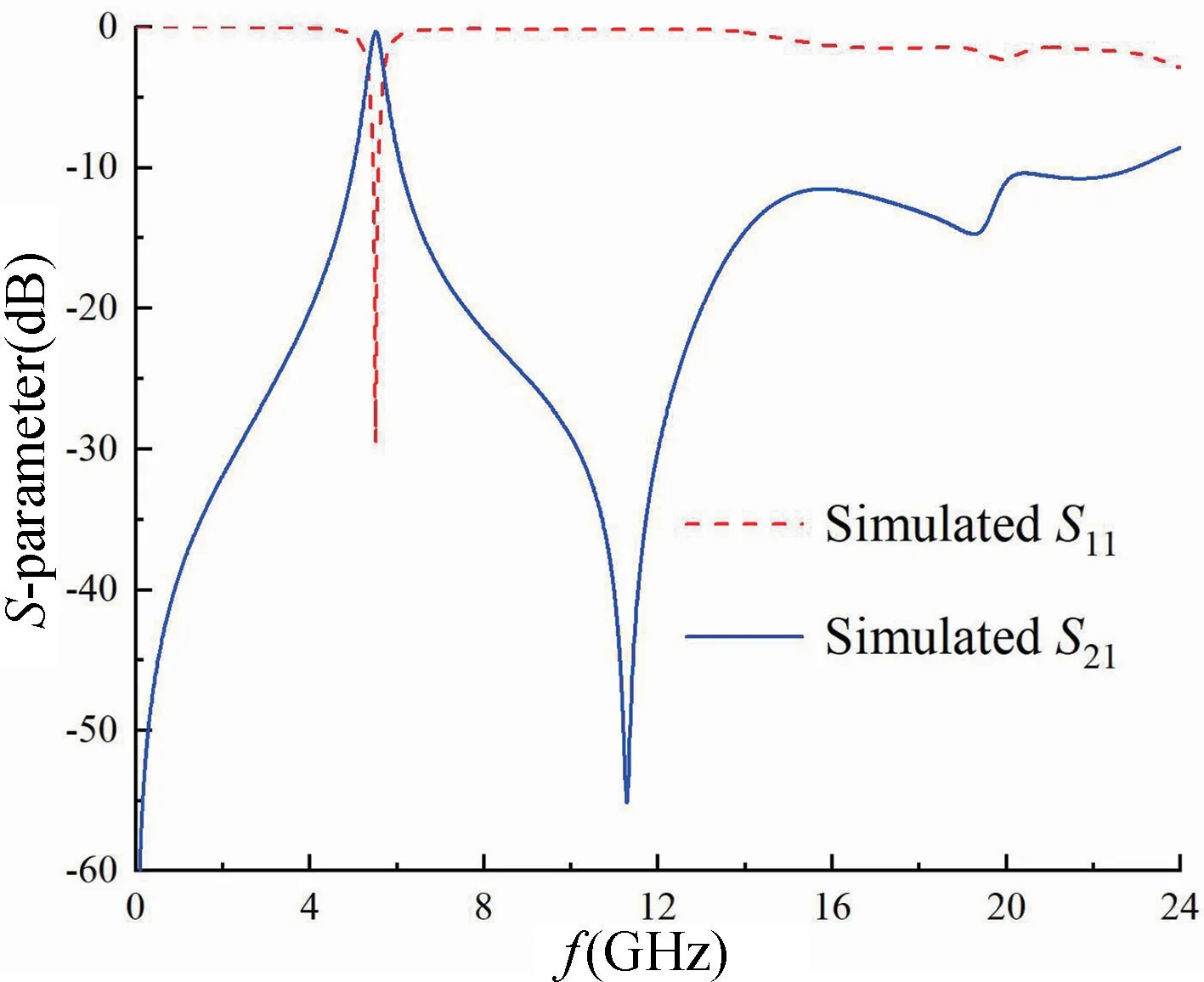
图6 单级滤波器仿真结果图Fig.6 Simulation results of a single-stage filter

2 双级滤波器的设计

2.1 双级SIW 滤波器结构

为设计具有阻带宽、插损小等特性的滤波器,在单级的基础上进行改进,提出双级滤波器,其结构如图7 所示。根据实际情况,将基板长度L0设置为15 mm,在SIW 的顶层刻蚀两对矩形谐振环,选取合适参数达到设计要求。该双级滤波器矩形谐振环的长边长度为L7,两对矩形谐振环间的距离为L3,调整两边馈线的长度及宽度,实现阻抗匹配。表1 为优化后双级滤波器的尺寸参数。

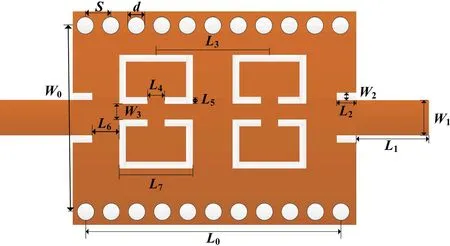
图7 双级滤波器结构图Fig.7 Two-stage filter structure diagram

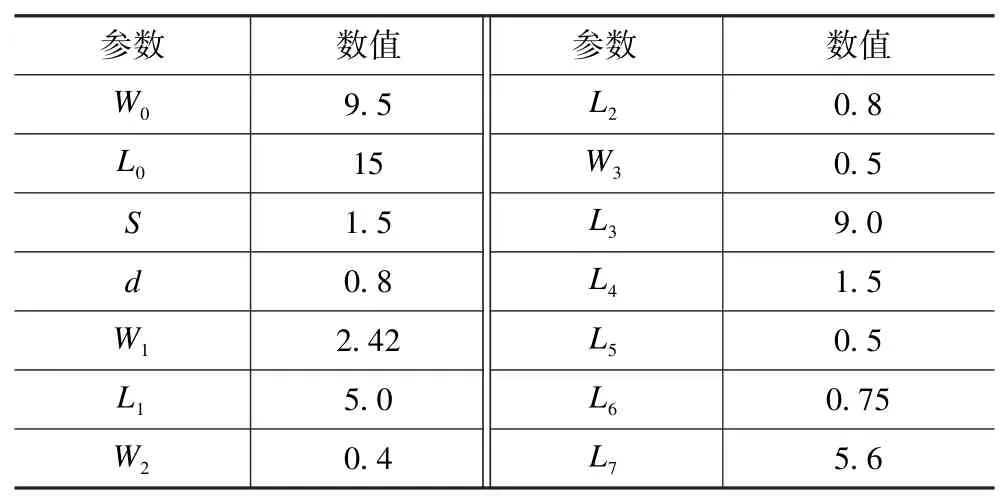
表1 双级滤波器参数Tab.1 Two-stage filter parameters mm

2.2 工作原理

由于双级滤波器是在单级滤波器基础上所改进的,因此双级滤波器电路等效模型也将进行相应变化。双级滤波器等效电路模型如图8 所示,由于新增加的两对矩形谐振环之间存在耦合,因此在原等效模型基础上,新增两对耦合谐振器,分别为Lr和Cr以及L0和C0。其中Lr和Cr与单级滤波器的耦合槽相似,L0和C0表示两对矩形谐振环间的耦合,将L0和C0加载在两个谐振腔之间,使得等效模型成立。将等效电路模型在ADS 中仿真,双级滤波器与等效电路仿真结果对比如图9 所示,等效电路模型在所设计频带范围内与双级滤波器的仿真结果基本一致,验证了其等效关系。

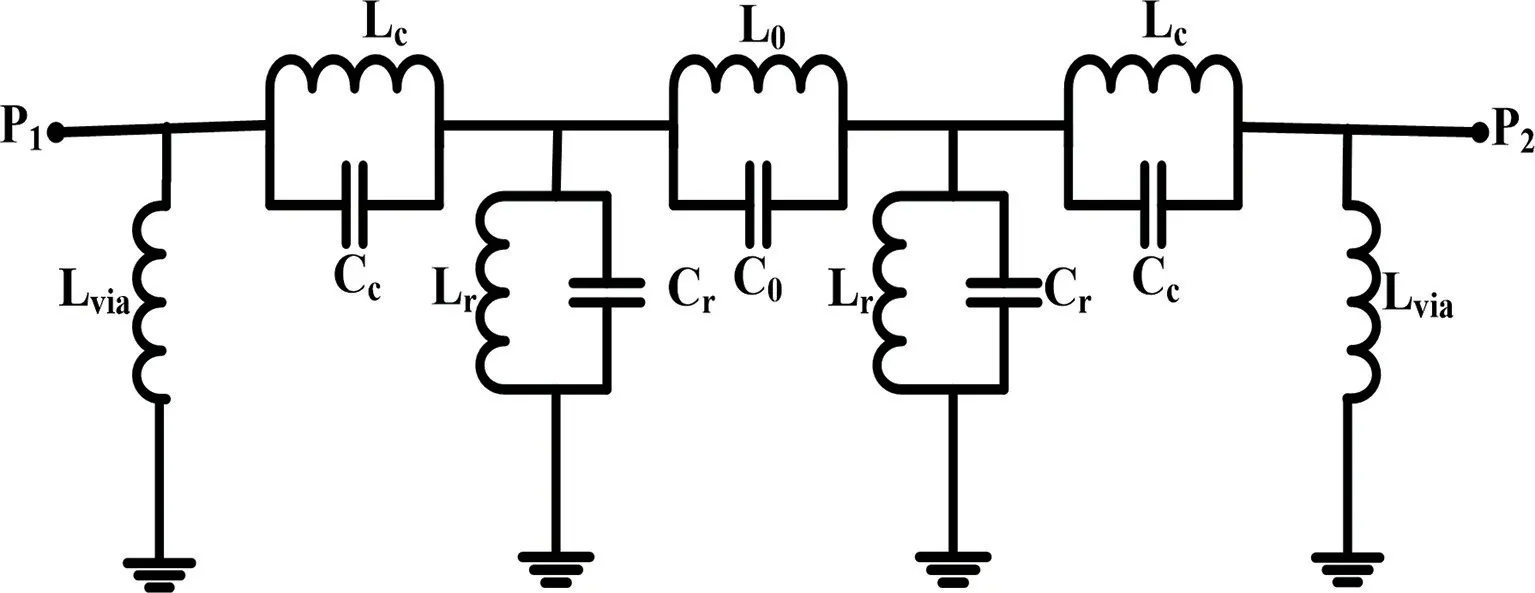
图8 双级滤波器等效电路模型Fig.8 Two-stage filter equivalent circuit model

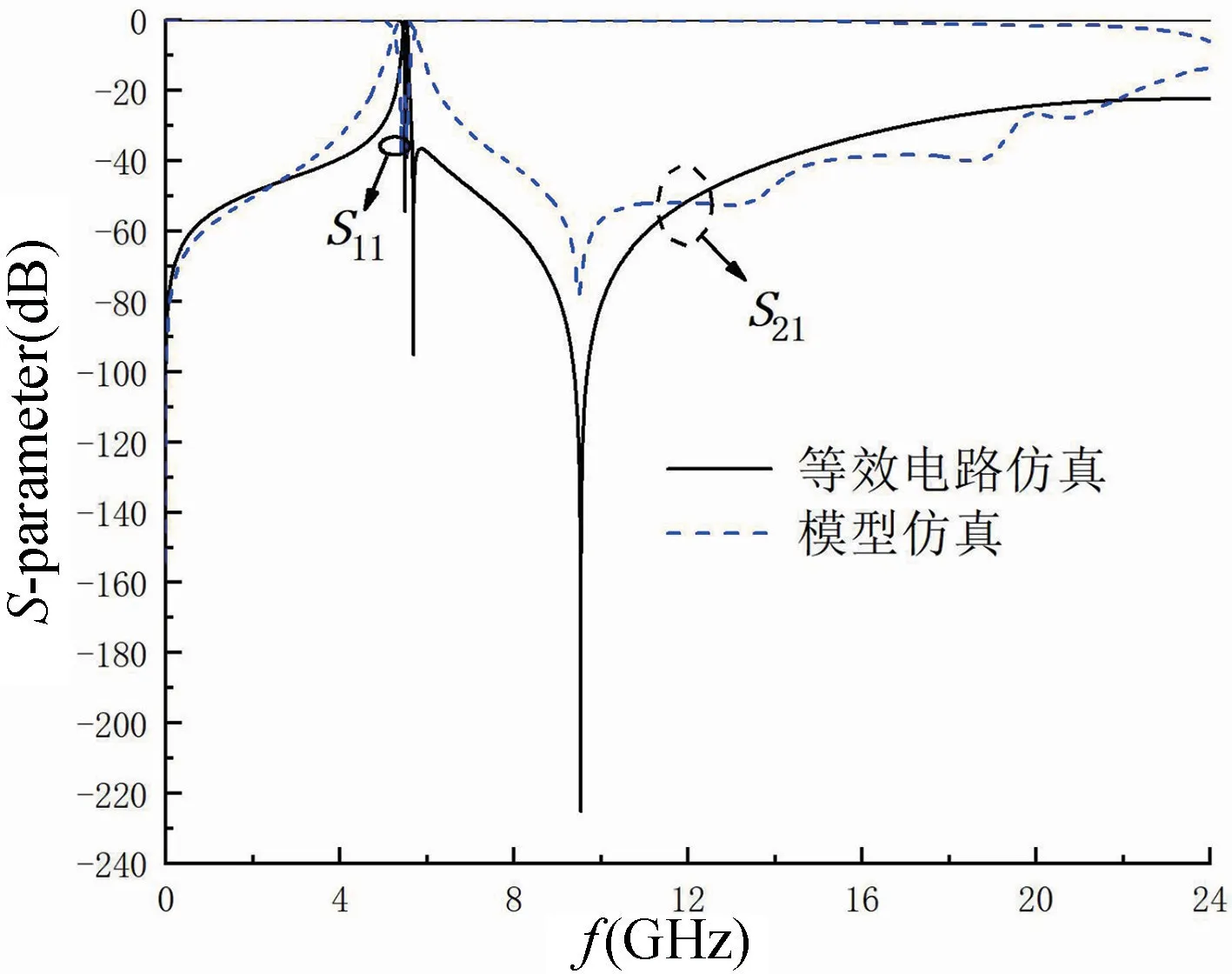
图9 双级滤波器与等效电路仿真结果对比图Fig.9 Comparison of two-stage filter and equivalent circuit simulation results

2.3 传输响应分析

图10 为S参数随着L3值变化的仿真曲线,随着L3增大,滤波器的带宽变窄,其原因是随着L3增大,两对矩形谐振环间的耦合逐渐减弱,两个谐振频点相互靠近,从而导致带宽变窄;反之亦然。由此可得,该滤波器带宽由两对矩形谐振环之间耦合强度决定。

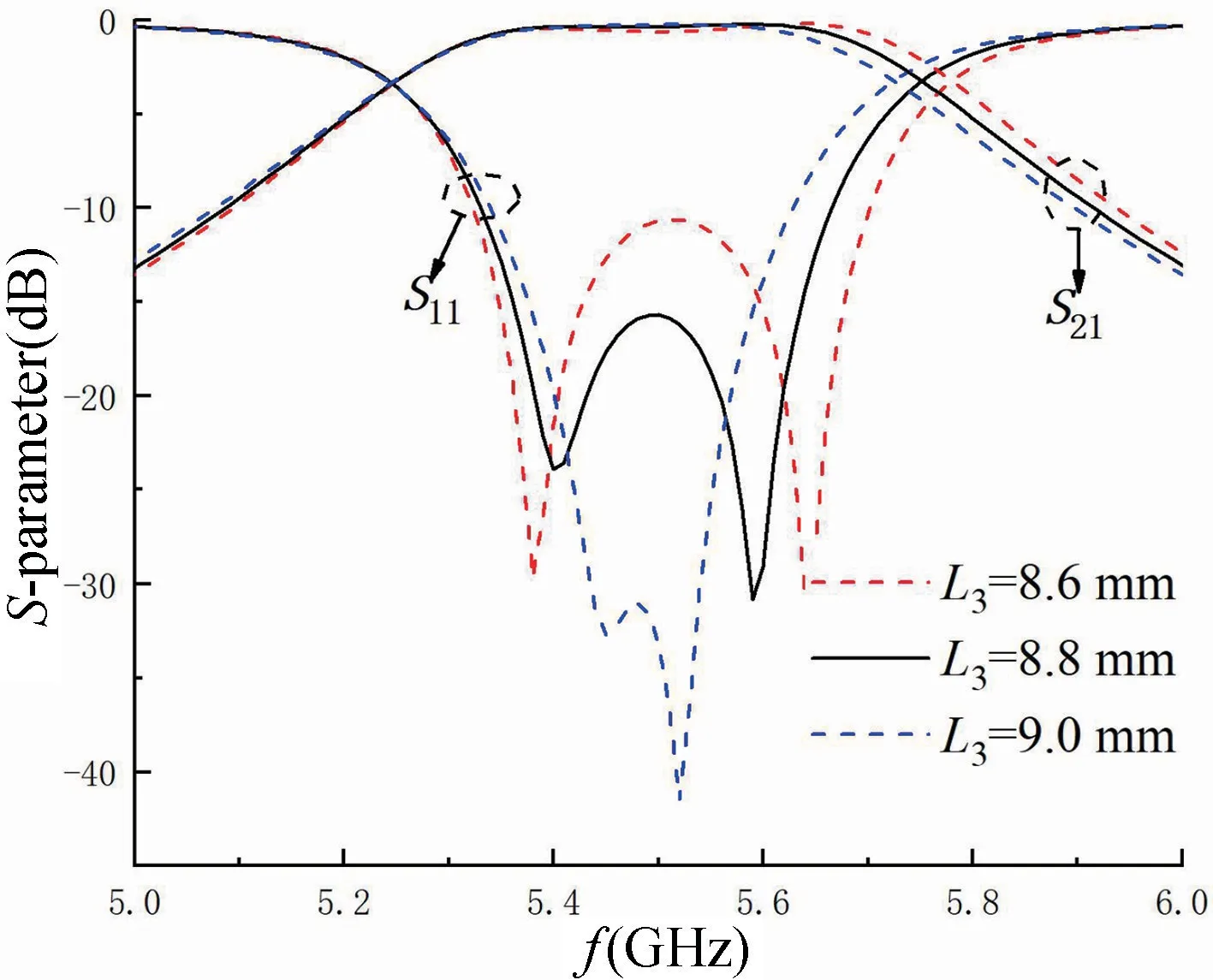
图10 S 参数随L3值变化的仿真曲线Fig.10 Simulation curves of S-parameter variation with L3 value

2.4 仿真和测试结果

为验证设计结果的有效性,采用Rogers 5870 介质基板,其厚度为0.787 mm,相对介电常数为2.33,对所设计滤波器进行实物加工。滤波器实物图如图11 所示,滤波器的有效尺寸为15 mm×9.5 mm(不包括输入输出端口),电长度为0.818λg×0.348λg,其中λg为中心频率处的导波波长。

图11 滤波器实物图Fig.11 Photograph of the fabricated filter

利用矢量网络分析仪进行实物测试,图12 为滤波器S参数仿真与实物测试对比结果,其中右下角插图为5～6 GHz 频段内仿真及测试回波损耗S11的局部放大图。仿真结果显示其中心频率为5.5 GHz,带内最小插入损耗为0.27 dB,回波损耗大于21.9 dB,相对带宽为8.5%,带外抑制在6.22～22.3 GHz 频带范围内大于20 dB,存在一个传输零点位于9.48 GHz 处,最大衰减为77.48 dB;测试结果显示,该滤波器中心频率为5.5 GHz,插入损耗仅为0.64 dB,回波损耗大于16.9 dB,带外抑制也实现了预期目标。实物测试数据与仿真结果有一定误差,造成上述误差的原因有接头损耗及焊接误差等。测试结果与仿真结果吻合度较高,较好地验证了设计的有效性。

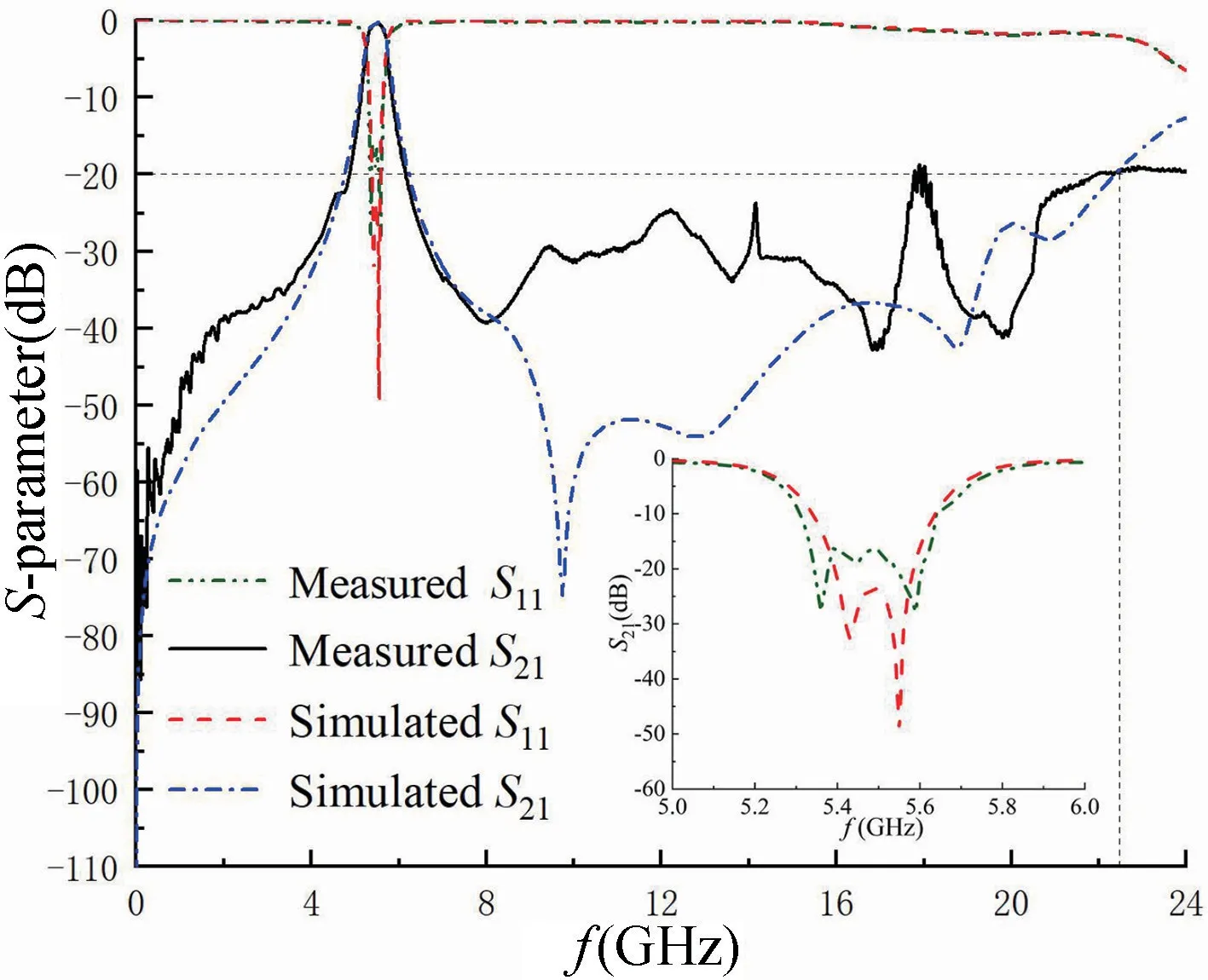
图12 滤波器S 参数仿真与实物测试结果Fig.12 S-parameter measured and simulated results of the filter

表2 为本文所设计的双级滤波器与其他文献滤波器的性能参数对比。可得,该滤波器插入损耗和回波损耗均优于其他文献,阻带宽度更宽,带外衰减更大,极大地提高了滤波器的频率选择性。总体来说,该滤波器在插损、带外抑制及尺寸等方面均有显著的提升。

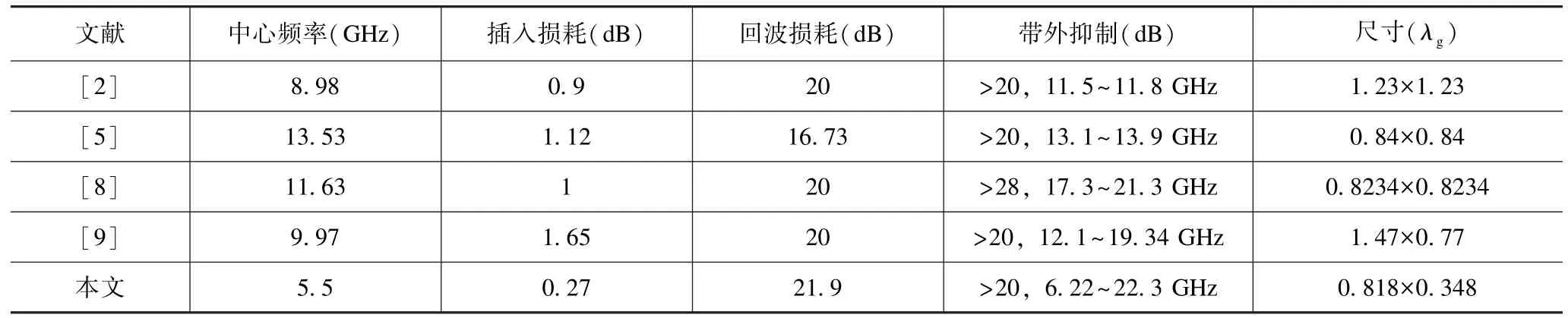
表2 双级滤波器性能参数对比Tab.2 Comparison of performance parameters of two-stage filter

3 结论

本文基于隐失模理论设计了一款具有高抑制特性的小型化SIW 滤波器,该滤波器有效尺寸仅为15 mm×9.5 mm(0.818λg×0.348λg)。该滤波器中心频率为5.5 GHz,通带范围5.25～ 5.72 GHz,插入损耗仅为0.27 dB,回波损耗大于21.9 dB。在6.22～22.3 GHz频段内带外抑制大于20 dB,传输零点位于9.48 GHz处,最大衰减为77.48 dB。加工实物并测试验证了设计的有效性。该滤波器具有低插损、高带外抑制、小型化的特点,在5G(Sub-6 GHz)通信系统中有一定的应用价值。