锂电池极片缺陷特征融合与分类

黄梦涛 王 露

（西安科技大学电气与控制工程学院，西安 710000）

0 引言

经济的发展带动能源需求增加，锂电池由于零排放、体积小、使用寿命长等优点广泛应用于电动汽车、电子产品等领域。极片作为锂电池的要件直接决定其电化学性能及安全性[1]，但是极片在涂覆、辊压等生产环节可能会产生各种缺陷，通过缺陷检测可防止不良品流向市场，避免安全事故发生。对缺陷分类便于企业分析缺陷产生的原因并做出相应的调整，从根源上降低甚至避免极片缺陷的产生，减少经济损失。

随着计算机和机器视觉技术的发展，基于图像处理的极片缺陷分类方法得到广泛应用。将提取的特征输入分类器中训练分类模型，然后利用模型预测分类。特征提取作为其中的关键步骤，对分类性能有直接性影响[2]。本文将主要研究特征提取，现有方法中主要提取极片缺陷的形状特征和灰度特征[3-6]，但是缺陷的形状大小和数目具有不确定性，而且形态特征参数的准确性易受图像分割效果的影响。除此之外，还要考虑光线等环境因素对极片图像的影响。本文对极片的划痕缺陷、掉料缺陷和暗斑缺陷分类时，提出局部SURF特征与灰度特征融合的方法。前者可以避免光照的影响，后者从全局角度分析极片缺陷，两种特征融合对缺陷的描述更全面。目前，特征融合在人脸识别[7]、车辆检测[8]及医学图像[9]等多方面有所应用。

1 极片缺陷BoF-SURF特征提取

1.1 SURF特征提取

SURF（Speeded Up Robust Feature）是Herbert Bay等提出的一种局部特征，不仅对尺度、旋转和噪声等因素具有很强的不变性，而且对光照和仿射透射变化具有一定的鲁棒性[10]。在SURF算法中，将图像中的点与二阶高斯模板卷积，构建Hessian矩阵如式(1)并利用其行列式是否大于零来寻找局部极值点。

为加速运算，使用盒子滤波近似代替二阶高斯模板。然后逐渐增大盒子滤波器的模板尺寸构建尺度空间。Hessian矩阵近似判别式表达如下：

其中Dxx，Dxy，Dyy是盒子滤波与图像的卷积。

将经过Hessian矩阵处理的像素点与其领域内的26个点比较大小，若该点是其中最大或最小值则作为候选特征点保留，再进行插值运算确定最终特征点。

以特征点为中心，以6δ（δ为特征点尺度）为半径统计60°扇形邻域内harr小波响应值总和，并以一定间隔旋转该邻域遍历整个圆形区域，响应值最大的扇形对应的方向即为该特征点的主方向。沿主方向取边长为20δ的方框，并划分为16个子区域，统计每个子区域的haar小波响应值，得到4维特征向量表示，因此每个特征点就是64维向量。

1.2 SURF特征的BoF量化

通过以上步骤得到极片缺陷图像的SURF特征向量集合，每个特征向量是64维，但是每张图像提取到的SURF特征点数目不一样，不能直接作为分类器的输入。所以采用Bag-of-feature（BoF）模型对SURF特征进行量化。

BoF方法源于文本处理的词袋模型（BoW），将图像看成是若干个特征的无序集合。首先提取极片缺陷的SURF特征，并利用K-means算法聚类，得到K个聚类中心，每个聚类中心看作一个视觉单词，所有视觉单词构成一个大小为K×64的视觉词汇表Vdictionary=[v1,v2,...vk]。若聚类数K过小，则图像的SURF特征划分粗糙，导致视觉词汇的区分度低。而聚类数过大，容易造成信息冗余。所以本文将通过实验选取合适的K值。

得到视觉词汇表之后，将极片缺陷SURF特征按照最近邻原则D(Vi,Vsurf)=min{D(Vsurf，Vj)j=1,2,...k}映射到视觉词汇表中距离最近的视觉单词上，通过统计每个视觉单词出现的次数或频率建立词频直方图。进一步将极片缺陷图像以词频向量形式表示，且大小为1×K维。如式(3)所示：

其中fSn表示第n个视觉单词出现的次数。

2 极片缺陷灰度特征提取及特征融合

2.1 灰度特征提取

一般情况下，极片划痕缺陷由于光线原因会在缺陷处出现反光亮点，掉料缺陷区域比背景区域亮，暗斑缺陷区域较背景区域更暗。因此考虑从直方图中统计灰度参数信息，分析各极片缺陷的灰度分布。

以上灰度均值、方差和偏斜度的表达式中，L是灰度级数，P(ri)表示灰度值ri出现的概率。将这三个灰度参数分别用fh1，fh2，fh3表示并组合得到一个三维特征向量Fh，以此描述极片缺陷图像的灰度特征。如式(4)所示：

2.2 特征融合

SURF特征虽然对光照和噪声等因素具有鲁棒性，但只是针对局部的分析，缺乏极片缺陷的全局信息。而灰度特征从全局角度描述极片缺陷的灰度值分布，计算简单，但忽略了细节特征。将这两种特征融合可以互相弥补不足，从多方面描述极片缺陷，获取更丰富的信息。

在融合之前，采用min-max方法如式(5)所示分别对两种特征向量归一化，避免不同特征间的量纲差异对分类性能的影响。

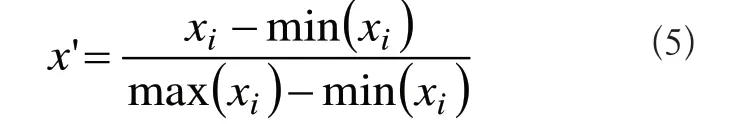
将归一化后的特征向量分别表示为F'BOF-SURF和F'h。

特征融合[11]指按照某种规则组合待融合的特征并得到新的特征，包括串行和加性融合方式。串行融合是直接将两个特征向量连接得到一个新的特征向量，且维度是待融合特征的维度之和。加性融合是将待融合的特征对应维度位置的元素相加，融合后特征向量的维度不变，这要求待融合特征的向量长度尽量相同。本文提取的特征向量F'BOF-SURF是K维，F'h是3维，两者维度差异较大，不适用加性融合。

因此尝试串行融合两种特征，并考虑到不同的特征对分类性能的重要程度不同，所以融合时对归一化后的特征加以相应的权值，得到融合特征V表示如下：

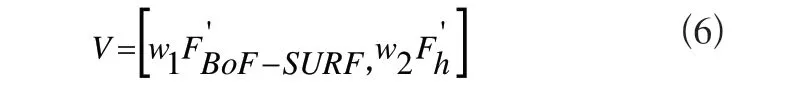
其中w1和w2分别是F'BOF-SURF和F'h的权值系数，且w1+w2=1。系数值将通过实验分析选取。

3 实验验证及结果分析

3.1 实验准备

为了验证特征融合方法对极片缺陷描述的有效性，结合分类算法对缺陷进行分类实验。实验样本的训练集和测试集各有255幅极片缺陷图像，其中包括划痕、掉料和暗斑三种缺陷。划痕缺陷是由硬物划伤所致；掉料缺陷是辊压压力过大导致；暗斑缺陷是异物或杂质导致。图1为极片缺陷图像。

图1 极片缺陷图像

由于本文的实验样本少，而SVM算法[12]对于小样本、非线性模式识别具有独特的优势，而且对未知样本具有较好的泛化能力，得到广泛应用。因此选择SVM算法结合融合特征对极片缺陷分类。在训练阶段，依据本文所提特征融合方法提取极片缺陷图像的特征向量，再将其输入SVM中训练并建立分类模型。在预测阶段，调用模型实现分类。图2为算法框架。

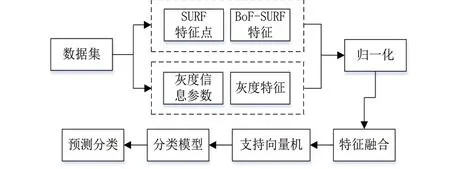
图2 本文算法框架

3.2 实验及结果分析

实验1 聚类数K的选择。经过1.2节分析可知，K值过大或过小均不利于缺陷的分类，因此本文选择在100～400之间，以增幅50选取不同的K值对SURF特征聚类，然后BoF量化得到特征向量，结合SVM算法对极片缺陷测试样本进行分类，图3为实验结果。

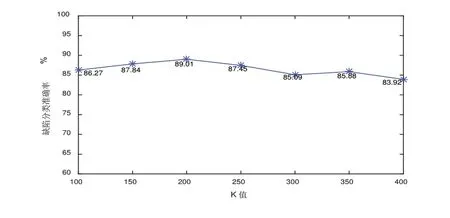
图3 不同K值下缺陷分类准确率

从图3分析可知，取不同K值是确实对分类性能有不同的影响。本文实验样本下K值为200时，极片缺陷的分类准确率最高。为进一步精确K值，在K取200附近继续缩小增幅范围，得出最佳K值为190，此时准确率为89.8%。

实验2 特征权值系数的确定。在实验1的基础上使用最佳K值，分析不同特征权值系数时本文算法的分类性能。如图4所示，横轴w1表示BoF-SURF权值系数，纵轴表示使用融合特征时的分类算法性能。w1=0表示只使用灰度特征的时分类准确率，w1=1表示只使用BoF-SURF特征时的分类准确率。w1在0和1之间时表示两种特征以不同的系数加权融合。

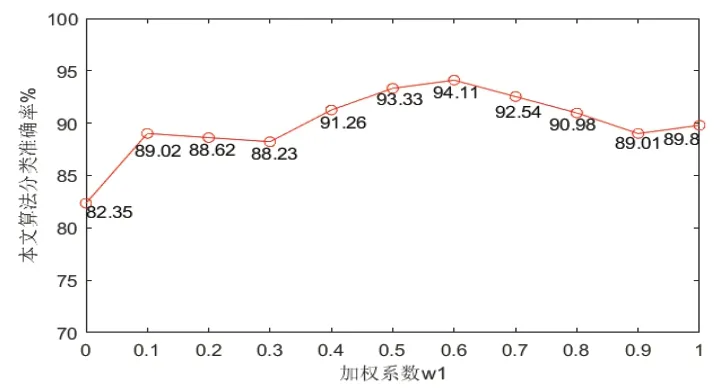
图4 不同加权系数下缺陷分类准确率

从图4分析可知，w1为0.6时本文算法取得最佳分类性能94.11%。而两种特征单独用于分类时，BoF-SURF的效果更好，因为局部特征更能反映本质特性。

实验3 分类算法时间性能比较。表1是SVM+Fh、SVM+FBOF-SURF和本文算法对单幅极片缺陷图像的平均分类时间。其中SVM+FBOF-SURF和本文算法所用K值为实验1所得最佳值，本文算法所用权值系数则是实验2所得最佳值。

表1 分类算法的时间性能比较

以上算法的时间性能差异主要体现在灰度特征易于计算和提取，FBOF-SURF特征需要聚类和量化处理，而本文算法分类时除了两种特征的提取，还要对其加权融合，所以单幅极片缺陷图像的平均分类时间最长。结合表1和图4可知，SVM+Fh分类算法时间性能最佳，但分类效果最差。而本文算法与SVM+FBOF-SURF算法相比，虽然在时间性能上相差不大，但是分类效果更好。综合以上分析，本文提出的特征融合与SVM算法对极片缺陷分类性能更好。

4 结语

为了对极片缺陷的描述更全面，从而提高分类性能，本文提出将BoF-SURF特征与灰度特征加权融合。为验证所提方法的有效性，结合SVM算法对极片缺陷进行分类实验，结果表明本文所提方法对极片缺陷的分类有较好的性能，准确率达94.11%。在后续工作中将继续研究其他融合方法，尝试更多类型缺陷分类。