400 km/h条件下现行路基过渡段设计标准适应性研究
2021-11-04周和祥李安洪
周和祥 李安洪 周 成 李 宁, 罗 强
(1.中铁二院工程集团有限责任公司, 成都 610031; 2.西南交通大学,成都 610031)
近年来,随着高速铁路技术的迅猛发展,高速化已成为当今铁路发展的主要方向之一[1-2],为铁路运输行业注入了新的动力。中国拥有目前世界上规模最大、运营速度最快的高速铁路网,截至2019年12月,运营总里程达3.5万 km,最高运营速度达350 km/h。积极开展400 km/h高速铁路相关研究,对我国高速铁路发展重要意义。
当列车运行速度提高至400 km/h后,轨面不平顺所引起的动力作用更大,并向上传导至车辆系统,向下传递至线下结构,作为轨道结构基础的路基基床的动力作用也相应被放大。同时,动力作用加大又会影响轨道结构部件疲劳破坏和线路变形累积,加剧轨道几何状态的恶化。在列车荷载长期作用下,路基与相邻结构的刚度差异使路基过渡段更易产生差异沉降,并通过轨道结构映射到钢轨,形成轨面几何不平顺,动力作用更为明显。
现行TB 10621-2014《高速铁路设计规范》对过渡段的相关规定适用于350 km/h的高速铁路,其在400 km/h技术条件下的适应性还有待研究。本文以沪渝蓉高速铁路重庆至成都段为依托,构建了车辆-轨道-路基耦合动力学模型,对400 km/h条件下的列车动力学性能开展研究,同时重点分析了轨面折角、路基刚度、列车运行方向等因素对列车动力学性能的影响,并对现行过渡段设计标准在400 km/h条件下的适用性进行了初判,研究成果可为今后400 km/h及更高速度高速铁路过渡段的设计提供有益参考。
1 动力学计算模型
1.1 模型参数
列车在轨道结构上运行,车辆系统、轨道系统与路基系统之间的动力影响与荷载作用是一个动态耦合的过程。轨面几何不平顺与轨下结构支承刚度变化引起的轮轨接触力是整个耦合系统产生振动的激励源,并向上传导至车辆系统,向下传导至轨道系统与路基系统[3]。传统拟静力路基结构设计方法与相应的动力系数限值应当与车辆-轨道-路基耦合系统的动态响应相适应,符合车辆-轨道-路基耦合动力学原理。随着列车运行速度的加快,耦合系统动力更加明显,在列车运行速度高达400 km/h的技术条件下,有必要对路基过渡段性能进行动力学评估。因此,本文采用车辆-轨道-路基耦合动力方法,建立大系统耦合模型,仿真分析车辆系统、轨道系统、路基系统的动力作用特点,分析路基过渡段结构动力响应,评价现有规范标准下的路基过渡段在400 km/h技术条件下的动力学性能。
基于耦合动力学原理,建立了车辆-板式无砟轨道-路基耦合动力学垂向模型。其中,车辆系统基于多刚体动力学抽象为多刚体弹簧阻尼系统[4],考虑到CR450高速铁路动车组尚在研发中,相关动力学参数还不明确,车辆采用CRH380A车;钢轨考虑其周期离散支承特点,抽象为离散支承Euler梁;针对CRTSⅢ型轨道板结构形式特点,将其抽象为连续支承条件下的单向自由板。
1.2 动力学计算方案
根据TB 10621-2014《高速铁路设计规范》[5]和TB 10001-2016《铁路路基设计规范》[6]要求,高速铁路无砟轨道过渡段长度不小于20 m。当过渡段长度较长时,过渡段材料与结构过渡会更加平缓,考虑最不利情况,过渡段长度取20 m。
路基过渡段差异沉降直接影响轨道的几何形位,进而导致轨面产生几何不平顺,以轨面高低不平顺为主,这种高低不平顺可采用轨面平折角来表示。
根据TB 10621-2014《高速铁路设计规范》和TB 10001-2016《铁路路基设计规范》要求,不均匀沉降造成的轨面平折角不应大于 1/1 000。
另外,耦合系统中的车辆系统考虑了向下重力作用的影响,此时“上坡”形式平折角与“下坡”形式平折角的动力作用分布形态与峰值点的出现位置存在明显差异,如图1、图2所示。因此,两种情况应分别加以考虑。

图1 上坡平折角轨面不平顺示意图

图2 下坡平折角轨面不平顺示意图
线路纵向不同结构因材料性质与结构特点造成的刚度差异是产生过渡段问题的原因之一。刚度差异的影响主要体现在两个方面,一是在列车荷载长期反复作用下,线路纵向会产生沉降差异,映射至钢轨,产生轨面几何不平顺;二是在列车运行中直接影响车辆-轨道-路基耦合系统的动力响应。
路基基床结构常采用地基系数K30控制,根据TB 10621-2014《高速铁路设计规范》及TB 10001-2016《铁路路基设计规范》中关于高速铁路无砟轨道路基压实控制指标的相关规定,基床表层地基系数K30≥190 MPa;基床底层采用粗砾土、碎石类土时,地基系数K30≥150 MPa,采用砂类土(粉砂除外)、细砾土时地基系数K30≥130 MPa;基床以下路堤采用粗砾土、碎石类土时,地基系数K30≥130 MPa,采用砂类土、细砾土时,地基系数K30≥110 MPa。一般认为基床结构的弹性模量与地基系数K30在数值上大致相当[7]。
E/(MPa)=K30/(MPa/m)
(1)
由此可知,路基结构与混凝土结构在模量相差约两个数量级,即支撑刚度相差约100倍。考虑过渡段范围内,路基支撑刚度线性过渡,即当路基向其他结构物过渡时,路基刚度在刚度过渡区间内由Kf线性增加至100Kf(如图3所示),而其他结构物向路基过渡时,路基刚度在刚度过渡区间内由100Kf线性减小至Kf(如图4所示)。

图3 路基-其他结构支撑刚度过渡示意图

图4 其他结构-路基支撑刚度过渡示意图
过渡段处车辆-轨道-路基耦合系统动力学响应受到列车运行速度、轨面平折角、路基支撑刚度及行车方向等因素的综合影响,车辆-轨道-路基耦合动力学计算分析时应充分考虑这些因素。
过渡段长20 m时,对列车运行速度400 km/h与350 km/h、轨面平折角考虑0‰与1‰、路基相邻结构与路基支撑刚度倍数考虑1倍(即路基支撑刚度不变)与100倍、列车运行方向考虑“上坡”与“下坡”等工况进行合理组合,共考虑12种计算工况,其中工况1-1~工况1-6为列车运行速度350 km/h条件下不同轨面平折角、支撑刚度比与行车方向的组合,工况2-1~工况2-6为列车运行速度400 km/h条件下不同轨面平折角、支撑刚度比与运行方向的组合,如表1所示。
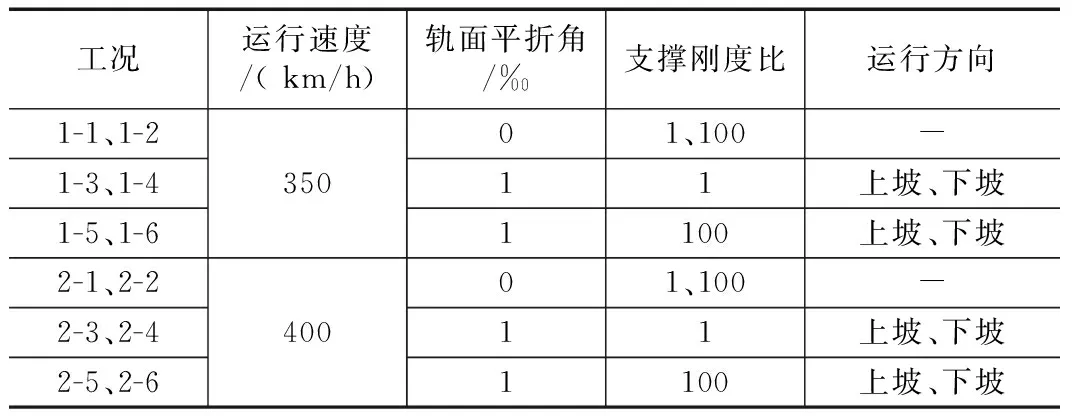
表1 过渡段耦合动力学计算方案表
2 动力学性能评价指标与仿真结果
2.1 动力学性能评价指标
从车辆运行安全性、车辆运行平稳性、车辆与轨道动态作用性能三方面评价各计算工况下车辆-轨道-路基耦合系统的动力学性能[8]。
(1)安全性评价标准
根据铁运[2008]28号关于印发《高速动车组整车试验规范》的通知[9]要求,对于最高运行速度200 km/h及以上的电力动车组,其轮重减载率执行标准为:
(2)
(2)车辆运行平稳性评价标准
TG/GW 115-2012《高速铁路无砟轨道线路维修规则》[10]按照不同速度等级及养护维修标准将轨道动态不平顺管理值偏差等级划分为Ⅰ~Ⅳ级,并对相应的线路轨道动态质量容许偏差管理值进行了规定,对于350 km/h的无砟轨道线路,在经常保养水平下(即偏差等级为I级),车体垂向加速度的容许偏差管理值为1 m/s2。
(3)车辆与轨道动态作用性能评价标准
《高速动车组整车试验规范》规定最高运行速度200 km/h以上的电动车组,其轮轨垂向力最大限制值为170 kN。
2.2 动力学仿真计算结果
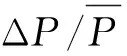
(1)速度因素影响
相比350 km/h运行速度,当列车运行速度提升至400 km/h时,大部分工况的车体垂向加速度、轮轨力、轮重减载率等指标均有所增加,表明动力作用增大,如表2所示。其中工况1-1、2-1、1-2、2-2因未设置轨面平折角,其动力学指标相对其他工况均较小,因此增幅有减小或较大的情况,而在其他工况中,车体垂向加速度增幅为7.4%~8.6%,轮轨力增幅为4.9%~5.8%,轮重减载率增幅为11.1%~12.2%,轮重减载率的增幅最大。

表2 350 km/h与400 km/h条件下动力学指标增幅表
(2)刚度因素影响
不同路基支撑刚度情况下的动力学指标增幅如表3所示。

表3 路基支撑刚度倍数k变化的动力学指标增幅表
从表3可以看出,路基支撑刚度变化对动力学计算指标影响很小,其中工况1-1、工况2-1、工况1-2、工况2-2因未设置轨面不平顺,其动力学指标相对其他工况均较小,因此增幅有减小或较大的情况,而在其他工况中,车体垂向加速度增幅为0.4%~1.5%,轮轨力增幅为0~0.5%,轮重减载率增幅为-2.8%~-1.2%,车体垂向加速度与轮轨力均增加,轮重减载率减小,轮重减载率的变化幅度最大,但仍未超过3%。工程中,一般认为5%为是否存在影响的界限,因此可认为是否存在长度为20 m的刚度由Kf线性变为100Kf或由Kf线性变为100Kf的刚度渐变段对垂体垂向加速度、轮轨力、轮重减载率影响均不大。
(3)折角不平顺及列车运行方向因素影响
不同轨面不平顺条件下的动力学指标如表4所示。

表4 不同轨面不平顺条件下的动力学指标表
从表4可以看出,是否设置轨面折角不平顺对系统的动力学性能影响显著,折角不平顺设置为上坡型或下坡型对动力响应也有影响,但影响程度不及是否设置轨面折角不平顺明显。未设置轨面不平顺的车体垂向加速度约为0.01 m/s2,设置1‰上坡平折角不平顺的车体垂向加速度在0.26~0.28 m/s2之间,较设置1‰下坡平折角不平顺的车体垂向加速度(在0.24~0.26 m/s2之间)大,两者相差约0.02 m/s2,约为8.2%。未设置轨面不平顺的轮轨力约为70 kN,设置1‰上坡平折角不平顺的轮轨力在106~112 kN之间,较设置1‰下坡平折角不平顺的轮轨力(在103~109之间)大,两者相差约2 kN,约为1.9%。未设置轨面不平顺的轮重减载率约为0.01,设置1‰上坡平折角不平顺的轮重减载率在0.43~0.50之间,较设置1‰下坡平折角不平顺的轮重减载率小,两者相差约0.03,约为6.9%。
2.3 动力学性能对比评价
当列车运行速度由350 km/h提升至400 km/h时,三项动力学指标均增大,但都未超过限制值,现有路基过渡段结构在400 km/h条件下仍具有适应性。在车体垂向加速度、轮轨力、轮重减载率三项控制指标中,轮重减载率最接近控制值,其次是轮轨力,车体垂向加速度远小于控制值,如表5所示。
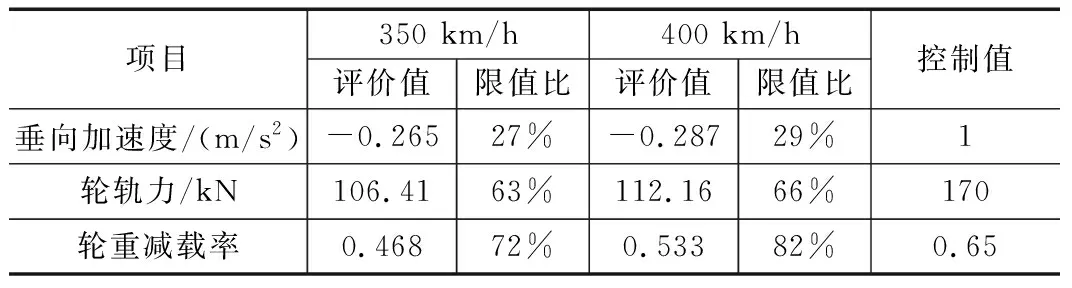
表5 不同时速条件下动动力学评价指标对照表
3 结论
本文针对现行路基过渡段设计标准在400 km/h条件下的适应性问题,开展了动力学仿真分析,得出以下主要结论:
(1)过渡段支撑刚度变化对过渡段动力学性能影响不大;轨面不平顺对过渡段动力学性能影响显著。在设计施工过程中,当过渡段差异沉降不能满足轨面平折角控制指标要求时,应采取必要的工程措施以确保列车安全、平稳通过。
(2)当列车运行速度由350 km/h提升至400 km/h时,三项动力学指标均增大,但均未超过限制值,现有路基过渡段结构在400 km/h条件下仍具有适应性。在车体垂向加速度、轮轨力、轮重减载率三项控制指标中,轮重减载率最接近控制值,其次是轮轨力,车体垂向加速度远小于控制值。
(3)短路基平顺过渡是目前铁路路基设计与施工面临的重点问题,后续还应进一步开展短路基过渡段的研究。
