相对论下的钟慢效应公式推导及其应用

王 勇 朱小芹 唐 煌

（1.江苏省常州高级中学，江苏 常州 213003；2.江苏理工学院数理学院，江苏 常州 213001）

1905年，爱因斯坦发表了狭义相对论的第一篇论文《论动体的电动力学》，提出了狭义相对论的两个基本原理.

（1）相对性原理：物理定律在所有惯性系中都是相同的，所有的惯性系都是等价的.

（2）光速不变原理：在所有惯性系中，真空中光速等于恒定值，它不依赖惯性系之间的运动，也与光源、观察者的运动无关.

经典时空观认为时间和空间是两个独立的观念，彼此之间没有联系，分别具有绝对性，时间与空间的度量与惯性参考系的运动状态无关.

爱因斯坦相对论时空观认为：空间和时间的特性是相对的，是随着物质运动状态的变化而变化的，并不是永恒不变的.

1 钟慢效应公式推导

在相对论时空观中，运动的时钟比静止的时钟走得慢，这种效应叫做时间延缓或时间膨胀，也叫钟慢效应，钟慢效应公式推导过程如下.

图1

假定列车（惯性系S′）以速度v相对路基行驶.车厢后壁装有光源，紧挨着它有一标准钟，在对面放置一面反射镜M，可使纵向发射的光脉冲原路返回，设车厢宽度为l0.

2 钟慢效应的应用

例题.惯性系S中3艘已处于匀速直线运动状态的飞船1、2、3，各自的速度大小同为v，航向已在图中标出.某时刻3艘飞船“相聚”（彼此靠近，但不相碰）于S系的O点.此时各自时钟都校准在零点.飞船1到达图中与O点相距l的P处时，发出两束无线电信号.而后分别被飞船2、3接受到.

图2

（1）在飞船1中确定发射信号的时刻t1；

（2）在飞船2中确定接收信号的时刻t2；

（3）在飞船3中确定接收信号的时刻t3.

解析：（1）S系中飞船1从O点到达P点所经过的时间为，飞船1中发射信号的时刻为飞船1从出发到发射信号的时间，两事件在飞船1中为发生在同一地点的两事件，此经历的时间是本征时间，本征时间与S系中飞船1从O点到达P点所经过的时间关系为，其中（下同），所以飞船1中发射信号的时刻为

（2）方法1：在惯性S系中讨论.

在S系中飞船1发射信号后相当于光追飞船2，则在S系中飞船2从相聚点出发到收到信号的时间为

所以根据钟慢效应，飞船2中接受到信号的时刻为

将（7）式代入（8）式可得飞船2中确定接收信号的时刻为

方法2：在惯性系飞船2中讨论.

由速度变换公式可得1相对2的远离的速度为

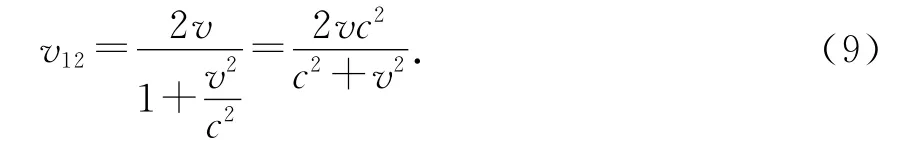
在惯性系飞船2中，飞船1从出发到发射信号的本征时间为

在惯性系飞船2中，飞船1从出发到发射信号用了

将（9）、（10）式代入（11）式可得

在惯性系飞船2中，飞船2认为飞船1走了v12Δt2才发射信号.从飞船1发射到飞船2接收信号用了时间

将（9）、（12）式代入（13）式可得

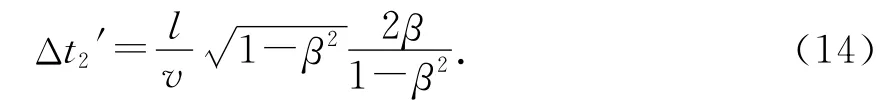
飞船2中接受到信号的时刻为

将（12）、（14）式代入（15）式可得

方法3：在惯性系飞船1中讨论.

由速度变换公式可得2相对1的远离的速度为

飞船1从出发到发射信号的本征时间为

此时飞船1系中观察者认为飞船2前进了v21Δt1，则从1发出信号到2接收信号，相当于光追及飞船2，飞船1发出的信号到飞船2接受到信号经过时间为

从相聚点到飞船2接收到信号，飞船1系中共经过了

将（17）-（19）式代入（20）式可得

变换回2系，惯性系飞船2中的为本征时间为

将（21）式代入（22）式可得

问题（3）：（3）问中分析飞船3中确定接收信号的时刻时，只需通过相对论下速度变换公式分别对x方向、y方向的速度变换，飞船1将相对于飞船3斜向运动，相对速度为，参照问题（2）的解答只需将飞船1与飞船2间的相对速度v12变换为飞船1与飞船3的相对速度v13即可求解可得

在狭义相对论的时空观中，运动的时钟走慢.利用动钟变慢公式，变换参考系分析相对论下的时钟问题，充分锻炼学生的思维能力，使学生从不同的角度对钟慢效应进行思考，深入理解狭义相对论的时空观.