基于MPS法的齿轮啮合区不同浸油程度下搅油损失仿真分析*

2021-11-04王交龙吕红明

润滑与密封 2021年9期

王交龙王斌吕红明宁斌

(1.江苏大学机械工程学院江苏镇江 212000；2.盐城工学院机械工程学院江苏盐城 224051；3.上海海洋大学工程学院上海 201306)

降低齿轮搅油功耗一直是机械传动领域难以突破的问题，也是流体动力学领域研究的热点和难点。CFD(Computational Fluid Dynamics)是常用的流体分析法，可分为无网格法与有网格法。在分析减速箱齿轮搅油产生的大变形自由液面问题时，有网格法总显得捉襟见肘。移动粒子半隐式法(Moving-Particle Semi-implicit Method,MPS)是近些年流行的一种基于拉格朗日(Lagrange)的无网格粒子法，最早由KOSHIZUKA和OKA[1]在1995年提出，用于求解大变形自由液面流体力学问题。MPS法具有粒子运动自由、可观测、可量化等特点，在模拟大变形的自由表面上拥有卓越的计算分析能力。与网格法不同，MPS法将流体离散为一系列具有物理属性的微小粒子，通过了解粒子的属性从而掌握整个流域的动态。

虽然MPS法提出时间相对较短，但已被应用于许多研究领域。KHAYYER和GOTOH[2-3]对MPS法进行了改进，将高阶拉普拉斯的算子形式引入到MPS法，并通过模拟晃荡问题来验证该方法对增强初始MPS方法计算压力的稳定性和有效性。TANAKA和MASUNAGA[4]同样着力于利用MPS法解析流体压力稳定性和光滑性方面的研究，模拟仿真不可压缩流体溃坝模型。2005年前后，国内学者开始关注MPS法并展开相关研究。段日强等[5]使用MPS法进行多相多组分界面流模拟分析，验证了该方法在处理复杂流相流体的强大计算能力。周雅杰等[6]建立了齿轮箱内流域有限元模型，采用VOF两相流理论与SIMPLE算法并应用该模型考察齿轮圆周面、啮合区油液的流态变化，计算齿轮搅油损失值。尹志敏和刘少军[7]采用Flowmaster仿真方法，建立某型直升机主减速器润滑系统喷嘴的仿真模型，以供油压力为单一变量对模型进仿真研究，验证该仿真方法准确性。孙凯等人[8]应用Fluent软件对飞溅润滑的非正交螺旋锥齿轮中减速器内部流场进行动态数值仿真分析。皮彪等人[9]成功将MPS法运用到重型汽车减速器润滑分析中，并优化了减速器润滑效果。姜义尧等[10]基于CFD，运用VOF多相流模型和湍流模型建立了减速器润滑仿真模型，分析了转速与浸油深度对润滑油流量的影响并进行了实验验证。傅志红等[11]基于MPS法对减速器内的油流进行了数值模拟，研究了油位、转速对减速器润滑的影响规律。DENG等[12]采用MPS法对高速列车齿轮箱内流场进行数值模拟，分析了高速运行时齿轮箱内的润滑机制。

MPS法自问世以来，因其计算简便、计算性能高效、信息采集便捷等特点，在许多领域饱受关注。本文作者将MPS法应用于减速箱搅油损失研究领域，采用MPS法对齿轮搅油模型进行模拟分析，研究啮合区浸油程度对齿轮搅油损失的影响规律。

1 基于异构箱体的齿轮搅油损失仿真分析

CHEN和MATSUMOTO[13]对8种异构齿轮减速箱进行了搅油实验。该实验具有典型性和代表性，因此文中应用MPS粒子法模拟该实验条件，应用MPS粒子法对不同结构的减速箱齿轮搅油损失进行仿真分析，并从速度、流态、搅油损失三方面对仿真结果进行分析，探究齿轮箱体结构对齿轮搅油损失的影响。

1.1 减速箱结构及仿真条件

文中对文献[13]中8种异构齿轮减速箱进行模拟仿真，齿轮参数和实验条件如表1所示，润滑油参数如表2所示，实验减速箱结构如图1—3所示。α与β的具体定义如图1所示，图2、3中，插入b类木板，木板表面与齿轮下齿顶点的距离，与插入T类木板，木板内壁至齿轮齿顶圆直径距离均用L表示。

表1 齿轮参数和测试条件Table 1 Gear parameters and test conditions

表2 润滑油参数Table 2 Lubricating oil parameters

图1 α、β角度示意Fig 1 Shcematic of α,β angles

图2 插入b类木板结构Fig 2 Structure of inserting b class plank

图3 插入T类木板结构Fig 3 Structure of inserting T class plank

1.2 仿真模型的建立

对VG320、β=180°、α=90°条件下的搅油实验模型进行仿真，并对比实验结果来验证MPS法的准确性。根据实验模型，使用NX进行齿轮箱三维建模，确保模型参数与文献[13]相一致。齿轮参数如表1所示，箱体参数如图4所示。

图4 粒子生成示意Fig 4 Schematic of particle generation

在齿轮搅油功率损失中，轴类零件功率损失比重仅次于齿轮搅油损失。为除去轴承及轴类密封件损失的影响，进一步保证仿真结果的可靠性，在NX中采用布尔运算去除传动轴及其附属部件，对箱体内部进行简化，只保留齿轮副与相关木板。如图4所示，齿轮箱三维模型内部尺寸为长144 mm、宽49 mm、高224 mm。由于齿轮箱相对水平位置旋转了90°，所以长宽高等齿轮参数也对应变化。

1.3 MPS前处理设置

1.3.1 模型参数设置

在MPS法软件中导入仿真模型文件后需对其进行前处理设置。首先需要定义箱体、齿轮、液面的物理属性。箱体与齿轮作为实体与润滑油直接接触，因此将箱体定义为Polygon(多面体)，Polygon作为实体的一种，无法设置固体密度等参数。将齿轮定义为Solid(固体)，Solid也为实体类型，但可以定义固体的密度、热导率等参数。将润滑油定义为Fluid(液体)，润滑油类型为表2中VG320型油液，设置密度为887.3 kg/m3，运动黏度为305.3 mm2/s。由于液体存在张力，因此设定液体张力系数为0.072，液体定义为牛顿流体，其余参数不变。

1.3.2 液体粒子参数设置

在物理模型中生成液体粒子，需要确定液体生成起始面、粒子大小、液体密度和张力等参数。该实验条件下液体生成起始面相对箱体底面的高度为77 mm，为保证液体粒子顺利生成，液体重心不应与齿轮等固体模型重合，即液体中心在Y轴方向移动一定距离。其次，为保证仿真结果的有效性与观测良好性，需要确定粒子生成数目应在100万～150万之间。因此在一定空间的箱体内确保粒子生成数目，则需要相应改变粒子体积，确定粒子半径为0.7～0.8 mm之间，如图5所示。

图5 粒子参数Fig 5 Particle parameters

1.3.3 液体压力与湍流设置

设置液体重力方向为Z轴负方向，对压力与黏度进行软件Implicit(隐式)求解。压力项通过方程(1)获得，该方程是通过将压力稳定模型与包含压缩系数a和松弛系数λrat压力部分合并而创建的，将无量纲常数b和r的值设为1。当用压力方程计算压力时，当时间间隔因动态条件或其他条件而波动时，往往会出现严重的压力振荡，因此需要建立dt独立模型。由于齿轮搅油模型为单相流体模型，因此采用连续介质模型(CSF)来计算表面张力。具体设置如图6所示。

图6 压力、黏度、张力、湍流设置Fig 6 Setting of pressure,viscosity,tension and turbulence

(1)

1.3.4 时间步长设置

在仿真过程中，为了提高计算精度，通过添加Courant限制器来使一些速度较大的粒子减速，使它满足CFL条件。式(2)为CFL计算收敛条件，初始时间步长设置为2×10-5s，输出时间间隔为0.001 s。

(2)

式中:C为柯朗数，取值0.2；l0为粒子直径；umax为粒子最大速度。

前处理设置完成后，初始状态的齿轮箱模型如图7所示。箱体为无网格流体仿真的固体边界条件，粒子代表润滑油，具有润滑油的物质属性。

图7 齿轮箱仿真模型Fig 7 Simulation model of gearbox

1.4 仿真结果对比分析

MPS仿真分析法以时间步长为基础，分析不同时刻瞬态下流体的流态、油液与速度分布。文中通过MPS法对VG320、Ω=1 500 r/min，β=180°工况下8种实例进行模拟仿真，同时将仿真搅油损失数据与实验数据进行对比，验证MPS法的有效性与准确性。

文献[13]齿轮搅油实验结果如图8所示。从速度矢量方面分析，油液速度分为齿轮区速度与齿外区速度；齿轮区速度又分为齿周面区(齿牙区)速度与齿端面区速度。根据纳维-斯托克斯黏性流体边界条件，必须满足固体不滑移条件，即速度连续性条件。当固壁以速度vw运动时，固壁上流体的速度：v=vw；当固壁静止时，固壁上的流体也静止。如图9所示，齿牙区流体速度与齿牙线速度相近，因此齿牙区粒子速度最高；箱体壁面静止不动，速度为0，因此靠近箱体壁面粒子的速度为0。以齿轮为中心，粒子的速度由高至低扩散，速度分布符合牛顿黏性流体速度连续性条件。

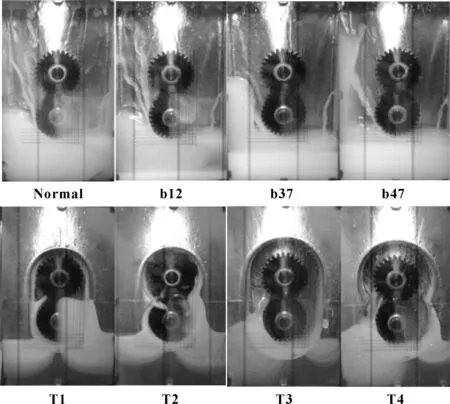
图8 齿轮搅油实验结果[13]Fig 8 Gear oil mixing test results[13]

图9 齿轮搅油仿真结果Fig 9 Simulation results of gear oil mixing

从油液分布方面分析，齿轮转向为顺时针，因此油液由于齿轮的带动都集中在箱体的左侧，在b类木板实例中，在齿轮浸油程度不变的情况下，随着所加木板厚度的增高，润滑油初始体积V0减少，润滑油的波动越剧烈，油液飞溅高度越高；在T类木板实例中，油液受到木板形状的限制，在与齿轮圆周间距相等的情况下，T2类木板相较于T1类木板油液更容易到达啮合区；在木板形状形同的情况下，T3类木板相较于T1类木板间距更小，油液更容易到达啮合区。对比仿真结果与实验结果，油液分布基本一致。

综上所述，采用MPS法对齿轮搅油的仿真结果与实验结果一致，在后续齿轮搅油损失影响因素研究中可采用该方法。

2 不同浸油程度的搅油损失仿真分析

2.1 齿轮搅油损失的研究理论

齿轮搅油损失分为有负载损失与无负载损失，无负载损失占比较大，各影响参数彼此关联但关系复杂，难以准确测量。无负载损失又可分为齿轮阻力损失(齿轮与油液摩擦的损失与风阻损失)，齿轮啮合损失(齿轮啮合区吸油与挤压油所造成的损失)，气泡损失(搅油时产生的气泡所造成的能量损失)。

CHANGENET和VELEX[14]关于雷诺数Rec<4 000工况下的搅油经验公式为

(3)

式中:Cch为单个齿轮的齿轮扭矩损失；Sm为单个齿轮的浸油总面积(包括齿轮端面与齿轮周面的面积)；rp为齿轮节圆半径；Ω为齿轮转速；Cm为齿轮扭矩损失系数，是一个无量纲量,其表达式如下：

(4)

式中：H为浸油程度；V0为油液的初始体积。

由式(3)(4)可知，齿轮扭矩损失与V0成正比。

CHEN和MATSUMOTO[13]指出两式中扭矩损失随V0增加且无上限具有局限性，进而推论：油液深度在达到啮合区之前，齿轮啮合区已被油液充满。但考虑到实际工况下，浸油程度不会超过中心轴，所进行的实验中浸油程度都未达到齿轮啮合区，并未对浸油程度达到齿轮啮合区及浸没啮合区后的情况进行实验研究与分析。

随着浸油程度缓慢到达啮合区并浸没啮合区的过程中，由于油液的影响，齿轮阻力损失Td与齿轮啮合损失Tt必定会有所变化，两者与齿轮总损失之间的关系也会改变。因此，为探究齿轮副啮合区浸没程度对齿轮啮合损失及其与齿轮阻力损失关系的影响，文中利用MPS法对不同油位、插入不同特殊木板的工况进行仿真分析。

2.2 仿真条件

上文已经验证模型b25仿真数据与实验数据是一致的，为保证仿真模型的可靠度，仿真分析选用模型b25。齿轮箱体参数如图4所示，仿真参数如表3所示。

表3 仿真参数Table 3 Simulation parameters

为测量齿轮副啮合区域范围，建立了齿轮啮合模型，如10(a)所示，齿轮副初始啮合点A与终止啮合点B的竖直距离为16 mm，且相对于齿轮副中心线对称。如图10(b)所示，为将齿轮啮合区完全包围，取仿真模型油液范围为24 mm，分为4等份。

图10 油液深度示意Fig 10 Schematic of oil depth diagram

表3中S为油液深度，H为液面高度，s表示仿真模型油液范围每等份的距离6 mm，n表示中心线为起始，上下各分2等份，用数字1、2表示，+表示中心线以上，-表示中心线以下。齿轮转速Ω=±1 500 r/min，+代表主动轮顺时针旋转，-代表主动轮逆时针旋转，具体如图11所示。

图11 仿真油液生成Fig 11 Simulated oil generation

如图10所示，液面以啮合齿轮中心线(7 mm)对称分布。中心线高度h=77 mm，木板厚度B=25 mm，则液面高度H=h+n×s，即仿真设置液面高度H=77+n×s。仿真生成的油液深度S=h+n×s-B，即仿真生成的油液深度S=77+n×s-25。

2.3 仿真前处理

对模型进行前处理设置，b25模型相对水平位置并无旋转，因此长宽高的位置与图11模型稍有不同，但尺寸及齿轮箱参数均与上文相同。除主动轮旋转分为顺逆时针方向、油液深度改变之外，模型物理属性及前处理等其余设定与上文完全一致，最终生成的仿真模型如图12所示。

图12 仿真模型Fig 12 Simulation model

2.4 仿真结果及分析

在采用VG320型润滑油、齿轮转速±1 500 r/min条件下，通过分析速度与油液分布，不同时刻下齿轮啮合区润滑油浸没程度及变化，探究转向及啮合区浸油比例对搅油功率的影响特性。

在齿轮旋转4～5圈后齿轮搅油处于稳定状态，仿真设置齿轮转速为1 500 r/min，则在0.2 s以后搅油齿轮处于稳定状态。因此使用MPS法仿真，对齿轮搅油仿真环境逐帧观察，分别取6帧(0.06 s)、15帧(0.15 s)、27帧(0.27 s)时刻下的搅油状态进行分析，如图13—18所示。

在油液分布方面，如图13所示，在H=65 mm、转速为-1 500 r/min下，6～27帧时段内，随着齿轮旋转，油液由于齿轮搅动向箱体两侧与上方运动聚积，齿轮浸油程度逐渐减小。如图15、17所示，在H=77 mm与H=89 mm且其余参数不变条件下，稳定状态时刻前(6帧、15帧)，齿轮浸油程度S会随H增大而增大，但稳定状态下(27帧)齿轮浸油程度S并不随着H增大而变化；而箱体两侧与上方聚积的油液随H增大而增多，齿轮圆周处所带动的油液也随之增加。如图14所示，在H=65 mm、转速为+1 500 r/min条件下，油液随齿轮转动充斥齿轮啮合区，一部分从齿轮端面啮合区处挤压出来，另一部分被齿轮带动到箱体上方并落下。如图16、18所示，在H=77 mm与H=89 mm且其余参数不变条件下，齿轮浸油程度S变化较小，但齿轮啮合区挤油量随H的增大而增加，聚积在箱体上方的油液也随之增加；随着H的增大，箱体上方落下的油液增加，齿轮圆周处搅动的油液量也随之增加。

图13 H=65 mm，Ω=-1 500 r/min 瞬时速度分布Fig 13 Instantaneous velocity distribution at H=65 mm，Ω=-1 500 r/min (a) 6 frames (0.06 s);(b) 15 frames (0.15 s);(c) 27 frames (0.27 s)

图14 H=65 mm，Ω=+1 500 r/min 瞬时速度分布Fig 14 Instantaneous velocity distribution at H=65 mm，Ω=+1 500 r/min(a) 6 frames (0.06 s);(b) 15 frames (0.15 s);(c) 27 frames (0.27 s)

图15 H=77 mm，Ω=-1 500 r/min 瞬时速度分布Fig 15 Instantaneous velocity distribution at H=77 mm，Ω=-1 500 r/min(a) 6 frames (0.06 s);(b) 15 frames (0.15 s);(c) 27 frames (0.27 s)

图16 H=77 mm，Ω=+1 500 r/min 瞬时速度分布Fig 16 Instantaneous velocity distribution at H=77 mm，Ω=+1 500 r/min(a) 6 frames (0.06 s);(b) 15 frames (0.15 s);(c) 27 frames (0.27 s)

在速度分布方面，围绕在齿轮上及齿轮周边的油液速度最高且接近齿轮转速。齿轮与油液接触点切向油液的速度与齿轮转速相近，与箱体壁接触的油液静止且趋向箱体壁速度逐渐减小直至静止，符合上节中的速度连续性条件。随着浸油高度H的增加，油液速度分布愈发紊乱。

图17 H=89 mm，Ω=-1 500 r/min 瞬时速度分布Fig 17 Instantaneous velocity distribution at H=89 mm，Ω=-1 500 r/min(a) 6 frames (0.06 s);(b) 15 frames (0.15 s);(c) 27 frames (0.27 s)

图18 H=89 mm，Ω=+1 500 r/min 瞬时速度分布Fig 18 Instantaneous velocity distribution at H=89 mm，Ω=+1 500 r/min(a) 6 frames (0.06 s);(b) 15 frames (0.15 s);(c) 27 frames (0.27 s)

在齿轮搅油损失方面，如图19所示，齿轮的搅油损失随着浸油高度H的增加而增加。在1 500 r/min条件下，主动轮逆时针旋转的搅油损失小于主动轮顺时针的搅油损失；随着浸油高度H的增加，两者的搅油损失都在增大，但二者间的差距也逐渐增大。因为主动轮逆时针条件下，由于齿轮转向油液被甩到箱体两侧，少有油液进入啮合区域，此时只存在齿轮阻力损失Td，无齿轮啮合损失Tt。但随着齿轮浸油高度H的增加，齿轮圆周处带动的油液会逐渐增加并且聚积于箱体上方的油液变多，导致落入啮合区的油液增多，因此产生齿轮啮合损失Tt且随着H的增大而增加，齿轮搅油损失增加。在主动轮顺时针条件下，由于齿轮转向油液会瞬间充满啮合区，这与浸油高度无关。但随着浸油高度H增大，经过啮合区的油液量增多，齿轮带动到箱体上方的油液增多，落到齿轮圆周面的油液增大，此时齿轮阻力损失Td也随之增加；油液经过啮合区的油液增加，经啮合区挤压反映在箱体侧壁的油液量也随之增多，齿轮啮合损失Tt增大，齿轮搅油损失增加。但由齿轮转动聚积在箱体上方的油液量远比油液初始体积增量少得多，所以随着浸油高度H的增大，顺时针与逆时针搅油扭矩损失之差会逐渐增大。

图19 Ω=1 500 r/min 条件下顺逆转向搅油损失随浸油高度的变化Fig 19 Variation of churning oil loss of forward and reverse steering with oil immersion height under the condition of 1 500 r/min