如何正确运用χ2检验——生存资料的三种特殊检验与SAS实现

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在对生存资料进行假设检验时，除了在试验因素各水平组之间采取似然比检验和六种非参数检验之外，还有三种特殊的检验，即“多重比较”“趋势检验”和“协变量检验”［1］。这些假设检验方法在本质上都属于“χ2检验”。本文将详细介绍前述提及的三种特殊检验的计算公式，结合实例并借助SAS软件实现统计计算。

1 多组生存函数之间的多重比较

1.1 何为多重比较

设有K（K＞2）组生存函数，若同时对它们进行比较，就叫做整体比较；若每次仅取出两组进行比较，并按以下两种情形之一完成全部比较，就称为多重比较：情形一，任何两组生存函数之间都要进行一次比较，若K=4，总共需要比较6次；情形二，选定一个对照组，其他组都与此对照组进行比较，若K=4，总共需要比较3次。

1.2 多重比较的校正

1.2.1 校正的必要性

当需要对K（K＞2）组生存函数进行多重比较时，基于前述提及的两种情形，都至少需要比较2次。若每次比较都设定检验水准为α（通常设α=0.05），设总共需要比较m次，m的计算公式如下：

于是，m次比较所对应的犯I类错误的总概率PT就会大于α，其计算方法［1］如下：

PT=1-（1-α）m

例如，当m=6、α=0.05时，PT=0.264908＞0.05。

为此，需要对每次比较所得的概率P值进行校正，以保证整个多重比较所对应的犯I类错误的总概率PT小于等于α。

1.2.2 校正方法的种类

在 SAS/STAT 的“LIFETEST”过程中［1］，基于不同的统计学原理，对多重比较结果进行概率校正的方法有如下几种：Bonferroni校正法、Dunnett-Hsu校正法、Scheffé校正法、Šidák校正法、SMM校正法和Tukey校正法。

1.2.3 多重比较中变量的定义

1.2.4 多重比较中每次比较的共同检验统计量

将第j组与第l组中生存函数进行双侧检验所对应的检验统计量按下式计算：

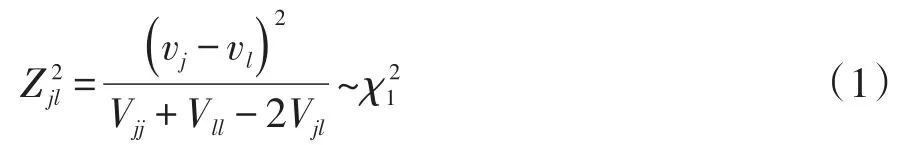
直接计算出来的P值（也称为原始P值）由下式计算：

1.2.5 多重比较中六种校正P值的计算公式

Bonferroni校正法计算P值的公式如下：

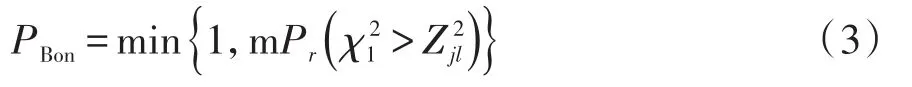
Dunnett-Hsu校正法计算P值的公式如下：

设以第一组为对照组，让C=（cij）代表（r-1）×（r）阶对比矩阵，即：

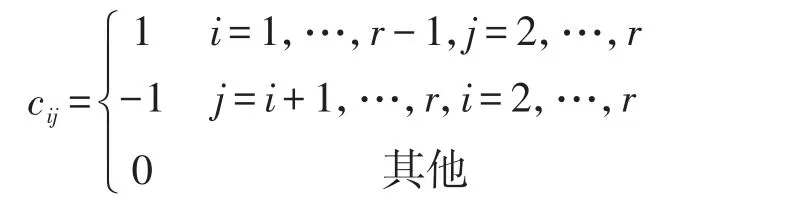
让∑≡(σij)与R≡(rij)分别代表矩阵Cv的协方差矩阵与相关矩阵，即：

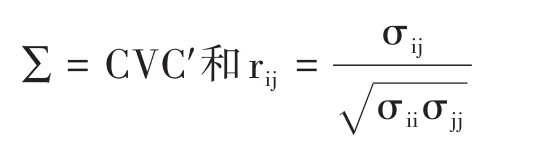
【说明】此处涉及“v”与“V”，V是v的方差。v和V的计算比较复杂，将在下文详细介绍。

于是，Hsu于1992年提出，从因子分解的协方差中近似求出λ1，λ2，…，λr-1，从而构造出以下方程式：

R=D+ λλ'

这里，D是一个对角矩阵，其对角线上第j个元素为1-λj，而且，λ =(λ1，λ2，…，λ)'。于是，校正r-1的P值可通过下式计算：

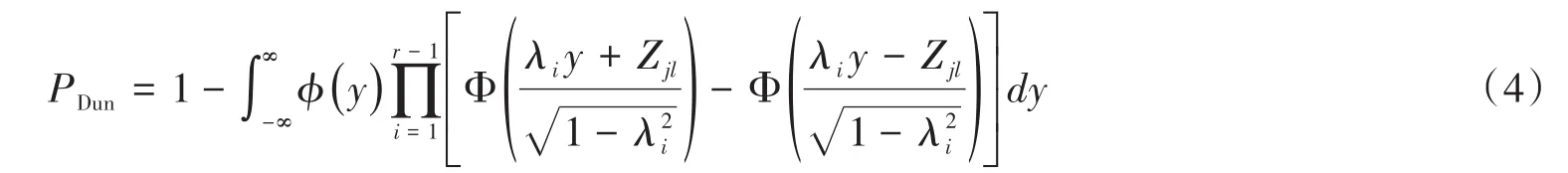
采用 Scheffé校正法、Šidák 校正法、SMM 校正法、Tukey校正法计算P值的公式分别见式（5）、式（6）、式（7）、式（8）：

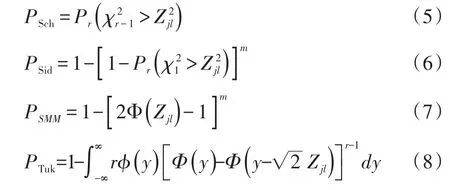
2 未分层生存函数趋势检验

2.1 未分层生存函数趋势检验的检验假设

Klein和Moeschberger于1997年提出了生存资料的趋势检验方法，该法有如下两个备择检验假设，根据实际资料，选择其中之一。

H2：S1(t)≥S2(t)≥ …≥SK(t)，t≤τ，至少有一个不等式成立；

或H2：S1(t)≤S2(t)≤ …≤SK(t)，t≤τ，至少有一个不等式成立。

2.2 未分层生存函数趋势检验的假设检验的计算公式

让a1＜a2＜…＜aK代表与K个样本有关联的一组得分，则在H0成立的条件下，对应的检验统计量如下：

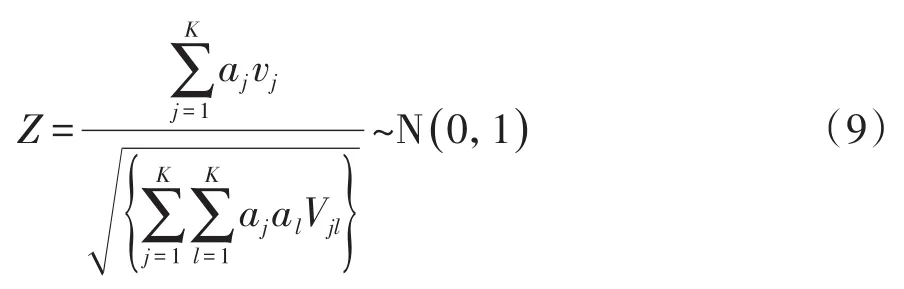
3 协变量的秩检验

3.1 协变量及其处理方法简介

在生存资料的差异性分析中，通常涉及定性的影响因素（包括试验因素和/或分层因素，后者在本质上属于“重要非试验因素”）和定量的结果变量（即生存时间）。然而，在很多生存资料中，还涉及定量的和二值的影响因素或自变量，它们常被称为“协变量”。考察协变量对生存函数的影响，最常见的做法是把所有需要考察的“影响因素（包括试验因素、重要非试验因素和协变量）”都当作自变量，把生存时间或生存时间的函数作为因变量，进行生存资料的多重回归分析。当因变量为生存时间时，需要拟合生存资料的参数回归模型；当因变量为生存时间的函数（例如危险率函数）时，需要拟合COX比例风险或非比例风险回归模型。在SAS/STAT的“LIFETEST”过程中，还介绍了另一种处理协变量的方法，即采用“秩检验”来研究协变量对生存函数的影响是否有统计学意义。

3.2 单协变量秩检验统计量

单协变量时，检验其对生存函数的影响是否有统计学意义，所对应的秩检验统计量见式（10）：

在式（10）中，χ2服从自由度为1的χ2分布；v为基于协变量计算得到的“一般秩统计量”；V是v的方差。

3.3 多协变量秩检验统计量

多协变量时，检验它们对生存函数的影响是否有统计学意义，所对应的秩检验统计量见式（11）：

在式（11）中，χ2服从自由度为df的χ2分布；自由度df为“当前”所考查的协变量的个数；v为基于协变量向量计算得到的“一般秩统计量”；V是基于v的“方差与协方差矩阵”，此矩阵主对角线上的元素就是与各协变量对应的“一般秩统计量”的方差。

值得注意的是：式（11）不是一个恒定的公式，其中所包含的协变量的个数由1个逐渐递增到全部需要考查的协变量（不妨设共有L个协变量），每次都对应着一个χ2检验结果（包括一个χ2值和一个P值）。首先基于单协变量检验法选取对生存函数影响最大的单个协变量，第二次选取能使χ2值获得最大增量的协变量，依次类推，逐一增加协变量，直至需要考查的协变量全部进入式（11）。例如：在本文例1中考虑了5个协变量，经过5次搜索并代入式（11）计算，由输出结果（参见本文例1中输出结果最后部分“对数秩检验的卡方向前逐步序列”）第二列可以看出，自由度数目在逐次增加1；由第三列可以看出，χ2值逐渐增大；由第5列可看出，χ2值的增量逐渐减小，因为后面选取的协变量比之前选取的协变量对生存函数的影响小。由于式（10）是式（11）的特例，故下面仅针对式（11），介绍其有关细节。

3.4 式（11）中的有关细节

3.4.1 一般秩统计量的计算公式

在式（11）中，v为基于协变量计算得到的“一般秩统计量”，当只考查一个协变量时，其计算结果就是一个具体的“秩和”；当考查的协变量个数大于等于2时，其计算结果就是一个“向量”，其各分量是与各协变量对应的“秩和”。v的计算方法如下：

在式（12）中，n为总样本含量；Cα，δα为秩得分（即把生存时间数据按由小到大排序并赋予秩次或称为打分），δα为指示变量，δα=1代表观测到的为“事件（即准确的生存时间）”，δα=0代表观测到的为“删失（即截尾的生存时间）”；Zα是与第α个观测或个体对应的全部协变量取值组成的向量。

在SAS/STAT的“LIFETEST”过程中，有两种定义秩得分Cα，δα的方法，分别为“对数秩秩得分”和“威尔科克森秩得分”。

3.4.2 对数秩秩得分的计算公式

对数秩秩得分的定义如下：

在式（13）中，j为排序后的事件时间的编号，其对应的时间记为t（j）；ta代表所有的排序时间（包括事件时间和删失时间）；nj为恰好在t（j）之前危险集中个体的数目。

3.4.3 威尔科克森秩得分的计算公式

威尔科克森秩得分的定义如下：

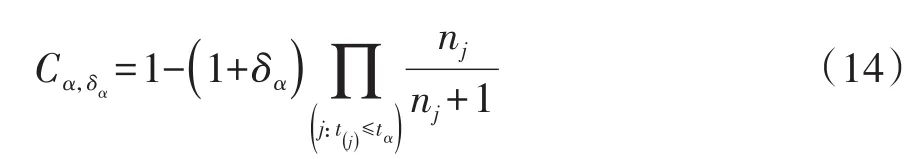
式（14）中各变量的含义与式（13）相同，此处不再赘述。

3.4.4 用于估计对数秩统计量的协方差矩阵的计算公式

用于估计对数秩统计量的协方差矩阵的计算方法见式（15）：

在式（15）中，Vi是在时刻t（i）风险集的校正平方和以及交叉乘积和矩阵，其计算方法如下：

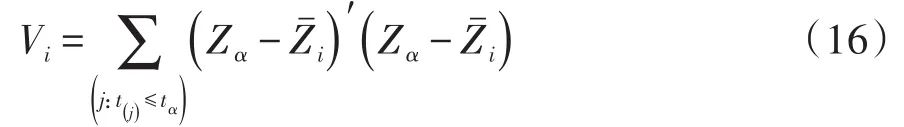
3.4.5 用于估计威尔科克森统计量的协方差矩阵的计算公式

用于估计威尔科克森统计量的协方差矩阵的计算公式见式（18）：

式（18）中A和B的计算公式分别见式（19）、式（20）：

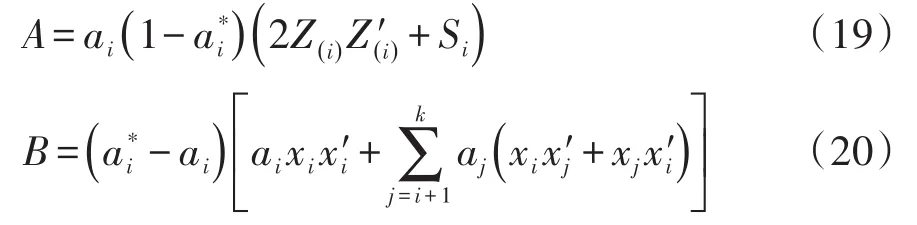
在式（19）、式（20）中，有关变量的含义如下：

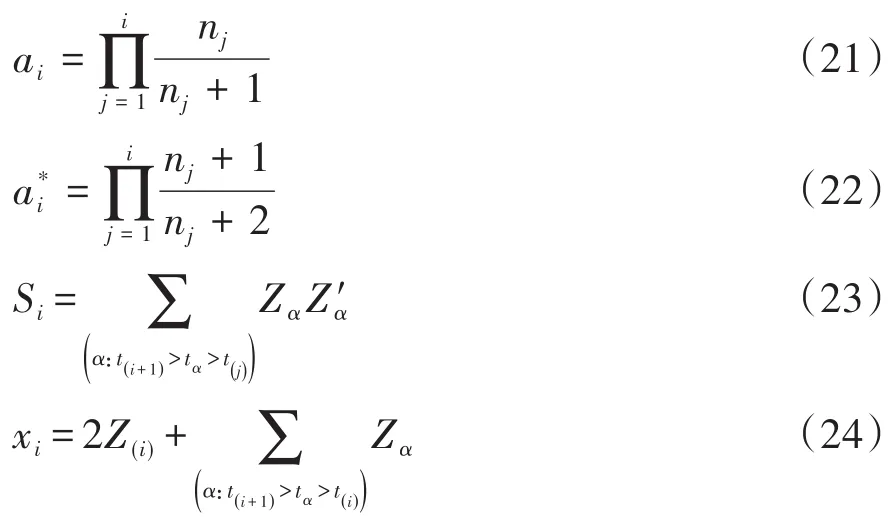
【说明】为便于理解，对以上公式的内容扼要梳理：式（11）中的“v”由式（12）给出；式（11）中的“V”由式（15）或式（18）给出；式（10）的更一般表达见式（25）：

在式（25）中，vi是式（12）中第i个分量；Vii是式（15）或式（18）中矩阵V的主对角线上第i个元素。

4 实例及SAS实现

4.1 问题与数据

【例1】沿用本期科研方法专题《如何正确运用χ2检验——生存资料的似然比检验与六种非参数检验与SAS实现》一文中“例2的问题与数据”，试完成下列三项任务：任务一：对四种癌细胞类型的生存曲线进行两种情形下的多重比较；任务二：对四种癌细胞类型的生存曲线进行趋势检验；任务三：对四种癌细胞类型的生存曲线进行比较，并检验5个协变量对生存曲线的影响。

4.2 SAS实现

【分析与解答】设所需要的SAS程序如下：

任务一的主要输出结果：两两比较。

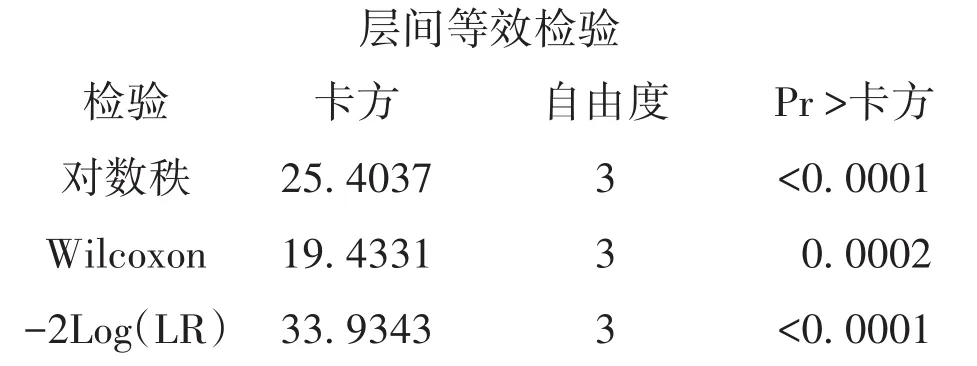
以上输出结果表明：四种癌细胞类型的患者生存曲线之间差别有统计学意义。

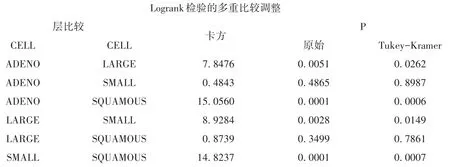
以上是在对数秩检验后再进行两两比较的计算结果，具体地说，是关于“四种癌细胞类型的患者生存曲线两两之间的差别”的两种假设检验结果，一种是未校正的计算结果，另一种是基于“Tukey-Kramer法”校正的计算结果。其中，腺癌与大细胞癌、腺癌与鳞癌、大细胞癌与小细胞癌、小细胞癌与鳞癌患者生存曲线之间差异有统计学意义。

为节省篇幅，在采用Wilcoxon检验后再进行两两比较的计算结果从略。

任务一的主要输出结果：与对照组比较。

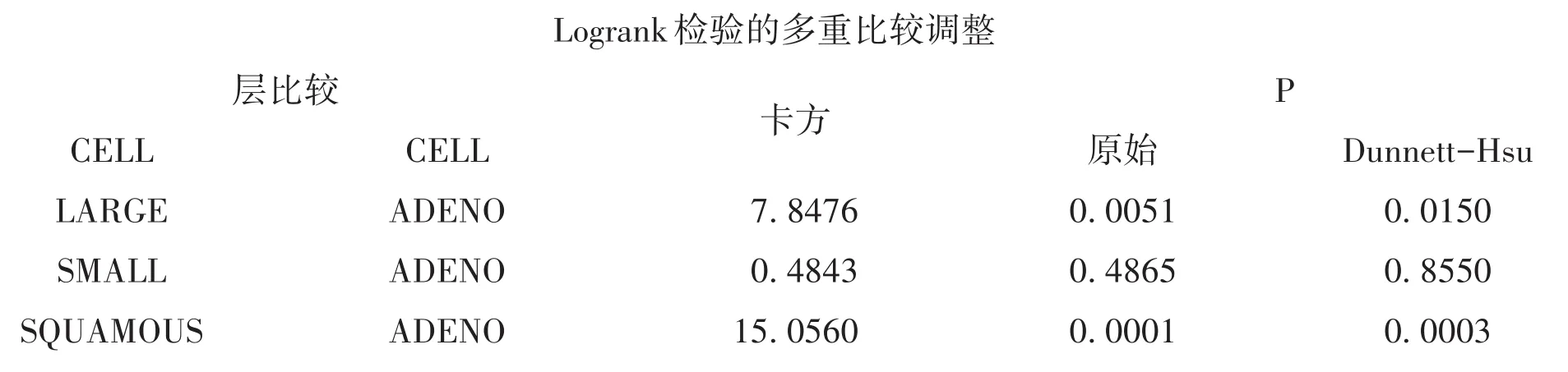
以上是基于“对数秩检验的多重比较调整”计算所得的结果，此结果表明：以腺癌为对照组，大细胞癌和鳞癌与腺癌患者生存函数之间的差别有统计学意义。为节省篇幅，在采用Wilcoxon检验后再进行与对照组比较的计算结果从略。

四种癌细胞类型的患者生存时间的P25、P50、均值、P75的计算结果见表1。

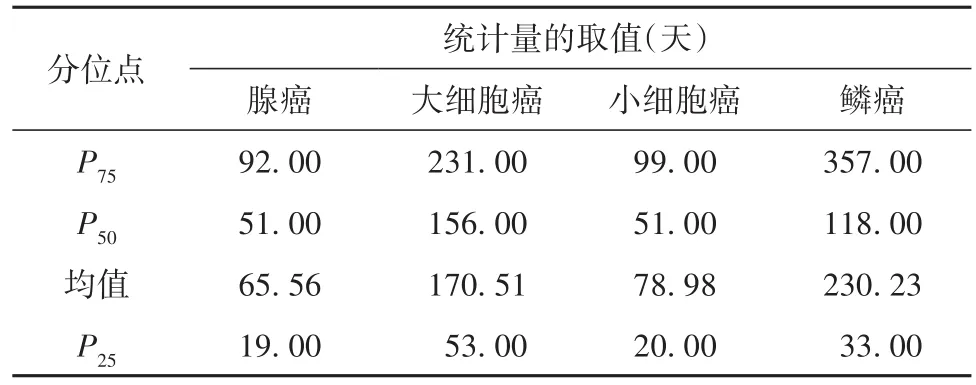
表1 四种癌细胞患者生存时间的4种分位数计算结果

任务二的主要输出结果。

以上输出的是趋势检验结果：第一行为基于“对数秩法”计算的结果，第二行为基于“威尔科克森法”计算的结果，倒数第三列为双侧检验的结果，倒数第二列为左单侧检验的结果，最后一列为右单侧检验结果。

“威尔科克森法”计算结果表明：四种癌细胞类型的患者生存曲线之间不存在递增或递减的变化趋势；而“对数秩法”计算结果表明：四种癌细胞类型的患者生存曲线之间存在递增或递减的变化趋势（以双侧检验为依据）。

任务三的主要输出结果。

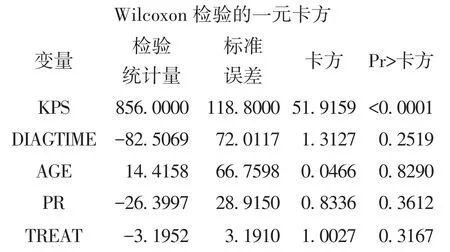
以上是基于“威尔科克森法”进行单协变量分析所得的计算结果，此结果表明：仅KPS一个协变量对生存函数的影响有统计学意义。

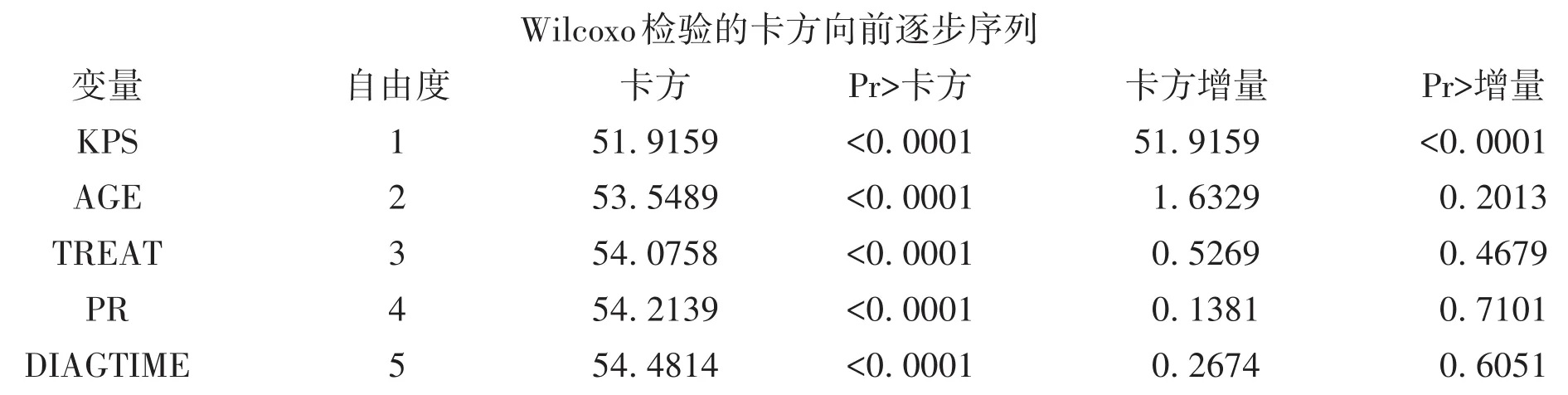
以上是基于“威尔科克森法”进行累加协变量分析所得的计算结果，此结果表明：仅KPS一个协变量对生存函数的影响有统计学意义。

为节省篇幅，采用对数秩检验输出的结果与前面类似的两部分计算结果从略。

基于“对数秩法”进行单协变量分析所得的计算结果表明：仅KPS一个协变量对生存函数的影响有统计学意义。

基于“对数秩法”进行累加协变量分析所得的计算结果表明：仅KPS一个协变量对生存函数的影响有统计学意义。

【统计结论和专业结论】由多重比较的情形一，即两两比较的结果可知：腺癌与大细胞癌、腺癌与鳞癌、大细胞癌与小细胞癌、小细胞癌与鳞癌患者生存函数之间差异有统计学意义；结合四种癌细胞类型患者生存时间的中位生存期（见表1）可知，大细胞癌患者的中位生存期最长，鳞癌患者的中位生存期次之，腺癌与小细胞癌患者的中位生存期相等且最短。

由多重比较的情形二，即与对照组比较的结果可知：以腺癌为对照组，大细胞癌和鳞癌与腺癌患者生存函数之间差异有统计学意义；小细胞癌与腺癌患者生存函数之间差异无统计学意义。专业结论与“两两比较的结论”相同。

由趋势检验的结果可知：基于“对数秩法”和“威尔科克森法”计算的结果之间存在矛盾，前者认为：四种癌细胞类型的患者生存曲线之间存在递增或递减的变化趋势（以双侧检验为依据）；而后者认为：四种癌细胞类型的患者生存曲线之间不存在递增或递减的变化趋势（以双侧检验为依据）。

由协变量检验的结果可知：仅KPS一个协变量对生存函数的影响有统计学意义。在其他影响因素取特定值的条件下，该变量的取值越大，患者的生存时间越长。

5 讨论与小结

5.1 讨论

在对多因素生存资料进行假设检验时，有一个值得注意的问题：试验因素各水平下的生存曲线之间的差别，不仅取决于计算方法（总共有7种，包括似然比检验方法和六种非参数检验方法［1］），还取决于是否考虑分层因素，但与是否考虑协变量检验无关。严格地说，既然是多因素生存资料，在进行生存分析时，就应当同时考虑全部试验因素、重要非试验因素（即协变量）及其交互作用项对生存函数的影响，而不适合进行多次单因素分析。一般来说，采取多重回归分析方法（包括Cox比例风险与非比例风险回归模型分析法、参数模型回归分析法［1-8］）处理多因素生存资料，能更真实地揭示多因素对生存函数的影响规律。

5.2 小结

本文介绍了生存资料的三种特殊检验方法，即多重比较、趋势检验和协变量检验。其中，多重比较包括两两比较和与一个对照组比较的两种情形，在两两比较中，又有约10种具体的校正方法；在趋势检验中，包括“对数秩检验法”和“威尔科克森检验法”两种，它们的计算结果可能接近，也可能相差甚远；在协变量检验中，可以对单个协变量进行检验，也可以对逐次累加的多个协变量进行检验。