如何正确运用χ2检验<br/>——生存资料的似然比检验和六种非参数检验与SAS实现

如何正确运用χ2检验
——生存资料的似然比检验和六种非参数检验与SAS实现

2021-11-04胡纯严胡良平

四川精神卫生 2021年5期

胡纯严，胡良平，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在临床研究中，生存资料出现的频率很高［1-7］。生存时间t是生存资料中的结果变量，它具有两个明显的特点：①生存时间一般不服从正态分布；②生存资料中常包含删失数据或称为不完全数据。因此，对生存资料进行统计分析的方法有别于常规的统计分析方法。本文将结合实例，介绍单因素和多因素生存资料的差异性检验方法，包括似然比检验方法和六种非参数检验方法。

1 生存函数假设检验的基础

1.1 生存函数的定义

生存分布函数（SDF）也叫生存函数，常用符号S（t）表示，它描述感兴趣的总体（群体）的寿命时间［8］。在t时刻SDF的估计值是来自总体的试验单元（或受试对象）的寿命时间超过t的概率，即有下式：

式（1）中的S（t）为生存函数，T是随机选择的一个试验单元（或受试对象）的寿命时间。

1.2 基本变量的定义

让t1＜t2＜…＜tD代表不同的事件时间。对每一个i（i=1，2，…，D），让Yi代表ti时刻之前的生存单元数目（即风险集的大小），让di代表ti时刻的失效或死亡的数目。

1.3 生存函数的估计

1.3.1 生存函数的Breslow估计

注意：Breslow估计是累计危险函数的负Nelson-Aalen估计的指数。

1.3.2 生存函数的Fleming-Harrington估计

如果频数值不是整数，就不能计算Fleming-Harrington估计。

1.3.3 生存函数的Kaplan-Meier估计

在ti时刻的生存函数的Kaplan-Meier估计（乘积-极限）是累计乘积：

注意：式（2）、式（3）、式（4）定义的生存函数估计量都是右连续的，也就是说，在ti时刻发生的事件应该被包含在S（ti）的估计之中。

1.4 生存函数的标准误

由Kalbfleisch和Prentice于1980年提出生存函数标准误的格林伍德（Greenwood）估计公式如下：

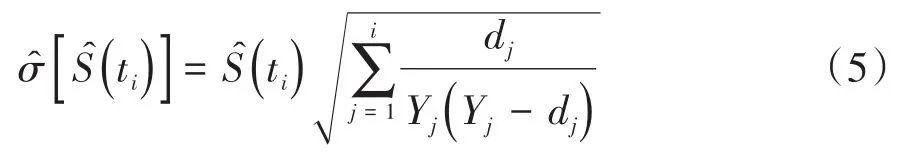
1.5 两个或多个生存函数相等的检验假设

让K代表组数，Sk（t）代表第k组中的生存函数（k=1，2，…，K）。于是，被检验的无效假设和备择假设分别如下。

H0：S1(t)=S2(t)=…=SK(t)，对于所有的t≤τ都成立；

H1：至少有一个Sk(t)是不同的，对于某些t≤τ成立。

2 未分层生存函数相等的假设检验计算公式

2.1 似然比检验

Lawless于1982年基于各组生存资料服从指数分布的假定，推导出检验前述“检验假设”的似然比统计量［8］，见下式：

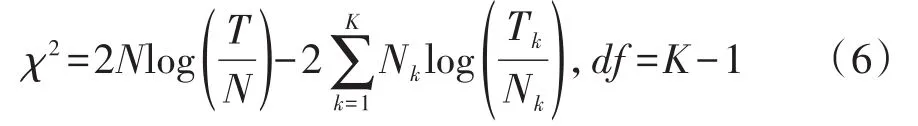
在式（6）中，χ2是服从自由度为df=K－1的χ2分布的随机变量（此处也叫做“检验统计量”）；Nk为第k组中事件总数（在生存分析中为“死亡”人数）；；Tk为第k组中参与检验的全部生存时间之和；。

2.2 六种非参数检验

2.2.1 六种非参数检验的名称

在SAS/STAT的“LIFETEST”过程中，有六种用于比较两组或多组生存资料的生存函数是否相等的假设检验方法［8］，分别是对数秩（Log-rank）检验、威尔科克森（Wilcoxcon）检验、Tarone-Ware检验、Peto-Peto检验、修正的Peto-Peto检验和Harrington-Fleming（p，q）检验。

2.2.2 基本变量的定义

让(Ti，δi，Xi)，i=1，2，…，n，代表具有右删失生存资料的一个独立样本，Ti是一个可能的右删失的时间；δi是一个删失的指示变量（δi=0代表Ti是删失时间，δi=1代表Ti不是删失时间，即事件发生的时间）；Xi=1，2，…，K代表K个不同的组；让t1＜t2＜…＜tD代表样本中不同的事件时间。在时刻Tj，让W（tj）代表一个正权重函数（简称“权函数”），让Yjk和djk分别代表第k组中的风险集的大小和事件的数目，其中，。再分别让。

2.2.3 六种非参数检验对应的权函数

六种非参数检验的检验统计量无论是在本质上还是在表达形式上都是一样的，所不同的仅仅是权函数，见表1。

表1 生存资料六种非参数检验对应的权函数

2.2.4 六种非参数检验的共同检验统计量

六种非参数检验的共同检验统计量见式（7）：

在式（7）中，χ2服从自由度为df=矩阵V的秩的χ2分布；v'是v的转置向量；V-是矩阵V的广义逆矩阵。式（7）中等号右边各变量的具体含义如下：

在式（8）中，各分量的计算公式见式（10）：

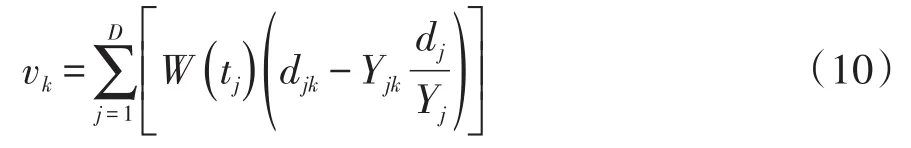
在式（10）中，W（tj）为权函数，其定义参见前面的表1。在式（9）中，V是由vk的方差和vk与vh之间的协方差组成的矩阵，其各元素的定义如下：

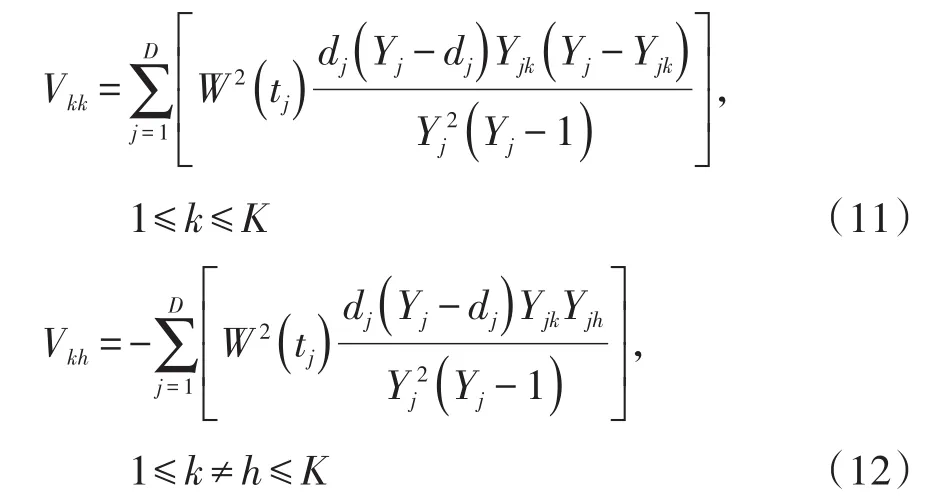
2.3 校正的对数秩检验

校正的对数秩检验的检验统计量见式（13）：

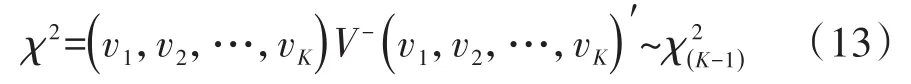
在式（13）中，χ2服从自由度为K-1的χ2分布，它是对加权的K个样本的生存函数进行检验的检验统计量。式（13）中等号右边各变量的含义和定义如下：

让 (Ti，δi，Xi，wi)，i=1，2，…，n，代表具有右删失的生存资料的一个独立样本，Ti是一个可能的右删失的时间；δi是一个删失的指示变量（δi=0代表Ti是删失时间，δi=1代表Ti不是删失时间，即事件发生的时间）；Xi=1，2，…，K代表K个不同的组；wi是LIFETEST过程的“WEIGHT”语句中指定变量在各观测上的取值；让t1＜t2＜…＜tD代表样本中不同的事件时间，在时刻Tj（j=1，2，…，D），并且，对于每一个1≤k≤K，则有下式：

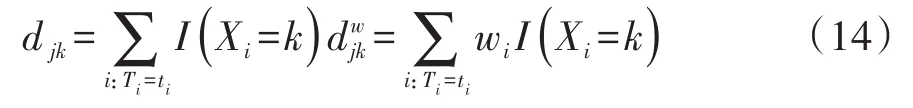
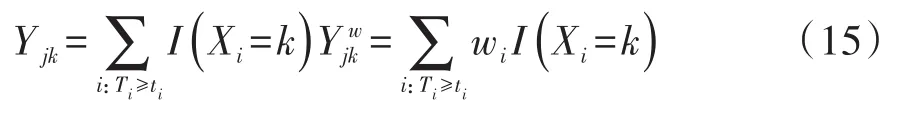
在时刻tj合并的样本中，让和分别代表风险集的大小和事件的数目，让分别代表风险集中权重的数目和事件的权重数目。于是，在式（13）中，向量v中的各分量和矩阵V=（Vkh）中的各元素（即方差与协方差）分别见式（16）、式（17）、式（18）：

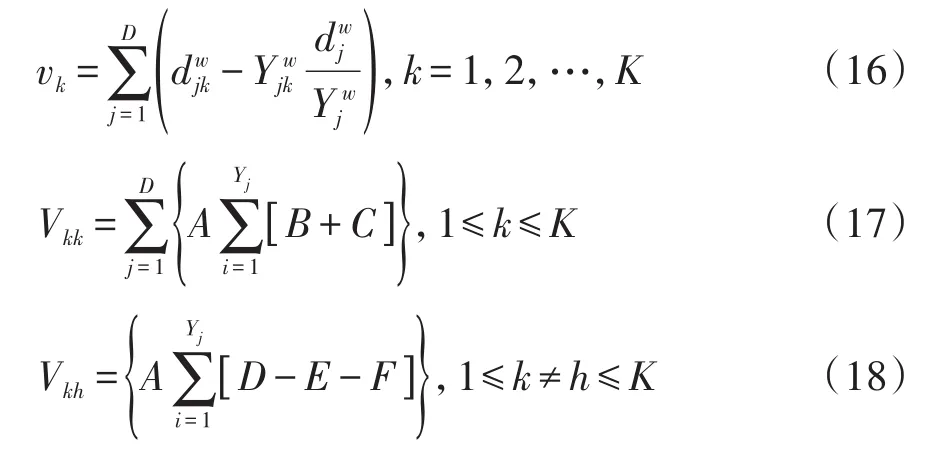
在式（17）中，A、B和C的内容分别如下：

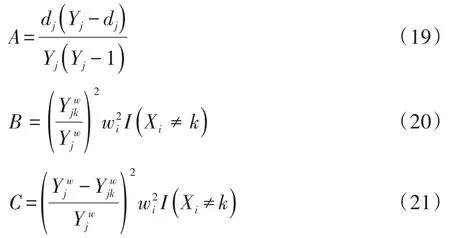
在式（18）中，A的内容与式（19）相同；D、E和F的内容分别如下：

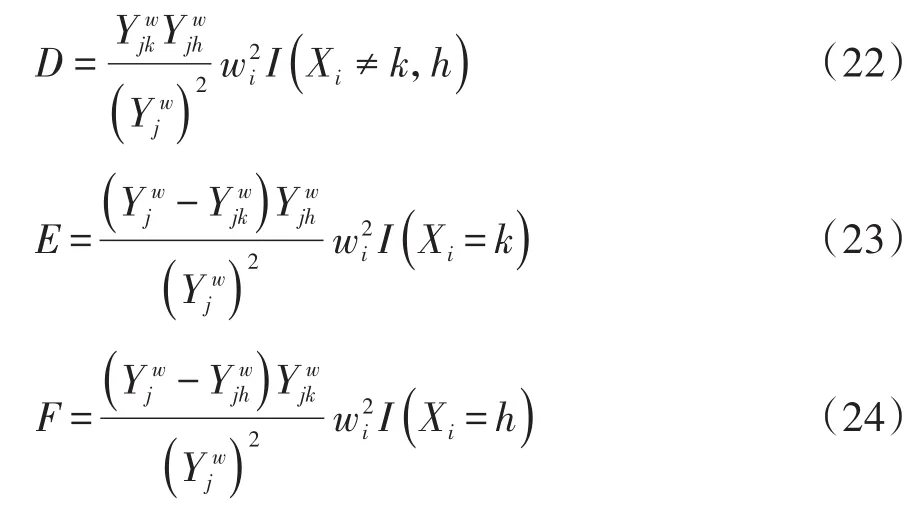
3 分层生存函数相等的假设检验的计算公式

3.1 何为分层生存函数相等的假设检验问题

假定在生存资料中，有一个具有M水平的分层因素，在其各水平下均有一个具有K水平的重要试验因素。于是，就需要考虑将M层生存函数按那个重要试验因素分别合并起来，再进行合并后的K个生存函数是否相等的检验，这就是分层生存函数相等的假设检验问题。

3.2 分层生存函数相等的检验统计量

进行分层生存函数相等的假设检验，Klein和Moeschberger于1997年提出了如下方法：设分层因素有M个水平、重要试验因素有K个水平、第s（s=1，2，…，M）层中的检验统计量为vs，于是，对合并后的生存函数进行假设检验的检验统计量见下式：

式（25）中的χ2服从自由度为df=各层中协方差矩阵V的秩的χ2分布；v'是v的转置向量；V-是协方差矩阵V的广义逆矩阵。式（25）中等号右边各变量的具体含义如下：

4 实例及SAS实现

4.1 问题与数据

【例1】（未分层生存资料）将26例白血病患者分为两组，分别采用化疗、化疗联合中药两种方法，治疗后患者存活数（月）如下，其中带“+”号的为终检值。试估计两组患者的生存率，并比较两种方法治疗白血病患者的生存率差异是否有统计学意义［9］。化疗组（A）：2+，13，7+，11+，6，1，11，3，17，7；化疗联合中药组（B）：10，2+，12+，13，18，6+，19+，26，9+，8+，6+，43+，9，4，31，24。

【例2】（分层生存资料）某医院肿瘤科提供的一份关于肺癌患者的失效时间资料［8］，因变量为患者治疗后的生存时间t（d），当t为删失数据时，在前面加一个负号表示；考察的协变量（即危险因素或预后因素）如下：①癌细胞的类型，它有4个水平，即腺癌细胞、鳞癌细胞、小细胞肺癌和大细胞肺癌；②治疗类型，它有2个水平，即标准的方法和试验的方法；③疗前处理，它有2个水平，即采取了疗前处理和未采取疗前处理；④患者年龄（岁）；⑤从诊断到治疗的等待时间；⑥患者的行动状态用Karnofsky率来度量，其取值用KPS表示，0≤KPS≤10表明患者完全靠医院护理，40≤KPS≤60表明患者的行动部分受到限制，70≤KPS≤90表明患者的行动可以自理。前3个变量被当作分类变量，后3个变量被当作连续性变量。资料的形式为：各组患者的治疗方法、癌细胞类型、同一组中的样本含量、生存时间、KPS值、等待时间、年龄、与疗前处理对应的指示变量PR值（注：PR=0等价于令PRIOR='YES'，即表示采取了疗前处理；PR=10等价于令PRIOR='NO'，即表示未采取疗前处理）。（说明：因数据量很大，各变量取值从略，可查阅参考文献［8］）

试按下面两个要求分析此生存资料：其一，仅按“治疗方法”一个因素分层，比较4种癌细胞类型患者的生存曲线差异是否有统计学意义；其二，同时按“治疗方法”和“有无疗前处理”两个因素分层，比较4种癌细胞类型患者的生存曲线差异是否有统计学意义。

4.2 基于SAS软件分析例1资料

【分析与解答】设所需要的SAS程序如下：

【程序说明】在“strata”语句中，选项“test=all”代表选择六种非参数假设检验方法，其中，fleming（ρ1，ρ2）自动设置为：fleming（1），即 ρ1=1、ρ2=0；当特别指定ρ1、ρ2为非负数且不为0时，对应的计算结果会随着这两个参数的具体取值而发生改变，例如：给定fleming（1，4）与fleming（2，5）时，对应的χ2值和P值是不同的；如果要求输出“似然比检验”结果，必须加上选项“LR”。

【SAS输出结果及解释】

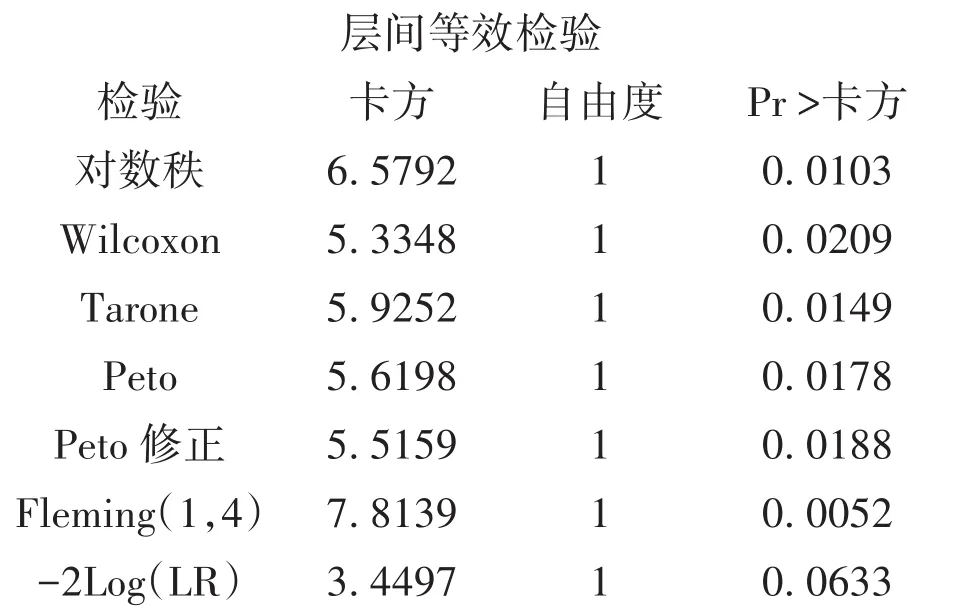
以上输出结果中，前6行是六种非参数检验结果，最后一行是似然比检验结果。前6行检验结果都得到“P＜0.05”的结果；而最后一行的结果为“P＞0.05”。当生存资料服从“指数分布”时，应选取“似然比检验”结果；当生存资料服从“威布尔分布”时，应选取“对数秩检验”结果；否则，可以考虑选取其他非参数检验结果。通过查看图1和图2，可大致判断出本例生存时间资料服从何种分布。

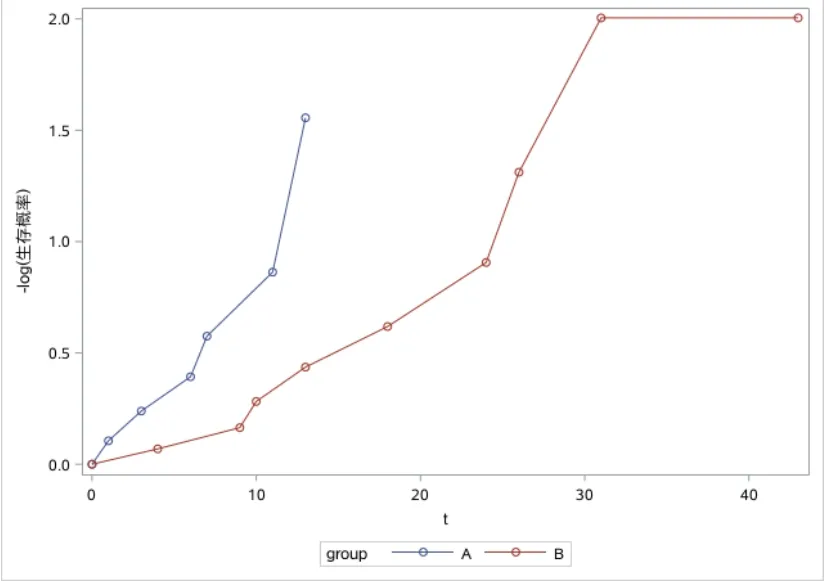
图1 用于判断生存资料是否服从指数分布的图形

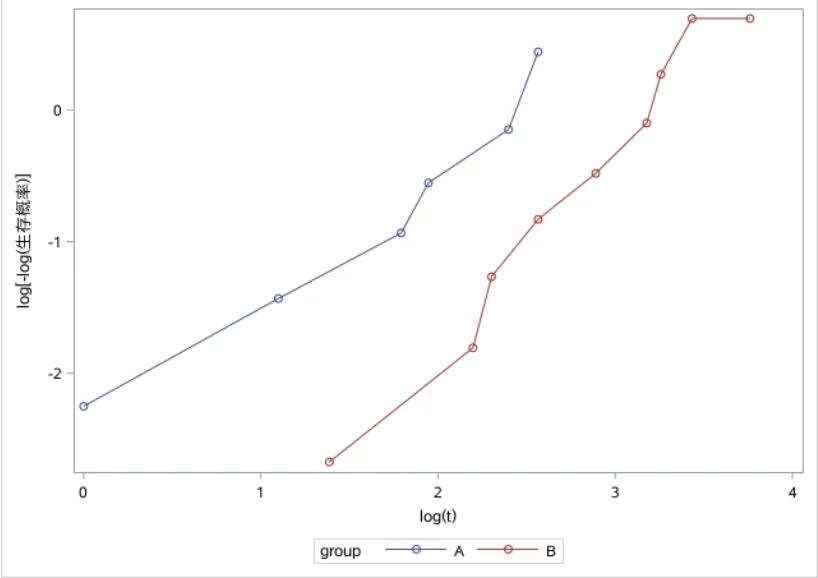
图2 用于判断生存资料是否服从威布尔分布的图形

在图1中，两条折线都不呈直线，说明本例两组生存资料都不服从指数分布；而在图2中，两条折线都近似呈直线，说明本例两组生存资料都近似服从威布尔分布。由此可知，本例的假设检验结果以选择“对数秩检验”结果为宜。为了便于直观判断哪一种治疗方法所对应的患者生存时间更长，需要呈现出他们的生存率曲线，见图3。

在图3中，左边的生存曲线为“A组（化疗组）”；右边的生存曲线为“B组（化疗联合中药组）”。

【统计结论与专业结论】因χ2=6.5792，df=1，P=0.0103＜0.05，说明两条生存曲线之间的差异有统计学意义；由于B组（化疗联合中药组）的生存曲线位于A组（化疗组）生存曲线的右边（见图3），说明“化疗联合中药”治疗的效果优于“单纯化疗”的效果。

4.3 基于SAS软件分析例2资料

【分析与解答】设所需要的SAS程序如下：

因篇幅所限，第1个过程步的主要输出结果此处从略，仅给出概括性结论。第一层：标准治疗组。标准治疗的4种癌细胞类型的生存曲线之间的差别所对应的P值均小于0.05，大细胞肺癌患者的生存曲线最长。第二层：试验治疗组。试验治疗的4种癌细胞类型的生存曲线之间的差别所对应的P值均小于0.05，肺鳞癌细胞患者的生存曲线最长。

因篇幅所限，第2个过程步的主要输出结果此处从略，仅给出概括性结论。第一层：标准治疗且未接受预处理，结果显示，三种方法对应的结果为P＞0.05，有4种方法对应的P＜0.05。第二层：标准治疗但接受预处理，结果显示，七种方法对应的结果均为P＞0.05。第三层：试验治疗且未接受预处理，结果显示，七种方法对应的结果均为P＜0.05。第四层：试验治疗但接受预处理，结果显示，前六种方法对应的结果均为P＞0.05，而最后的似然比检验结果为P＜0.05。

【统计结论与专业结论】本例资料按“治疗方法”与“是否接受预处理”所形成的四层来分别比较4种癌细胞的患者生存曲线，因分析结果不尽相同，故统计结论与专业结论都需要在各层的条件下进行具体描述，因篇幅所限，此处从略。

5 讨论与小结

5.1 讨论

在SAS/STAT的LIFETEST过程中，介绍了比较两组或多组生存资料的差异性检验方法，包括似然比检验和六种非参数检验。一般来说，在构建似然比检验统计量时，需要假定所研究的变量服从某种概率分布；而非参数检验，顾名思义，不假定所研究的资料服从何种概率分布。当各种非参数检验用于同一个资料产生出不同的检验结果时，如何选取最终的结果就成了一个棘手的问题。通常情况下，可以选择P值最小的非参数检验法给出的计算结果。例如，在例1的计算结果中，对数秩检验给出的P=0.0103、χ2=6.5792，而fleming（1，4）的P=0.0052、χ2=7.8139；若进一步尝试，还可得到fleming（3，6）的P=0.0051、χ2=7.8382。在例2的分析中，因篇幅所限，未分析定量变量（即协变量KPS DIAGTIME AGE）对生存时间的影响。

有一个易于误解之处：在SAS输出差异性检验结果时，呈现的标题为“层间等效检验”，似乎表明：其下方给出的假设检验结果是针对“分层因素”各水平计算出来的。其实，标题中的“层间”是指“试验因素各水平间”。在例2中，试验因素是“4种癌细胞类型”，第一种情况下的分层因素为“治疗方法”，第二种情况下有两个分层因素，即“治疗方法”与“是否接受预处理”。