圆筒水下爆炸冲击响应
2021-11-04贺平,严勇
贺 平,严 勇
(1. 中国船舶重工集团有限公司第七一〇研究所,湖北 宜昌 443003;2. 重庆钢铁股份有限公司,重庆 401220)
0 引言
圆筒结构受均匀外压作用时,只有径向的压力作用,而在周向不产生弯矩,因此广泛应用于各种水下结构中,如大型航行体——潜艇、潜器,小型的各种拖体。
在水雷、反水雷、反潜这些水下攻防领域,水下结构在工作中极易受到爆炸物的冲击,爆炸冲击会直接造成结构损伤和断裂,或造成搭载仪器设备工作失效。因此,研究和掌握圆筒类结构在水下爆炸冲击作用下的响应,对于推动我国水下攻防领域的研究与发展具有重要的意义。
水下爆炸对目标物的毁伤分为近场接触爆炸与远场非接触爆炸。近场接触爆炸,主要是通过水下爆炸冲击波和气泡脉动耦合作用使目标物产生严重破坏,比如:河道开凿爆破、水下兵器攻击破坏等。而在远场非接触爆炸中,主要是水下爆炸产生的冲击波对远距离目标物进行毁伤,因此冲击波产生和传播过程一直是抗爆防护研究的重点。本文主要研究远场非接触爆炸。
1 水下爆炸理论
1.1 概述
水下爆炸冲击波理论属于爆炸力学范畴,炸药在水域介质中爆炸,短时间内在炸药本身体积内形成的高压爆炸产物,使其压力远远超过静水压力。爆炸一般分为2个阶段:冲击波阶段和气泡脉动阶段。在冲击波阶段,冲击波波头幅值迅速达到最大,紧接着进行近似指数规律衰减,衰减持续时间只有数毫秒[1];在气泡脉动阶段,爆炸产物在水中形成膨胀收缩气泡的脉动压力对水下结构产生的作用称之为冲荡或振荡效应[2]。
在多数情况下,冲击波的破坏作用起决定作用。冲击波初始压力相当大,但随着冲击波的传播,其波阵面压力和速度迅速减小。冲击波过后,还会产生气泡脉动的现象形成脉动压力。非接触爆炸中的中远场距离爆炸时,冲击波载荷持续数毫秒,间隔数十毫秒至百毫秒之后,气泡脉动载荷才开始施加于结构上[3]。
流体与结构的耦合问题是水下爆炸响应分析中的关键点和难点。自20世纪50年代以来,科学家们开展了多种方法来解决这个问题。目前,解决水下爆炸流固耦合问题的方法主要有3种:1)不考虑流固耦合的影响,这种方法比较粗略,不可避免地会产生一定的误差,精确性差;2)采用双重渐近的方法,如迟滞势方法、可压缩流场边界积分法或附加质量法等近似解处理方法,这些方法大多是在每一计算步内根据上一步的计算结果预测流场力计算结构响应,再用结构响应计算流场的实际载荷,计算量非常大;3)完全的流固耦合算法,将结构的网格和流体的网格直接耦合在一起,流场的压力载荷通过耦合算法自动作用到结构的有限元网格上,结构的变形又反过来影响流场的流动[4]。这种结构变形和流体载荷间的相互影响,就得到耦合的流体-结构响应,一些有限元软件MSC.DYTRAN和ABAQUS等都采用这种算法来计算流固耦合问题。
1.2 声固耦合理论
将流体介质视为声学介质,流固耦合算法就变成了声固耦合,压力平衡方程如下[5]:
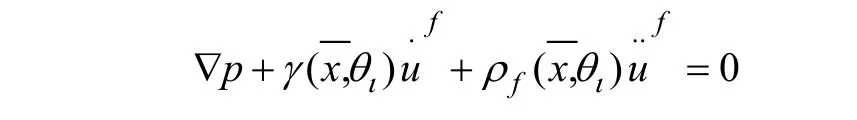
连续性方程:

式中:p为压力分布 ;ρf为流体密度 ;uf为流体质点的位移 ;Kf为流体的体积模量,当流体为水介质时,声音在水中传播速度c=1 465 m/s,此时Kf≈ 2.14×109Pa。
流体和结构的相互作用是该算法的关键,有限元分析中通过动量守衡将结构的位移场和流体的压力场耦合起来,在结构和流体的界面处采用不需要一一对应的网格,采用不同的网格密度和不同的单元模型。
爆源入射波加载,一个水下爆炸发生时会导致一个动力学特性气泡的产生,气泡的动力学特性将驱动声波在周围的流体中传播,这些声波撞击到结构表面就可能造成破坏损伤。给出炸药的位置、质量等特性,就能计算出施加到结构表面的随空间和时间变化的压力。
2 冲击波压力理论解析
Geers-Hunter基于声-结构耦合法基本假设,提出了冲击波-气泡统一计算模型,建立分段压力时程曲线,对水下爆炸压力全过程中的指数哀减阶段、倒数哀减阶段等分别给出了下述的解析公式[6-7]:
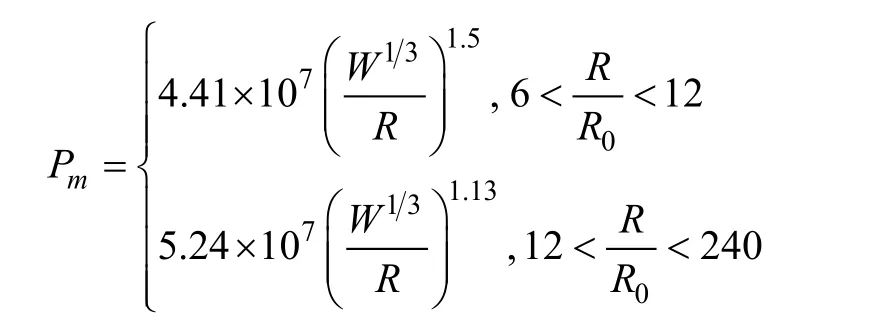
式中:Pm为冲击波压力峰值;W为TNT球状药包质量,kg;R为爆心到测点的距离,m;R0为药包的初始半径,m。

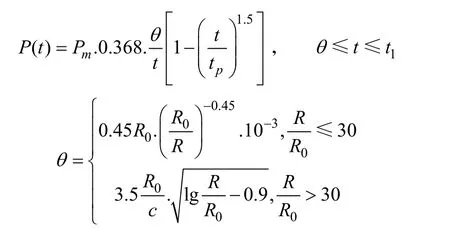
式中:e为冲击波时间哀减常数,s ;c为水中声速,m/s。
3 圆筒水下爆炸有限元分析
3.1 ABAQUS水下爆炸方法
ABAQUS在处理水下爆炸载荷时,采用声固耦合算法,该方法采用声学单元来描述流场。冲击波在声学单元中传播,采用理论公式来计算流场某一点处的压力或加速度时间历程曲线,然后该程序自动计算流场中的压力分布,在模拟远场水下爆炸时,不需要建立包含药包在内的所有流场。
ABAQUS在声固耦合算法中有2个最基本的假设:1)冲击波和气泡在水中产生的压力波近似用线性声学方程描述,于是冲击波-结构和气泡-结构的耦合理论统一使用声-结构耦合理论处理;2)结构可以发生非线性的大变形,但流体运动一直满足线性假定。第2条假设看似不合理,但考虑到结构的大变形尺度,对于流体来说仍是小变形,这条假设抓住了流体、结构变形的不同尺度特点,大大简化了计算。
ABAQUS中集成了水下爆炸冲击波-气泡统一计算模型,内含Undex模块,输入炸药相应参数后,ABAQUS会自动生成爆炸载荷的压力曲线[8-9]。
3.2 密封圆筒有限元模型
ABAQUS水下爆炸分析,结构周围的水域对计算结果非常重要。结构周围水域的影响主要分为以下3个方面:重力影响、阻尼影响和惯性(附加质量)影响。由于流场参与结构的总运动,使结构的等效质量发生变化,相当于有一部分流场与结构一起运动,该部分流场质量称为附加质量,它与结构体本身为同一量级。因此,该部分附加质量不能忽略。
密封圆筒计算模型,主尺度为ϕ0.2 m×1 m,壁厚 0.012 m,所处水深 30 m;爆源位于正下方20 m,TNT当量 100 kg,爆源点坐标(30.11,-1.387 6,0)。坐标系:水深方向为 x向,圆筒轴线方向为y向,圆筒径向水平方向为z向。
为保证计算精度的同时避免水域网格数量过多,外部流场半径选取为结构半径的6倍,水域包覆半径取0.6 m,外部流场采用声学单元模拟。有限元模型见图1。

图1 密封圆筒水下爆炸模型Fig.1 Underwater explosion model of sealed cylindrical shell
为便于仿真结果与经验公式理论值比较,在外流场靠近圆筒区域设置了冲击波压力观测点,观测点坐标为(0.046 4,-1.387 63,-0.143);同时,在圆筒靠近爆源区域设置了迎爆面、背爆面、侧面观测点,在远离爆源区域设置了远端观测点,分别监测其应力及加速度的时间历程变化情况。
3.3 计算结果
监测声源压力观测点声源压力的时间历程变化过程,得到冲击波压力时程曲线,按照第2章节中冲击波理论公式,得到了观测点冲击波压力理论值的时间历程变化曲线,计算结果见图2。
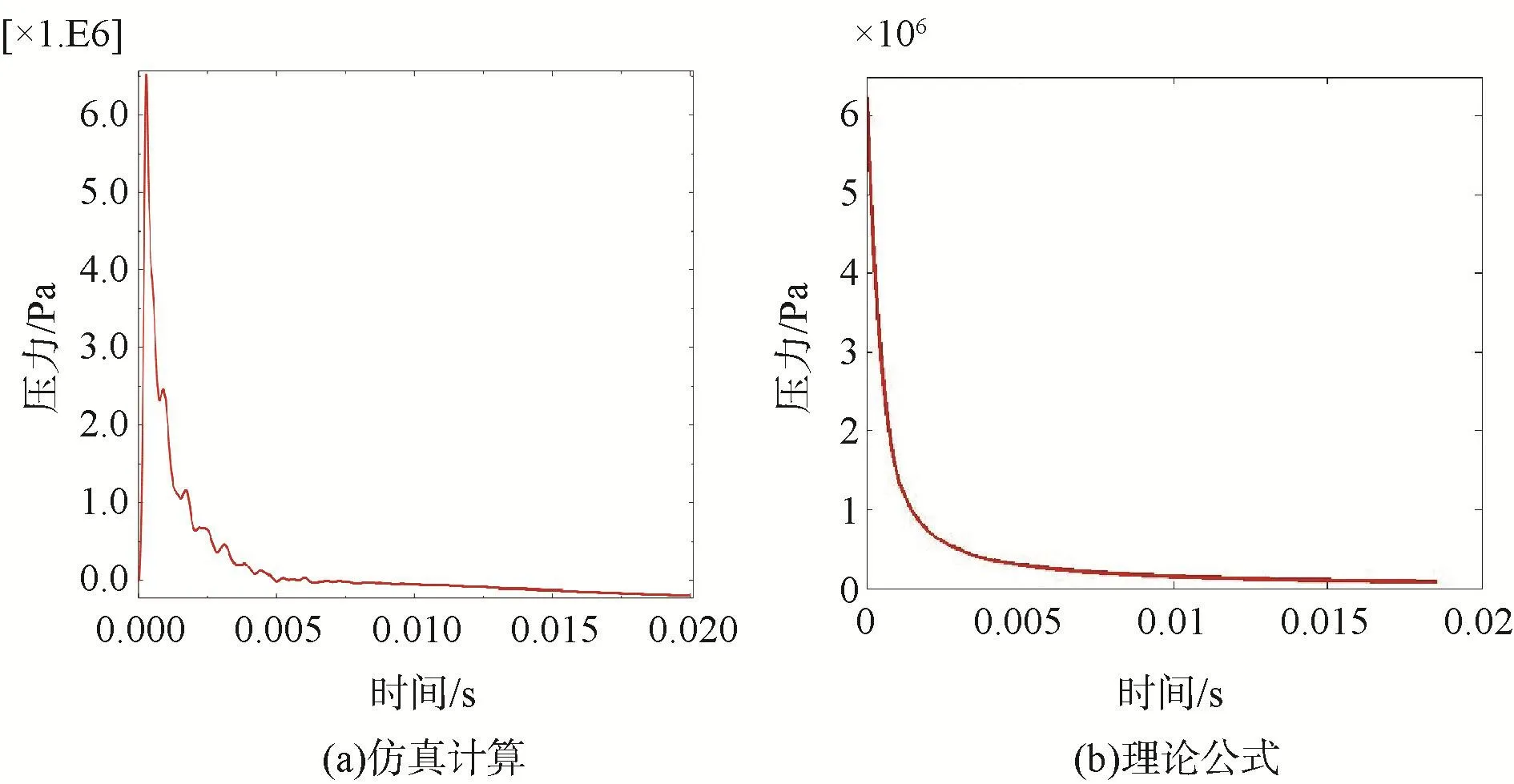
图2 观测点冲击波压力时程曲线Fig.2 Time-shock wave pressure curve at observation point
观测点冲击波压力时程曲线,仿真计算结果峰值为6.46 MPa,理论公式值约为6.26 MPa,仿真结果略大于理论公式结果,误差约3%。
水下爆炸冲击作用时间历程中,圆筒正对爆源迎爆面、背爆面、侧面以及远端观测点应力时程曲线见图3-6,加速度时程曲线见图7-10。
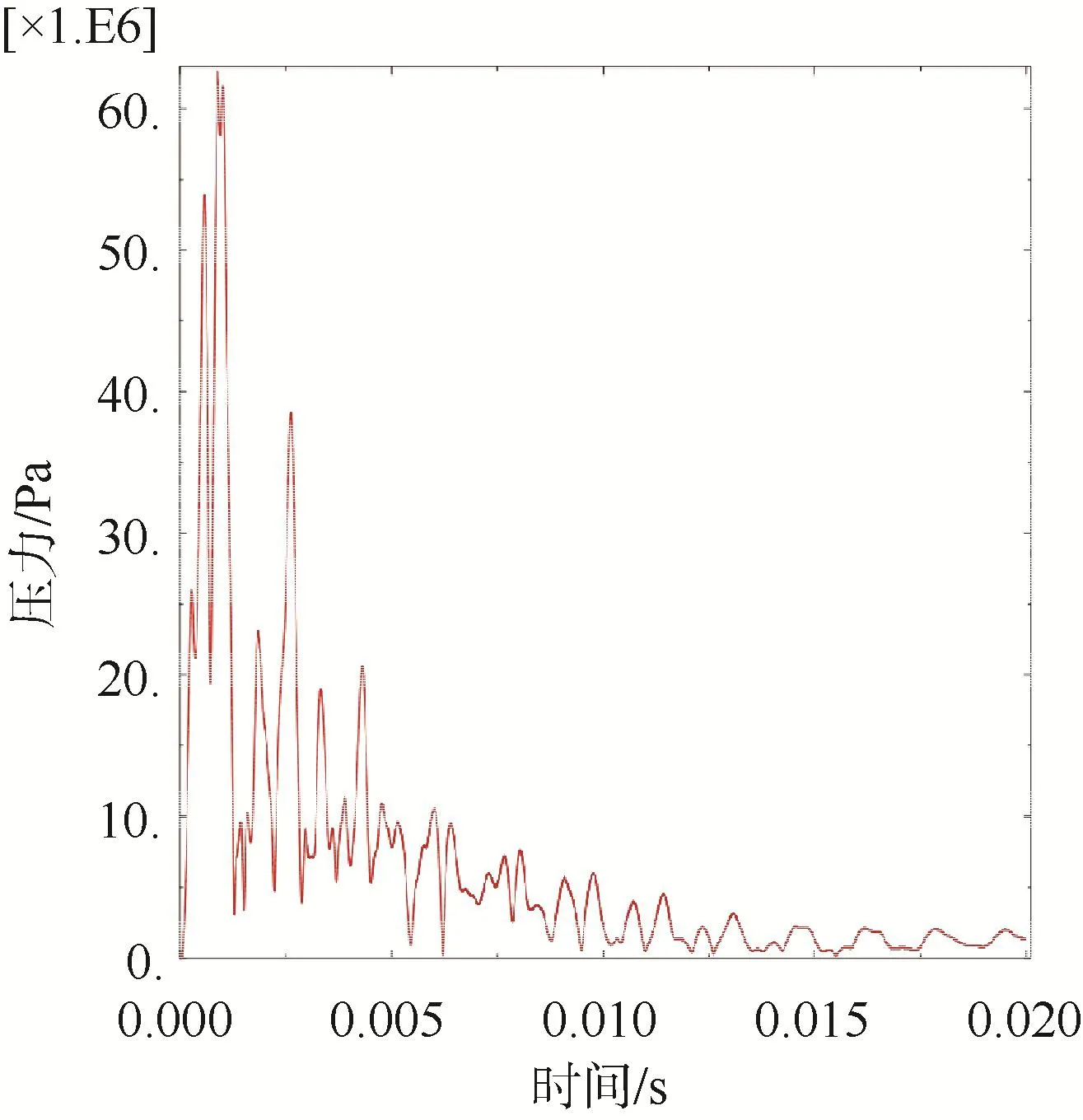
图3 迎爆面观测点应力Fig.3 Stress profile at observation point on leading surface

图4 侧爆面观测点应力Fig.4 Stress profile at observation point on side surface
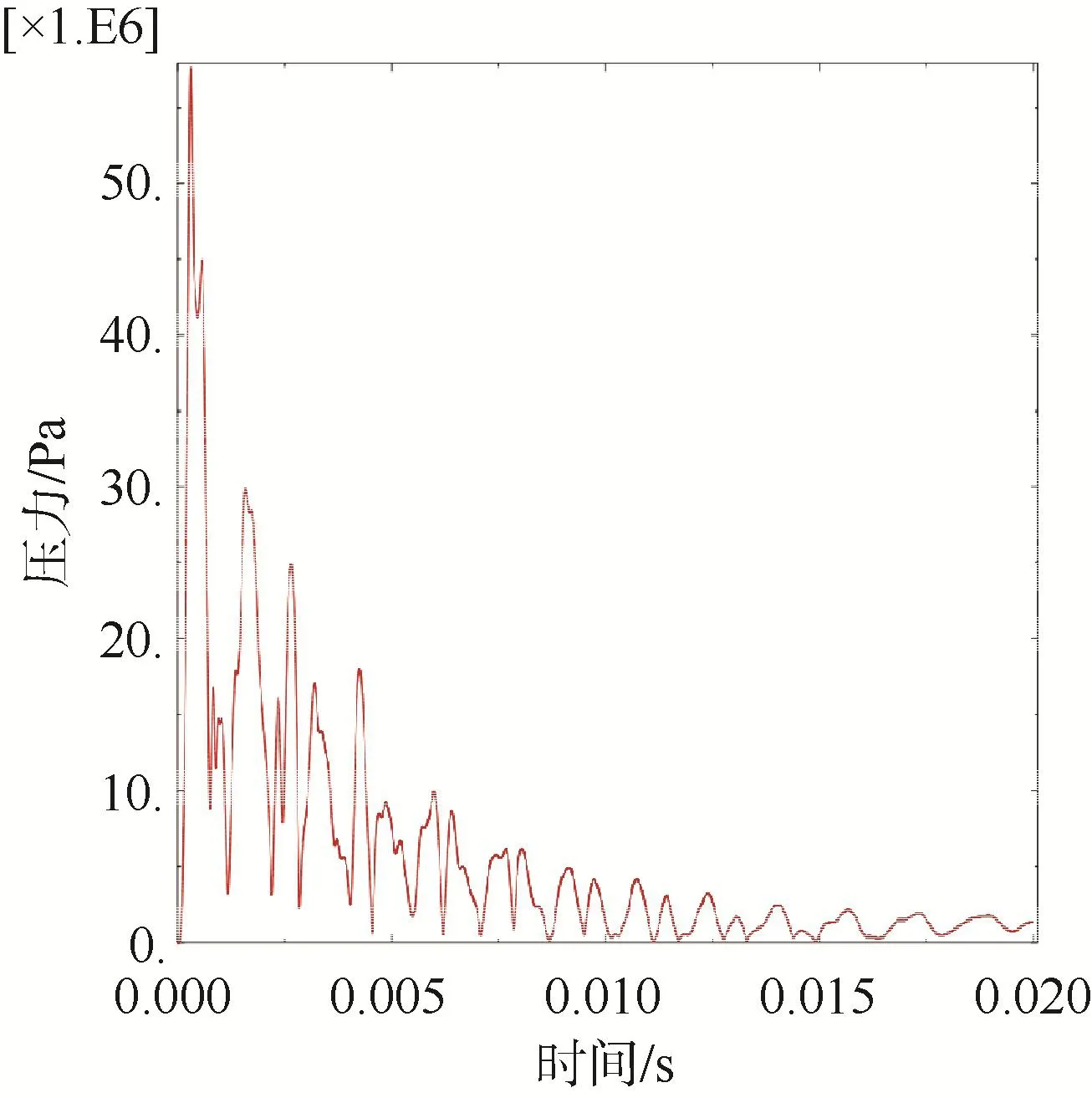
图5 背爆面观测点应力Fig.5 Stress profile at observation point on trailing surface
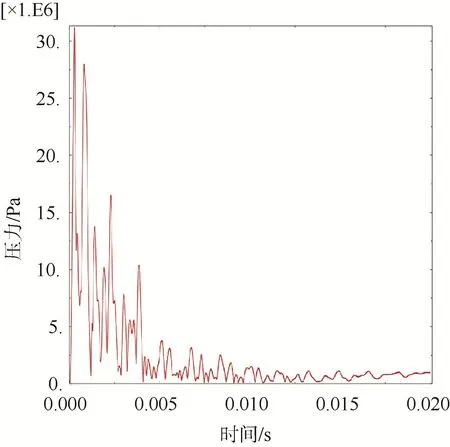
图6 远端观测点应力Fig.6 Stress profile at far-end observation point
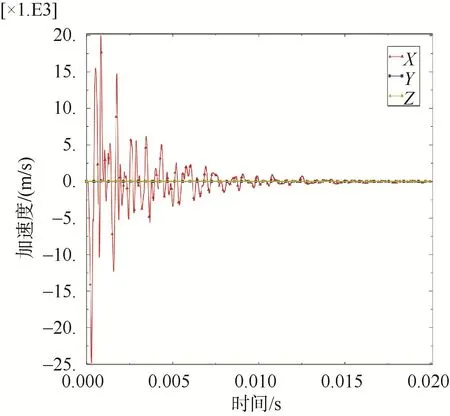
图7 迎爆面观测点加速度Fig.7 Acceleration profile at observation point on leading surface

图8 背爆面观测点加速度Fig.8 Acceleration profile at observation point on trailing surface
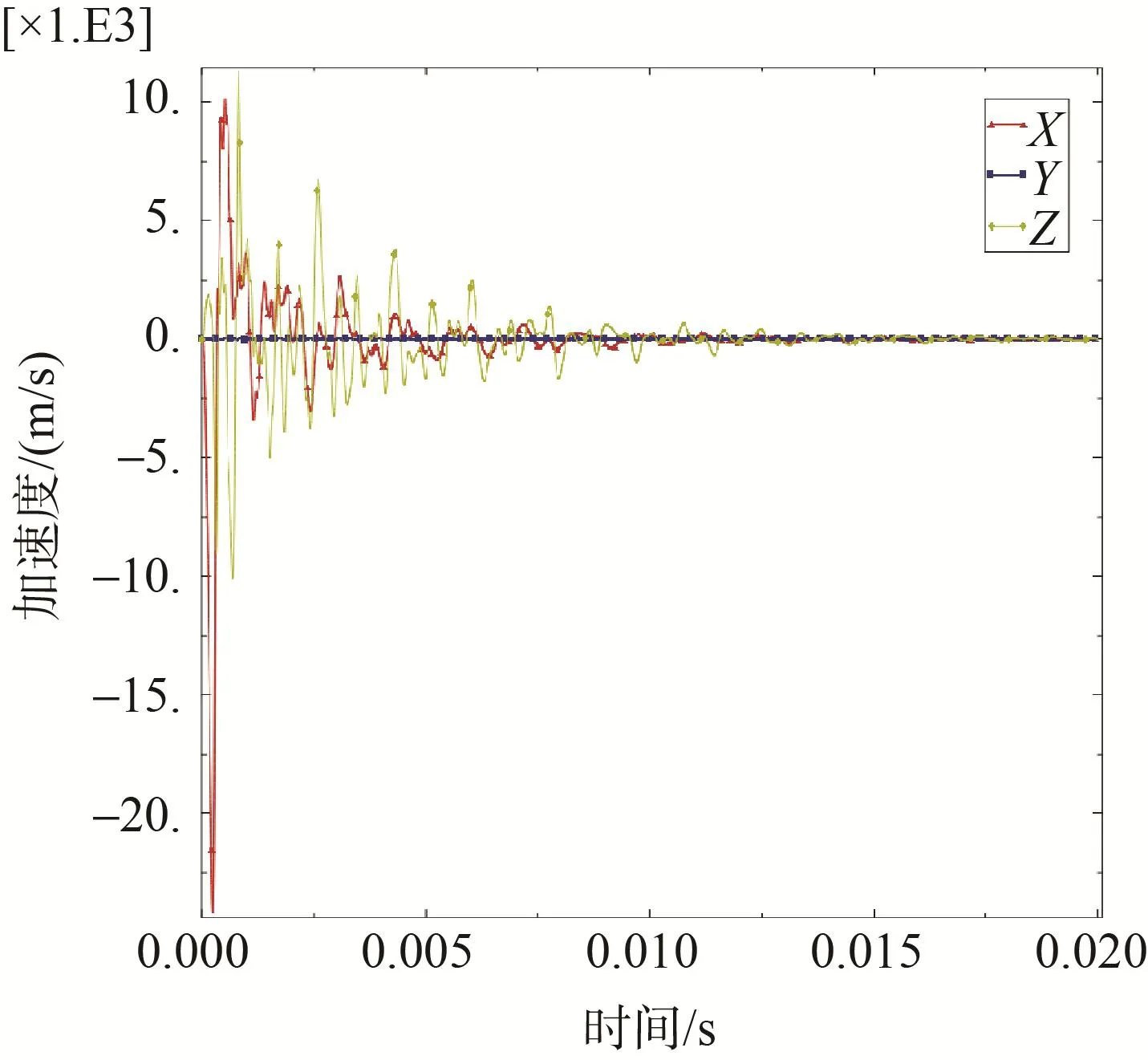
图9 侧爆面观测点加速度Fig.9 Acceleration profile at observation point on side surface
结果显示:圆筒迎爆面、侧爆面、背爆面观测点应力相继出现峰值,反映了水下冲击波的传播规律:距离爆源越近,则所受应力也越大。圆筒迎爆面距离爆源最近,所受应力最大,远端距离爆源最远,所受应力最小,侧爆面和背爆面应力介于二者之间。
圆筒各位置观测点加速度分布同样反映了水下冲击波的传播规律:距离爆源越近,则所受加速度绝对峰值也越大。
加速度3个方向分量呈现以下特点:
1)在迎爆面和背爆面区域,加速度以 x(圆筒正对爆源)方向为主,初始时刻迅速达到峰值,又迅速随时间衰减,其余2个方向加速度很小,说明迎爆面和背爆面主要受冲击波的直接作用;
2)在侧爆面区域,x和z方向加速度相继出现峰值,且峰值大小基本相当;衰减过程,z方向加速度衰减速度小于x方向;y方向加速度全程很小。说明在初始时刻,侧爆面首先受到冲击波的作用,随后,迎爆面受到的冲击使圆筒产生水平方向(z向)变形,侧面受到水平方向的挤压膨胀,进而z方向加速度迅速达到峰值;衰减过程,由于受到力传递持续作用,z向加速度衰减速度小于x方向。
3)在远端区域,x和y方向加速度相继出现峰值,且峰值大小基本相当;衰减过程,y方向加速度衰减速度小于x方向;z方向加速度全程很小。说明在初始时刻,远端首先受到冲击波的作用,随后,靠近爆源区域受到的冲击响应在圆筒上产生传递,圆筒水平方向(z向)的变形受到壳体的阻碍,阻碍作用使得z向加速度急剧消减,而在轴线方向两端无约束,y向加速度迅速传递至远端。衰减过程,由于受到y向传递持续作用,y向加速度衰减速度小于x方向。
4 透水圆筒水下爆炸有限元分析
4.1 有限元建模
透水圆筒模型的建立,参照建立密封圆筒有限元模型的方法,建立相同的外部流场模型,圆筒模型和所布置观测点不变,直接在密封圆筒模型中加入内部水域模型进行声固耦合,内部水域也采用声学单元模拟。内部水域模型见图11。

图11 内部水域有限元模型Fig.11 Finite element model of inside fluid
4.2 计算结果
透水圆筒迎爆面、背爆面、侧面以及远端观测点应力时程曲线见图12-15,加速度时程曲线见图16-19。
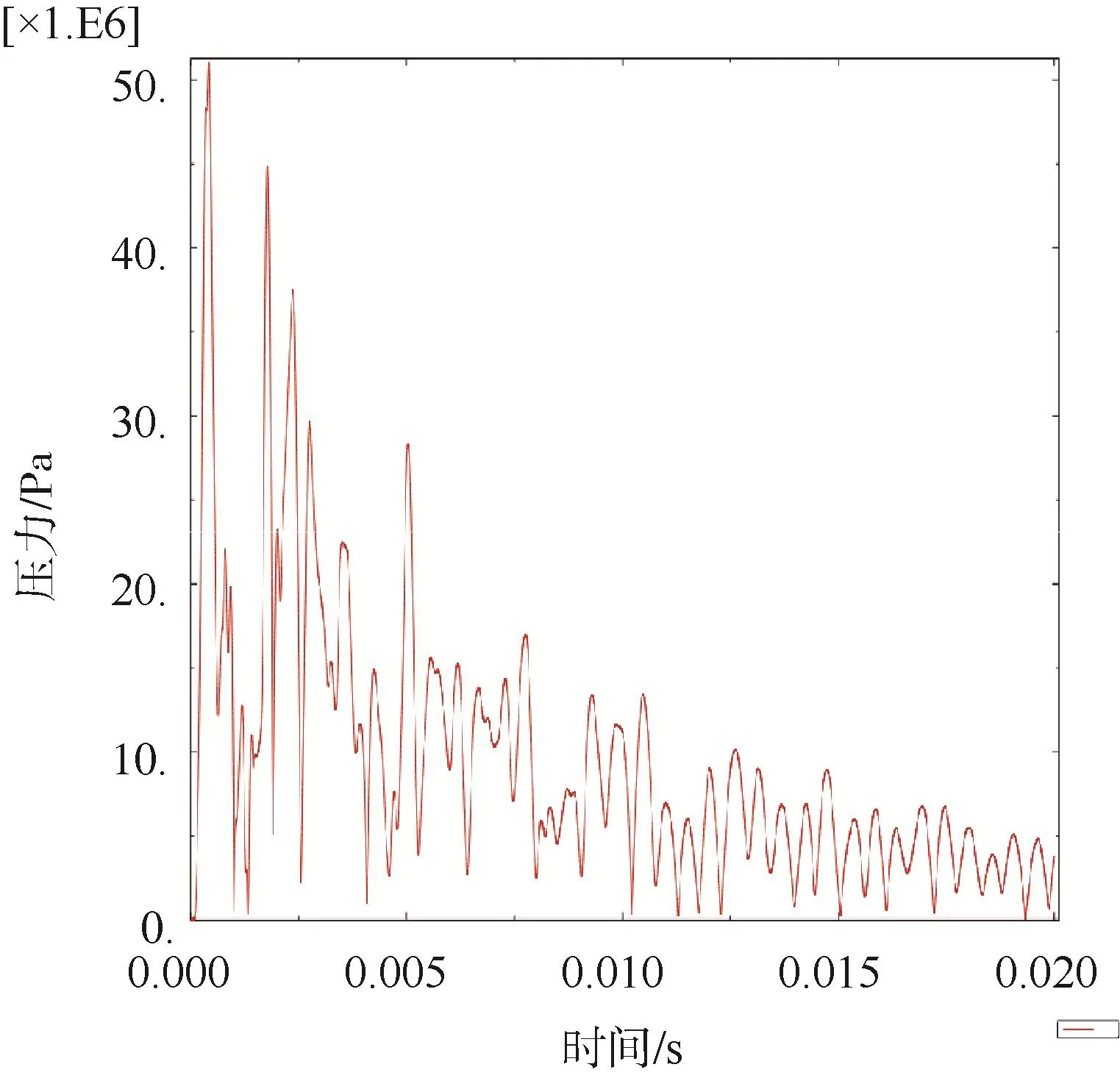
图12 迎爆面观测点应力Fig.12 Stress profile at observation point on leading surface
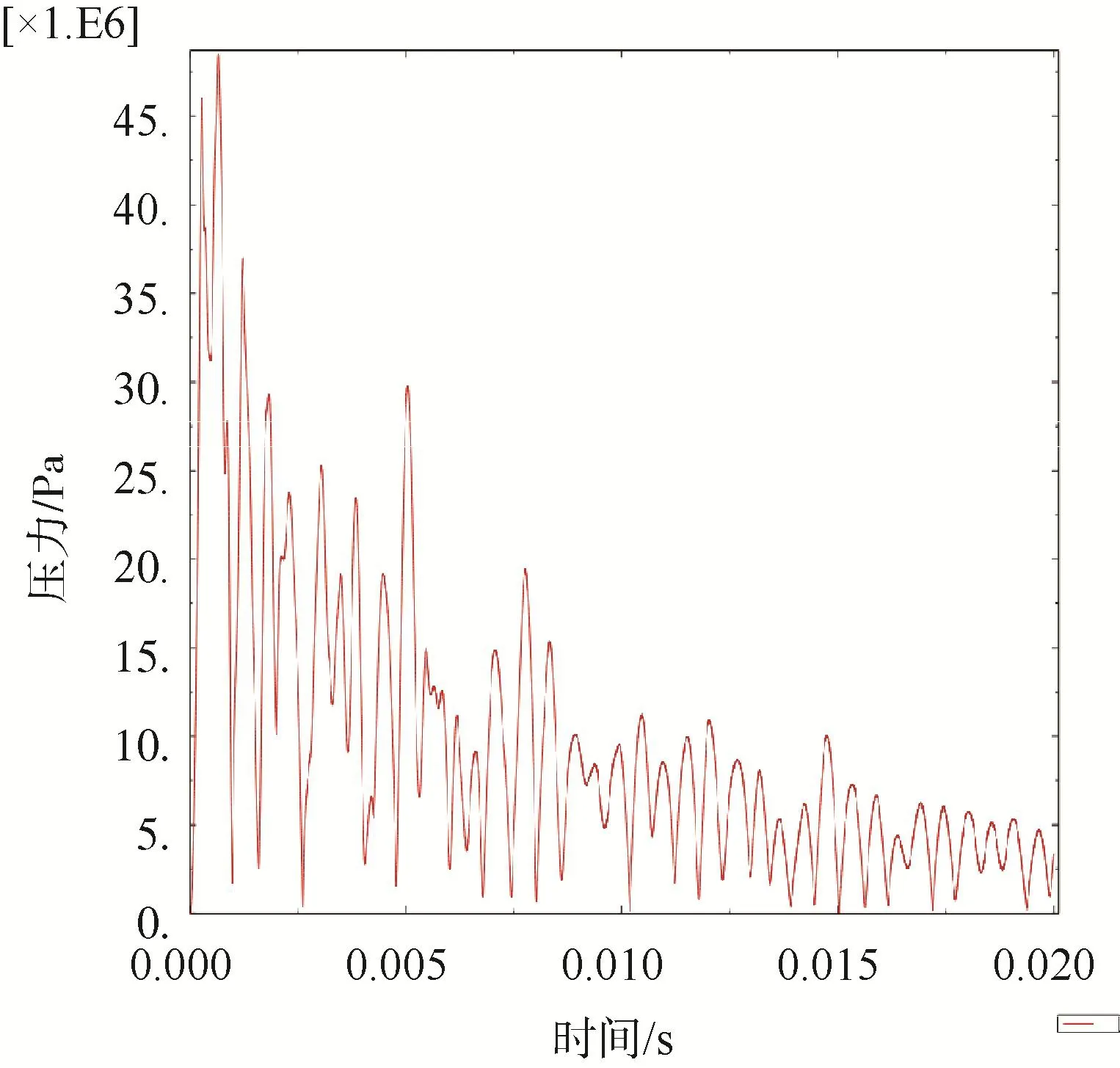
图13 背爆面观测点应力Fig.13 Stress profile at observation point on trailing surface

图14 侧爆面观测点应力Fig.14 Stress profile at observation point on side surface
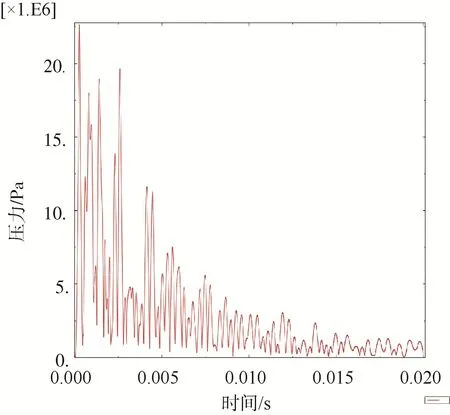
图15 远端观测点应力Fig.15 Stress profile at far-end observation point
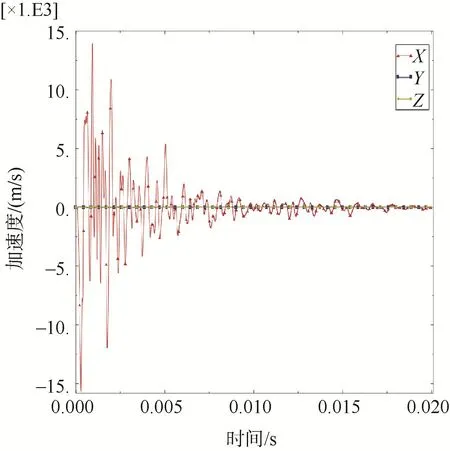
图16 迎爆面观测点加速度Fig.16 Acceleration profile at observation point on leading surface
由计算结果可知,透水圆筒各观测点应力变化趋势基本与密封圆筒一致,但是各观测点应力峰值有明显的减小,应力峰值减小了5~10 MPa,但应力随时间的衰减频率在增大。
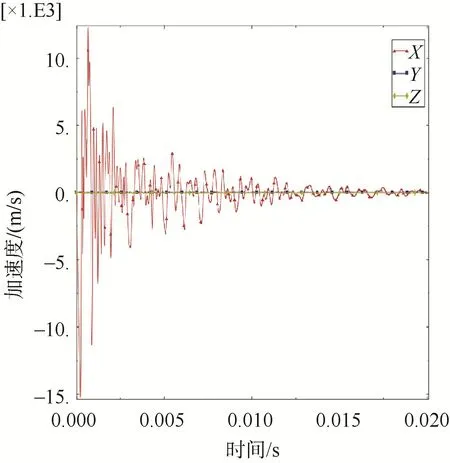
图17 背爆面观测点加速度Fig.17 Acceleration profile at observation point on trailing surface
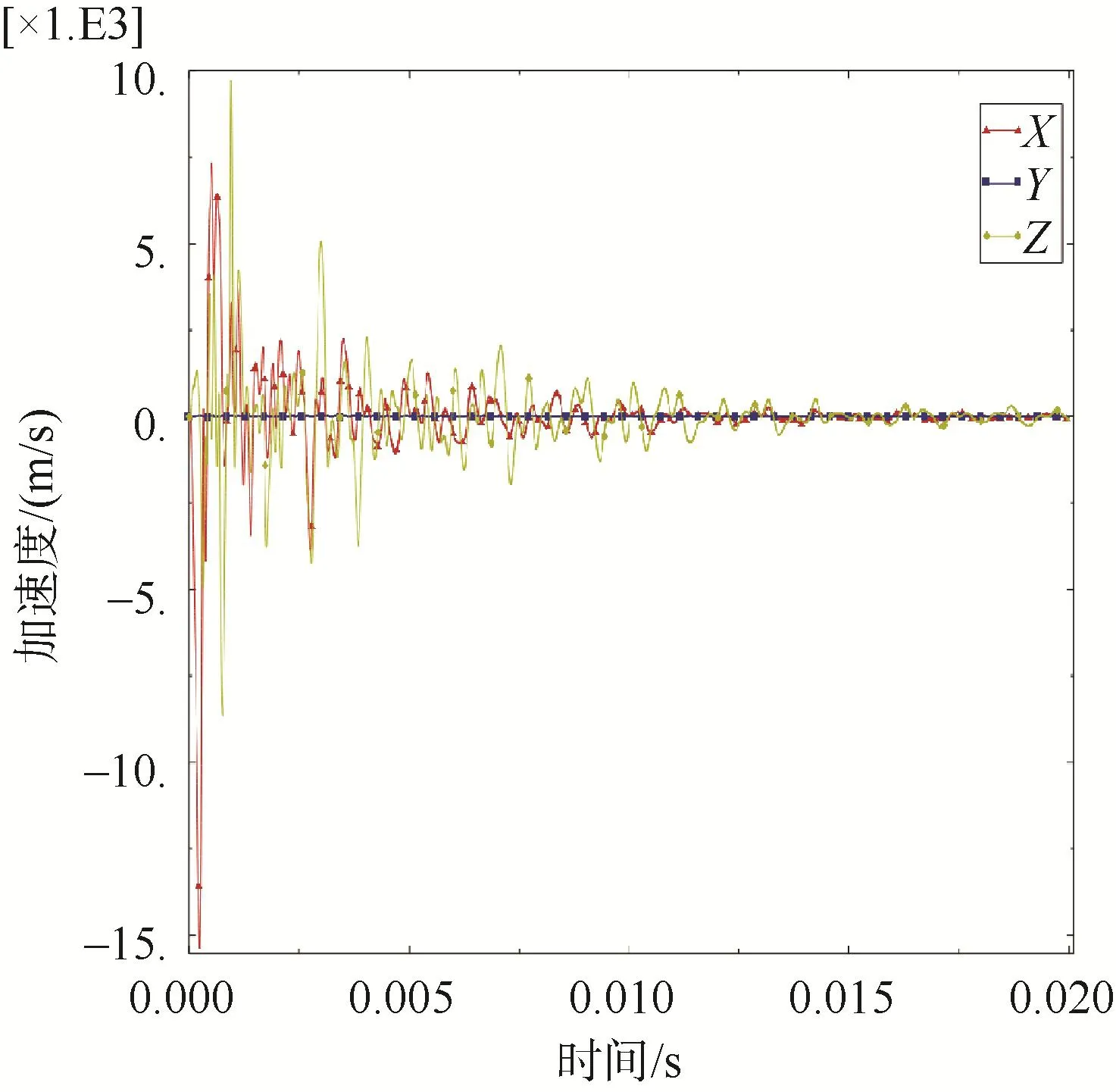
图18 侧爆面观测点加速度Fig.18 Acceleration profile at observation point on side surface
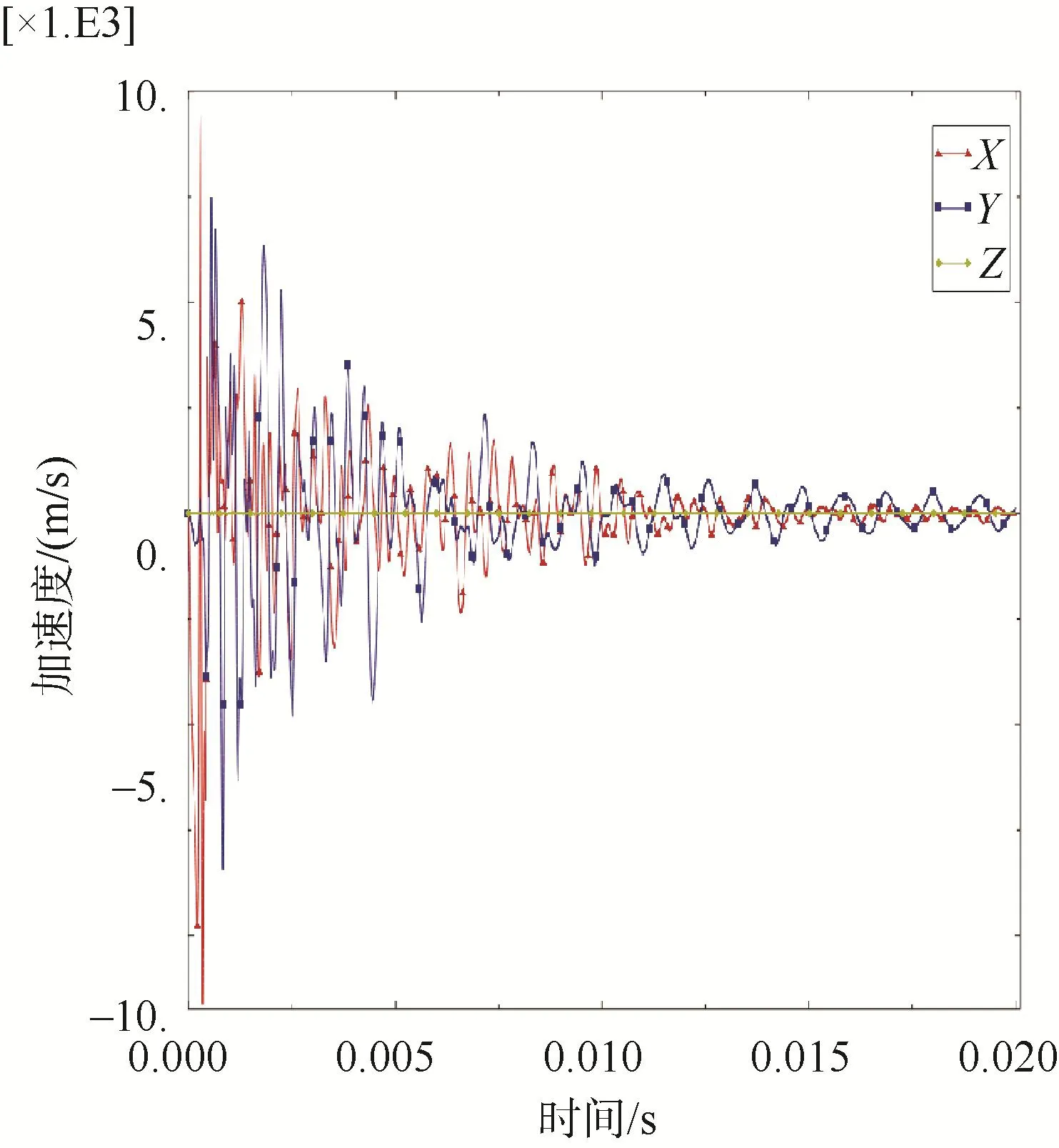
图19 远端观测点加速度Fig.19 Acceleration profile at far-end observation point
透水圆筒各观测点加速度变化趋势基本与密封圆筒一致,但各观测点加速度峰值大小在减小,加速度峰值减小了约5 000~10 000 m/s2,加速度随时间的衰减频率同样在增大。
4.3 结果比较
水下爆炸冲击与密封圆筒比较,圆筒透水后不会改变圆筒结构整体的应力以及加速度的分布趋势,但能减小结构的应力和加速度峰值大小,具有更好的抗爆炸和抗冲击性能。
5 结束语
通过利用ABAQUS软件,采用声固耦合计算方法计算圆筒冲击波压力,并与理论公式分析比较;分别对密封圆筒与透水圆筒水下爆炸模型进行计算分析,得到了圆筒不同部位的冲击响应,将二者进行对比分析,得到以下结论。
1)采用 ABAQUS声固耦合计算方法可以有效对结构进行水下爆炸分析,对工程运用提供参考;
2)圆筒迎爆面应力和加速度峰值最大,远端距离爆源最远,峰值最小,侧爆面和背爆面应力介于二者之间。圆筒各位置应力及加速度分布规律反映了水下冲击波的传播规律:距离爆源越近,所受应力和加速度峰值也越大。
3)圆筒各位置加速度分量有所不同,反映了不同位置受到的不同力的作用形式:迎爆面和背爆面主要受冲击波的直接作用,侧爆面受到冲击波和迎爆面产生水平方向变形共同作用,远端则受到冲击波和轴向加速度传递的共同作用。
4)透水圆筒与密封圆筒相比,不会改变结构整体的应力以及加速度的分布趋势,但能减小结构的应力和加速度,具有更好的抗爆炸和抗冲击性能。
