基于频域分析的间接式胎压监测算法研究

尹龙川，凃玲英，丰励，曾李，曲元君

（湖北工业大学 电气与电子工程学院，湖北 武汉 430068）

0 引言

轮胎安全是影响驾驶安全的重要因素，在行驶过程中一旦发生爆胎极易引起严重的交通事故，而轮胎压力与温度的异常是造成爆胎的主要原因。因此胎压监测对汽车安全具有重要意义[1]。

目前，胎压监测方法主要分为直接式与间接式。直接式胎压监测系统比较成熟，能够获得各个轮胎气压的准确数值，响应时间短，但成本较高，需额外在轮胎上安装压力传感器[1]；间接式胎压监测系统发展较晚，精度有待提高，但其成本较低，耐用性强，无需对轮胎改装，有着广阔的发展前景[2]。目前较为常见的间接式胎压监测算法主要有以下三种：

1）半径分析法。通过轮胎滚动半径估算轮胎气压，目前国内乘用车间接式胎压监测基本上采用此方法。但是该系统存在一定局限性，无法识别具体欠压轮胎，并且在4个轮胎都欠压的状态下，该算法无法识别[3]。

2）扭转刚度分析法。通过胎压与轮胎扭转刚度关系估计胎压状况。虽然该算法精度较高，但计算量过大，难以达到实时监控胎压状态的要求[4]。

3）频域法。利用轮胎共振频率与其压力间的特性估计轮胎气压状况，轮胎压力越高，其共振频率越大[5]。该方法对ABS轮速传感器获取的轮速信号采用传统谱估计法估计出功率谱，然后采用曲线平滑的方法提取常压与欠压时轮胎共振频率，并以此设定轮胎欠压阈值，在汽车行驶过程中动态判断轮胎是否欠压。由于频域法基于每个轮胎本身特征，因此可以独立监视特定轮胎压力，但目前的频域法准确度较低，主要是由轮速信号获取误差以及轮胎共振频率估计误差造成。因此本文从以下两个角度对算法进行改进：首先采用改进递归最小二乘法（RLS）对轮速信号进行修正，以获得准确的轮速信号；采用基于AR模型的伯格（Burg）算法代替传统谱估计进行频域分析与共振频率提取。

1 基于改进RLS的齿圈误差识别与轮速修正

1.1 轮速信号的误差分析

ABS轮速传感器如图1所示，由一个齿环和一个电磁传感器组成。

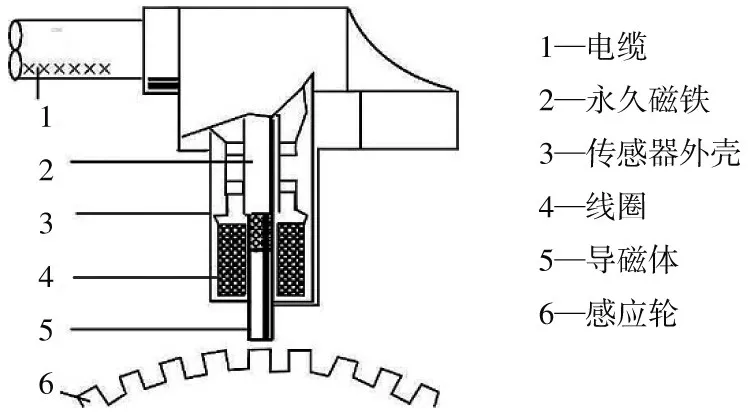
图1 ABS轮速传感器结构图

通过测量齿圈每个齿旋转过电磁传感器的时间计算出轮速：

式中：θ为每个齿的角度；r为轮胎旋转半径；t为对应齿圈旋转过电磁传感器的时间。

式中N为齿圈齿的数量。

系统时间误差与齿圈加工误差是造成ABS轮速传感器误差的主要原因。系统时间误差是由电路中计时器精度造成的，相对于齿圈加工误差，该误差可忽略[6]。齿圈加工误差是由生产或使用过程中齿圈不均匀现象导致的。该误差导致各齿角度不均，进而影响轮速计算的准确性。对平稳原始轮速信号进行谱估计，对比各速度下谱估计结果，如图2所示。结果表明，轮胎共振频率与车速具有明显线性关系。分析可知，车速增大，ABS传感器旋转频率增强，传感器测量误差增大，导致共振频率出现偏移。

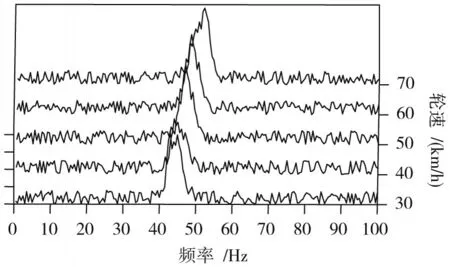
图2 原始轮速信号谱估计结果对比

1.2 改进递归最小二乘法

齿圈加工误差导致轮速计算准确性较低，因此需识别出各齿圈误差。由于汽车行驶过程中齿圈旋转较快，可认为齿圈在旋转一圈过程中近似匀速，齿圈每转过一圈，便可得到各个齿角度的一个观测值。此观测值通过近似计算得到，并不能直接运用，但可通过观测值估计齿圈角度误差值进而精确计算轮速信号。递归最小二乘法（RLS）是一种最小二乘的递归算法，具有优异的未知参数跟踪能力和快速收敛性能，能够通过一系列观测值得到参数的估计值[7]，因此可以应用在齿圈角度误差估计中。

在该算法中，信息量随着时间逐渐增大，新数据往往容易被旧数据覆盖，因此需要引进遗忘因子以弥补算法后期修正能力不足的缺陷。遗忘因子越大，算法的再适应能力越强，稳定性越弱；遗忘因子越小，算法的再适应能力越弱，稳定性越强。在实际应用中，为得到最优结果，往往期望算法在前期具有较好的再适应能力以扩大搜索范围，在后期更具稳定性以获得更好的收敛性。本文设计一种具有动态遗忘因子的RLS算法，在算法前期较大，后期较小。

RLS的基本推导本文不再赘述，具体见文献[7]，动态遗忘因子γ(n)设计如下：

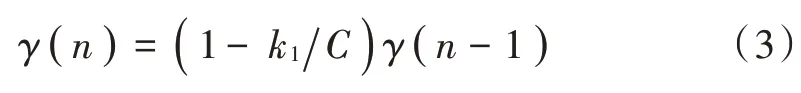
式中：C为样本数据量；k1为控制系数，以此控制遗忘因子减小的速度，本文取0.5。将动态遗忘因子插入RLS算法过程中，得到改进RLS算法步骤如下：

1）初始化参数

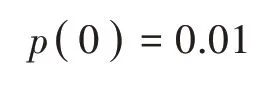
2）迭代更新

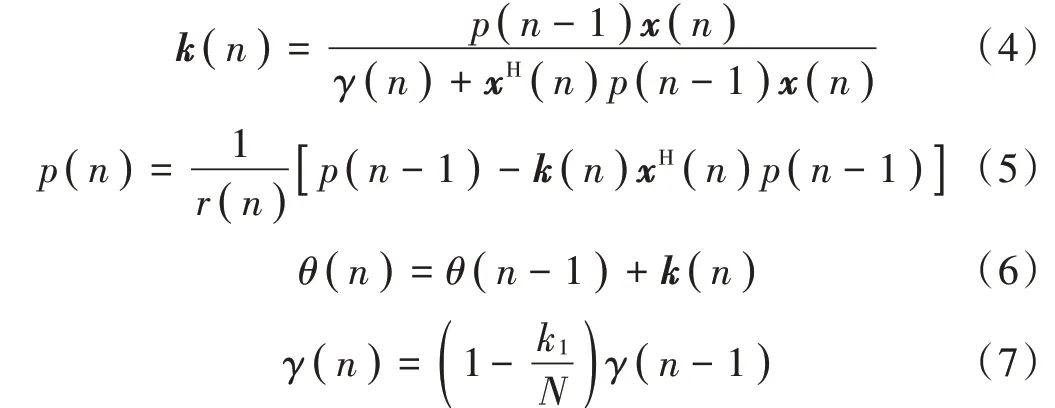
式中：N为齿圈数量；x(n)为输入参数；k(n)为增益向量；p(n)为递归因子；γ(n)为动态遗忘因子；θ(n)为估计值。

3）判断θ(n)-θ(n-1)是否小于δ（δ取极小正数），若是，输出θ(n)，若否，返回步骤2）。

1.3 齿圈误差识别与轮速修正模型的建立

对于齿数为N的齿圈，设圈数为j，齿数为i，将第j圈的第i个齿通过电磁传感器的时间记为t(i,j)。齿圈误差识别模型如下：

齿圈转过一圈的平均角速度为：

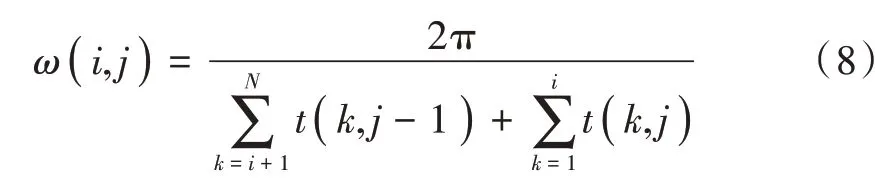
各个齿的角度测量值为：

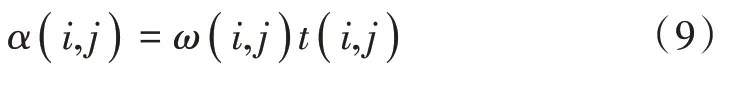
各个齿的理想角度值为：

第i个齿第j圈角度误差的测量值为：

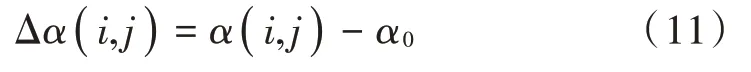
得到齿圈每一圈各个齿的角度误差测量值后，采用改进递归最小二乘法进行误差识别，估计齿圈各个齿的角度误差。设第i个齿的第j个角度误差估计值为θ(i,j)，测量值与估计值之间的差值为：

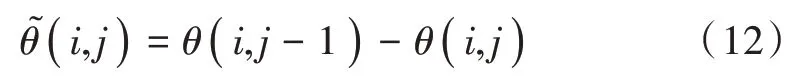
θ(i,j)值通过式（2）~式（6）更新，当时，误差收敛，输出θ(i,j)，通过N次计算，得到N个齿的误差估计值。这里取α为一极小正数。

齿圈误差估计的流程图如图3所示。

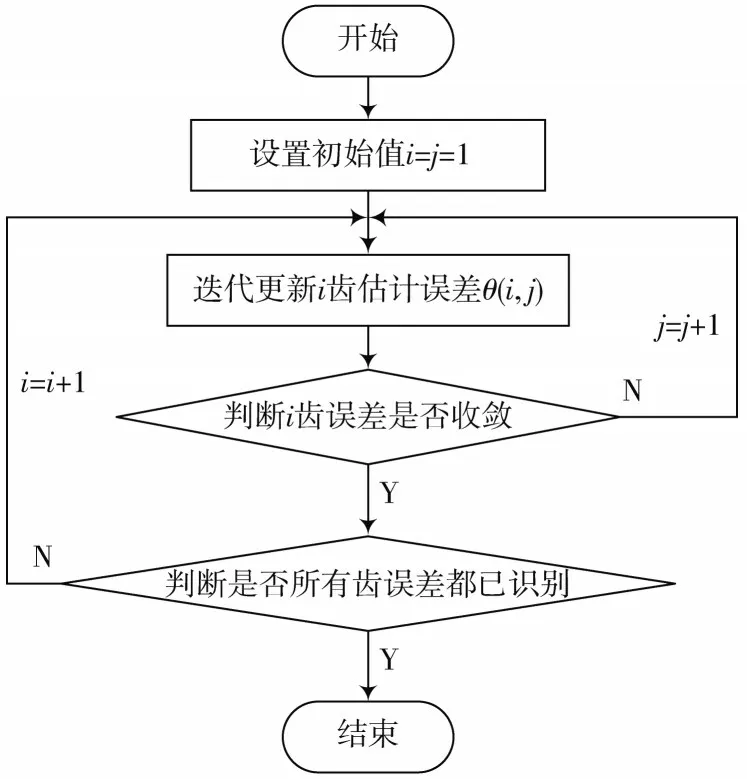
图3 齿圈误差估计流程图

估计每个齿的误差之后，通过式（13），式（14）计算出准确的轮速。

误差修正后第j圈的第i个齿通过电磁传感器的时间为：

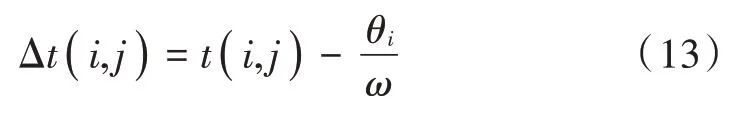
式中：θi为上文估计出的i齿角度误差；ω为齿圈平均角速度。

误差修正后轮速值为：

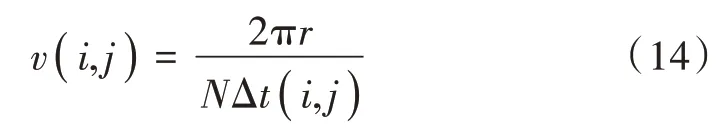
式中：r为轮胎转动半径；N为齿圈数量。

1.4 齿圈误差识别结果分析

为验证改进RLS算法的有效性，从同一轮胎原始轮速数据中选取的两组数据，应用改进RLS算法与原始RLS算法进行对比，图4和图5为两种不同算法的齿圈误差识别结果。

图4 原始RLS齿圈误差识别结果

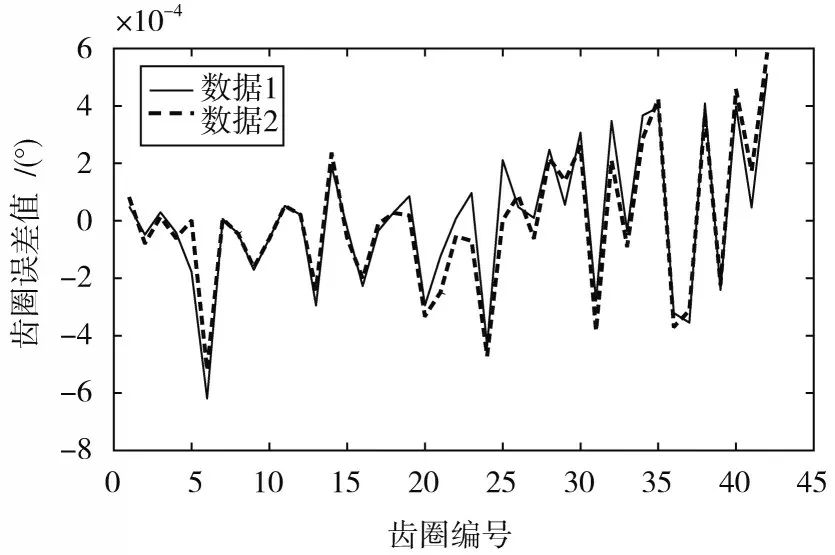
图5 改进RLS齿圈误差识别结果

利用方差衡量两组结果的偏离程度，方差值越小，偏离程度越低，算法稳定性越高。根据原始RLS算法得到的两组齿圈角度误差，计算出方差值为1.6×10-8，改进RLS算法为9×10-9。改进递归最小二乘法较原始算法增强了稳定性，更有利于后文共振频率的提取。

对修正后的轮速信号进行谱估计，对比各速度下谱估计结果，如图6所示。从图中可以看出，通过改进RLS算法消除齿圈误差并修正轮速后，轮胎共振频率与车速不再呈线性关系，说明改进RLS算法能够精准识别齿圈误差，进而修正轮速。

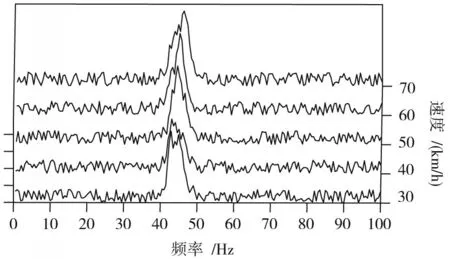
图6 修正轮速信号谱估计结果对比

2 基于频域特性的共振频率识别

目前谱估计方法分为经典谱估计与现代谱估计，经典谱估计由于其算法简单而应用广泛，但在某些精度要求较高的场合，它往往无法达到要求[7]。经典谱估计功率谱定义为：

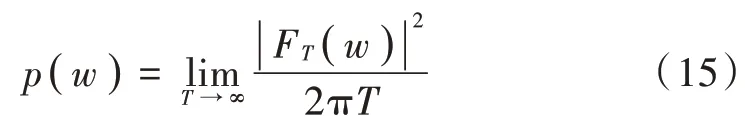
式中FT(w)为输入信号的FFT变换。从式（15）可知，经典谱估计法将功率谱定义在整个时间域，但在现实中不可能获取到整个时间域上的信号，因此使用FFT进行谱估计时会将除观察值之外的值都当作0来处理，这样在进行谱估计时会产生较大的误差。

现代谱估计法通过输入数据建立参数模型，将功率谱估计问题转换为求解模型参数问题[8-9]，无需对未知数据做出假设，准确性得到较大提升。本文选择现代谱估计中的AR模型（自回归模型）进行功率谱估计，并采用Burg算 法进行参 数估计[10-11]。

2.1 基于AR模型的Burg算法

AR模型指模型当前的输出为过去n个输出的加权和。对于随机序列的p阶AR模型，当前输出值为：

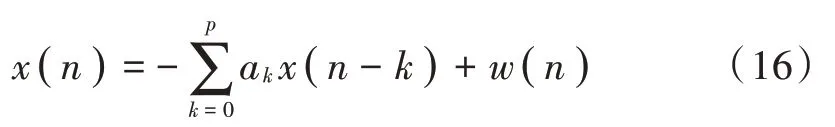
式中：w(n)是均值为0、方差为ρ的白噪声；ak为AR模型的参数。

AR模型的传递函数为：

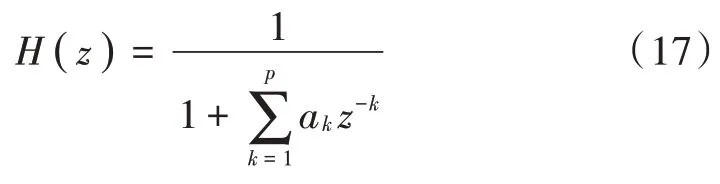
式中ρ为噪声方差。

通过推导，可得x(n)的自相关函数为：

通过上述方法，便可将求取功率谱问题转换为参数估计问题，只需确定模型阶数p、模型参数ak以及噪声方差ρ，功率谱便可直接求出。

2.2 AR模型参数计算

Burg是一种递归算法，可以根据观察数据计算出AR模型的参数。使前后预测误差的平均功率最小来计算反射系数km，进而得到模型参数。

具体计算步骤如下：

2）令m=1，计算反射系数km。

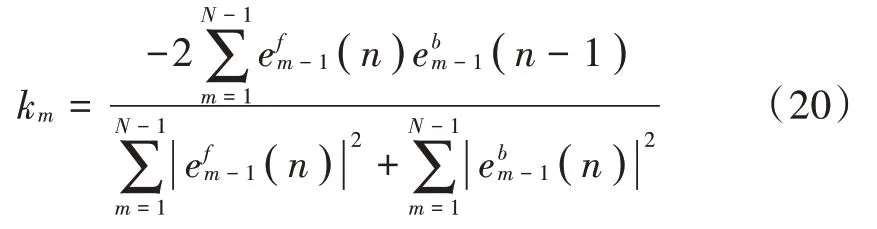
通过km计算ρ的初始值。

3）由k1的值，得出：

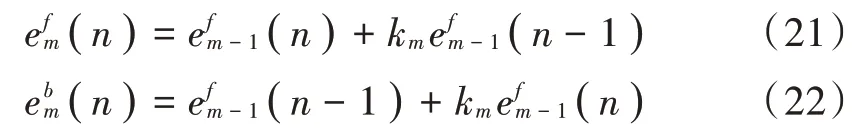
4）由递归公式计算am(k)以及ρm。

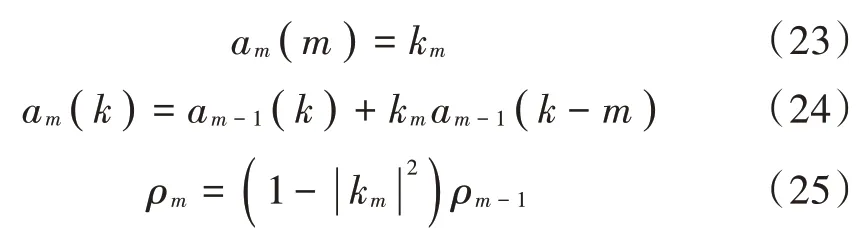
5）令m加1，重复步骤1）~步骤4），直到m=p，求出所有AR模型参数，使用式（18）估算出功率谱。

2.3 AR模型的阶

AR模型阶数对谱估计结果影响较大。阶数过低，会导致功率谱的分辨率较低；阶数过高，谱估计曲线会出现谱峰分裂，难以准确估计共振频率。阶数的合适选择可改善功率谱估计性能。目前，估算模型阶数的方法有很多[12]，但都存在一定误差，本文考虑到算法复杂度不高，因此直接采用仿真实验确定模型阶数。任意选取一组通过改进RLS算法修正齿圈误差后的轮速数据，设置不同的AR模型阶数，采用基于AR模型的Burg算法对数据进行谱估计，结果如图7所示。

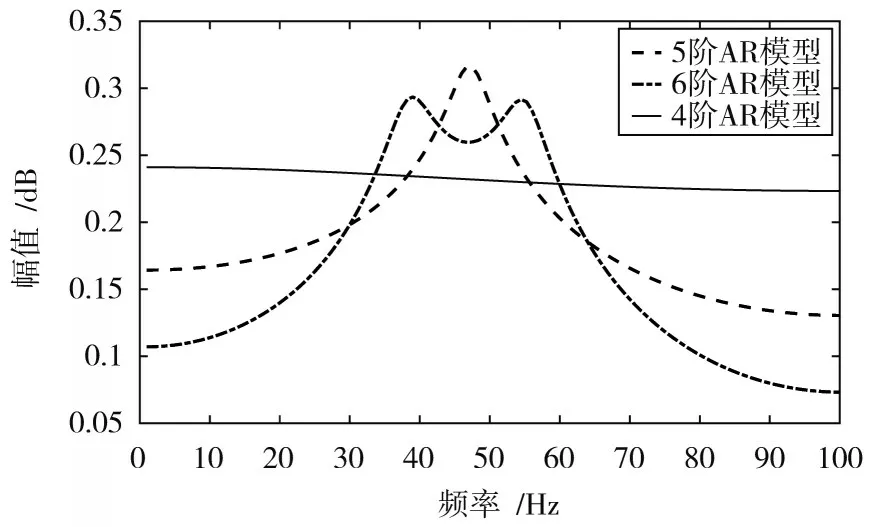
图7 AR模型阶数对比图

从图7中可知，4阶AR模型的功率谱曲线过于平滑，无法准确估计出共振频率，而6阶AR模型功率谱曲线出现了明显的谱峰分裂，5阶AR模型有着较好的估计结果。因此本文选取AR模型阶数为5。

2.4 共振频率识别结果分析

对修正后的轮速数据直接使用经典谱估计法得出功率谱如图8所示。基于AR模型的Burg算法得出的功率谱结果如图9所示。

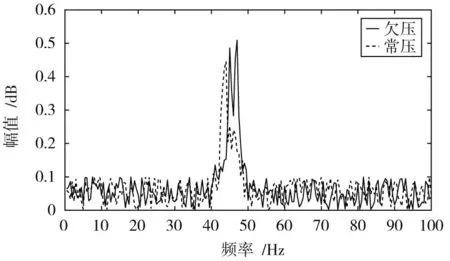
图8 经典谱估计图

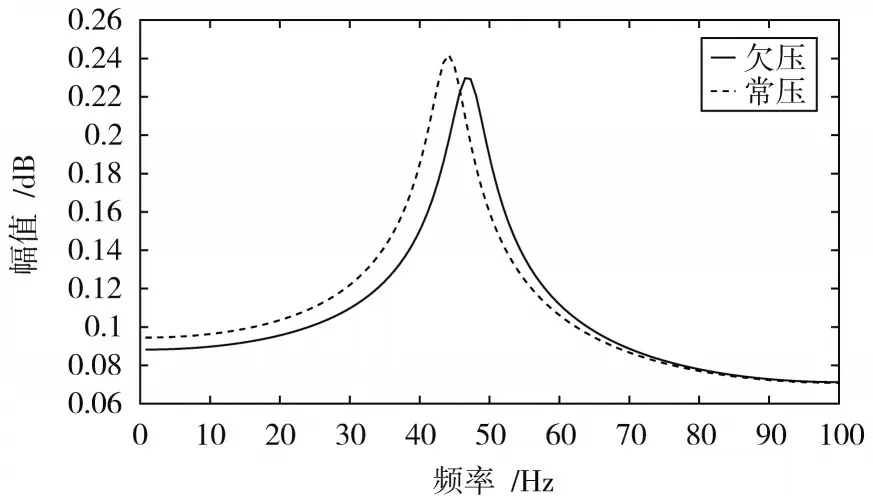
图9 基于AR模型谱估计图

从图8可知，使用经典谱估计得出功率谱平滑度较低，曲线出现毛刺甚至假峰，不能直接提取共振频率，需采用曲线平滑的方式估计共振频率[13]，影响了共振频率提取的准确性。从图9可知，基于AR模型的Burg算法得出的功率谱较为平滑，可以直接提取出共振频率，使共振频率提取结果更准确。

基于10组修正后的轮速信号，应用经典谱和基于AR模型的Burg算法分别提取10组数据的共振频率，并求得10个共振频率的平均值与方差，如表1和表2所示。

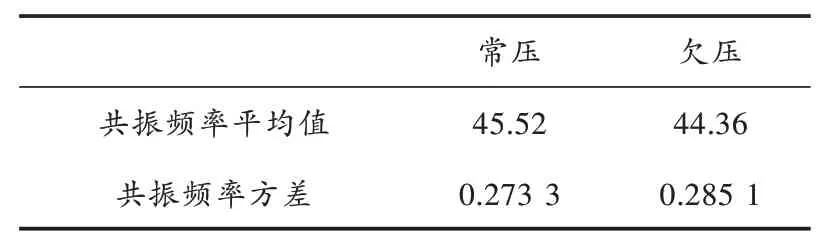
表1 经典谱估计法共振频率结果分析Hz

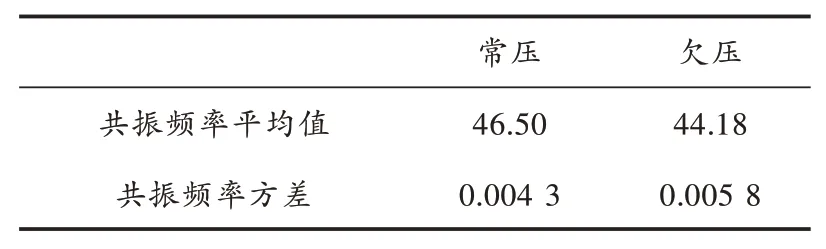
表2 基于AR谱估计共振频率结果分析Hz

从表1与表2可知，基于AR模型的谱估计提取共振频率方差性能较好，稳定性好，且常压与欠压共振频率差值较大，有利于欠压阈值的选取，更准确地判断轮胎欠压状态。

3 仿真分析

为验证该算法的有效性，在稳定条件下通过汽车自带的ABS轮速传感器对轮速信号进行获取，并使用Matlab软件对其进行仿真分析。轮速获取条件如下：

1）轮速信号的获取在平整且干燥的路段进行；

2）测量单个轮胎欠压（左前轮）时当前轮胎轮速信号，以及4个轮胎欠压时左前轮轮速信号；

3）车辆平稳驾驶，在速度为20~100 km/h之间变速行驶，未进行急加速或急减速；

4）轮胎常压设定为2.3 bar，欠压设定为1.8 bar；

5）单次测试时间为600 s。

胎压监测算法运行仿真分为欠压阈值的设定和实时胎压监控两个阶段。其中，阈值设定为：

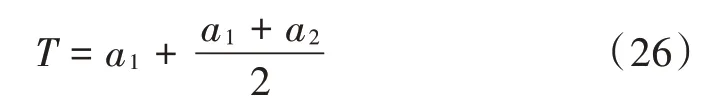
式中：a1为常压共振频率平均值；a2为欠压共振频率平均值。

最后利用ABS传感器测得的轮速信号对轮胎进行动态监测。

3.1 原始频域法胎压监测仿真分析

根据经典谱估计方法提取共振频率值，阈值设定为45 Hz，高于或等于此频率判为常压，低于此频率判为欠压。动态监测结果如图10所示，监测时间为10 min。

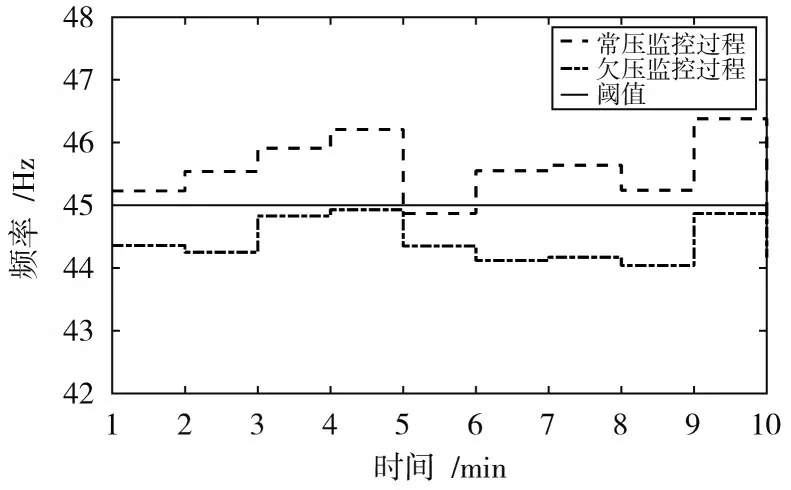
图10 原始频域法动态胎压监测图

3.2 改进频域法胎压监测仿真分析

基于AR模型的谱估计提取共振频率，阈值设定为45.5 Hz，高于或等于此频率判为常压，低于此频率判为欠压。动态监测结果如图11所示，监测时间为10 min。

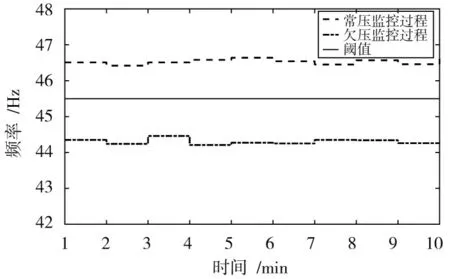
图11 改进频域法动态胎压监测图

3.3 结果分析

从图10与图11可知，原始频域法在判断胎压状态时会出现欠压频率大于常压频率的情况，缺乏准确性和稳定性，不符合胎压监测要求。改进频域法常压与欠压频率值较稳定，准确性与稳定性较高，能够很好地满足胎压监测要求。

4 结语

使用频域法对胎压进行监测的最大问题是精度不高，容易出现误判。本文设计了一种改进频域法识别胎压状态。首先识别齿圈的制造误差并以此修正轮速信号，采用基于AR模型的Burg算法对轮速信号进行功率谱分析并提取轮胎共振频率，以此为依据设置欠压阈值判别轮胎状态。本文通过轮速数据验证算法的有效性，结果表明，改进频域法较原始频域法而言准确性与稳定性有较大提升。

注：本文通讯作者为丰励。