静定结构支座反力的求解
2021-11-03苗生龙赵园园郑玉莹王秋分
苗生龙,谢 伟,赵园园,郑玉莹,王秋分
(中国矿业大学 徐海学院,江苏 徐州 221008)
静定结构的内力分析是《结构力学》的主要任务之一,而支座反力的求解则是静定结构进行内力分析的前提。多数现行教材中对支座反力的求解采用列静力平衡方程的方法,常表述为:根据解题需要对结构整体或对结构任一局部甚至某一结点建立平衡方程求解[1-4]。但有些情况下(如支座反力多于3个),如果盲目选择研究对象罗列平衡方程,可能出现联立方程组数量多而不便求解全部未知力的情况。而且静定结构种类多样,分梁、刚架、拱、桁架等,因此,对该知识点的归纳梳理显得十分重要。
本文结合静定结构的受力分析,详细阐明了支座反力求解的一般思路,归纳整理了相关类型,形成了一种通用的解决所有静定结构支座反力求解的方法。
1 常见约束的类型及受力分析
要进行支座反力求解,第一步就要对结构进行受力分析,要想正确的进行受力分析,必须对约束的类型及约束反力标注有深刻的理解并熟练掌握[5]。先对约束所产生的约束个数进行讨论,常见的约束类型可分为以下几种:第一柔性体约束,一个约束;第二光滑接触面约束,一个约束;第三固定铰、中间铰约束,两个约束;第四可动铰约束,一个约束;第五固定端、刚节点约束,3个约束;第六定向支座约束,两个约束;第七链杆约束,一个约束。
熟练掌握以上几种约束的性质后,还需要对结构进行正确的受力分析。受力分析的一般步骤为:第一解除约束,取隔离体;第二画主动力;第三在解除约束的地方代之以相应的约束力。受力分析对后续求解支座反力时快速正确的选择研究对象至关重要。
2 支座反力求解的一般思路
静定结构支座反力的求解一般采用列平衡方程的方法,而平衡方程有三种表达方式,分别为:

以上三种平衡方程在应用时需根据题目具体条件来进行选择(求解时不解或少解联立方程组,尽量一个方程求解一个未知力)。对于平面任意力系的每个研究对象,均只能列出3个独立的平衡方程,求出3个未知力,任何第4个方程都是前3个方程的线性组合,是不独立的。因此当某研究对象(常见于物体系统)上未知力的数量多于3个时,必须增加独立方程的数量才能求出相应的未知力。
如何增加独立方程数量呢?唯一的办法即是增加研究对象的数量,因为每增加一个研究对象,即可增加3个独立的平衡方程。如何才能增加研究对象数量呢?答案是断开约束,但若随意断开约束,可能对于分析问题并无益处。如图1所示,取整体为研究对象时,研究对象数目为1个,即整体,未知力有4个(A处为固定铰,有2个约束力,B、D处均为可动铰约束,分别有1个约束力),独立平衡方程数量有3个,平衡方程数量不足,未知力无法全部求出,需要增加平衡方程数量,即需要增加研究对象数量。若从B处断开,研究对象分别为AB、BD两个,独立平衡方程数量变为6个,但由于断开处约束为刚节点,其未知力有3个,总的未知力增加为7个,依然无法全部求出所有未知力,因此,需要正确地选择研究对象,即合理地选择断开约束的位置。

图1 多跨连续梁一
一般来说,为了有效增加独立平衡方程的数量,断开位置处的约束力不能超过2个,这样,断开一次,研究对象增加1个,独立的平衡方程增加3个,而未知力的增加不超过2个。若从C处断开,研究对象为AC和CD,独立的平衡方程总数为6,未知力为4+2=6个(式中数字2为C处中间铰的约束力数量),未知力即可由方程全部求解。由此可知,在选取研究对象的时候,一定要从约束力不超过3的约束处断开(常见中间铰约束处、定向支座约束处)。
3 支座反力求解的三种类型
对于一般结构来说,通常可以分为上、中、下三部分,即结构本身部分(上部)、大地或基础部分(下部)及连接这两部分的支座部分(中部),如图2所示。结构形式千变万化,但基本都是由这三部分组成的。考虑到支座(即中部)的不同,从求支座反力的角度看,大致可以分为三种类型。
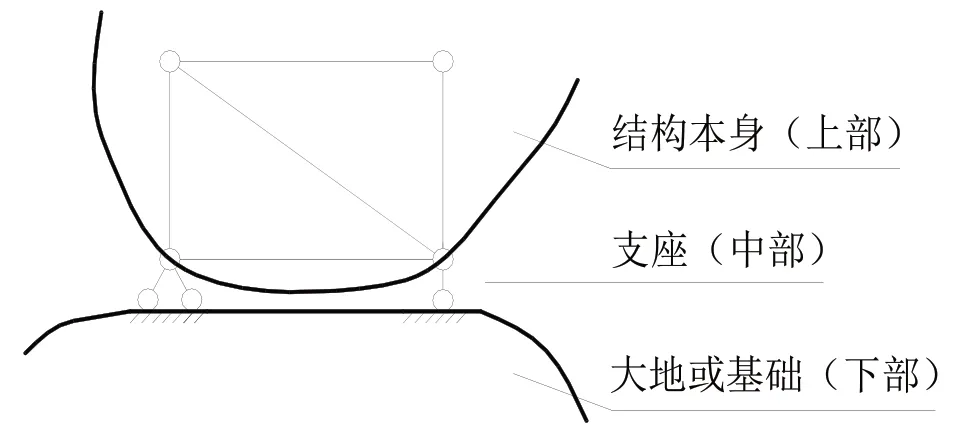
图2 平面体系组成
3.1 类型一
如图3(a)所示结构,该结构体系的支座反力为3个,取上部结构本身AC为研究对象(如图3(b)所示),列三个平衡方程即可求出所有的支座反力,考虑到尽量一个方程解一个未知力的原则,平衡方程可按如下顺序罗列:

图3 类型一

此种类型为求支座反力类型中最简单的一类,即结构全部的支座反力只有3个。
3.2 类型二
如图1所示结构,该结构体系的支座反力有4个,若取上部结构ABCD为研究对象,方程数量不足,无法求出全部支座反力,必须增加研究对象数量,从而增加平衡方程数量。为此需要切断约束。前述已经讨论过,需要从约束力少于3的地方断开,即只能从C处(中间铰,2个约束力)断开,研究对象分别为AC、CD,受力如图4所示。

图4 类型二
先对CD部分进行受力分析(如图4(a)),有3个未知力,列如下平衡方程即可求出:

然后再对AC进行受力分析(如图4(b)),只有3个未知力(FCx=F′Cx,FCy=F′Cy),列如下平衡方程即可求出:

此种类型中,必有一个研究对象上的未知力个数不超过3个,因此从该研究对象入手,依次研究其余部分,即可求出全部支座反力。
3.3 类型三
如图5所示结构,该结构体系的中部约束即支座反力有5个,可从C、D处断开,将结构分为AC、CD和DF三部分,但每一个研究对象上的未知力均超过3个,无法用平衡方程一次性求出。经受力分析发现,CD部分的4个未知力中有三个交于C点或D点(如图5(c)所示),可采用力矩法求出FDy(MC=0);然后再对DF段进行受力分析(如图5(d)所示),则只存在3个未知力(FDy=F′Dy),可列三个平衡方程求出DF段的3个未知力,然后再研究CD段,求出其全部未知力,最后研究AC段,进而求出全部支座反力。

图5 类型三
此种类型中,所有研究对象上的未知力数量均超过3个,但至少有一个研究对象(假定其未知力个数为n)存在如下情况:至少有n-1个未知力平行或者交于一点,求解时即可从该研究对象入手,采用投影法或力矩法先求出一个或两个未知力,然后再选取其它研究对象,联立即可求出全部未知力。

4 结语
通过对各种约束性质的整理,及结构杆件的受力分析,本文阐述了静定结构求解支座反力的基本思路、方法,并将之归纳整理为三种类型,应用该分析方法可对所有类型静定结构(梁、刚架、桁架、组合结构等)进行支座反力求解。
