斜盘式轴向柱塞泵转子系统动态特性分析

冉启平，王 涛，刘 冰，董兴建

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.中国北方车辆研究所车辆传动重点实验室，北京 100072；3.上海航天控制技术研究所，上海 200240)

引言

随着液压传动技术的不断发展，高压、高速、大功率成为液压传动技术的主要方向之一[1]。斜盘式轴向柱塞泵作为一种重要的液压传动机构，与之相关的配流盘、流量方面的研究已有不少[2-4]；同时，作为典型的旋转机械，其转子系统是柱塞泵的核心。因此，研究柱塞泵转子系统的动力学特性，对柱塞泵的振动机理方面的研究具有重要意义。针对柱塞泵转子，部分学者进行相关方面的研究和分析。

郭长虹等[5]、权凌霄等[6]研究了间隙环流和支承间距对十一柱塞航空轴向泵转子系统临界转速的影响，对柱塞泵转子的设计具有指导意义；同时权凌霄等[7]还基于转子动力学和振动传递路径理论对柱塞泵的振动特性进行研究，为柱塞泵的振动机理研究奠定了基础；胡连红[8]将柱塞泵的轴承转子系统组件作为研究对象，通过有限元方法分析该转子系统的临界转速，并以此给出柱塞泵转动组件的设计意见，为实现柱塞泵精确的振动控制提供参考；权凌霄等[9]借助有限元方法得到柱塞泵主轴及缸体的临界转速，为进一步对柱塞泵转子系统进行动力学研究奠定了基础；李贾宝等[10]借助AMESim仿真平台，在考虑了液压油的有效体积弹性模量的基础上，分析了油液的含气量、温度、压力等参数对柱塞泵输入轴转速波动程度的影响规律，为轴向柱塞泵的故障诊断和状态监测等方面的研究提供了新的切入点；朱德等[11]使用ANSYS Workbench对柱塞泵主轴进行静力和模态分析，为后续的柱塞泵主轴优化设计提供了一定的参考；李奕宁等[12]对某型号轴向柱塞泵进行了振动测试试验，通过仿真和试验结果对比分析了不同转速下的柱塞泵振动噪声来源，提出了减振降噪的方案。

鉴于针对柱塞泵转子系统进行瞬态动力学方面的分析研究相对有限，本研究以斜盘式轴向柱塞泵转子系统为对象，通过有限元方法计算柱塞泵转子系统在稳态载荷下的响应，并分析了转子轴承支承特性对转子系统响应的影响，为轴向柱塞泵壳体的结构响应计算提供了基础。

1 转子模型

1.1 转子结构

转子系统作为斜盘式轴向柱塞泵的核心部件，主要由输入轴、缸体、柱塞杆、滑靴等部件构成，其结构如图1所示。

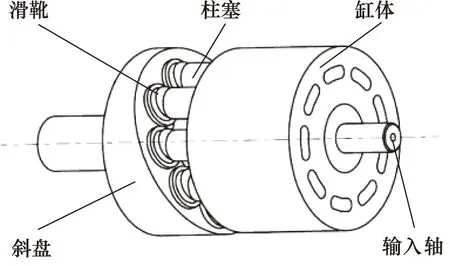
图1 柱塞泵转子模型示意图

柱塞泵工作时，外部动力源带动输入轴和缸体转动，滑靴通过与斜盘的相互作用，迫使柱塞和滑靴在跟随柱塞缸体转动的同时进行相对于柱塞缸的往复直线运动。

1.2 柱塞转动惯量分析

柱塞相对于缸体沿轴向存在往复运动，因此，需首先明确柱塞-滑靴的直线运动导致的转动惯量变化规律。

如图2所示，将柱塞运动分解为以转速ω绕转子的匀速转动和相对于缸体的往复直线运动。以斜盘中心为原点建立坐标系X，Y，Z，并假设柱塞位置处于上死点时转角为0，由运动分析可得，在该坐标系下任意柱塞杆i的滑靴的坐标为：

图2 柱塞-滑靴运动简图

(1)

对柱塞i运动分解，其往复直线运动的运动方程为：

(2)

其中,R为柱塞分布圆半径;θ=ωt为输入轴转动角度;γ为斜盘倾角。

设柱塞全长为L，滑靴质量为m，柱塞质量为M且柱塞质量沿长度均匀分布，将柱塞划分为三部分，如图2 所示。其中与滑靴相连的为第一部分，中间部分柱塞为第二部分，末段柱塞为第三部分，由式(3)，推导得第i个柱塞的第一、第二和第三部分杆长为:

(3)

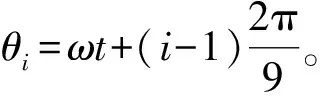
由柱塞质量均匀分布假设，得各部分柱塞质量为:

(4)

分离滑靴与柱塞，滑靴处理为一集中质量，其余三部分柱塞分别使用3个集中惯性质量替代分析，每部分柱塞集中质量位置为各部分的中点；以第一部分柱塞为例，其任意一段柱塞转动惯量如式(5)所示:

(5)

对该部分柱塞杆的X向转动惯量Ix分析有:

(6)

式(6)分为两部分：柱塞对于自身质心的转动惯量和柱塞化简至简化中心后由平行轴定理所得转动惯量。对于式(6)的第一部分和第二部分进行求和化简后得:

(7)

由式(7)知，第一部分柱塞的X向转动惯量为常数；同理，得到第一部分柱塞的Y向、Z向以及第二、三部分柱塞和滑靴的转动惯量均为常数。

1.3 柱塞-滑靴组件偏心分析

由于斜盘倾角γ不为0°，柱塞滑靴沿缸体周向并非对称分布，故转子旋转时对缸体产生偏心力，成为整个转子的偏心载荷。

以第一部分9段柱塞各段的偏心力Fei为例，参考图2中柱塞结构划分，可由式(8)计算得:

(8)

以第一部分中第一段柱塞为例，其对转子的偏心力为Fe1，对第一部分9段柱塞偏心力求和，得到第一部分柱塞对柱塞泵转子的偏心载荷Fe。第一部分柱塞偏心力结果如图3所示。

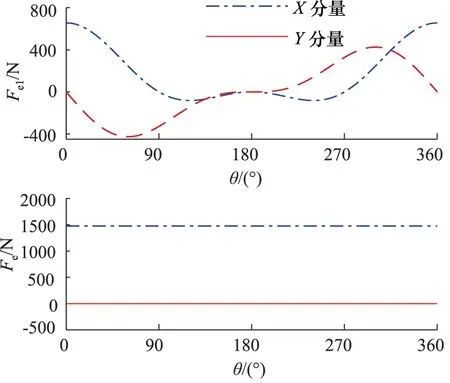
图3 第一段柱塞偏心力

由柱塞偏心力结果知，柱塞与滑靴沿转子周向的不均匀分布对转子造成偏心作用，该作用方向和大小恒定；同理可计算出第三部分柱塞对转子造成偏心作用，而第二部分柱塞为均匀分布，其9段柱塞离心力形成汇交力系，故对转子偏心力载荷为0。

1.4 柱塞泵转子支承刚度分析

柱塞泵转子使用滚动轴承支承，其支承刚度随着滚子滚动到不同位置产生周期性的变化。通常对于滚子轴承，由式(9)近似计算轴承滚动体所受最大载荷[13]：

(9)

其中,Fr为轴承所受径向载荷；KF为载荷系数，球轴承取4.73，滚子轴承取4.08；Z为轴承滚动体数量；ϑ为滚动体同滚道接触角。

假设轴承在最低点总存在1个虚滚子[14]，其在所有滚子中承担最大载荷Qmax和最大变形量δmax，但该滚子仅用于变形协调分析而不参与实际轴承载荷计算。对于滚动轴承，由接触力学得到滚子载荷Q和变形δ之间符合如下关系[13]：

Q=Klδn

(10)

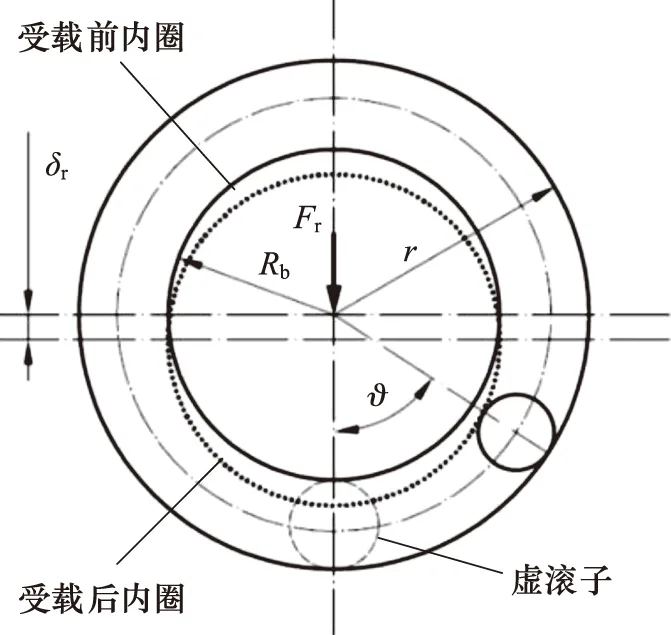
图4 虚滚子示意图

使用控制误差的迭代法进行轴承载荷和轴承变形量的求解[15]。最终使得轴承在径向载荷Fr的作用下虚滚子载荷Qmax和最大径向变形量δr在给定的误差范围内同时满足式(9)和式(10)。对轴承的滚子时间-位置进行离散化，将一个滚子公转周期划分为若干等分，对每一个等分时间点进行轴承的刚度计算，得轴承的离散化时变刚度[14]:

(11)

表1、表2分别为柱塞泵转子前轴承和尾轴承的相关参数。

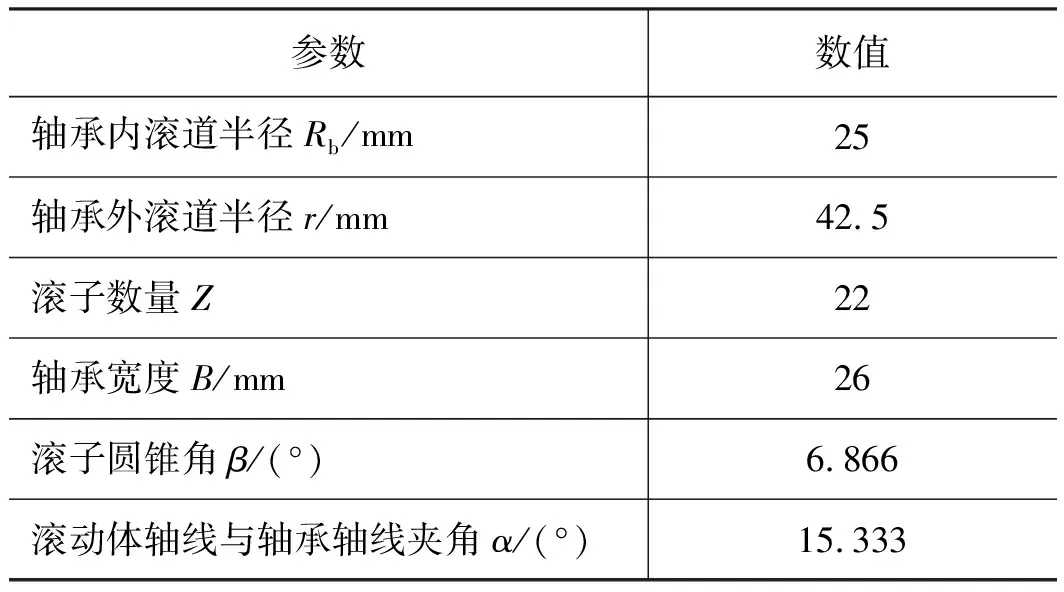
表1 前轴承参数

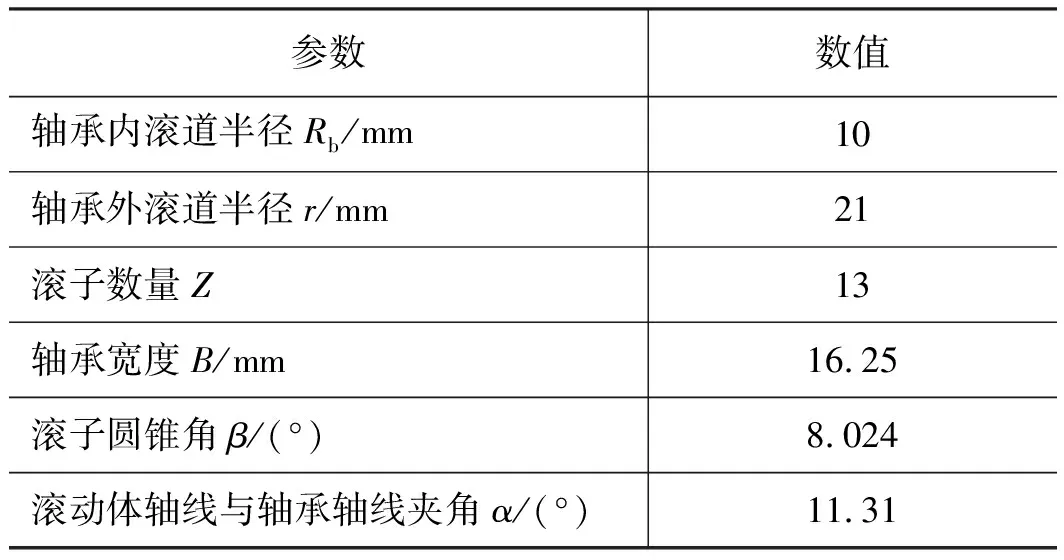
表2 尾轴承参数

由表1、表2中数据可以计算出柱塞泵转子的前轴承和尾轴承刚度变化曲线分别如图5a和图5b所示。

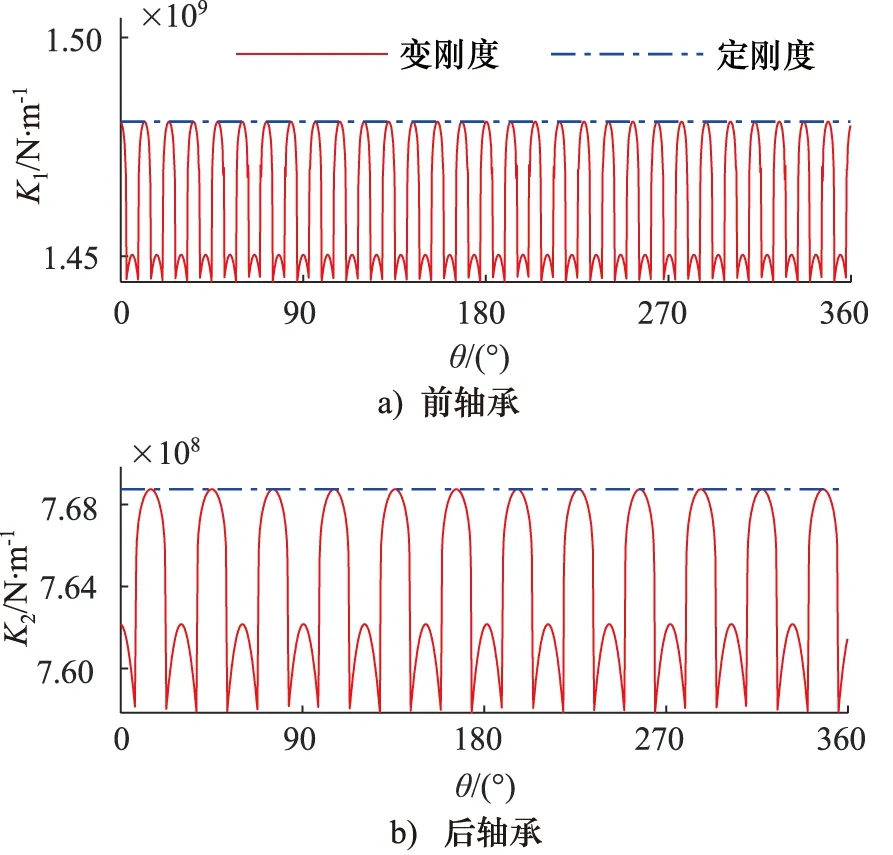
图5 轴承刚度

由计算结果知，柱塞泵转子旋转一周，前轴承支承刚度变化N1为30个周期，尾轴承支承刚度变化N2为12个周期。

1.5 转子有限元模型

柱塞泵转子主要受到两部分结构外载荷作用：斜盘对转子的载荷作用和配流盘对转子的载荷作用。

简化柱塞泵转子几何后，使用BEAM188梁单元建立转子模型，柱塞-滑靴组件的三部分使用MASS21单元代替，COMBI214单元模拟轴承支承刚度，得到柱塞泵转子有限元模型如图6所示。转子所受外载荷加载位置分别为：斜盘载荷加载位置选择靠斜盘一侧柱塞缸端面中心；配流盘载荷加载位置选择靠配流盘一侧柱塞缸端面中心。

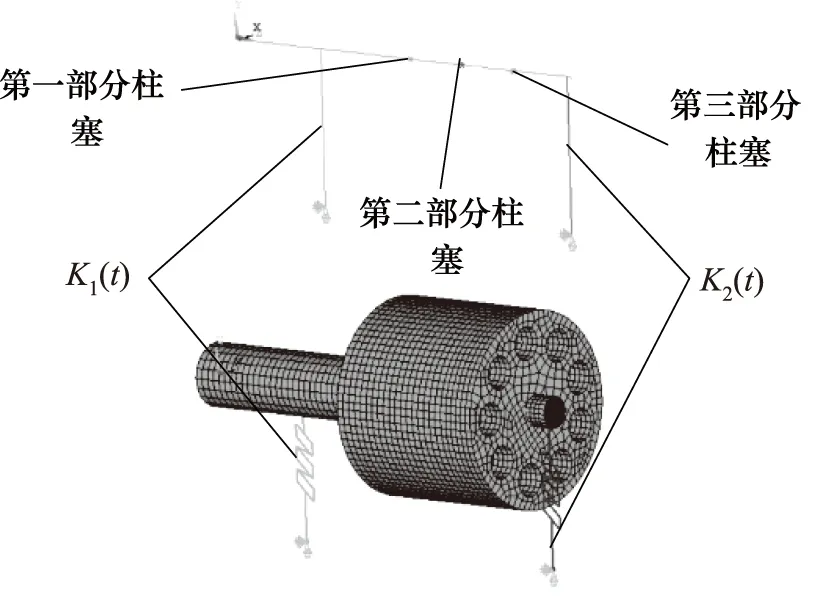
图6 转子有限元模型

2 转子外载荷分析

2.1 斜盘侧稳态载荷

如图7所示，柱塞所受力包括柱塞底部液压力Fb，回程弹簧回复力Fk，轴向往复运动导致的惯性力Fg，旋转导致的离心力Fa，斜盘对柱塞滑靴的支承力FN，柱塞与柱塞腔壁之间的接触力F1与F2以及其接触力引起的摩擦力Ff。

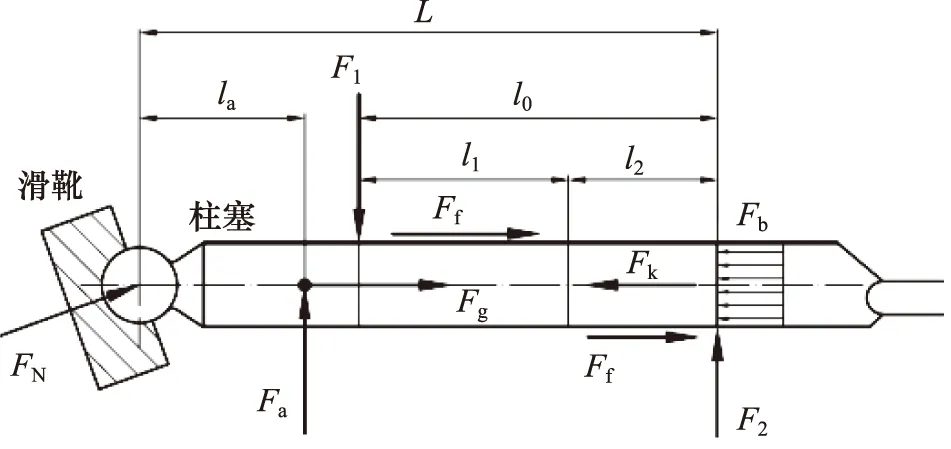
图7 柱塞受力分析示意图

在坐标系X，Y，Z下，分析柱塞所受各个力，得到柱塞的力平衡方程和力矩平衡方程分别如式(12)和式(13)所示：

(12)

(13)

其中，式(12)和式(13)中各个已知力分量如下所示。

离心力：

Fa=[-m2Rω2sinωt,m2Rω2cosωt,0]

柱塞底部液压力：

回程弹簧回复力：

Fk=[0,0,-Fk0+KRcosθtanγ]

惯性力：

Fg=[0,0,-mzω2Rtanγcosωt]

支承力：

FN=[0,FNsinγ,FNcosγ]

滑靴摩擦力：

FfN=[f1FNcosφ,f1FNsinφcosγ,

-f1FNsinφsinγ]

联立式(12)、式(13)，求解出斜盘对滑靴法向支承力FN，相关参数见柱塞泵参数表3。

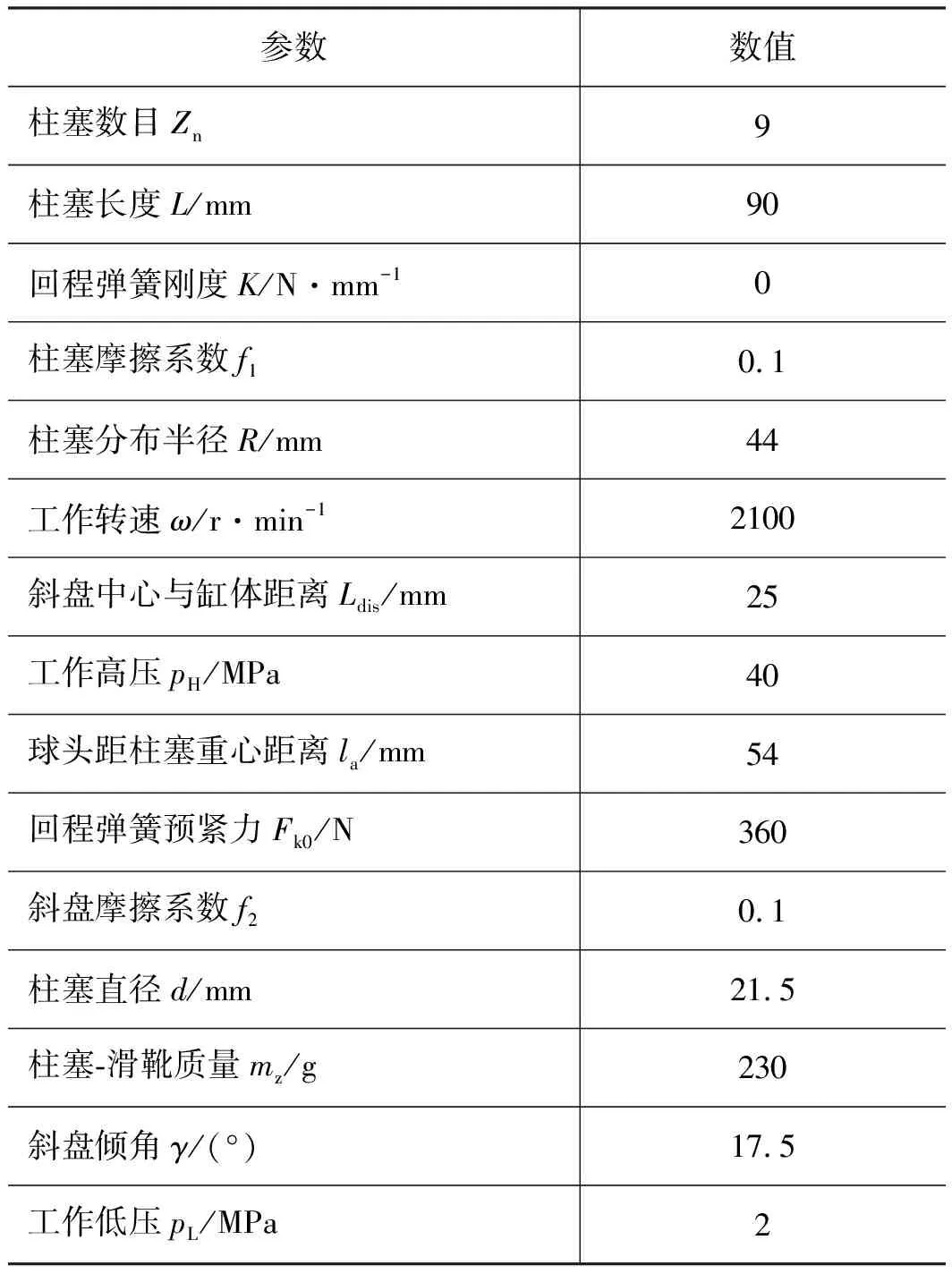
表3 柱塞泵参数

由表3中数据，计算得柱塞泵的斜盘对滑靴法向支承力FN数值结果，如图8所示。由支承力FN计算结果可知，柱塞泵的工作压力对支承力影响最大。当柱塞杆处于高压区时，斜盘对滑靴的作用力远大于柱塞杆在低压区作用力，导致柱塞泵在工作过程中的冲击现象。

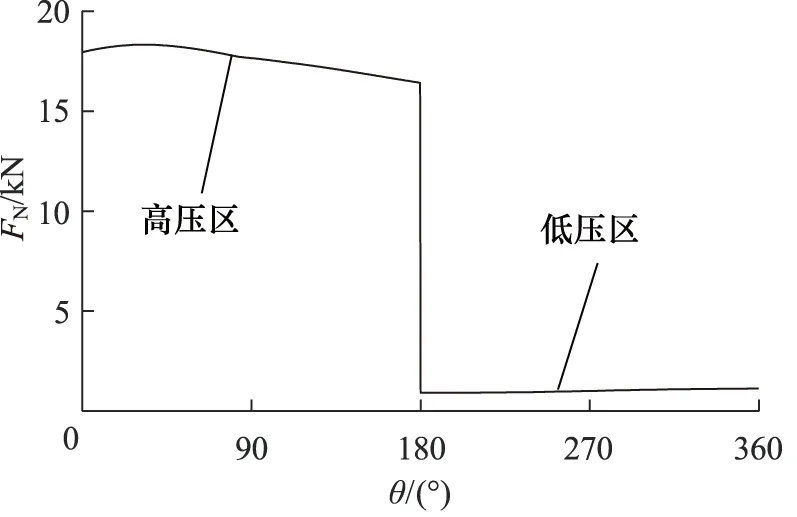
图8 滑靴法向支承力FN

坐标系X，Y，Z下，滑靴所受斜盘的作用力Fs表达式为:

Fs=[FNf1cosφ,FN(f1sinφcosγ+sinγ),

-FN(f1sinφsinγ-cosγ)]

(14)

其中,φ为滑靴在斜盘上运动的轨迹切角，如图2所示。将滑靴所受力化简至斜盘载荷作用位置，得到斜盘对柱塞泵转子的作用载荷表达式如下：

(15)

2.2 配流盘侧稳态载荷

因缸体与配流盘的间隙充满带有压力的油液，使缸体受到油压的推力作用。设pb为配流盘腰型槽内压力，R1为内密封带边界，R2为配流盘腰型槽小径，R3为配流盘腰型槽大径，R4为外密封带边界；另设配流盘上压力区包角为φ，可得配流盘对缸体油压作用力为[16]：

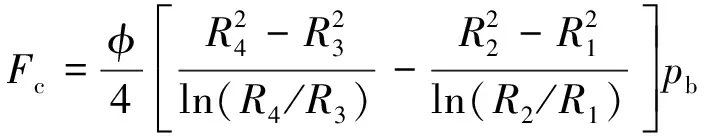
(16)

配流盘相关参数参见表4。

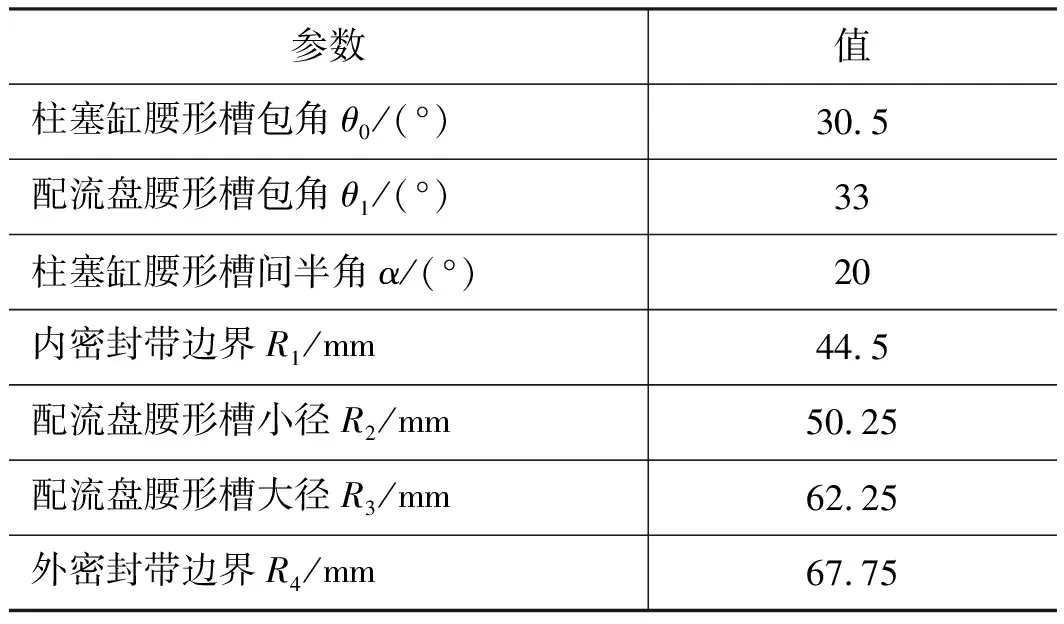
表4 柱塞泵配流盘参数

由式 (16)计算得到配流盘对缸体油压推力Fc数值结果，如图9所示。

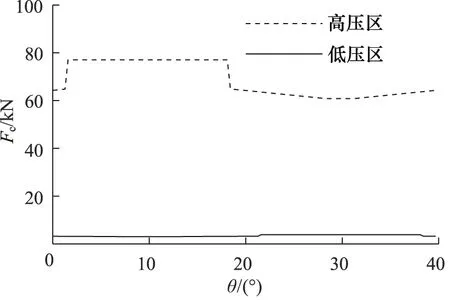
图9 配流盘推力Fc

从配流盘推力计算结果可知，缸体所受配流盘推力在高压区有较大波动，这是由于压力包角φ变化引起的；且对于高压区，因工作压力远高于低压区，使得在压力包角变化程度相同的情况下，高压区的推力波动远大于低压区。

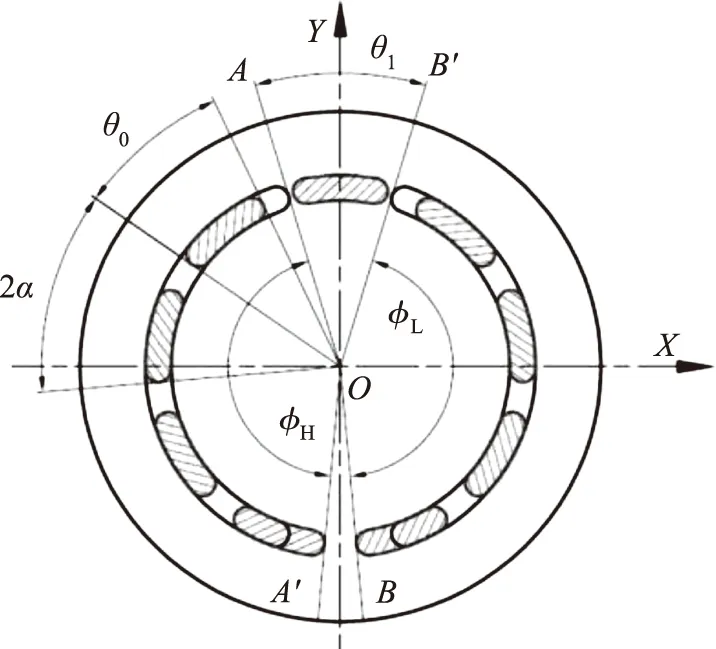
图10 柱塞泵配流盘压力包角

配流盘对缸体推力的合力作用点位置，由作用角度φ/2与作用半径R0表示，合力的作用点必然在压力包角的角平分线上，作用半径由式(17)计算得[14]:

(17)

由式(17)计算得高压区推力Fc_H和低压区推力Fc_L的作用半径RH和RL。得到配流盘对柱塞缸推力化简至配流侧加载位置后，对应载荷表达式为:

(18)

其中,Fc_H作用矢径：

[rHx,rHy,0]=[RHsin(φH/2+∠AOY),

-RHcos(φH/2+∠AOY),0]

Fc_L作用矢径：

[rLx,rLy,0]=[RLsin(φL/2+∠BOY),

-RLcos(φL/2+∠BOY),0]

2.3 转子外载荷求解

柱塞泵转子斜盘侧稳态载荷和配流盘侧稳态载荷由式(15)、式(18)计算；转子在旋转一周所受斜盘侧载荷和配流盘侧载荷如图11～图14所示。

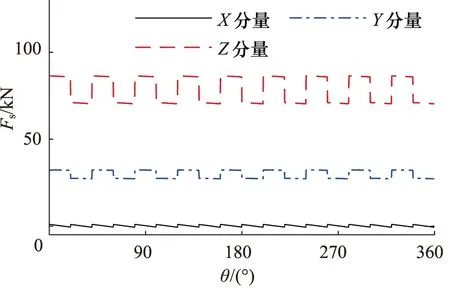
图11 斜盘侧力载荷

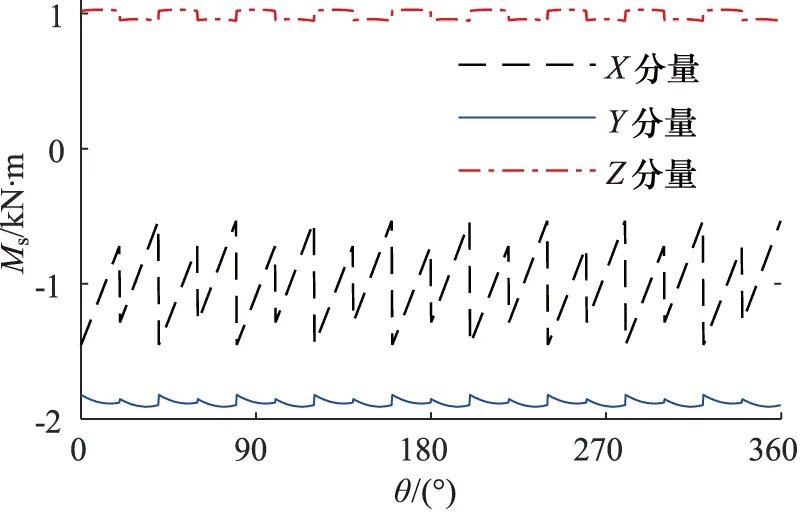
图12 斜盘侧矩载荷

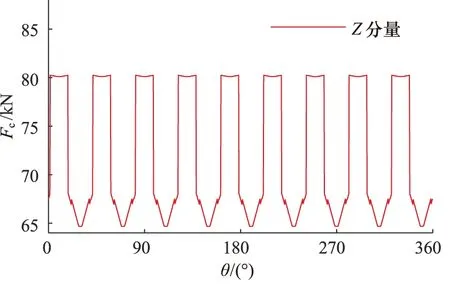
图13 配流盘侧力载荷

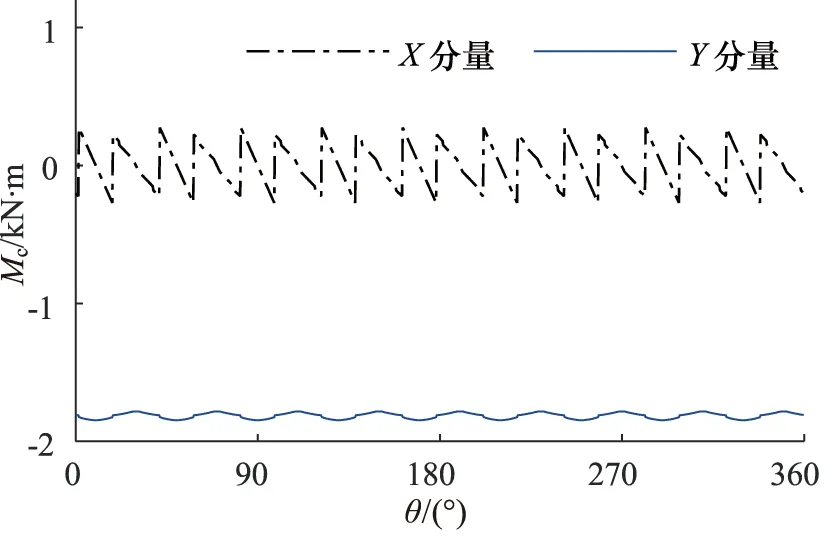
图14 配流盘侧矩载荷

由载荷结果可知，转子所受载荷在1个旋转周期内，均可分为9个更小的载荷周期，这是由于柱塞泵缸体上沿周向均布有9个柱塞，每个柱塞受到的斜盘激励仅同前一柱塞所受载荷滞后一个大小为2π/9的相位差，使柱塞泵转子所受激励频率具有9倍频率放大作用。

同时，柱塞泵的高低压区由Y轴沿Z轴方向分割，一侧高压一侧低压，而柱塞数目为奇数，导致Z方向上的力载荷会有较大波动进而对整个柱塞泵造成结构上的冲击作用，因此需重视柱塞泵在Y方向和Z方向上的支承设计。

3 柱塞泵转子稳态响应分析

在所得外载荷激励下，分别计算柱塞泵转子在定刚度和变刚度支承下的瞬态响应。以转子前轴承为例，提取轴承支承位置处X方向和Y方向上的位移响应，其结果如图15、图16所示。

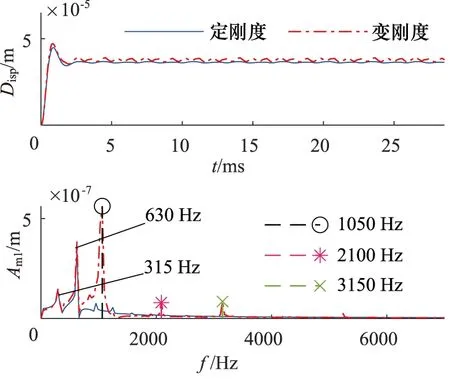
图15 前轴承X方向位移响应

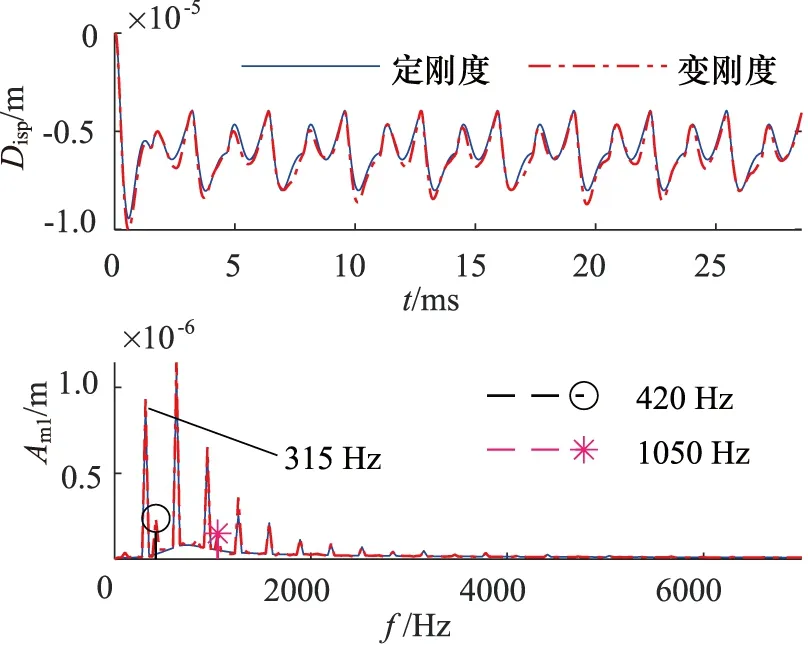
图16 前轴承Y方向位移响应

由转子响应结果可知，同定刚度转子响应相比，变刚度转子的响应结果包含轴承的调制成分。由表3可知，转子转速ω=2100 r/min，对应转频fω=35 Hz，同时由转子结构载荷分析可知，转子外载荷的基础激励频率为:

fLoad=fω×Zn

(19)

则转子所受激励频率应为fload及其倍频，其中Zn为柱塞泵缸体上柱塞个数，得到fload=315 Hz。由表5可知，柱塞泵转子旋转一周，前轴承和尾轴承支承刚度分别变化N1和N2个周期。转子稳态响应的部分频率成分同转频的关系如表5所示。

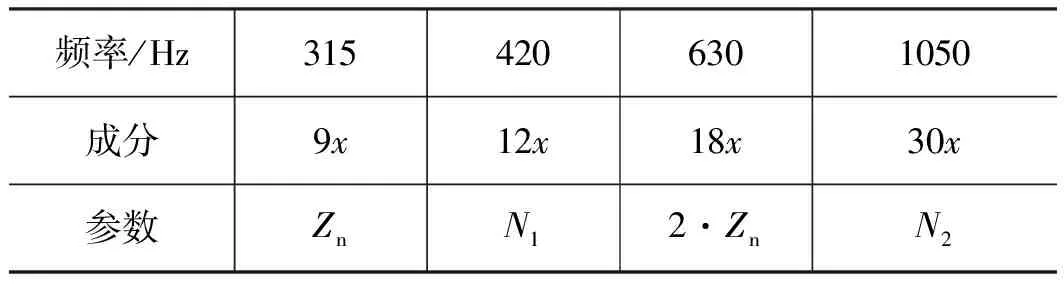
表5 变刚度支承下转子响应成分

注：x表示转子转频倍数。

对比转子部分响应结果，轴承的刚度变化直接影响柱塞泵转子的响应成分；因此，是否考虑滚动轴承的非线性特性直接决定了转子响应的频率成分，结合实际工程考虑，更为准确的柱塞泵转子响应计算需要考虑滚动轴承的非线性特征。

4 结论

(1) 在考虑斜盘倾角不为零的情况下，推导得到柱塞-滑靴组件的转动惯量为常数；并因柱塞-滑靴组件的周向非对称分布，导致其对柱塞泵转子存在偏心载荷作用，且该作用的方向和大小恒定；

(2) 轴向柱塞泵转子的支承方式大多使用滚动轴承，而转子稳态响应计算结果表明，轴承的非线性刚度特性会影响转子响应成分，在不考虑轴承非线性刚度特性时会造成转子稳态响应计算结果中丢失部分频率成分，进而削弱计算结果的准确性；

(3) 借助结构载荷代替不同部件之间的相互作用关系，将柱塞泵转子从柱塞泵整体结构中分离并计算转子稳态响应；同时，轴承反作用力为壳体所受载荷之一，其频域结果同转子转频之间的关系可作为柱塞泵壳体设计的参考之一，避免壳体发生共振。

上述研究成果为后续的柱塞泵壳体响应计算和壳体结构的拓扑优化设计奠定了基础。