创新数量、创新质量与企业效益的互动机制研究

俞立平

(浙江工商大学统计与数学学院，杭州 310018)

0 引 言

党的十九届五中全会指出我国已转向高质量发展阶段，制度优势明显，但创新能力不能适应高质量发展的要求。改革开放以来，我国一直重视科技创新的作用，科技水平和能力得到了长足的发展。目前科技论文数量已经名列全球第二，载人航天、北斗导航、高性能计算机等领域的水平已居世界前列，但与此形成巨大反差的是，我国超一流的科技成果偏少，科技对经济的支撑不足，经济发展面临转型升级的巨大压力，科技成果转化水平低，著名的钱学森之问凸显顶级科技人力资源不足，这一切充分说明了我国存在创新数量不足、创新质量不高等问题。

高技术产业是我国国民经济的主导产业和创新主体。研究高技术产业创新数量、创新质量与高技术产业效益的关系，分析不同性质的创新成果对高技术产业效益的影响机制，有利于总结高技术产业创新的特征和规律，发现存在的问题，对于高技术产业发展以及政府制定相关政策具有重要借鉴意义。

创新理论经历了从企业到产业、从微观到宏观的发展历程，逐步形成了基于产业角度研究创新的理论基础。“创新(Innovation)”的概念由Schumpeter首次提出，他在经济学中引入“创新”思想。在创新质量的定义及其效用的研究方面，Haner(2002)初步提出了一个创新质量概念框架，认为创新质量应该定义为在“潜能-过程-结果”这三个递进的维度中创新绩效的综合[1]。杨幽红(2013)从顾客满意和成本两方面出发进行定义，创新质量包括产品质量、服务质量和过程质量[2]。Bloom等(2002)研究发现引用率高的专利能有效提高企业价值[3]。

关于创新质量与绩效的关系及其实证研究，Lanjouw等(2004)以专利指标为主建立指标体系评价创新质量，研究发现创新质量对公司股票市场价值的弹性系数为正数[4]。张子娟(2013)研究发现虽然对于企业成长来说，创新并没有显著的正向作用，但提高创新质量能够加速企业发展[5]。叶子荣、贾宪洲(2011)通过知识生产函数，对我国省际动态面板数据进行建模，研究发现在发明专利这一技术创新活动中，与科技财政资金的产出弹性相比，非政府科技资金的产出弹性更高[6]。高林、贺京同和那艺(2014)研究发现创新激励对其数量与质量的影响存在异质性[7]。

根据以上对现有研究的总结来看，学界对创新质量的界定及其重要性的研究成果较为丰富。关于创新质量的作用，涉及其与公司股票市场价值、创新绩效、企业成长、创新投入、创新激励、经营绩效等的关系，研究既有宏观视角也有微观视角。从目前的研究看，有必要从以下几个方面进行深入研究：创新数量与质量两者之间的关系及其协调性，该领域的研究文献较少，需要进一步进行研究；对于创新数量、创新质量与高技术企业效益的关系，现有研究更加侧重企业效益受创新的影响程度，而对创新数量和质量所受企业效益的反馈作用这一方面研究较少；现有研究较少关注高技术产业创新质量与创新数量的相关问题，高技术产业是我国国民经济的主导产业和非常重要的创新主体，研究其创新数量、质量的相关问题具有重要价值。

本文选取的研究对象为高技术产业，首先对创新质量、创新数量作用机制进行分析，并采用面板数据模型研究两者及其共同作用对企业效益的贡献，并利用贝叶斯向量自回归模型(BVAR)对三者之间的互动关系进行研究。系统总结我国高技术产业创新现状，分析其中存在的问题，并提出相关政策建议。

1 创新数量、质量与效益之间的互动关系

创新数量、质量与效益之间的互动关系见图1。

图1 创新数量、质量与效益

创新数量与创新质量。创新的数量与质量同等重要，对高技术产业而言，没有一定的创新数量，很难保证有较高的创新质量；即使有高水平的创新质量，如果没有一定的规模，也很难推动高技术产业发展。对企业而言，除了以上内容成立以外，创新质量与创新数量有时是两者不可得兼的关系，如果研发项目投入过多、资源分散，加上高质量的项目研发投入多、周期长，在面临激烈市场竞争的情况下，往往难以保证较高的质量。当然，如果企业为了确保创新质量，往往难以兼顾数量。所以说，数量是质量的基础，质量是数量的目标。即使有较高的创新质量，但如果没有一定的数量也没有意义；而没有一定的创新数量，很难出现较高的创新质量。

创新数量、创新质量与企业效益。从微观角度来看，无论是创新数量或者是质量，对企业效益应该有显著贡献，但是这种作用并不总是存在，比如新产品研发成功，需要投入大量设备，那么短期内可能难以取得利润，何况还有创新失败的可能。从宏观产业角度，创新数量对企业效益应该产生积极的影响，这是因为大多数企业的创新总能获益，从而弥补了少数企业的波动。但创新质量的情况比较复杂，我国高技术产业创新质量总体不够高，如果没有一定的规模，有可能难以对企业效益产生积极影响。为此，本文提出假设H1：高技术产业创新数量对企业效益具有正向促进作用；H2：高技术产业创新质量对企业效益具有负向作用。

当然，高技术企业效益对创新质量、创新数量具有负向作用。如果企业效益的源泉不是创新，那么非常明显，效益对创新数量和创新质量产生不了正反馈；如果企业从创新中获益，创新数量多，创新质量高，企业往往愿意加大研发投入，从而提高创新数量和质量，形成良性循环。当然，这种提升可能是同步的，也有可能是分先后次序的，有时以提升创新质量为主，有时以提升创新数量为主。

创新数量、创新质量与投入要素的关系。投入要素包括资本和劳动力，Solow(1958)很早就开始研究技术进步与要素投入之间的关系[8]。Van Reenen(1997)基于598个英国企业的面板数据研究发现，创新对就业具有正向影响[9]。Young(2004)研究了偏向型技术进步(biased technical change)与商业周期以及劳动收入比重波动三者的联系[10]。Hernando(2008)建立了一个内生增长模型涉及要素节约型和技术进步，研究发现资本充裕的国家的可再生要素的投入比重将随着产出的增加而增加，而且更倾向于使用资本密集型的技术[11]。进一步地，在创新数量和质量较高的情况下，对要素投入应该具有一定的替代作用，而如果创新数量和质量不高时，创新数量和质量对要素投入可能会产生互补作用。当然这个问题比较复杂，比如高技术产业如果出现一些革命性的技术进步，也会催生新的要素投入。

2 研究方法与数据

2.1 基本方程与面板数据模型

第一步，根据经典的Cobb-Douglus生产函数，来建立高技术产业的生产函数：

log(Y)=c+α1log(K)+α2log(L)

(1)

在式(1)中，α1表示资本的弹性系数、α2表示劳动力的弹性系数，L、K、Y分别表示劳动力投入、资本投入、高技术产业效益，c为常数项。在此函数的基础上，增加创新数量R1、创新质量R2变量，同时考虑到创新数量与创新质量的共同作用，得：

log(Y)=c+α1log(K)+α2log(L)+α3log(R1)+α4log(R2)+α5log(R1)log(R2)

(2)

研究一般可以采用时序数据、截面数据或面板数据，考虑到我国高技术产业自有统计数据的时间不够长，而省际截面数据代表性差，数据较少，本文选择面板数据模型进行研究。Mundlak(1961)创立了面板数据模型，由于有足够多的数据数量，从而能够有效降低多重共线性的影响，其中的固定效应模型对于遗失重要变量不敏感，从而有效地提高估计效果[12]。

此外，由于高技术产业资本、劳动力、创新数量、创新质量与效益之间通常存在互动关系，也意味着存在变量的内生性问题，此时一般传统的估计方法就会失效，需要引入工具变量消除变量内生性的影响。本文选择解决此问题时最常用的SYS-GMM法来进行估计，这一方法由Blundell等(1998)提出，它不需要知道随机误差项的数据分布信息，允许序列和异方差相关，克服了差分广义矩法估计量较易受弱工具变量影响的不足，因此估计结果比其他参数估计方法更有效[13]。

2.2 贝叶斯向量自回归模型

贝叶斯向量自回归模型(BVAR)由Litterman(1986)创立，是在传统VAR模型基础上发展起来的一种优秀模型，其理论基础是贝叶斯推断理论(Bayesian Inference)，特点是不需要确定系数的精确数量关系，只要给定系数的分布函数，将围绕其均值波动的随机变量当作所有变量的系数[14]。系数随机变量包含预测者在预测前所获取的某些相关信息的某种可能的先验分布，Litterman分布也被称为Minnesota分布，是BVAR模型采用的先验分布。BVAR模型不会产生传统向量自回归方法的不可信结构，在短期预测时预测精度较高，因此得到了广泛的使用。

2.3 变量与数据

高技术产业投入产出生产函数中，用利润来表示高技术企业效益，用资产总计表示高技术企业资本，用从业人员平均人数表示高技术企业劳动力，根据Griliches(1990)的研究，用新产品销售收入表示高技术产业的创新数量，因为它反映了高技术产业创新的市场价值[15]。关于创新质量变量的选取，现有的方法较多，Lerner(1994)采用专利的IPC分类号数量的前4位数表示创新质量，并对其有效性进行验证[16]。张古鹏、陈向东和杜华东(2011)在研究中国地区间创新质量的差异时采用专利授权率和专利长度[17]。由于从产业角度相关数据无法获取，因此本文创新质量采用发明专利授权数与专利申请数的比例表示。

从2011年开始，资产总计数据才在《中国高技术产业统计年鉴》公布，因此本文从2011—2017年年鉴中选取相关数据。西藏地区数据缺失较多，故舍弃该地区数据，表1是变量的描述统计。

表1 变量描述统计

3 实证结果

3.1 变量的平稳性检验

首先对面板数据进行平稳性检验，以防止伪回归问题的出现。本文同时进行Hadri、LLC和ADF检验，以结果一致为准，发现经过一阶差分，所有的变量都是平稳时间序列。

3.2 创新数量与质量的弹性估计

接下来采用面板数据模型，在式(2)基础上，对创新数量、创新质量以及两者共同作用对高技术产业效益的作用进行估计。基于GMM模型进行估计，工具变量采用所有自变量的一阶滞后项。首先进行随机效应模型的估计，接下来进行Hausman检验，结果显示拒绝随机效应的原假设，选择固定效应模型进行估计。但创新数量与创新质量的共同作用没有通过统计检验，将其删除，结果见表2，其中为便于比较，表2同时给出混合回归结果。

表2 面板数据估计结果

从估计结果看，模型的拟合优度较高，R2高达0.989，对比混合回归的估计结果，所有变量弹性系数的排序一致，说明研究结果是稳健的。最高的是资本，弹性系数为0.497；第二是劳动力，弹性系数为0.271；接着是创新数量，弹性系数为0.104；但创新质量的弹性系数为-0.362。说明创新质量还不足以给高技术产业带来效益，本质上这和我国高技术产业创新水平不高有关，这样假设H1和假设H2均得到验证。

3.3 贝叶斯向量自回归模型估计

由于面板数据经过一阶差分后平稳，因此在此基础上可以建立BVAR模型，并对各要素的脉冲响应函数进行进一步分析。

高技术企业效益的脉冲响应函数见图2。资产总计和劳动力的正向冲击对企业效益的影响为正，又以资本的影响更为显著，这和面板数据模型中资本弹性系数大于劳动力是一致的。而无论是创新数量还是创新质量的正向冲击对企业效益的影响均为负，并且这种影响是长期的，说明高技术产业的创新是长期持续的过程，并且有其自身的规律，短期内的创新冲击对企业效益并没有好的促进作用。

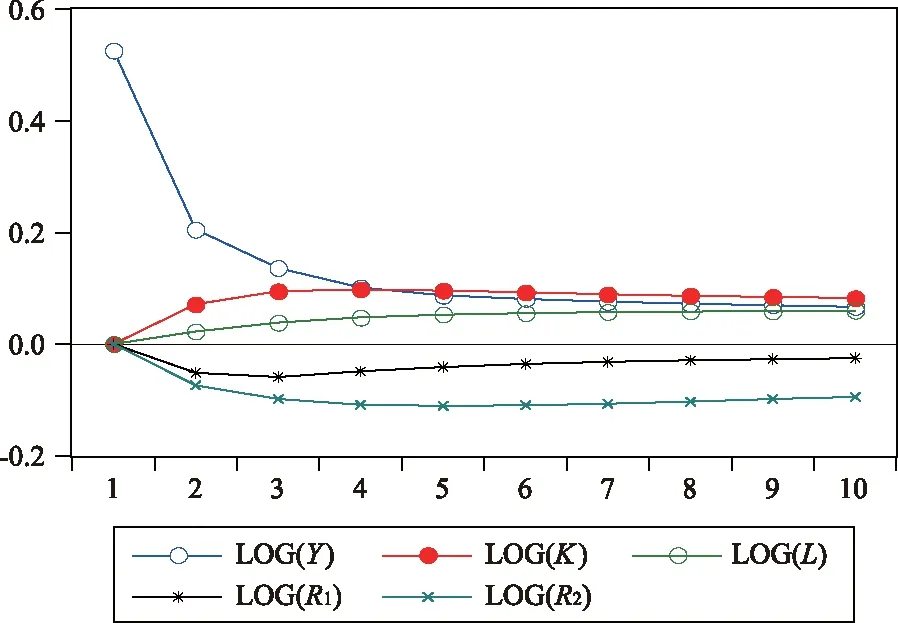
图2 企业效益的脉冲响应函数

图3为创新数量的脉冲响应函数。资产总计的冲击最大，当期就发生作用并且达到极大值；其次是劳动力的冲击，总体比较平稳，企业效益的冲击也具有正向影响。说明企业的规模与效益决定了企业必须保证一定规模的创新数量，但创新质量的冲击总体为负数，影响较小，这是因为企业研发投入是有限的，在保证数量的前提下要提高质量很难。

图3 创新数量的脉冲响应函数

图4为创新质量的脉冲响应函数。创新数量的冲击对其影响最大，总体作用比较平稳，说明只有在保证一定创新数量的基础上才能提高创新质量。资本的冲击具有短期正向影响，并且在当期达到极大值，说明企业投资和规模在扩大时已经注重创新质量的提高。劳动力的冲击对创新质量的影响短期为负，长期具有正向影响，而企业效益的冲击对创新质量的影响为负，说明企业效益提升后，往往不注重创新质量的提高。

图4 创新质量的脉冲响应函数

4 研究结论

创新数量与企业效益之间总体上呈良性互动关系。高技术产业创新数量对企业效益的弹性系数为正数，并且脉冲响应函数中，企业效益的冲击对创新数量具有正向反馈作用。但是高技术产业创新数量对企业效益的冲击为负，这是由高技术产业创新的特点决定的，高技术产业本身就是高风险产业，创新投入大，见效慢，时间长，加上我国高技术产业自有技术水平还不高，短期加大创新数量不仅增加大量的研发投入，并且往往难以取得较好的效益。

创新质量对企业效益的影响为负。创新质量对企业效益的弹性系数为负数，这和我国高技术产业创新质量较低有关。此外，从脉冲响应函数中可以看出，高技术产业创新质量的冲击对效益的影响为负，高技术企业效益的冲击对创新质量的影响也为负，两者并没有形成良性互动关系。这和我国创新中，发明专利占所有专利的比重较低，发明专利授权数占申请数的比重较低有关，根本原因是我国高技术产业创新质量较低。

创新数量是创新质量的基础。脉冲响应函数表明，高技术产业创新数量的正向冲击对创新质量具有正向影响，而创新质量的冲击对创新数量总体上呈现负面影响，这是因为提高创新质量必然要增加研发投入，在研发资源有限的情况下必然会影响到创新数量。而创新数量就不同了，只有保有一定规模的创新数量，才有可能产生一些高质量的创新。

创新数量和质量对资本呈现替代关系，对劳动力呈现互补关系。脉冲响应函数的结果表明，无论是创新数量还是创新质量的正向冲击，对资本呈现负面影响，即创新数量与质量的提升，可以减少资本的投入；对劳动力呈现正向影响，即可以带动就业。总体上，这是和我国高技术产业创新总量不够、创新水平不高有关，短期能够推动就业，有助于社会稳定，但长期应该尽快改善。