功能梯度圆柱壳的弹塑性屈曲

2021-11-02张靖华

兰州理工大学学报 2021年5期

张靖华, 郑武

(兰州理工大学理学院, 甘肃兰州 730050)

圆柱壳由于其出色的力学性能在工程中广受欢迎，再加上功能梯度材料可有效降低热应力集中、力学性能具有可设计性[1-2]，所以功能梯度材料圆柱壳的力学特性受到国内外研究者的广泛关注，尤其薄壁结构不可避免的稳定性问题已有很多研究成果.

结构的稳定性一直都是固体力学领域研究的重要内容，通常经历由静载到动载、由弹性到塑性的研究历程.针对FGM圆柱壳的弹性静态稳定性，Sun等[3-4]基于Hamilton原理，使用辛方法分别研究了热机耦合载荷作用下功能梯度圆柱壳的屈曲特性和考虑温度依赖时扭转载荷作用下FGM圆柱壳的屈曲特性，表明边界条件、体积分数指数、梯度材料特性和温升分布对屈曲行为有显著影响.Shen和Noda[5]对热环境中受轴向和径向复合载荷作用下有限长剪切变形功能梯度圆柱壳的后屈曲问题进行了分析.结果表明，温度场和体积分数对FGM壳体的后屈曲性能有显著影响，但对FGM壳体在复合加载条件下的缺陷敏感性影响较小.Pham等[6]采用解析法研究了功能梯度涂层圆柱壳的热-机屈曲和后屈曲行为，数值算例表明外弦对壳体的热机械屈曲和后屈曲行为有较大的影响.Amir和Soheil[7]在扩展有限元法的框架下，采用八节点退化壳单元对含裂纹的功能梯度圆柱壳进行特征值屈曲分析，并研究了裂纹长度、角度、材料梯度指数、圆柱壳长宽比、内压等参数对特征值屈曲的影响.

工程结构常常会受随时间变化的机械或热载荷作用.当结构受到动载荷时，对其稳定性分析静态理论已不适用，必须从更复杂更深入的动力学观点出发，研究其动力稳定性问题.对于FGM圆柱壳的弹性动态屈曲问题，Gao等[8]解决了正交各向异性FGM圆柱壳在纵向等速作用下的非线性动力屈曲，证实不同速度、初始缺陷、阻尼比、非均匀参数对FGM圆柱壳非线性动力屈曲行为都有影响.Bich等[9]研究了偏心FGM圆柱壳非线性动力屈曲问题.Mirzavand[10]研究了表面粘结压电作动器的功能梯度圆柱壳在热载荷和外加作动器电压共同作用下的动态热后屈曲行为.Zhang等[11]研究了热冲击载荷下功能梯度圆柱壳的弹性动力屈曲问题.Shariyat[12-13]分析了受热冲击、轴压和外压联合作用时FGM圆柱壳的复杂屈曲和在复杂的热-电-机组合载荷作用下，集成表面粘贴传感器和作动器层的非理想梯度材料圆柱壳的动态屈曲问题.结果说明体积分数指数、温度梯度、层序和自适应反馈控制对屈曲载荷有一定的影响.

以上研究仅限于FGM圆柱壳的弹性屈曲.若结构厚度尺寸较大，内部应力也较大，同时由于作为FGM重要组分的金属是塑性材料，它的存在极易使结构在应力较大的区域产生塑性变形，发生弹塑性屈曲破坏.目前关于FGM圆柱壳弹塑性屈曲问题的研究成果较少，Zhang等[14]研究了具有径向压力的梯度材料圆柱壳在轴压作用下的弹塑性屈曲行为.Huang和Han[15]基于Donnell理论和功能梯度材料J2流动本构关系，研究了功能梯度材料圆柱壳在轴压作用下的弹塑性屈曲行为，并研究了材料非线性、尺寸参数和幂律指数对屈曲的影响.Huang等[16]用半逆解法分析了FGM圆柱壳在扭转载荷作用下的屈曲行为，揭示了功能梯度材料的组成分布、尺寸参数和弹塑性材料特性对屈曲行为的影响.Xu等[17]研究了弹塑性功能梯度圆柱壳的屈曲后变形和应变变化历程，讨论了壳体厚度和组成分布对后屈曲行为的影响.在Hamilton体系下研究FGM圆柱壳的轴压弹塑性屈曲尚未见文献报道，本文将基于线性混合强化弹塑性模型，用辛求解方法求静力轴向压缩作用下功能梯度圆柱壳的临界载荷以及塑性流动区域，并分析了材料梯度指数，几何尺寸对于临界载荷及塑性流动区域的影响.

1 问题描述及解析分析

考虑FGM圆柱壳，长为l，壳体中曲面到中轴线的距离R，厚度为h，如图1所示，右端承受轴向静态压力N.并建立如图所示坐标原点位于左侧中轴线上的柱坐标系.

图1 功能梯度圆柱壳示意图Fig.1 Schematic diagram of the FGM cylindrical shells

1.1 材料特性描述

功能梯度材料通常由金属和陶瓷制成，假设陶瓷组分的体积分数满足幂函数分布特征，陶瓷相和金属相体积分数分别用Vc和Vm表示，其满足以下关系：

(1)

基于混合强化弹塑性模型，功能梯度圆柱壳的弹性模量E(z)、屈服极限σY(z)、强化模量H(z)如下：

式中:Em、Hm、Vm、σYm分别代表金属的弹性模量、强化模量、体积分数和屈服极限，Ec和Vc分别代表陶瓷的弹性模量和体积分数，q=0.045Ec.材料泊松比取为μ=0.3.

1.2 基本方程

根据经典壳理论，壳体上任一点的应变为[9]

(5)

式中：κx、κθ分别是x方向和θ方向的曲率，中曲面上应变与位移之间的关系为[15]

(6)

双向应力状态下的本构关系[11]：

(7a)

(7b)

1.3 正则方程

当圆柱壳屈曲时，在该静态机械加载作用下单位长度应变能表示为

(8)

(9)

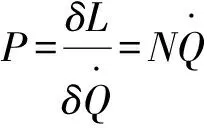
(10)

根据Hamilton原理，可得到对偶正则方程：

(11)

(12)

Q=C1eλ1X+C2eλ2X+C3eλ3X+C4eλ4X

(13)

式中：C1、C2、C3、C4为待定系数，λi(i=1,2,3,4)为特征方程Jλ4+ηλ2+ξ=0的四个根，

1.4 分叉条件

(14)

方程(14)有非零解，此时系数行列式为0，即

(15)

1.5 屈服条件

根据Mises屈服条件，当结构的等效应力σi达到屈服极限的时候，材料发生塑性变形.即

σY-σi=0

(16)

对处于双向应力状态下的FGM圆柱壳，等效应力可表示为

(17)

基于截面等应变假设，即圆柱壳发生屈曲时的临界状态下，横截面上的各点应变相同，满足以下表达式：

(18)

联立式(1,16～18)可求得弹塑性分界面位置s:

(19)

为了更清楚地分析圆柱壳弹塑性屈曲的分界面位置随圆柱壳厚度的变化情况，本文引入相对弹塑性界面：

(20)

2 数据计算与结果分析

本文将材料参数及方程通过Maple软件编程进行数值计算.数值求得FGM圆柱壳的刚度系数和弹塑性分界面s，代入分叉条件式(15)中，此时式(15)变成一个含有未知数N的超越方程，利用Newton-Raphson法数值求出相应的无量纲临界载荷Ncr.

本文在具体数值计算时选脆性陶瓷材料为ZrO2，其只发生弹性变形；塑性金属材料为Ti-6Al-4V，其可发生塑性变形，它们的弹塑性物性参数可见文献 [2].并将计算得数值结果以图线形式展示出来.图2为R/h=10、R/h=12以及R/h=14的圆柱壳，弹塑性界面s随n的变化曲线.从计算中可以发现，当n比较小的时候，即对本文所选取的功能梯度材料，由于n过小，导致陶瓷组分很大，而发生塑性屈曲依赖于金属组分，故当n过小的时候，即n<3的时候，FGM圆柱壳不会发生弹塑性屈曲，只会发生弹性屈曲.随着n的增大，陶瓷组分越来越小，金属组分越来越大，从图中可以看出，弹塑性界面的数值会变小，即塑性流动面由金属面向陶瓷面靠近.随着梯度指数变大，金属组分越来越大，故功能梯度材料越来越易于发生塑性屈曲，因此塑性区域越来越大，最初在金属面发生塑性变形，所以弹塑性界面由金属面向陶瓷面靠近，塑性流动区增大.随着梯度指数越来越大，弹塑性界面的位置变化越来越平缓，这是由于采用幂函数表示材料组分，当梯度指数到一定值，功能梯度材料趋近于纯金属材料，故弹塑性界面变化趋于平缓.

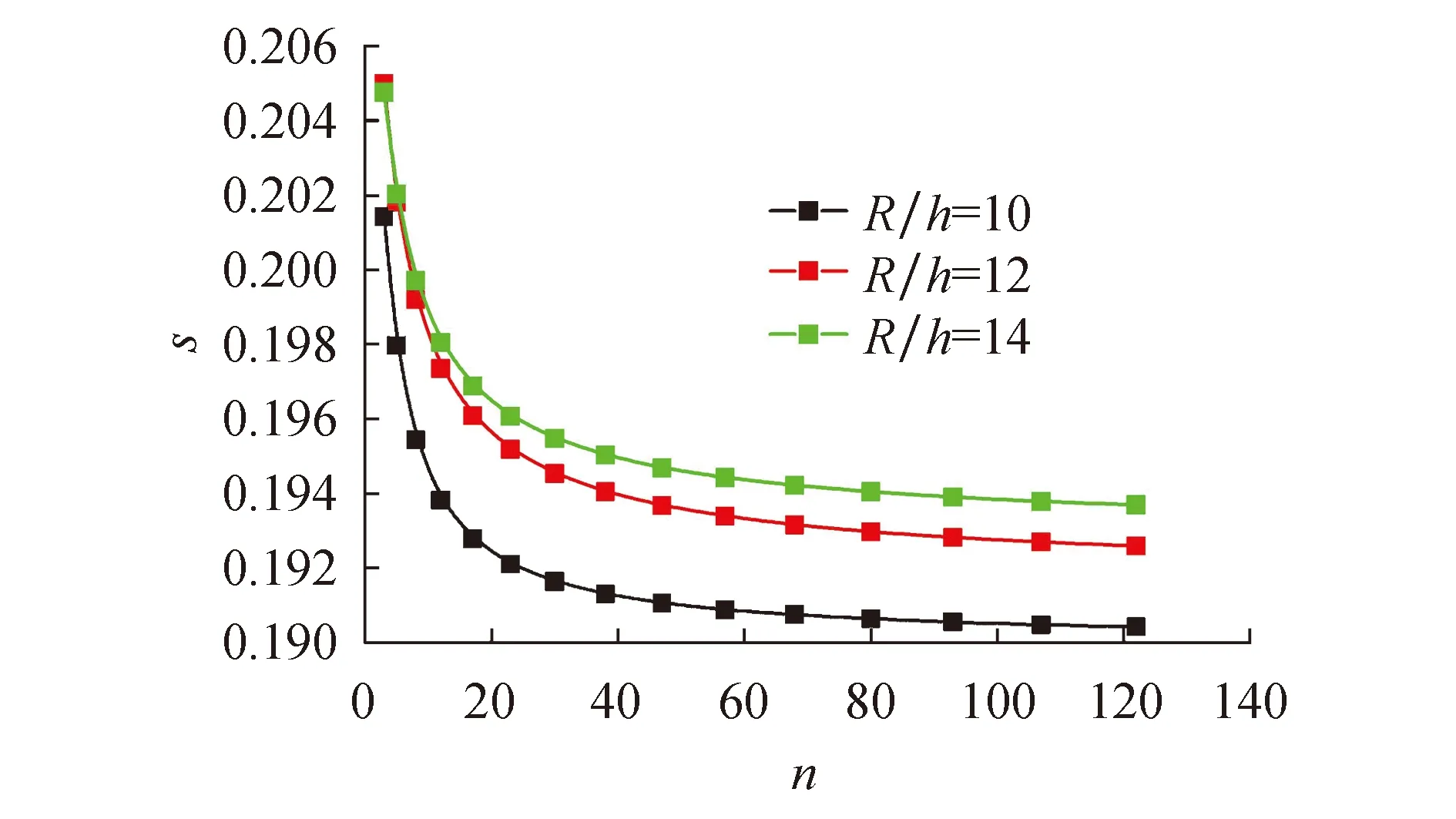
图2 弹塑性界面s随梯度指数n的变化Fig.2 The elastoplastic interface s versus power law index n

图3为R/h=10、R/h=12以及R/h=14的圆柱壳，相对弹塑性界面S随n的变化曲线.分析图3可以发现当壳体的R/h一定时，相对弹塑性界面的数值同样随着n的增大而减小，该趋势与图2相同.由图3可知，当梯度指数n一定时，即同种功能梯度材料，壳体越薄，相对弹塑性界面越靠近金属面.这是由于壳体越薄，发生弹塑性屈曲时的临界载荷越小，故相对塑性区域越小，从而导致相对弹塑性界面更靠近金属侧.

图3 相对弹塑性界面S随梯度指数n的变化Fig.3 The relatively elastoplastic interface S versus power law index n

图4描绘了R/h=10、R/h=12以及R/h=14的圆柱壳，弹塑性临界载荷Ncr随梯度指数n的变化关系曲线.分别从图4的三条曲线可以看出，FGM圆柱壳的临界载荷随着n的增大逐渐变小，是由于n的增大，陶瓷组分逐渐减小，金属组分增大，发生弹塑性屈曲取决于金属组分.金属组分越大，整体的刚度减小，越易发生弹塑性屈曲，所以临界载荷也逐渐减小.从图中可以直观地看出，当n增大到一定值，即n>40时临界载荷趋于常量，这是由于当n较大时，FGM圆柱壳已经非常趋近于金属圆柱壳了，材料参数几乎没有变化，故临界载荷也几乎不变.根据该变化特性，调节功能梯度指数n可以控制FGM圆柱壳的临界载荷，因此可根据实际工程需要，通过调节梯度指数n制造出满足条件的FGM结构.当n一定时，即同种FGM圆柱壳，R/h越大则临界载荷越小，R/h越大意味着圆柱壳

图4 临界载荷Ncr随梯度指数n的变化

越薄，越薄的圆柱壳则更易发生弹塑性屈曲，反之则更难.基于此，可根据工程需要，通过调整R/h的大小对FGM结构进行优化设计.

表1～表3分别列出了圆柱壳长度为l=R、l=1.5R、l=2R时不同梯度指数功能梯度圆柱壳的临界载荷Ncr.通过对比这三张表可以发现，当n和R/h一定时l=R的圆柱壳临界载荷最大，l=2R的临界载荷最小，即同种且横截面积相同的FGM圆柱壳，长度越长则临界载荷越小，这是因为结构整体刚度随长度的增大而减小的缘故.