基于灰色理论的数控机床复合结构床身优化设计及其性能分析
2021-11-02郭润兰邓文强李典伦
郭润兰, 邓文强, 李典伦
(兰州理工大学 机电工程学院, 甘肃 兰州 730050)
随着制造业的飞速发展,现有的机床越来越难满足高速高精的加工要求.作为机床基础件,床身结构的强度、刚度和稳定性对机床加工精度有重要影响.为满足新的加工要求,需要尽量提高床身的静态、动态刚度和热性能[1].
近年来,国内外学者为提高机床的综合性能作了大量的研究与尝试,形成的方法包括优化机床结构和应用新材料、新结构制造机床两种[2].应申舜等[3]采用模态验证法对某拉床床台进行了优化,陈永亮等[4]采用Kriging代理模型对某高速铣床主轴箱进行了优化,刘成颖等[5]采用元结构二次优化方法对某卧式加工中心的床身进行了优化,徐平等[6]提出用钢纤维树脂混凝土制造机床基础件,任秀华等[7]提出用钼纤维树脂矿物复合材料制造机床床身,Kono等[8]提出用钢和碳纤维增强塑料复合材料来制造机床主轴.
优化机床结构的技术相对成熟,得到了广泛的应用,但较难从根本上改善机床的性能,现阶段取得的效果几乎接近极限[9].因此,应用新材料、新结构制造机床逐渐成为了研究的热点.现有研究[10-11]表明,采用钢板-混凝土复合结构制造机床基础件是一种可行的方法,但这种结构在应用上缺乏明确的设计依据,制造的机床基础件无法获得满意的性能.因此,本文设计了一种钢-混凝土复合结构床身,并通过正交实验、灰色关联、组合赋权方法对床身的结构参数进行多目标优化,从而提高机床床身的综合性能.
1 复合结构床身静力学分析
1.1 复合结构床身设计
本文参照的HMC630卧式加工中心,其结构模型如图1a所示.根据该卧式加工中心铸铁床身,在不改变床身关键尺寸、结构及功能完整性的前提下,利用钢板-混凝土复合结构对其进行重新设计.床身外层用45号钢焊接,内部分布加强钢筋并用C30混凝土填实,机床导轨底部埋入混凝土并与外层钢板连接.该床身初定钢板厚度t=11 mm,导轨预埋深度h=45 mm,其局部结构如图1b所示.

图1 HMC630卧式加工中心结构模型和床身内部结构示意图Fig.1 Structure model of HMC630 horizontal MC Schematic diagram of the internal structure of the machine tool bed
1.2 工况分析及参数计算
选取典型工况,研究该卧式加工中心床身的受力情况.查表得其铣削力经验公式如下:
式中:cp为工件材料对铣削力的影响系数;ap为铣削深度;fz为每齿进给量;d0为铣刀直径;K为刀具前角对铣削力的影响系数;K1为铣削速度对铣削力的影响系数;Ft为横向铣削分力;Ff为纵向铣削分力;Fv为垂直铣削分力.
最后求得:Fc=2 064 N,Ft=774 N,Ff=1 755 N,Fv=1 600 N.x轴导轨上表面和侧面所受载荷为F1=27100N,T1=310 N·m;z轴导轨上表面和侧面所受载荷为F2=15 600 N,T2=702 N·m.
1.3 复合结构床身静力学分析
分析时对模型作适当简化,忽略混凝土与钢板结合部参数对有限元结果的影响.45号钢的密度为7 850 kg/m3,泊松比为0.30,弹性模量200 GPa,阻尼比为0.004,比热容为434 J/(kg·℃),导热系数为60.5 W/(m·℃),线膨胀系数为1.2×10-5K-1;C30混凝土的密度为2 300 kg/m3,泊松比为0.18,弹性模量30 GPa,阻尼比为0.015,比热容为780 J/(kg·℃),导热系数为0.72 W/(m·℃),线膨胀系数为1.4×10-5K-1.
床身静力学分析结果如图2所示.由图可知,复合结构床身最大静应力为1.738 9 MPa,发生在地脚螺栓安装模块上;最大静变形为2.371 1 μm,发生在机床z轴导轨上.
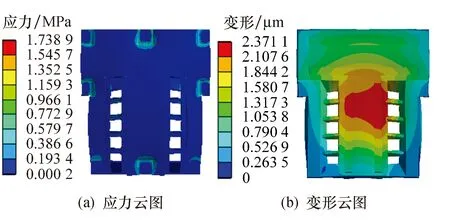
图2 应力云图和变形云图Fig.2 Stress and deformed cloud diagram
2 复合结构床身多目标优化设计
2.1 优化设计方法及流程
本文采用正交实验、灰色关联和组合赋权相结合的方法对该复合结构床身进行多目标优化.具体优化流程如图3所示.
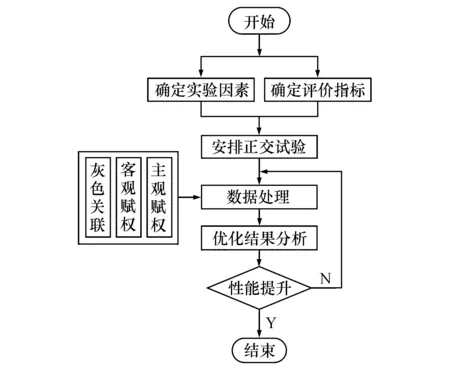
图3 优化设计流程Fig.3 Process of optimal design
2.2 实验因素和评价指标的确定
选取外层钢板厚度、导轨预埋深度和加强钢筋结构作为实验因素,选取最大静应力、最大静变形、一阶固有频率和质量作为评价指标,对复合结构床身进行多目标优化设计.本文设计了如图4所示的4种加强钢筋结构来研究其对床身性能的影响,其中钢筋结构③为初始设计.

图4 床身加强钢筋结构布置方案Fig.4 Scheme of reinforcing steel structure inside the machine tool bed
2.3 正交实验设计
各实验因素在合适范围内选取4个水平,设计了如表1所列的L16(43)正交实验,各实验方案的有限元仿真结果如表2所列.
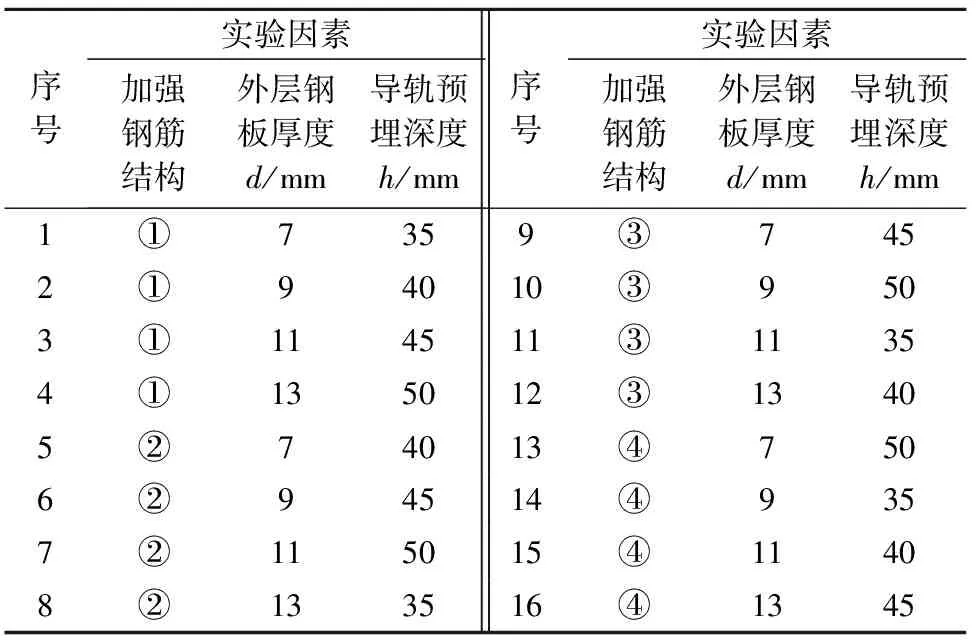
表1 正交实验设计Tab.1 Orthogonal experimental design

表2 仿真实验结果Tab.2 Simulation experimental results
2.4 基于灰色系统理论的数据处理
本文对复合结构床身进行了16次仿真实验,而实际的参数组合有64种,这构成了一个小样本、数据匮乏的不确定性系统[12].灰色关联法是根据因素之间发展趋势的相同或差异程度来评价因素间关联度的方法,恰好能够解决这种不确定性系统的多目标优化设计问题[13].
2.4.1灰色关联法
根据灰色关联法,以实验方案的仿真数据建立评价指标的初始矩阵,并对初始初始矩阵进行无量纲、规范化处理后得到矩阵
(5)
构造参考矩阵K=[k1,k2,k3,k4],kj=max(a1,j,a2,j,…,a16,j),记ξij为第i个比较序列与K中第j个指标的关联系数,即
(6)
式中:i=1, 2,…,16;j=1,2,3,4;ρ为分辨系数,一般取ρ=0.5.
由式(6)处理后得到关联系数矩阵
(7)
2.4.2组合赋权法
本文采用基于熵值法和层次分析法的组合赋权法对已有数据进行处理,步骤如下:
计算第j项指标下第i个数据的比重
(8)
计算第j项指标的熵值
(9)
计算客观权重w′j
(10)
按照层次分析法确定主观权重w″j后,对主、客观权重进行组合,组合权重为
(11)
2.4.3计算各实验方案关联系数
γ=ζw
(12)
式中:w为wj(j=1,2,3,4)组成的组合权重系数矩阵,γ为目标函数灰色关联度矩阵.
2.5 最优参数组合的确定
由式(8~11)得到各优化目标的组合权重w′=[0.264 8,0.510 9,0.123 4,0.1009].
由式(5~12)得到各实验方案的灰色关联度,如表3所列.由表3得到各因素水平的平均灰色关联度,如表4所列.由表4可知,复合结构床身的最优参数组合为:加强钢筋结构②,外层钢板厚度d=13 mm,导轨预埋深度h=50 mm.

表3 各实验灰色关联度Tab.3 Gray correlation degree of each experiment

表4 各因素水平的平均关联度Tab.4 Average correlation of each factor level
为验证优化效果,对优化后复合结构床身进行有限元仿真,结果如表5所列.由表5可知,相比优化前,复合结构床身的质量增加了2.7%,最大静应力和最大静变形分别下降了18.7%和11.0%,一阶固有频率提高了3.1%.
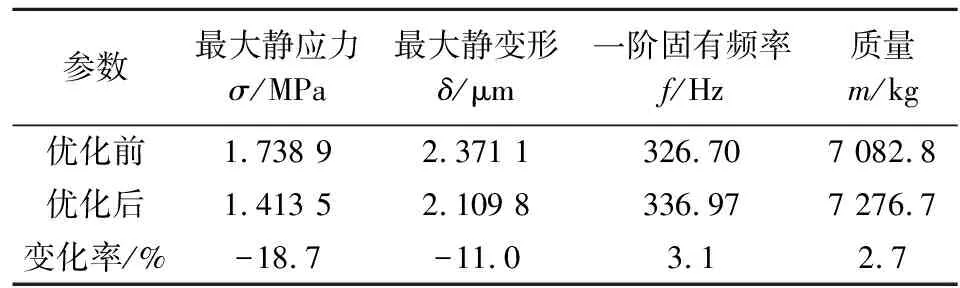
表5 复合结构床身优化前后有限元分析结果Tab.5 Finite element analysis results of composite structure bed before and after optimization
由组合权重w可知,最大静应力、最大静变形、一阶固有频率和质量的组合权重分别为0.264 8、0.510 9、0.123 4和0.100 9.优化时应重点考虑降低床身的变形和应力,然后考虑减少床身质量.因此,在其他3项指标得到较好优化后,床身质量反而有小幅增加.这是由各优化目标的组合权重w所决定的.综上所述,优化结果达到了预期目标,优化效果较好.
3 优化后复合结构床身性能分析
3.1 静力学分析及模态分析
分析时,复合结构床身材料参数设置同1.3节的内容,铸铁的密度为7 200 kg/m3,泊松比为0.28,弹性模量110×109Pa,阻尼比为0.006,比热容为447 J/(kg·℃),导热系数为52 W/(m·℃),线膨胀系数为1.2×10-5K-1.
有限元分析结果如表6所列.由表6可知,相比原型铸铁床身,复合结构床身质量有小幅增加,但其最大静应力和最大静变形都有了大幅降低,前三阶固有频率也得到了明显提高.

表6 复合结构床身与原型铸铁床身性能Tab.6 Performance between composite structure machine tool bed and prototype cast iron machine tool bed
3.2 谐响应分析
分析时,取机床x轴和z轴导轨中心节点为研究对象,设置的频率范围包含两种结构床身的前三阶固有频率.复合结构床身的阻尼比由钢和混凝土对整体刚度的贡献率确定[14],查阅相关标准[15],最后确定复合结构床身的阻尼比取0.03,原型铸铁床身的阻尼比取0.006.
谐响应分析结果如图5所示.由图5可知,原型铸铁床身x轴和z轴导轨中心节点x、y、z方向的最大振幅为4.13、540.91、381.47μm和164.57、953.72、65.18μm;复合结构床身x轴和z轴导轨中心节点x、y、z方向的最大振幅为0.10、15.79、22.70 μm和0.59、20.19、9.52 μm;相比原型铸铁床身,复合结构床身x轴和z轴导轨中心节点x、y、z方向的最大振幅分别降低了97.6%、97.1%、94.0%和99.6%、97.9%、85.4%.

图5 床身导轨中心节点频响曲线
3.3 热态性能分析
3.3.1热源分析计算
本文主要考虑工作台与z轴导轨、立柱与x轴导轨的摩擦生热以及环境温度对床身的影响.导轨热流密度的计算公式为
(13)
式中:μ为摩擦系数,取0.075;F为导轨摩擦面所受的载荷,N;v为导轨滑块的移动速度;J为热功当量,J=4.2 J/cal;S为导轨摩擦表面积,mm2.
本文参照的HMC630卧式加工中心,其允许的最大线性移动速度为18 m/min,计算时取最大值v=0.3 m/s.
x轴导轨表面的热流密度
z轴导轨表面的热流密度
根据努谢尔特准则、普朗特准则和葛拉晓夫准则计算床身各表面对流换热系数,结果如表7所示.

表7 对流换热系数Tab.7 Convective heat transfer coefficient
3.3.2热及热-结构耦合分析
在0~3 600 s内取样15个时间点,对复合结构床身和原型铸铁床身导轨的热及热-结构耦合性能进行有限元仿真.分析时,床身初始温度和环境温度均设为22 ℃.
Fig.5 Frequency response curve of the center node of the
machine tool bed rail
本文采用顺序耦合的方式进行两种结构床身的热-结构耦合性能分析,复合结构床身和原型铸铁床身导轨的时间-最高温度曲线和时间-最大耦合变形曲线分别如图6所示.由图6可知,0~1 920 s,铸铁床身导轨的最高温度略高于复合结构床身的;1 920~3 600 s,复合结构床身导轨的最高温度略高于原型铸铁床身的;0~3 600 s,复合结构床身导轨的最大热-结构耦合变形量均小于铸铁床身的.

图6 时间与最高温度和最大耦合变形的曲线Fig.6 Time maximum temperature and maximum coupling deformation curve
受实际工况影响,该卧式加工中心单个工序的加工时间基本上不超过1 200 s,在此时间范围内,复合结构床身导轨的最高温度和最大耦合变形量均低于铸铁床身的.1 920 s后,虽然复合结构床身导轨的最高温度略高于铸铁床身的,但是其最大耦合变形量始终低于铸铁床身的.因此,该复合结构床身的热性能要优于原型铸铁床身的.
4 结论
1) 以某卧式加工中心铸铁床身为原型,设计了一种钢板-混凝土复合结构床身,研究了该复合结构床身的静力学性能,分析出其最大静应力和最大静变形的大小和发生位置.
2) 采用正交实验方法,综合考虑主、客观赋权对评价结果的影响,利用灰色关联法得到床身的最优参数组合,有效地减少了实验次数.
3) 对优化后的复合结构床身进行了有限元仿真分析,并将结果与原型铸铁床身比较.结果表明:在床身质量仅增加2.3%的情况下,复合结构床身的最大静应力和最大静变形降低了51.3%和82.9%;前三阶固有频率提高了143.9%、156.8%和148.7%,x轴和z轴导轨中心节点x、y、z方向上的最大振幅分别降低了97.6%、97.1%、94.0%和99.6%、97.9%、85.4%;0~3 600 s,复合结构床身的最大热-结构耦合变形均小于原型铸铁床身的.由此说明钢板-混凝土复合结构床身具有更好的静态、动态刚度和热稳定性.
